貝葉斯機(jī)器學(xué)習(xí)路線圖
本文轉(zhuǎn)自圖靈人工智能
貝葉斯統(tǒng)計是統(tǒng)計的一個分支,它的特點是把我們感興趣的量(比如統(tǒng)計模型的參數(shù))看作隨機(jī)變量. 給定觀察數(shù)據(jù)后, 我們對這些量的后驗分布進(jìn)行分析從而得出結(jié)論. 雖然貝葉斯統(tǒng)計的核心思想已經(jīng)歷經(jīng)很多年了, 但貝葉斯的思想在過去近20年對機(jī)器學(xué)習(xí)產(chǎn)生了重大影響, 因為它在對真實世界現(xiàn)象建立結(jié)構(gòu)化模型時提供了靈活性. 算法的進(jìn)步和日益增長的計算資源使得我們可以擬合豐富的, 高度結(jié)構(gòu)化的模型, 而這些模型在過去是很棘手的.
這個路線圖旨在給出貝葉斯機(jī)器學(xué)習(xí)中許多關(guān)鍵思想的指引. 如果您正考慮在某些問題中使用貝葉斯方法, 您需要學(xué)習(xí)"核心主題"中的所有內(nèi)容. 即使您只是希望使用諸如?BUGS,?Infer.NET, 或?Stan等軟件包, 這些背景知識也對您很有幫助. 如果這些軟件包不能馬上解決您的問題, 知道模型的大致思想可幫助您找出問題所在.
如果您正考慮研究貝葉斯機(jī)器學(xué)習(xí), 那么許多論文會假設(shè)您已經(jīng)掌握了核心主題的內(nèi)容以及部分進(jìn)階主題的內(nèi)容, 而不再給出參考文獻(xiàn). 閱讀本路線圖時, 我們不需要按順序?qū)W習(xí), 希望本文可以在您需要時為您提供幫助.
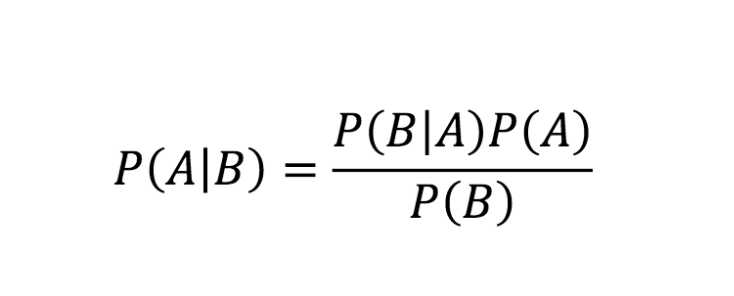
本文目錄結(jié)構(gòu)如下:
核心主題
貝葉斯信息準(zhǔn)則(Bayesian information criterion)
拉普拉斯近似(Laplace approximation)
混合高斯
因子分析
隱馬爾科夫模型(HMM)
MAP估計
Gibbs采樣
馬爾科夫鏈蒙特卡洛(MCMC)
變分推斷(Variational inference)
最大似然
正則化
EM算法
參數(shù)估計
模型比較
中心問題
非貝葉斯方法
基本推斷算法
模型
貝葉斯模型比較
進(jìn)階主題
無信息先驗(uninformative priors)
最大似然的漸進(jìn)(asymptotics of maximum likelihood)
Jeffreys prior
樹結(jié)構(gòu)圖模型
非樹結(jié)構(gòu)圖模型
Sum-product algorithm
Max-product algorithm
循環(huán)信念傳播(Loopy belief propagation)
連接樹算法(Junction tree algorithm)
變分貝葉斯(Variational Bayes)
平均場近似(Mean field approximation)
期望傳播(expectation propagation)
折疊Gibbs采樣(Collapsed Gibbs sampling)
哈密爾頓蒙特卡洛(Hamiltonian Monte Carlo)(HMC)
切片采樣(Slice sampling)
可逆跳躍MCMC(reversible jump MCMC)
Sequential Monte Carlo(SMC)
粒子濾波器(Particle filter)
退火重要性采樣(Annealed importance sampling)
高斯過程(Gaussian processes)
Chinese restaurant process(CRP)
Hierarchical Dirichlet process
Indian buffet process(IBP)
Dirichlet diffusion trees
Pitman-Yor process
邏輯回歸(Logistic regression)
貝葉斯網(wǎng)絡(luò)(Bayesian networks)
Latent Dirichlet allocation(LDA)
線性動態(tài)系統(tǒng)(Linear dynamical systems)
稀疏編碼(Sparse coding)
模型
貝葉斯非參數(shù)
采樣算法
變分推斷
信念傳播(Belief propagation)
核心主題
這一章覆蓋了貝葉斯機(jī)器學(xué)習(xí)的核心概念. 如果您希望使用這些工具, 建議您學(xué)習(xí)本章的所有內(nèi)容.
中心問題
什么是貝葉斯機(jī)器學(xué)習(xí)? 一般來說, 貝葉斯方法旨在解決下面給出的某一個問題:
參數(shù)估計(parameter estimation)
假設(shè)您已經(jīng)建好了一個統(tǒng)計模型, 并且希望用它來做預(yù)測. 抑或您認(rèn)為模型中的參數(shù)很有意義, 所以希望擬合這些參數(shù)來學(xué)習(xí)到某些東西. 貝葉斯方法是在給定觀察數(shù)據(jù)后, 去計算或者近似這些參數(shù)的后驗分布.
您通常會希望使用訓(xùn)練好的模型來作出一些決策行為.?貝葉斯決策理論(Bayesian decision theory)提供了選擇行為的一個框架.
模型比較(model comparison)
您可能有許多個不同的候選模型, 那么哪一個是最貼切給定數(shù)據(jù)的呢? 一種常見的情形是: 您有一些形式相同但復(fù)雜度不同的模型, 并且希望在復(fù)雜度和擬合度間權(quán)衡.
與選擇單個模型相比, 您可以先為模型定義先驗, 并且根據(jù)模型的后驗對預(yù)測進(jìn)行平均. 這便是貝葉斯模型平均(bayesian model averaging).
此外,?貝葉斯網(wǎng)絡(luò)(Bayesian networks)?(Bayes nets)的基礎(chǔ)知識也值得一學(xué), 因為這些符號在討論貝葉斯模型時會經(jīng)常用到. 由于貝葉斯方法把模型參數(shù)也看作隨機(jī)變量, 所以我們可以把貝葉斯推斷問題本身表達(dá)為貝葉斯網(wǎng)絡(luò).
閱讀本章內(nèi)容會告訴您貝葉斯方法解決什么問題, 但是沒告訴您一般情況下, 如何真正地解決這些問題. 這是本路線圖剩余部分將討論的內(nèi)容.
非貝葉斯方法(Non-Bayesian techniques)
作為背景知識, 了解如何使用非貝葉斯方法擬合生成模型是有助于理解的. 這么做的其中一個理由是: 這些方法更易于理解, 并且一般來說結(jié)果已經(jīng)足夠好了. 此外, 貝葉斯方法跟這些方法存在一些相似性, 學(xué)習(xí)這些方法后, 通過類比可以幫助我們學(xué)習(xí)貝葉斯方法.
最基礎(chǔ)的, 您需要明白?泛化(generalization)的符號, 或者知道一個機(jī)器學(xué)習(xí)算法在未知數(shù)據(jù)上表現(xiàn)如何. 這是衡量機(jī)器學(xué)習(xí)算法的基礎(chǔ). 您需要理解以下方法:
最大似然(maximum likelihood)
擬合模型參數(shù)的準(zhǔn)則.正則化(regularization)
防止過擬合的方法.EM算法(the EM algorithm)
為每個數(shù)據(jù)點都有與之相關(guān)聯(lián)的潛在變量(未觀測變量)的生成模型擬合參數(shù).
基本推斷算法
一般來說, 貝葉斯推斷需要回答的問題是: 給定觀察數(shù)據(jù)后, 推斷關(guān)于模型參數(shù)(或潛在變量(latent variables))的后驗分布. 對于一些簡單模型, 這些問題擁有解析解. 然而, 大多數(shù)時候, 我們得不到解析解, 所以需要計算近似解.
如果您需要實現(xiàn)自己的貝葉斯推斷算法, 以下可能是最簡單的選擇:
MAP估計(MAP estimation)
使用最優(yōu)參數(shù)的點估計來近似后驗. 這把積分問題替換為了優(yōu)化問題. 但這并不代表問題就很簡單了, 因為優(yōu)化問題本身也常常很棘手. 然而, 這通常會簡化問題, 因為優(yōu)化軟件包比采樣軟件包更普適(general)也更魯棒(robust).吉布斯采樣(Gibbs sampling)
吉布斯采樣是一種迭代的采樣過程, 每一個隨機(jī)變量都從給定其他隨機(jī)變量的條件分布中采樣得到. 采樣的結(jié)果很有希望是后驗分布中的一個近似樣本.
您還應(yīng)該知道下列常用的方法. 他們的一般公式大多數(shù)時候都過于寬泛而難以使用, 但是在很多特殊情形下, 他們還是很強(qiáng)大的
馬爾科夫鏈蒙特卡洛(Markov chain Monte Carlo)
一類基于采樣的算法, 這些算法基于參數(shù)的馬爾科夫鏈, 該馬爾科夫鏈的穩(wěn)態(tài)分布是后驗分布.
1.特別的,?Metropolis-Hastings?(M-H)算法是一類實用的構(gòu)建有效MCMC鏈的方法. 吉布斯采樣也是M-H算法的特例.變分推斷(Variational inference)
嘗試用易于處理的分布去近似難以處理的分布. 一般來說, 易處理分布的參數(shù)通過最小化某種度量指標(biāo)來選擇, 這個度量指標(biāo)衡量了近似分布和真實分布之間的距離.
模型
以下是一些簡單的生成模型, 這些模型常常運(yùn)用貝葉斯方法.
混合高斯(mixture of Gaussians)
混合高斯模型中, 每個數(shù)據(jù)點屬于若干簇或者群組中的其中一個, 每個簇中的數(shù)據(jù)點都服從高斯分布. 擬合這樣一個模型可以讓我們推斷出數(shù)據(jù)中有意義的分組情況.因子分析(factor analysis)
因子分析中, 每個數(shù)據(jù)點被更低維度的線性函數(shù)近似表達(dá). 我們的想法是, 潛在空間(latent space)中每個維度對應(yīng)一個有意義的因子, 或者數(shù)據(jù)中變化的維度.隱馬爾科夫模型(hidden Markov models)
隱馬爾科夫模型適用于時間序列數(shù)據(jù), 其中有一個潛在的離散狀態(tài)隨著時間的推移而演變.
雖然貝葉斯方法大多數(shù)時候與生成模型相聯(lián)系, 但它也可以被用于判別模型的情況. 這種情形下, 我們嘗試對已知觀測數(shù)據(jù)時目標(biāo)變量的條件分布直接進(jìn)行建模. 標(biāo)準(zhǔn)的例子是貝葉斯線性回歸(Bayesian linear regression).
貝葉斯模型比較
推斷算法的小節(jié)為我們提供了近似后驗推斷的工具. 那么比較模型的工具是什么呢? 不幸的是, 大多數(shù)模型比較算法相當(dāng)復(fù)雜, 在您熟悉下面描述的高級推理算法前, 您可能不想自己實現(xiàn)它們. 然而, 有兩個相當(dāng)粗略的近似模型比較是較為容易實現(xiàn)的.
貝葉斯信息準(zhǔn)則(Bayesian information criterion )(BIC)
貝葉斯信息準(zhǔn)則簡單地使用MAP解并添加一個罰項, 該罰項的大小正比于參數(shù)的數(shù)量.拉普拉斯近似(Laplace approximation)
使用均值與真實后驗分布MAP相同的高斯分布對后驗分布進(jìn)行近似.
進(jìn)階主題
本章將討論貝葉斯機(jī)器學(xué)習(xí)中更進(jìn)階的主題. 您可以以任何順序?qū)W習(xí)以下內(nèi)容
模型
在"核心主題"一章中, 我們列出了一些常用的生成模型. 但是大多數(shù)的數(shù)據(jù)集并不符合那樣的結(jié)構(gòu). 貝葉斯建模的強(qiáng)大之處在于其在處理不同類型的數(shù)據(jù)時提供了靈活性. 以下列出更多的模型, 模型列出的順序沒有特殊意義.
邏輯回歸(logistic regression)
邏輯回歸是一個判別模型, 給定輸入特征后, 對二元目標(biāo)變量進(jìn)行預(yù)測.貝葉斯網(wǎng)絡(luò)(Bayesian networks)?(Bayes nets).
概括地說, 貝葉斯網(wǎng)絡(luò)是表示不同隨機(jī)變量間概率依賴關(guān)系的有向圖, 它經(jīng)常被用于描述不同變量間的因果關(guān)系. 盡管貝葉斯網(wǎng)絡(luò)可以通過非貝葉斯方法學(xué)習(xí), 但貝葉斯方法可被用于學(xué)習(xí)網(wǎng)絡(luò)的?參數(shù)(parameters)?和?結(jié)構(gòu)(structure)(網(wǎng)絡(luò)中的邊)
線性高斯模型(Linear-Gaussian models)是網(wǎng)絡(luò)中的變量都服從聯(lián)合高斯的重要特殊情況. 即使在具有相同結(jié)構(gòu)的離散網(wǎng)絡(luò)難以處理的情況下, 這些網(wǎng)絡(luò)的推論都常易于處理.
latent Dirichlet allocation(LDA)
LDA模型是一個"主題模型", 其假定一組文檔(例如網(wǎng)頁)由一些主題組成, 比如計算機(jī)或運(yùn)動. 相關(guān)模型包括非負(fù)矩陣分解(nonnegative matrix factorization)和?概率潛在語義分析(probabilistic latent semantic analysis)線性動態(tài)系統(tǒng)(linear dynamical systems)
一個時間序列模型. 其中, 低維高斯?jié)撛跔顟B(tài)隨時間演變, 并且觀察結(jié)果是潛在狀態(tài)的噪聲線性函數(shù). 這可以被認(rèn)為是HMM的連續(xù)版本. 可以使用卡爾曼濾波器(Kalman filter)和平滑器(smoother)來精確地執(zhí)行該模型中的判斷.稀疏編碼(sparse coding)
稀疏編碼中每一個數(shù)據(jù)點被建模為從較大的字典中抽取的少量元素的線性組合. 當(dāng)該模型被應(yīng)用于自然圖像像素時, 學(xué)習(xí)的字典類似于主視覺皮層中的神經(jīng)元的接受字段. 此外, 另一個密切相關(guān)的模型稱為獨立成分分析(independent component analysis).
貝葉斯非參數(shù)
上述所有模型都是參數(shù)化的, 因為它們是以固定的有限數(shù)量的參數(shù)表示的. 這是有問題的, 因為這意味著我們需要預(yù)先指定一些參數(shù)(比如聚類中的簇的數(shù)目), 而這些參數(shù)往往是我們事先不知道的.
這個問題可能對上述模型看起來并無大礙, 因為對于諸如聚類的簡單模型, 我們通常可以使用交叉驗證來選擇好的參數(shù). 然而, 許多廣泛應(yīng)用的模型是更為復(fù)雜的, 其中涉及許多獨立的聚類問題, 簇的數(shù)量可能是少數(shù)幾個, 也可能是數(shù)千個.
貝葉斯非參數(shù)是機(jī)器學(xué)習(xí)和統(tǒng)計學(xué)中不斷研究的領(lǐng)域, 通過定義無限復(fù)雜的模型來解決這個問題. 當(dāng)然, 我們不能明確地表示無限的對象. 但是關(guān)鍵的觀點是, 對于有限數(shù)據(jù)集, 我們?nèi)匀豢梢栽谀P椭袌?zhí)行后驗推斷, 而僅僅明確地表示它們的有限部分.
下面給出一些重要的組成貝葉斯非參數(shù)模型的構(gòu)建模塊:
高斯過程(Gaussian processes)
高斯過程是函數(shù)上的先驗, 使得在任何有限集合點處采樣的值是服從聯(lián)合高斯的. 在許多情況下, 為在函數(shù)上賦予先驗, 您需要假設(shè)后驗推理是易于處理的.Chinese restaurant process(CRP)
CRP是無限對象集合的劃分的先驗
這常被用于聚類模型, 使得簇的數(shù)目無需事先指定. 推理算法相當(dāng)簡單且易于理解, 所以沒有理由不使用CRP模型代替有限聚類模型.
這個過程可以等價于Dirichlet process.
Hierarchical Dirichlet process
包含一組共享相同base measure的Dirichlet process, baase measure本身也是從Dirichlet process中選取的.Indian buffet process(IBP)
IBP無限二進(jìn)制矩陣的先驗, 使得矩陣的每一行僅具有有限個1. 這是在每個對象可以擁有多個不同屬性時最常用的模型. 其中, 矩陣的行對應(yīng)于對象, 列對應(yīng)于屬性, 如果對象具有某屬性, 對應(yīng)列的元素為1.
最簡單的例子可能是IBP linear-Gaussian model. 其中, 觀察到的數(shù)據(jù)是屬性的線性函數(shù).
還可以根據(jù)beta process來看IBP過程. 本質(zhì)上, beta process之于IBP正如Dirichlet process之于CRP.
Dirichlet diffusion trees
一個分層聚類模型. 其中, 數(shù)據(jù)點以不同的粒度級別聚類. 即可能存在一些粗粒度的簇, 但是這些簇又可以分解成更細(xì)粒度的簇.Pitman-Yor process
類似于CRP, 但是在聚類大小上有更重尾的分布(比如冪律分布). 這說明您希望找到一些非常龐大的簇, 以及大量的小簇. 比起CRP選擇0的指數(shù)分布, 冪律分布對于許多真實數(shù)據(jù)有更好的擬合效果.
采樣算法
從"核心主題"章節(jié), 您已經(jīng)學(xué)習(xí)了兩個采樣算法:Gibbs采樣和Metropolis-Hastings(M-H)算法. Gibbs采樣涵蓋了很多簡單的情況, 但在很多模型中, 您甚至不能計算更新. 即使對于適用的模型, 如果不同的變量緊密耦合(tightly coupled), 采樣過程也會mix得非常緩慢. M-H算法是更一般的, 但是M-H算法的一般公式中沒有提供關(guān)于如何選擇提議分布(proposals)的指導(dǎo), 并且為實現(xiàn)良好的mix, 通常需要非常仔細(xì)地選擇提議分布.
下面是一些更先進(jìn)的MCMC算法, 這些算法在特定情形中表現(xiàn)更為良好:
collapsed Gibbs sampling
變量的一部分在理論上被邊緣化(marginalized)或折疊(collapsed)掉, 并在剩下的變量上進(jìn)行Gibbs采樣. 例如, 當(dāng)擬合CRP聚類模型時, 我們通常將聚類參數(shù)邊緣化掉, 并對聚類分配執(zhí)行Gibbs采樣. 這可以顯著地改善mix, 因為聚類分配和簇參數(shù)是緊密耦合的.Hamiltonian Monte Carlo?(HMC)
連續(xù)空間中M-H算法的實例, 其使用對數(shù)概率的梯度來選擇更好的探索方向. 這是驅(qū)動?Stan的算法.slice sampling
一種從一維分布中采樣的輔助變量方法. 其關(guān)鍵賣點是算法不需要指定任何參數(shù). 因此, 它經(jīng)常與其他算法(例如HMC)結(jié)合, 否則將需要指定步長參數(shù).reversible jump MCMC
在不同維度的空間之間構(gòu)造M-H提議分布的方式. 最常見的用例是貝葉斯模型平均
雖然在實踐中使用的大多數(shù)采樣算法是MCMC算法, 但Sequential Monte Carlo(SMC)算法值得一提. 這是從一系列相關(guān)分布中近似采樣的另一類技術(shù).
最常見的例子可能是粒子濾波器(particle filter), 通常應(yīng)用于時間序列模型的推理算法. 它每次一步地考慮觀察數(shù)據(jù), 并且在每個步驟中, 用一組粒子表示潛在狀態(tài)的后驗
退火重要性采樣(Annealed importance sampling)?(AIS)是另一種SMC方法, 其通過一系列中間分布從簡單的初始分布(比如先驗)到難處理的目標(biāo)分布(例如后驗)逐漸"退火" 針對每個中間分布執(zhí)行MCMC轉(zhuǎn)換. 由于在初始分布附近mixing通常更快, 這應(yīng)該有助于采樣器避免困在局部模式中.
算法計算一組權(quán)重, 這些權(quán)重亦可被用于?估計邊際似然(estimate the marginal likelihood). 當(dāng)使用了足夠多的中間分布時, 權(quán)重的方差會很小, 因此產(chǎn)生了一個精確的邊際似然估計.
變分推斷(Variational inference)
變分推斷是基于優(yōu)化而不是采樣的另一類近似推斷方法. 其基本想法是用一個易處理的近似分布來逼近難處理的后驗分布. 選擇近似分布的參數(shù)以使近似分布和后驗分布之間的距離的某些度量(通常使用KL散度)最小化.
我們很難對變分推斷和采樣方法之間的折中作出任何一般性的陳述, 因為這些都是一個廣泛的類別, 其中包括了許多特殊的算法, 既有簡單的又有復(fù)雜的. 然而, 有一些一般的經(jīng)驗規(guī)則:
變分推斷算法具有與采樣方法不同的實現(xiàn)困難
變分推斷算法更難, 因為它們需要冗長的數(shù)學(xué)推導(dǎo)來確定更新規(guī)則.
然而, 一旦實現(xiàn), 變分貝葉斯方法可以更容易地被檢驗, 因為可以對優(yōu)化代碼采用標(biāo)準(zhǔn)檢查(梯度檢查, 局部最優(yōu)測試等).
此外, 大多數(shù)變分推斷算法收斂到(局部)最優(yōu)解, 這消除了檢查收斂診斷的需要.
大多數(shù)變分推理分布的輸出是一個分布, 而不是樣本.
為了回答許多問題, 例如模型參數(shù)的期望或者方差, 可以簡單地檢查變分分布. 相比之下, 采樣方法通常需要收集大量采樣樣本, 這可能需要很大的開銷.
然而, 使用變分法, 近似的精度受到近似分布族的表達(dá)能力的限制, 并且近似分布與后驗分布有多大不同并不總是那么明顯. 相反, 如果您運(yùn)行一個采樣算法足夠長時間, 最終您會得到較為準(zhǔn)確的結(jié)果.
這里給出一些變分推斷算法的重要例子:
變分貝葉斯(variational Bayes)
貝葉斯模型的變分推斷應(yīng)用, 其中參數(shù)的后驗分布不能精確地表示, 如果模型還包括潛在變量, 則可以使用變分貝葉斯EM算法(variational Bayes EM)平均場近似(mean field approximation)
近似分布具有特別簡單的形式:假定所有變量是獨立的.
平均場也可以根據(jù)?凸對偶性(convex duality)來觀察, 這將導(dǎo)出與普通解釋不同的拓展
期望傳播(expectation propagation)
對循環(huán)置信傳播(loopy belief propagation)的一種近似. 它發(fā)送近似消息, 這些消息僅代表相關(guān)變量的充分統(tǒng)計量的期望.
下面給出一些使用變分推斷方法的經(jīng)典例子. 盡管你可能不會直接使用這些模型, 但是它們給出了變分技巧如何更一般地用于貝葉斯模型的指引:
線性回歸(linear regression)
邏輯回歸(logistic regression)
混合高斯(mixture of Gaussians)
指數(shù)族模型(exponential family models)
信念傳播(Belief propagation)
信念傳播是用于如貝葉斯網(wǎng)絡(luò)(Bayes nets)?和馬爾科夫場(Markov random fields)?(MRFs)等圖模型的另一類推斷算法. 模型中的變量相互"傳遞消息", 它們總結(jié)了關(guān)于其他變量的聯(lián)合分布的信息. 信念傳播有兩種一般形式:
當(dāng)應(yīng)用于樹結(jié)構(gòu)圖模型時, BP執(zhí)行精確的后驗推斷. 有兩種特殊的形式:
the?sum-product algorithm
計算每個單獨變量(以及每一對相鄰變量)的邊際分布.the?max-product algorithm
計算所有變量的最可能的聯(lián)合分配
還可以在不是樹結(jié)構(gòu)的圖中應(yīng)用相同的消息傳遞規(guī)則. 這沒有給出確切的結(jié)果, 事實上甚至缺少基本的保證, 例如收斂到固定點, 但通常它在實踐中能很有效. 這通常被稱為循環(huán)信念傳播(loopy belief propagation), 以區(qū)別于樹結(jié)構(gòu)的版本, 但令人困惑的是, 一些研究人員簡單地將其稱為"信念傳播"。
連接樹算法(junction tree algorithm)給出了通過定義粗糙的"超變量(super-variables)"來對非樹結(jié)構(gòu)圖應(yīng)用精確的BP的方法. 定義"超變量"后的圖是樹結(jié)構(gòu)的.
樹上的BP最常見的特殊情況是HMMs的前向-后向算法(forward-backward algorithm)?.卡爾曼平滑(Kalman smoothing)也是前向-后向算法的一種特例, 因此也是一種BP.
BP在計算機(jī)視覺和信息論中被廣泛使用, 在這兩個領(lǐng)域中, 推斷問題往往具有規(guī)則的結(jié)構(gòu). 在貝葉斯機(jī)器學(xué)習(xí)中, BP不常被單獨使用, 但是它可以是基于變分或采樣的算法中的強(qiáng)大組成部分.
理論
最后, 給出貝葉斯方法中的一些理論問題.定義貝葉斯模型需要指定先驗. 如果對于參數(shù)沒有較大的先驗信念, 我們可能希望選擇?無信息先驗(uninformative priors). 一個常見的選擇是Jeffreys prior.準(zhǔn)確地估計模型中的參數(shù)需要多少數(shù)據(jù)?最大似然的漸進(jìn)(asymptotics of maximum likelihood)?提供了對于這個問題的許多洞見, 因為對于有限模型, 后驗分布具有與最大似然估計的分布相似的漸進(jìn)行為。
往期精彩:
【原創(chuàng)首發(fā)】機(jī)器學(xué)習(xí)公式推導(dǎo)與代碼實現(xiàn)30講.pdf
【原創(chuàng)首發(fā)】深度學(xué)習(xí)語義分割理論與實戰(zhàn)指南.pdf
