浮點數(shù)精度丟失問題詳解
請看以下Go代碼，會返回 0.7 嗎？
var num float32
for i := 0; i < 7; i++{
num = num + 0.1
}
fmt.Println(num)
答案可能出人意料，是：0.70000005
0.70000005
也許有人會問，是不是Go語言的問題？換其他語言試試？OK，我們換JS試試。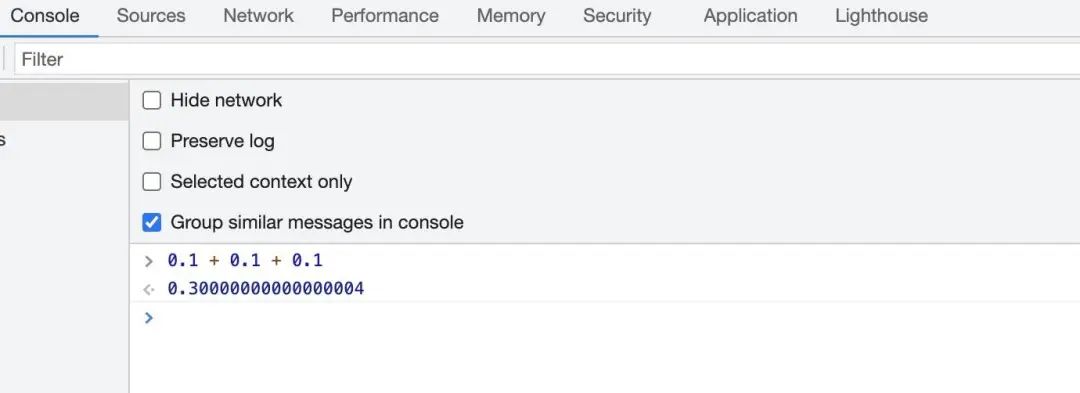
答案依然令人意外。除此之外，你還可以試試C、C++、Java、PHP等其他語言的float類型相加，看得到的數(shù)據(jù)是否精確；
還有，除了語言之外，你還可以在MySQL等數(shù)據(jù)庫中試試float類型數(shù)據(jù)的字段疊加，得到的數(shù)據(jù)是否精確。
我可以先告訴你答案：只要是float類型的數(shù)據(jù)相加，無論在任何語言、任何數(shù)據(jù)庫、任何中間件中進(jìn)行加法(減法乘除法)運算，得到的數(shù)據(jù)，都不會精確。
這是浮點類型的精度丟失現(xiàn)象。(Loss of significance)
要了解產(chǎn)生這個現(xiàn)象的原因，就要先了解計算機(jī)是如何定義和表示float類型的。不同于正整數(shù)類型的表示方法，float類型在計算機(jī)中的表示略顯復(fù)雜，遵循的是 IEEE754標(biāo)準(zhǔn)。
下面，我們就講一下 IEEE754標(biāo)準(zhǔn)。
我們首先回顧一下整數(shù)類型在計算機(jī)中的表示。我們知道:計算機(jī)只認(rèn)識0和1；那么，對于像6一樣的這種正整數(shù)，我們要做十進(jìn)制到二進(jìn)制的轉(zhuǎn)換。即：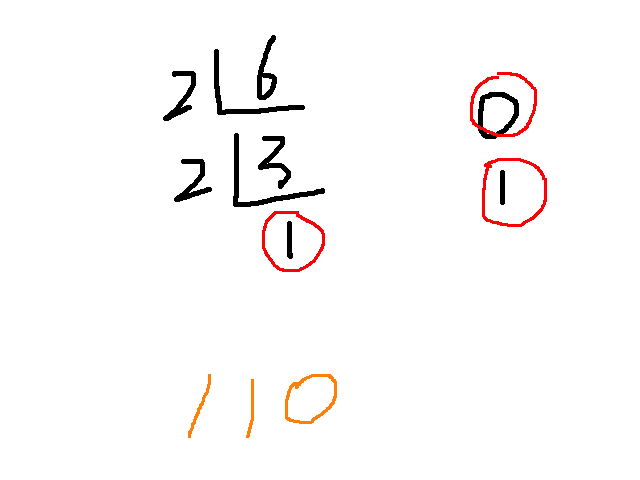
所以，十進(jìn)制 6最終轉(zhuǎn)化為二進(jìn)制為 110。
這很好理解，但是，如何表示 6.1等這類小數(shù)呢？有人說了，可以找個特殊的符號，用來表示小數(shù)點 .，把 6.1中 6和 1隔開；聽起來是個不錯的辦法。其實 IEEE754還真就是這么做的，只不過思路略有些復(fù)雜，總體思路就是：仿照用"科學(xué)計數(shù)法"！
我們再回顧一下什么是 科學(xué)計數(shù)法。把一個數(shù)表示成a與10的n次冪相乘的形式（1≤|a|<10，a不為分?jǐn)?shù)形式，n為整數(shù)），這種記數(shù)法叫做科學(xué)記數(shù)法。也就是：1.360X10^4 這種計數(shù)方式。
我們可以仿照科學(xué)計數(shù)法，來表示浮點數(shù)，把二進(jìn)制數(shù)統(tǒng)一表示成 1.0110101X2^n這種形式。數(shù)據(jù)層面怎么表示出這種形式呢？根據(jù) IEEE754的標(biāo)準(zhǔn)，將數(shù)據(jù)分為三部分：
從左到右分別表示：符號位(正負(fù)數(shù))、指數(shù)位和小數(shù)位
以單精度浮點數(shù)為例，單精度浮點數(shù)一共32位(雙精度64位，即平時所說的 double類型)，具體內(nèi)部表示為：
1個bit表示符號位
8個bit表示指數(shù)位
23個bit表示小數(shù)位
這里有個地方要特別注意：因為數(shù)據(jù)最終要表示成 1.0110101X2^n這種形式，整數(shù)位在二進(jìn)制下，永遠(yuǎn)都是 1，所以在表示float類型的時候，直接把 1給去掉了，假如有就占據(jù)一個bit的空間，既然那個bit位上永遠(yuǎn)都是1，所以干脆去掉了。
那么，具體該如何展示呢？例如小數(shù)點后的數(shù)字怎么表示？6.1能否寫成 110.1呢？如果能的話小數(shù)點后這個1代表什么呢？個數(shù)一？那添加幾個零的話，能否認(rèn)為是十、一百、一千？似乎是不可以，因為這樣只能滿足"視覺效果",邏輯層面直接說不通。
要明白在小數(shù)點后的數(shù)字代表除以2后的數(shù)字，例如二進(jìn)制下小數(shù)點后的第一位1代表 1 / 2等于 0.5，第二位1代表 1/2/2等于 0.25，依次類推第三位1則代表 0.125...具體請看下圖：
所以，給定一個小數(shù)，譬如 0.1，要想得到對應(yīng)的二進(jìn)制數(shù)，應(yīng)該是和小數(shù)點左邊的計算方式相反：乘以2，記錄整數(shù)位
0.1 X 2 = 0.2 0
0.2 X 2 = 0.4 0
0.4 X 2 = 0.8 0
0.8 X 2 = 1.6 1
(1.6 - 1 = 0.6)
0.6 X 2 = 1.2 1
(1.2 - 1 = 0.2)
0.2 X 2 = 0.4 0
0.4 X 2 = 0.8 0
0.8 X 2 = 1.6 1
(1.6 - 1 = 0.6)
0.6 X 2 = 1.2 1
(1.2 - 1 = 0.2)
0.2 X 2 = 0.4 0
0.4 X 2 = 0.8 0
0.8 X 2 = 1.6 1
...
// 無限循環(huán)下去
所以， 0.1 用二進(jìn)制表示為：0.000110011001100110011...因此 6.1 用二進(jìn)制應(yīng)該表示為：110.000110011001100110011...用”科學(xué)計數(shù)法“表示為：1.10000110011001100110011...X2^2OK，看來小數(shù)位的數(shù)可以確定了是 10000110011001100110011，即去掉整數(shù)位1后，向后截取的23位數(shù)(浮點數(shù)不精確的本質(zhì)原因)。
符號位0表示正數(shù)，1表示負(fù)數(shù)，所以可以確定是 6.1的符號位是0；現(xiàn)在符號位有了，小數(shù)位有了，只剩下指數(shù)2如的表示了，該如何表示呢？直接在8位的空間內(nèi)轉(zhuǎn)化為 000000010？
顯然不可以，首先，如果指數(shù)位用 原碼表示，那么，針對指數(shù)位為負(fù)的情況，就得加一個符號位去表示，而且還會出現(xiàn)兩個零的情況：00000000和 1000000，操作起來過程復(fù)雜~
有人要問那如果使用補(bǔ)碼呢？如果使用補(bǔ)碼，會出現(xiàn)以下情況，請看例子：
1.01 X 2^-1 和 1.11 X 2^3比較大小？
指數(shù)：
-1 和 3，分別轉(zhuǎn)化為二進(jìn)制數(shù) “111”和“011”；
"111"是"7"，"011"是"3"， 7會小于3嗎？
可見使用補(bǔ)碼，也不是很方便，于是，引用了另外一種編碼方式——-移碼。先說說移碼的定義：將每一個數(shù)值加上一個偏置常數(shù)(Excess/bias)，通常，當(dāng)編碼位數(shù)為n的時候，bias取"2^n-1"或者"2^n-1 - 1"
承接以上1.01 X 2^-1 和 1.11 X 2^3比較大小的例子：
1.01 X 2^-1 和 1.11 X 2^3大小？
指數(shù)：
-1 + 4 = 3，二進(jìn)制表示為:"011"
3 + 4 = 7 二進(jìn)制表示為："111"
7 > 3，即 "111" > "011" 比較完畢
就這樣，浮點數(shù)”科學(xué)計數(shù)法“的指數(shù)位比較變得簡單了，而且，消除了”正零“ 和 ”負(fù)零“ 不相同的問題。
因為 ：
假設(shè)偏移量是：4
則移碼表示的0只有：0 + 4 = 4，即“100”
在 IEEE754中，指數(shù)位移碼的偏移量為指數(shù)位數(shù)的 2^n-1-1，為127。
所以，回到 6.1表示的問題上，指數(shù)位為：2+127=129，二進(jìn)制表示為：10000001
因此， 6.1在 IEEE754單精度浮點數(shù)標(biāo)準(zhǔn)的下，表示為：
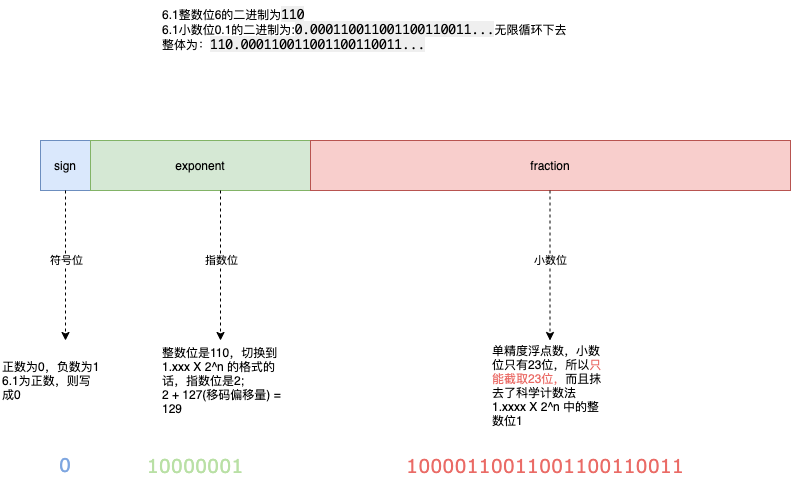
好了，現(xiàn)在了解了浮點數(shù) IEEE754標(biāo)準(zhǔn)的表示方法，知道為何浮點數(shù)相加總是不精確了吧？
因為浮點數(shù)很多小數(shù)在二進(jìn)制環(huán)境下很多都無法完整的表示，只能截取部分?jǐn)?shù)據(jù)來近似的表示，兩個數(shù)相加的話，就是兩個近似的數(shù)相加的和，如果相加次數(shù)足夠多，精確度自然也就會越來越低
推薦閱讀