深入理解GBDT回歸算法
點擊上方“小白學(xué)視覺”,選擇加"星標"或“置頂”
重磅干貨,第一時間送達
來源:公眾號?Microstrong?授權(quán)轉(zhuǎn)載
目錄:
1. GBDT簡介
2. GBDT回歸算法
? ? 2.1 GBDT回歸算法推導(dǎo)
? ? 2.2 GBDT回歸算法實例?
3. 手撕GBDT回歸算法 ? ?
? ? 3.1 用Python3實現(xiàn)GBDT回歸算法 ??
? ? 3.2 用sklearn實現(xiàn)GBDT回歸算法?
4. GBDT回歸任務(wù)常見的損失函數(shù)?
5. GBDT的正則化?
6. 關(guān)于GBDT若干問題的思考
7. 總結(jié)?
8. Reference
本文的主要內(nèi)容概覽:
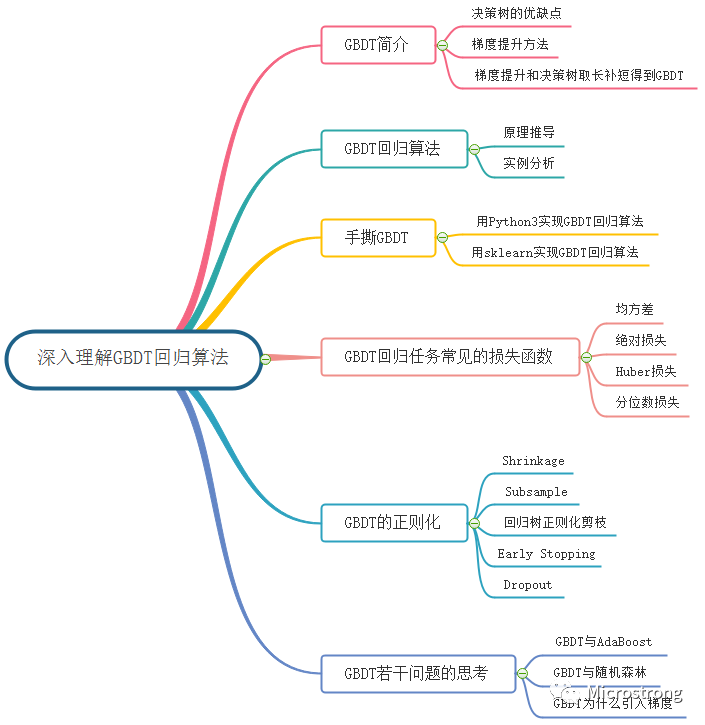
1. GBDT簡介
決策樹有以下優(yōu)點:
決策樹可以認為是if-then規(guī)則的集合,易于理解,可解釋性強,預(yù)測速度快。
決策樹算法相比于其他的算法需要更少的特征工程,比如可以不用做特征標準化。
決策樹可以很好的處理字段缺失的數(shù)據(jù)。
決策樹能夠自動組合多個特征,也有特征選擇的作用。
對異常點魯棒
可擴展性強,容易并行。
決策樹有以下缺點:
缺乏平滑性(回歸預(yù)測時輸出值只能輸出有限的若干種數(shù)值)。
不適合處理高維稀疏數(shù)據(jù)。
單獨使用決策樹算法時容易過擬合。
2. GBDT回歸算法
2.1 GBDT回歸算法推導(dǎo)
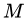 棵樹組成的加法模型,其對應(yīng)的公式如下:
棵樹組成的加法模型,其對應(yīng)的公式如下: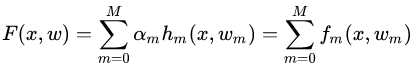
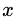 為輸入樣本;
為輸入樣本;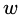 為模型參數(shù);
為模型參數(shù);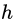 為分類回歸樹;
為分類回歸樹;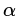 為每棵樹的權(quán)重。GBDT算法的實現(xiàn)過程如下:
為每棵樹的權(quán)重。GBDT算法的實現(xiàn)過程如下:給定訓(xùn)練數(shù)據(jù)集: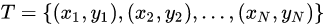 ?其中,?
?其中,?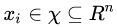 ,
,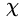 為輸入空間,
為輸入空間,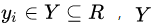 為輸出空間,損失函數(shù)為
為輸出空間,損失函數(shù)為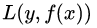 ,我們的目標是得到最終的回歸樹
,我們的目標是得到最終的回歸樹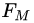 。
。
(1)初始化第一個弱學(xué)習(xí)器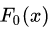 :
:
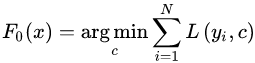
(2)對于建立M棵分類回歸樹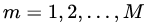 :
:
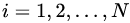 ,計算第
,計算第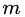 棵樹對應(yīng)的響應(yīng)值(損失函數(shù)的負梯度,即偽殘差):
棵樹對應(yīng)的響應(yīng)值(損失函數(shù)的負梯度,即偽殘差):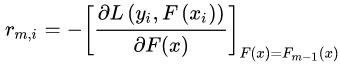
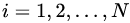 ,利用CART回歸樹擬合數(shù)據(jù)
,利用CART回歸樹擬合數(shù)據(jù)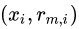 ,得到第
,得到第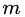 棵回歸樹,其對應(yīng)的葉子節(jié)點區(qū)域為
棵回歸樹,其對應(yīng)的葉子節(jié)點區(qū)域為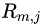 ,其中
,其中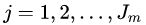 ,且
,且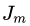 ?為第
?為第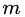 棵回歸樹葉子節(jié)點的個數(shù)。
棵回歸樹葉子節(jié)點的個數(shù)。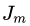 個葉子節(jié)點區(qū)域?
個葉子節(jié)點區(qū)域?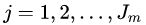 ,計算出最佳擬合值:
,計算出最佳擬合值: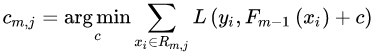
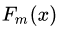 :
: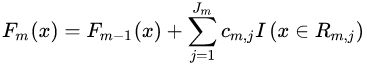
(3)得到強學(xué)習(xí)器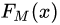 的表達式:
的表達式:
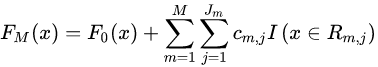
2.2 GBDT回歸算法實例
(1)數(shù)據(jù)集介紹
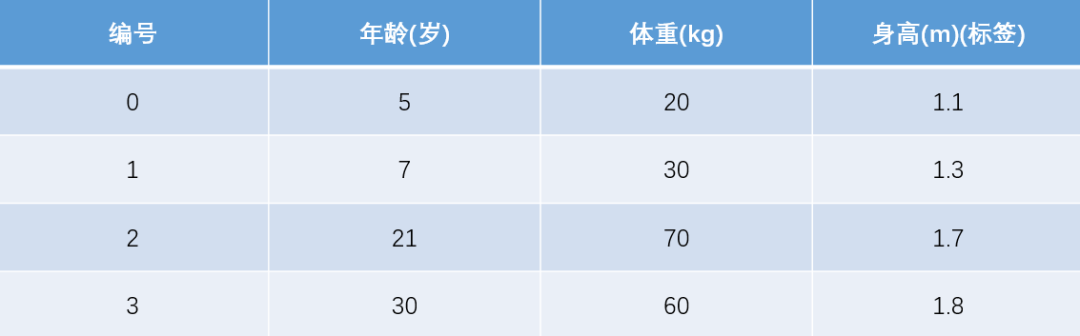

(2)模型訓(xùn)練階段
參數(shù)設(shè)置:
學(xué)習(xí)率:learning_rate = 0.1
迭代次數(shù):n_trees = 5
樹的深度:max_depth = 3
1)初始化弱學(xué)習(xí)器:
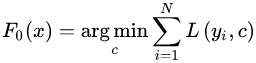
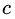 。
。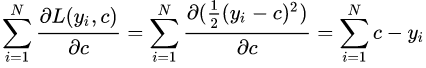
令導(dǎo)數(shù)等于0:
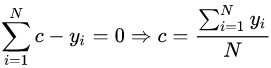
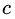 取值為所有訓(xùn)練樣本標簽值的均值。
取值為所有訓(xùn)練樣本標簽值的均值。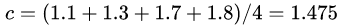 ,此時得到的初始化學(xué)習(xí)器為
,此時得到的初始化學(xué)習(xí)器為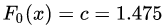 。
。2)對于建立M棵分類回歸樹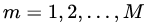 :
:
首先計算負梯度,根據(jù)上文損失函數(shù)為平方損失時,負梯度就是殘差,也就是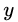 與上一輪得到的學(xué)習(xí)器
與上一輪得到的學(xué)習(xí)器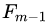 的差值:
的差值:
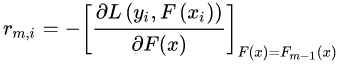
現(xiàn)將殘差的計算結(jié)果列表如下:
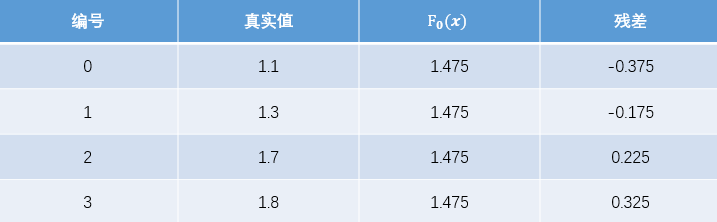
此時將殘差作為樣本的真實值來訓(xùn)練弱學(xué)習(xí)器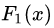 ,即下表數(shù)據(jù):
,即下表數(shù)據(jù):
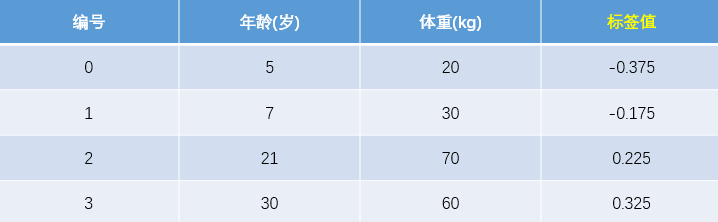
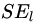 為左節(jié)點的平方損失,
為左節(jié)點的平方損失,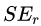 ?為右節(jié)點的平方損失,找到使平方損失和?
?為右節(jié)點的平方損失,找到使平方損失和?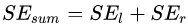 最小的那個劃分節(jié)點,即為最佳劃分節(jié)點。
最小的那個劃分節(jié)點,即為最佳劃分節(jié)點。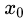 ,右節(jié)點包括樣本
,右節(jié)點包括樣本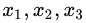 ,則
,則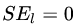 、
、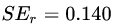 、
、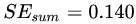 ,所有可能的劃分情況如下表所示:
,所有可能的劃分情況如下表所示: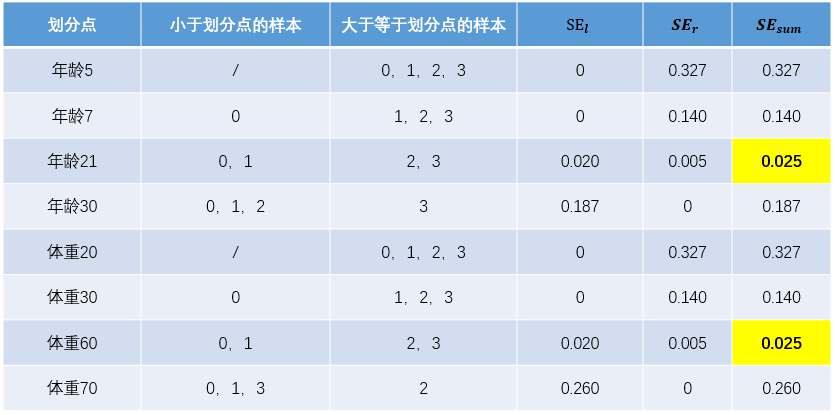
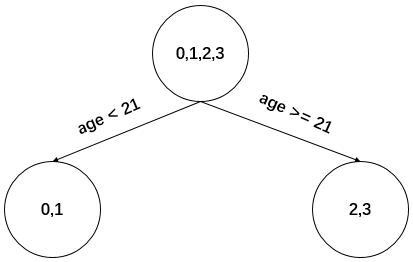
對于左節(jié)點,只含有0,1兩個樣本,根據(jù)下表結(jié)果我們選擇年齡7為劃分點(也可以選體重30)。
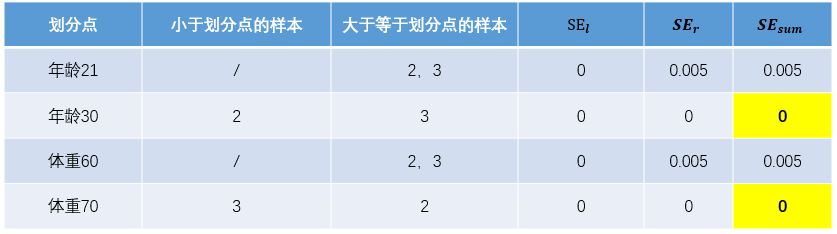
對于右節(jié)點,只含有2,3兩個樣本,根據(jù)下表結(jié)果我們選擇年齡30為劃分點(也可以選體重70)。
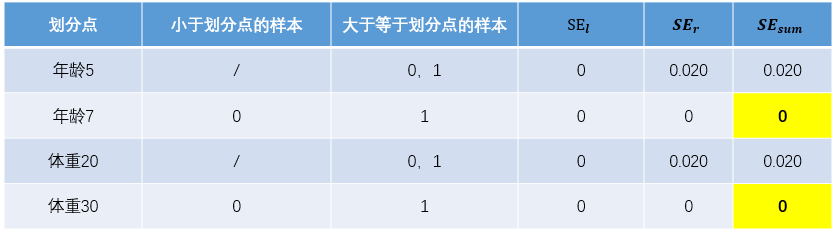
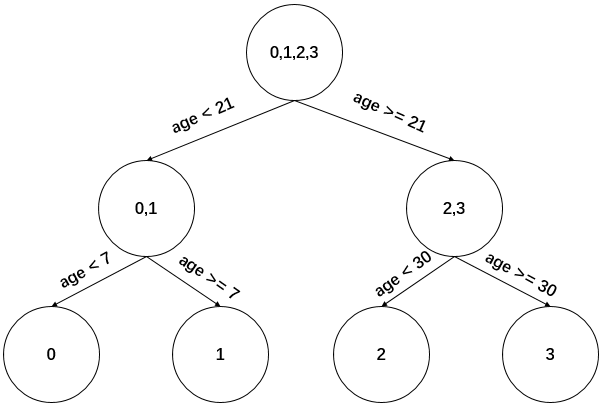
現(xiàn)在我們的第一棵回歸樹長下面這個樣子:
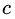 ,來擬合殘差。
,來擬合殘差。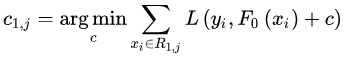
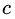 ,其實就是標簽值的均值。這個地方的標簽值不是原始的
,其實就是標簽值的均值。這個地方的標簽值不是原始的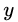 ,而是本輪要擬合的標殘差
,而是本輪要擬合的標殘差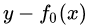 。
。
此時的樹長這下面這個樣子:
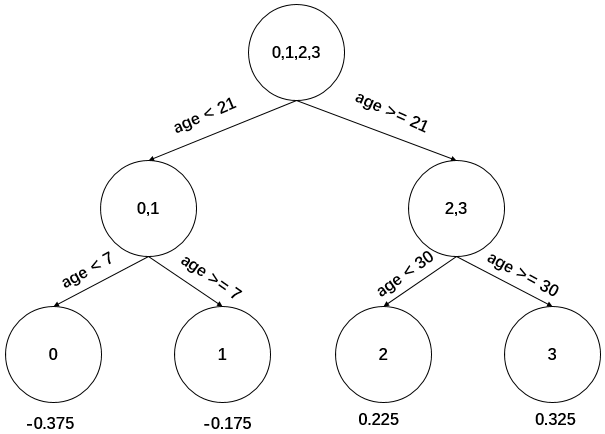
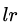 表示。更新公式為:
表示。更新公式為: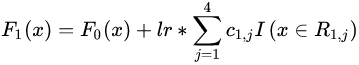
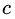 ,即學(xué)習(xí)率為1,很容易一步學(xué)到位導(dǎo)致GBDT過擬合。
,即學(xué)習(xí)率為1,很容易一步學(xué)到位導(dǎo)致GBDT過擬合。重復(fù)此步驟,直到? ?結(jié)束,最后生成5棵樹。
?結(jié)束,最后生成5棵樹。
下面將展示每棵樹最終的結(jié)構(gòu),這些圖都是我GitHub上用Python3實現(xiàn)GBDT代碼生成的,感興趣的同學(xué)可以去運行一下代碼。地址:https://github.com/Microstrong0305/WeChat-zhihu-csdnblog-code/tree/master/Ensemble%20Learning/GBDT_Regression
第一棵樹:
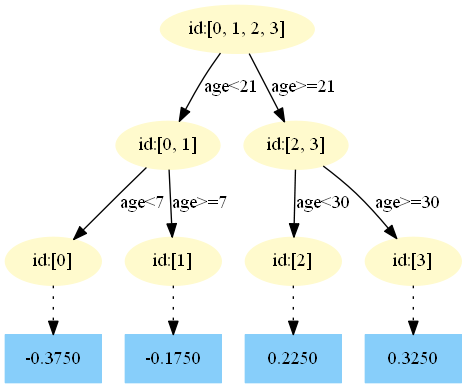
第二棵樹:
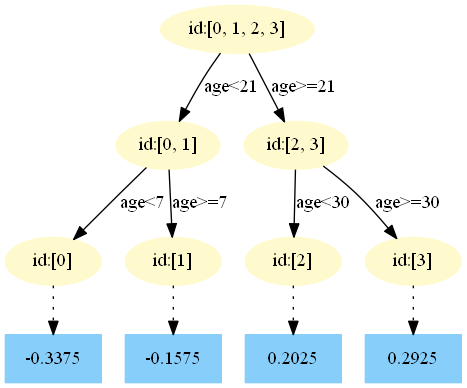
第三棵樹:
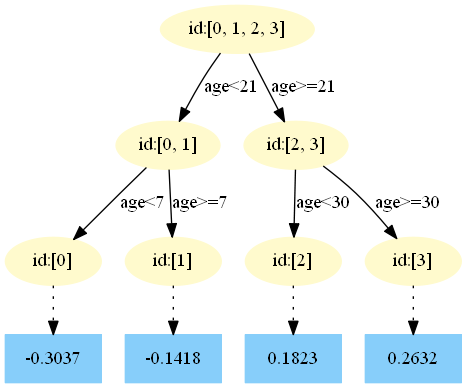
第四棵樹:
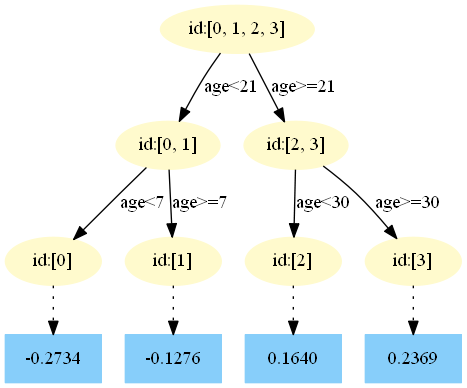
第五棵樹:
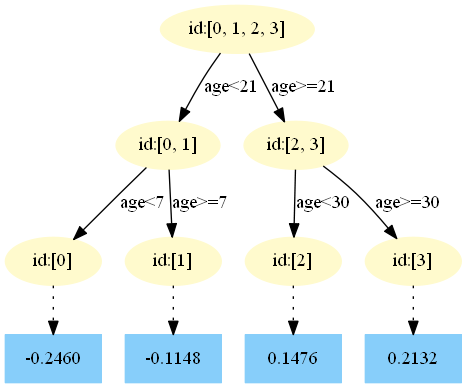
3)得到最后的強學(xué)習(xí)器:
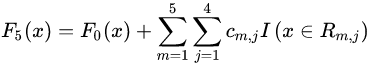
(3)模型預(yù)測階段
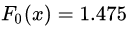
在
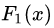 中,測試樣本的年齡為25,大于劃分節(jié)點21歲,又小于30歲,所以被預(yù)測為0.2250。
中,測試樣本的年齡為25,大于劃分節(jié)點21歲,又小于30歲,所以被預(yù)測為0.2250。在
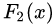 ?中,測試樣本的年齡為25,大于劃分節(jié)點21歲,又小于30歲,所以被預(yù)測為0.2025。
?中,測試樣本的年齡為25,大于劃分節(jié)點21歲,又小于30歲,所以被預(yù)測為0.2025。在?
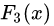 中,測試樣本的年齡為25,大于劃分節(jié)點21歲,又小于30歲,所以被預(yù)測為0.1823。
中,測試樣本的年齡為25,大于劃分節(jié)點21歲,又小于30歲,所以被預(yù)測為0.1823。在
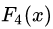 中,測試樣本的年齡為25,大于劃分節(jié)點21歲,又小于30歲,所以被預(yù)測為0.1640。
中,測試樣本的年齡為25,大于劃分節(jié)點21歲,又小于30歲,所以被預(yù)測為0.1640。在
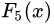 中,測試樣本的年齡為25,大于劃分節(jié)點21歲,又小于30歲,所以被預(yù)測為0.1476。
中,測試樣本的年齡為25,大于劃分節(jié)點21歲,又小于30歲,所以被預(yù)測為0.1476。
最終預(yù)測結(jié)果為:
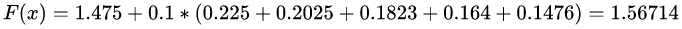
3. 手撕GBDT回歸算法
本篇文章所有數(shù)據(jù)集和代碼均在我的GitHub中,地址:https://github.com/Microstrong0305/WeChat-zhihu-csdnblog-code/tree/master/Ensemble%20Learning
3.1 用Python3實現(xiàn)GBDT回歸算法
需要的Python庫:
pandas、PIL、pydotplus、matplotlib3.2 用sklearn實現(xiàn)GBDT回歸算法
?
import numpy as npfrom sklearn.ensemble import GradientBoostingRegressorgbdt = GradientBoostingRegressor(loss='ls', learning_rate=0.1, n_estimators=5, subsample=1, min_samples_split=2, min_samples_leaf=1, max_depth=3, init=None, random_state=None, max_features=None, alpha=0.9, verbose=0, max_leaf_nodes=None, warm_start=False)train_feat = np.array([[1, 5, 20],[2, 7, 30],[3, 21, 70],[4, 30, 60],])train_id = np.array([[1.1], [1.3], [1.7], [1.8]]).ravel()test_feat = np.array([[5, 25, 65]])test_id = np.array([[1.6]])print(train_feat.shape, train_id.shape, test_feat.shape, test_id.shape)gbdt.fit(train_feat, train_id)pred = gbdt.predict(test_feat)total_err = 0for i in range(pred.shape[0]):print(pred[i], test_id[i])err = (pred[i] - test_id[i]) / test_id[i]total_err += err * errprint(total_err / pred.shape[0])

4. GBDT回歸任務(wù)常見的損失函數(shù)
(1)均方差,這個是最常見的回歸損失函數(shù)了,公式如下:
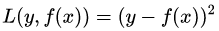
對應(yīng)的負梯度誤差為:
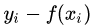
(2)絕對損失,這個損失函數(shù)也很常見,公式如下:
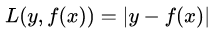
對應(yīng)的負梯度誤差為:
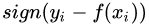
(3)Huber損失,它是均方差和絕對損失的折衷產(chǎn)物,對于遠離中心的異常點,采用絕對損失,而中心附近的點采用均方差。這個界限一般用分位數(shù)點度量。損失函數(shù)如下:
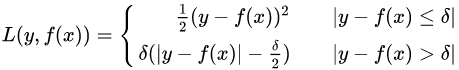
對應(yīng)的負梯度誤差為:
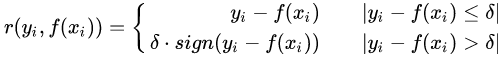
(4)分位數(shù)損失,它對應(yīng)的是分位數(shù)回歸的損失函數(shù),表達式為:
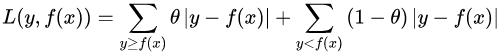
其中,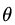 為分位數(shù),需要我們在回歸前指定。對應(yīng)的負梯度誤差為:
為分位數(shù),需要我們在回歸前指定。對應(yīng)的負梯度誤差為:
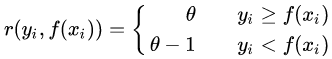
5. GBDT的正則化
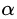 。系數(shù)
。系數(shù)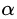 也被稱為學(xué)習(xí)率(learning rate),因為它可以對梯度提升的步長進行調(diào)整,也就是它可以影響我們設(shè)置的回歸樹個數(shù)。對于前面的弱學(xué)習(xí)器的迭代:
也被稱為學(xué)習(xí)率(learning rate),因為它可以對梯度提升的步長進行調(diào)整,也就是它可以影響我們設(shè)置的回歸樹個數(shù)。對于前面的弱學(xué)習(xí)器的迭代: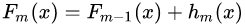
如果我們加上了正則化項,則有:
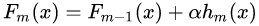
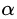 的取值范圍為?
的取值范圍為?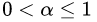 。對于同樣的訓(xùn)練集學(xué)習(xí)效果,較小的?
。對于同樣的訓(xùn)練集學(xué)習(xí)效果,較小的?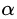 意味著我們需要更多的弱學(xué)習(xí)器的迭代次數(shù)。通常我們用學(xué)習(xí)率和迭代最大次數(shù)一起來決定算法的擬合效果。即參數(shù)learning_rate會強烈影響到參數(shù)n_estimators(即弱學(xué)習(xí)器個數(shù))。learning_rate的值越小,就需要越多的弱學(xué)習(xí)器數(shù)來維持一個恒定的訓(xùn)練誤差(training error)常量。經(jīng)驗上,推薦小一點的learning_rate會對測試誤差(test error)更好。在實際調(diào)參中推薦將learning_rate設(shè)置為一個小的常數(shù)(e.g. learning_rate <= 0.1),并通過early stopping機制來選n_estimators。
意味著我們需要更多的弱學(xué)習(xí)器的迭代次數(shù)。通常我們用學(xué)習(xí)率和迭代最大次數(shù)一起來決定算法的擬合效果。即參數(shù)learning_rate會強烈影響到參數(shù)n_estimators(即弱學(xué)習(xí)器個數(shù))。learning_rate的值越小,就需要越多的弱學(xué)習(xí)器數(shù)來維持一個恒定的訓(xùn)練誤差(training error)常量。經(jīng)驗上,推薦小一點的learning_rate會對測試誤差(test error)更好。在實際調(diào)參中推薦將learning_rate設(shè)置為一個小的常數(shù)(e.g. learning_rate <= 0.1),并通過early stopping機制來選n_estimators。6. 關(guān)于GBDT若干問題的思考
(1)GBDT與AdaBoost的區(qū)別與聯(lián)系?
(2)GBDT與隨機森林(Random Forest,RF)的區(qū)別與聯(lián)系?
(3)我們知道殘差=真實值-預(yù)測值,明明可以很方便的計算出來,為什么GBDT的殘差要用負梯度來代替?為什么要引入麻煩的梯度?有什么用呢?
7. 總結(jié)
8. Reference
由于參考的文獻較多,我把每一部分都重點參考了哪些文章詳細標注一下。
GBDT簡介與GBDT回歸算法:
【1】Friedman J H . Greedy Function Approximation: A Gradient Boosting Machine[J]. The Annals of Statistics, 2001, 29(5):1189-1232.
【2】Friedman, Jerome & Hastie, Trevor & Tibshirani, Robert. (2000). Additive Logistic Regression: A Statistical View of Boosting. The Annals of Statistics. 28. 337-407. 10.1214/aos/1016218223.
【3】機器學(xué)習(xí)-一文理解GBDT的原理-20171001 - 謀殺電視機的文章 - 知乎 https://zhuanlan.zhihu.com/p/29765582
【4】GBDT算法原理深入解析,地址:https://www.zybuluo.com/yxd/note/611571
【5】GBDT的原理和應(yīng)用 - 文西的文章 - 知乎 https://zhuanlan.zhihu.com/p/30339807
【6】ID3、C4.5、CART、隨機森林、bagging、boosting、Adaboost、GBDT、xgboost算法總結(jié) - yuyuqi的文章 - 知乎 https://zhuanlan.zhihu.com/p/34534004
【7】GBDT:梯度提升決策樹,地址:https://www.jianshu.com/p/005a4e6ac775
【8】機器學(xué)習(xí)算法中 GBDT 和 XGBOOST 的區(qū)別有哪些?- wepon的回答 - 知乎 https://www.zhihu.com/question/41354392/answer/98658997
【9】http://wepon.me/files/gbdt.pdf
【10】GBDT詳細講解&常考面試題要點,地址:https://mp.weixin.qq.com/s/M2PwsrAnI1S9SxSB1guHdg
【11】Gradient Boosting Decision Tree,地址:http://gitlinux.net/2019-06-11-gbdt-gradient-boosting-decision-tree/
【12】《推薦系統(tǒng)開發(fā)實戰(zhàn)》之基于點擊率預(yù)估的推薦算法介紹和案例開發(fā)實戰(zhàn),地址:https://mp.weixin.qq.com/s/2VATflDlelfxhOQkcXHSqw
【13】GBDT算法原理以及實例理解,地址:https://blog.csdn.net/zpalyq110/article/details/79527653
手撕GBDT回歸算法:
【14】GBDT_Simple_Tutorial(梯度提升樹簡易教程),GitHub地址:https://github.com/Freemanzxp/GBDT_Simple_Tutorial
【15】SCIKIT-LEARN與GBDT使用案例,地址:https://blog.csdn.net/superzrx/article/details/47073847
【16】手寫原始gbdt,地址:https://zhuanlan.zhihu.com/p/82406112?utm_source=wechat_session&utm_medium=social&utm_oi=743812915018104832
GBDT回歸任務(wù)常見的損失函數(shù)與正則化:
【17】Regularization on GBDT,地址:http://chuan92.com/2016/04/11/regularization-on-gbdt
【18】Early stopping of Gradient Boosting,地址:https://scikit-learn.org/stable/auto_examples/ensemble/plot_gradient_boosting_early_stopping.html
【19】Rashmi K V, Gilad-Bachrach R. DART: Dropouts meet Multiple Additive Regression Trees[C]//AISTATS. 2015: 489-497.?
關(guān)于GBDT若干問題的思考:
【20】關(guān)于adaboost、GBDT、xgboost之間的區(qū)別與聯(lián)系,地址:https://blog.csdn.net/HHTNAN/article/details/80894247
【21】[校招-基礎(chǔ)算法]GBDT/XGBoost常見問題 - Jack Stark的文章 - 知乎 https://zhuanlan.zhihu.com/p/81368182
【22】gbdt的殘差為什么用負梯度代替?- 知乎 https://www.zhihu.com/question/63560633
【23】gbdt的殘差為什么用負梯度代替?- 奧奧奧奧噢利的回答 - 知乎 https://www.zhihu.com/question/63560633/answer/581670747
下載1:OpenCV-Contrib擴展模塊中文版教程 在「小白學(xué)視覺」公眾號后臺回復(fù):擴展模塊中文教程,即可下載全網(wǎng)第一份OpenCV擴展模塊教程中文版,涵蓋擴展模塊安裝、SFM算法、立體視覺、目標跟蹤、生物視覺、超分辨率處理等二十多章內(nèi)容。 下載2:Python視覺實戰(zhàn)項目52講 在「小白學(xué)視覺」公眾號后臺回復(fù):Python視覺實戰(zhàn)項目,即可下載包括圖像分割、口罩檢測、車道線檢測、車輛計數(shù)、添加眼線、車牌識別、字符識別、情緒檢測、文本內(nèi)容提取、面部識別等31個視覺實戰(zhàn)項目,助力快速學(xué)校計算機視覺。 下載3:OpenCV實戰(zhàn)項目20講 在「小白學(xué)視覺」公眾號后臺回復(fù):OpenCV實戰(zhàn)項目20講,即可下載含有20個基于OpenCV實現(xiàn)20個實戰(zhàn)項目,實現(xiàn)OpenCV學(xué)習(xí)進階。 交流群
歡迎加入公眾號讀者群一起和同行交流,目前有SLAM、三維視覺、傳感器、自動駕駛、計算攝影、檢測、分割、識別、醫(yī)學(xué)影像、GAN、算法競賽等微信群(以后會逐漸細分),請掃描下面微信號加群,備注:”昵稱+學(xué)校/公司+研究方向“,例如:”張三?+?上海交大?+?視覺SLAM“。請按照格式備注,否則不予通過。添加成功后會根據(jù)研究方向邀請進入相關(guān)微信群。請勿在群內(nèi)發(fā)送廣告,否則會請出群,謝謝理解~

