深入理解邏輯回歸及公式推導(dǎo)
導(dǎo)讀
邏輯回歸是一種線性模型,更確切的說(shuō)是嵌套了一層sigmoid函數(shù)的線性模型。


寫在滕王閣下的一篇文章
分類和回歸是機(jī)器學(xué)習(xí)中兩類經(jīng)典的問(wèn)題,而邏輯回歸雖然叫回歸,卻是一個(gè)用于解決分類問(wèn)題的算法模型,但確實(shí)跟回歸有著密切關(guān)系——它的分類源于回歸擬合的思想。
解釋這個(gè)問(wèn)題,得首先從回歸和分類的特點(diǎn)說(shuō)起。
回歸,最簡(jiǎn)單的場(chǎng)景就是用身高擬合體重:給出一組身高數(shù)據(jù),通過(guò)訓(xùn)練可以擬合獲得期望下的體重與身高的線性關(guān)系。這里身高和體重都是連續(xù)數(shù)值,而且理論情況下這個(gè)擬合的算法模型并不限制輸入輸出范圍——回歸結(jié)果取值連續(xù)且無(wú)明確范圍,這是一個(gè)明顯有別于分類模型的特點(diǎn)。而分類則剛好相反:以最基本的二分類問(wèn)題為例,其學(xué)習(xí)結(jié)果只有0和1兩種,取值離散且結(jié)果有限。
進(jìn)一步的,仍以身高擬合體重的回歸問(wèn)題為例,若此時(shí)想要得到一個(gè)關(guān)于體重是重或輕的結(jié)論,也就是給出一個(gè)二值判斷,那么此時(shí)就變?yōu)橐粋€(gè)二分類問(wèn)題。最直接的思路是設(shè)定一個(gè)體重輕重的閾值:大于該值則判斷為重,否則判斷為輕——這也就是一個(gè)階躍函數(shù)即可解決的問(wèn)題。然而理想很美好,現(xiàn)實(shí)卻并不合適:因?yàn)闊o(wú)法直接確定這個(gè)合理的閾值為多少,需要用算法訓(xùn)練得出;而在用算法模型計(jì)算和推導(dǎo)過(guò)程中又由于階躍函數(shù)的不可導(dǎo)而使得這一問(wèn)題變得困難。
既要求能盡可能實(shí)現(xiàn)階躍函數(shù)的特性,又要在臨界值附近可導(dǎo),sigmoid函數(shù)應(yīng)運(yùn)而生,其幾乎可以完美擬合階躍函數(shù)的性質(zhì)。記擬合結(jié)果為,則在階躍函數(shù)中為,而在sigmoid函數(shù)中,。二者函數(shù)曲線對(duì)比如下圖所示。
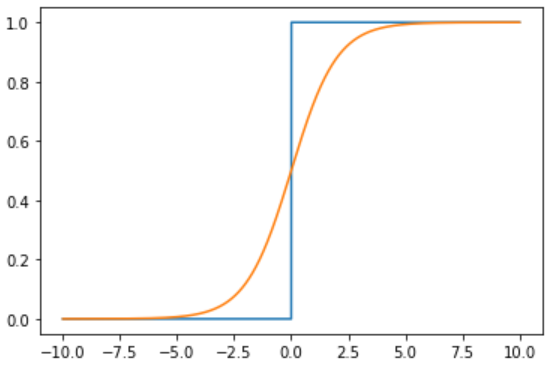
在前述體重輕重的判斷問(wèn)題中,由于橫軸可理解成由身高數(shù)據(jù)擬合出的體重結(jié)果,縱軸則是關(guān)于該體重是重或輕的二值判斷依據(jù),顯然隨著體重的增加判斷為重的概率越大。相較于用一個(gè)固定的閾值來(lái)硬區(qū)分輕重的方式,用這種概率的形式則有很多好處。
實(shí)際上,邏輯回歸相當(dāng)于首先執(zhí)行一次線性擬合的回歸問(wèn)題,然后再通過(guò)sigmoid函數(shù)將擬合結(jié)果轉(zhuǎn)化為二分類的概率問(wèn)題:
稍微對(duì)二者變換一下形式,即可得到:
不同于線性回歸中明確區(qū)分權(quán)重系數(shù)w和偏置b,邏輯回歸中為書寫方便,一般將b包含在w內(nèi),而統(tǒng)一寫作f(x)=wx的形式。
這個(gè)形式就比較明朗了:通過(guò)f(x) = wx進(jìn)行線性擬合,結(jié)果可以作為二分類中兩類概率比的對(duì)數(shù),概率比叫做幾率,取對(duì)數(shù)就是對(duì)數(shù)幾率,所以邏輯回歸的本質(zhì)就是線性回歸對(duì)數(shù)幾率的過(guò)程——即對(duì)數(shù)幾率回歸。而之所以叫邏輯回歸,則是因?yàn)閷⒕€性擬合結(jié)果套一層sigmoid函數(shù),這個(gè)函數(shù)又叫l(wèi)ogistic函數(shù),音譯邏輯回歸。
再解決了為什么叫邏輯回歸的問(wèn)題之后,第二個(gè)問(wèn)題就是邏輯回歸的損失函數(shù)。需要進(jìn)行參數(shù)的優(yōu)化的機(jī)器學(xué)習(xí)模型中,都需要定義相應(yīng)的損失函數(shù),例如SVM、線性回歸等。那么邏輯回歸的損失函數(shù)是什么呢?
注:損失函數(shù)用于描述單樣本預(yù)測(cè)結(jié)果與真實(shí)結(jié)果的偏差程度,代價(jià)函數(shù)是所有樣本損失的統(tǒng)計(jì)值,而目標(biāo)函數(shù)則是代價(jià)函數(shù)和模型復(fù)雜度的加和。
這里首先給出邏輯回歸的損失函數(shù)形式:
一般存在以下兩種理解:
1)基于極大似然估計(jì)的理解:
前面得出,邏輯回歸實(shí)質(zhì)上是擬合對(duì)數(shù)幾率的回歸過(guò)程,而為了最大化這個(gè)概率,也就是相當(dāng)于y=1時(shí),最大化h1(x),y=0時(shí),最大化h0(x),將二者巧妙的合并一起可表達(dá)為:
考慮所有樣本的聯(lián)合概率最大化,那么等價(jià)于:
2)基于損失函數(shù)意義構(gòu)造:
其實(shí)這是一種先有目標(biāo)結(jié)果后有構(gòu)造過(guò)程。既然損失函數(shù)是描述預(yù)測(cè)結(jié)果與真實(shí)值的差距,當(dāng)y=1時(shí),預(yù)測(cè)結(jié)果為h1(x),該值越大意味著越與真實(shí)值1相近,損失越小;反之,當(dāng)y=0時(shí),預(yù)測(cè)結(jié)果為h0(x)=1-h1(x),該值越大意味著越與真實(shí)值0相近,損失越小,那么仍然沿用上面的技巧,即先分別構(gòu)造兩種分類下的損失函數(shù),而后再巧妙的結(jié)合在一起:
y=1時(shí),h1(x)越接近1,意味著最終判為1的概率越大,越接近真實(shí)標(biāo)簽,損失越接近于0
y=0時(shí),h1(x)越接近0,意味著最終判為0的概率越大,越接近真實(shí)標(biāo)簽,損失越接近于0
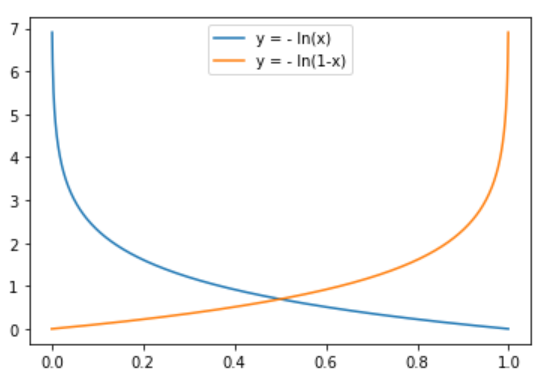
構(gòu)造兩種分類下的對(duì)數(shù)形式損失函數(shù)曲線
發(fā)現(xiàn),對(duì)數(shù)形式的函數(shù)曲線剛好滿足以上預(yù)期,所以就有了邏輯回歸的損失函數(shù),當(dāng)然這里也分別用了各自情況下的損失函數(shù)與相應(yīng)標(biāo)簽乘積的加和作為單樣本的損失。
實(shí)際上,雖然關(guān)于邏輯回歸的損失函數(shù)一直以來(lái)有這兩種解讀,但其實(shí)這是一個(gè)非常典型的分類損失函數(shù),即交叉熵?fù)p失函數(shù)。
在明確了邏輯回歸算法的損失函數(shù)后,那么剩下的就是如何迭代求解了。其實(shí)這個(gè)過(guò)程本身不難,重點(diǎn)是要搞清楚變量是如何傳遞求導(dǎo)的。當(dāng)然,首先要知道這里要優(yōu)化的參數(shù)實(shí)際上是系數(shù)向量W,更準(zhǔn)確的說(shuō)其中包含了偏置b的W。
這里首選給出一個(gè)輔助的求導(dǎo)中間過(guò)程,也是sigmoid函數(shù)的一個(gè)性質(zhì):
這個(gè)實(shí)際上就是權(quán)重系數(shù)w在更新過(guò)程中的梯度,進(jìn)一步應(yīng)用梯度下降法,可得到w的更新公式為:
此即為梯度下降法。其中,根據(jù)每次迭代更新過(guò)程中用到樣本的數(shù)量,又進(jìn)一步細(xì)分為批量梯度下降法(部分樣本參與訓(xùn)練)、隨機(jī)梯度下降法(隨機(jī)抽取一個(gè)樣本參與訓(xùn)練)。
邏輯回歸雖然涉及到公式較多,但其實(shí)完整理解下來(lái)還是比較順暢的,而且對(duì)于一些經(jīng)典的二分類問(wèn)題,也因其較強(qiáng)的可解釋性、計(jì)算簡(jiǎn)單和不錯(cuò)的模型效果,而廣為使用。進(jìn)一步深入思考發(fā)現(xiàn),邏輯回歸的流程如下圖所示:
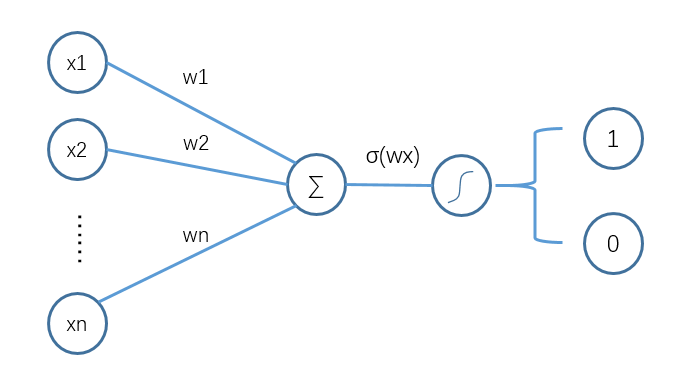
邏輯回歸執(zhí)行流程
巧了,這不剛好就是單層神經(jīng)網(wǎng)絡(luò)嘛!
相關(guān)閱讀:
