字符串硬核講解
作者丨sowhat1412
來(lái)源丨sowhat1412
1 暴力破解法
在主串A中查找模式串B的出現(xiàn)位置,其中如果A的長(zhǎng)度是n,B的長(zhǎng)度是m,則n > m。當(dāng)我們暴力匹配時(shí),在主串A中匹配起始位置分別是 0、1、2….n-m 且長(zhǎng)度為 m 的 n-m+1 個(gè)子串。
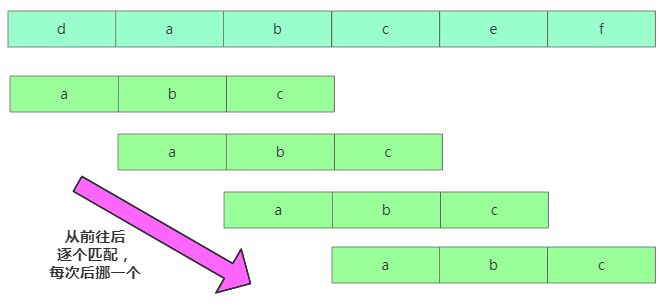
對(duì)應(yīng)代碼是:
#include<stdio.h>
#include<string.h>
int cnt=0;
int index(char s[], char sub[])
{
int i=0;
int j=0;
while(i<strlen(s))
{
if(s[i]==sub[j])
{ //單個(gè)字符相等的話 i和j都向后搜索
i++;
j++;
}
else
{ //有字符不匹配的話,i從上一次的下一個(gè)位置開始,模式串j再?gòu)?開始
i=i-j+1;
j=0;
}
if(j==strlen(sub))
{
cnt++;
return i-strlen(sub)+1;
}
}
return -1;
}
int main()
{
// s="abcdabefgabefa",sub="abe",返回 5。
char s[20],sub[10];
gets(s);
gets(sub);
printf("%d\n",cnt);
printf("%d\n",index(s,sub));
return 0;
}
如果主串是bbb…bbb,模式串是bbbbc,那每個(gè)串都要比較m次,一共是(n-m+1)*m次。時(shí)間復(fù)雜度很大 = O(n*m),一般簡(jiǎn)單匹配時(shí)候可用此法。
2 Rabin-Karp 算法
算法思路:對(duì)主串的 n-m+1 個(gè)子串分別求哈希值,然后跟模板串的哈希值對(duì)比,如果一樣再逐個(gè)對(duì)比字符串是否一樣。
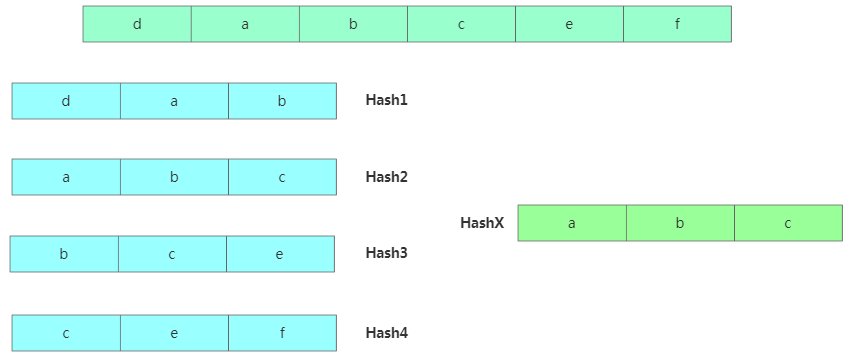
但是中間數(shù)據(jù)的Hash值計(jì)算是可以優(yōu)化的,我們以簡(jiǎn)單的字符串匹配舉例,把a(bǔ)-z映射到0~25上。然后按照26進(jìn)制計(jì)算一個(gè)串的哈希值,比如:

但是你會(huì)發(fā)現(xiàn)相鄰的兩個(gè)子串?dāng)?shù)據(jù)之間是有重疊的,比如
dab跟abc重疊了ab。這樣哈希下一個(gè)數(shù)據(jù)的Hash值其實(shí)可以借鑒下上一個(gè)數(shù)據(jù)的值推導(dǎo)得出:
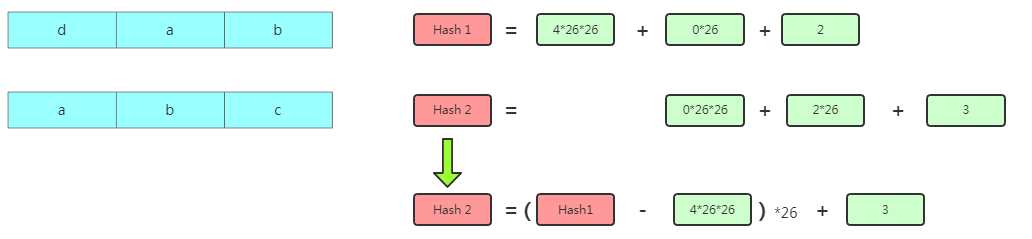
RK算法的時(shí)間復(fù)雜度包含兩部分,第一部分是遍歷所有子串計(jì)算Hash值,時(shí)間復(fù)雜度是O(n)。第二部分是比較哈希值,這部分時(shí)間復(fù)雜度也是O(n)。
這個(gè)算法的核心就是盡量減少哈希值相等的情況下數(shù)據(jù)不一樣從而進(jìn)行的比較,所以哈希算法要盡可能的好,如果你感覺(jué)用123對(duì)應(yīng)字母abc容易碰撞,那用素?cái)?shù)去匹配也是OK的,反正目的是一樣的, 你可以認(rèn)為這是一種取巧的辦法來(lái)處理字符串匹配問(wèn)題。
3 Boyer-Moore 算法。
Boyer Moore算法是一種非常高效的字符串匹配算法,它的性能是著名的 KMP 算法的 3 到 4 倍。它不太好理解,但確是工程中使用最多的字符串匹配算法。以前我們匹配字符串的時(shí)候是一個(gè)個(gè)從前往后挪動(dòng)來(lái)逐次比較,BM 算法核心思想是在模式串中某個(gè)字符與主串不能匹配時(shí),將模式串往后多滑動(dòng)幾位,來(lái)減少不必要的字符比較。

整體而言BM算法還是挺復(fù)雜的相比前面兩種,主要包含
壞字符規(guī)則跟好后綴規(guī)則。
3.1 壞字符規(guī)則
壞字符規(guī)則意思是根據(jù)模式串從后往前匹配,當(dāng)我們發(fā)現(xiàn)某個(gè)字符沒(méi)法匹配的時(shí)候。我們把這個(gè)沒(méi)有匹配的主串中的字符叫作壞字符。
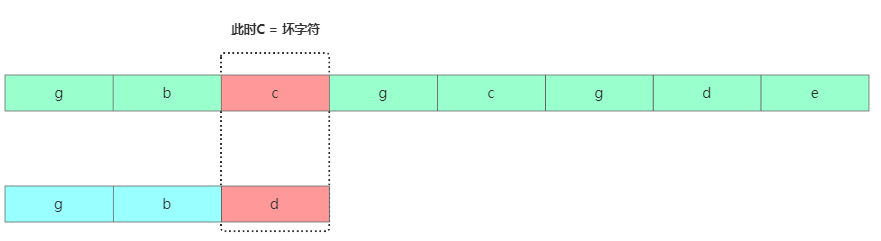
找到壞字符c后,在模式串中繼續(xù)查找發(fā)現(xiàn)c跟模式串任何字符無(wú)法匹配,則可以直接將模式串往后移動(dòng)3位。繼續(xù)從模式串尾部對(duì)比。
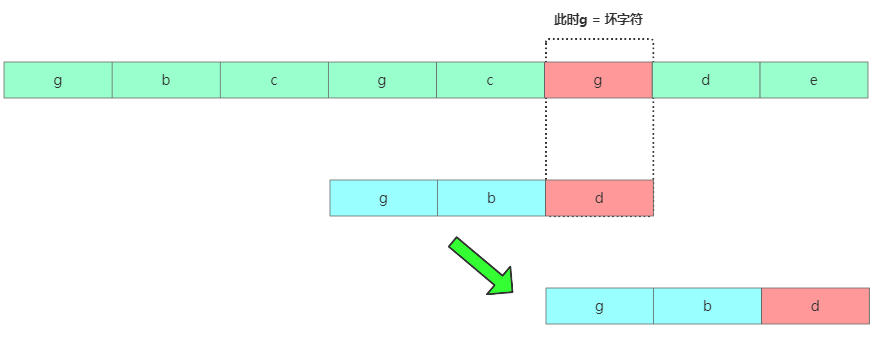
此時(shí)發(fā)現(xiàn)壞字符是g,但在模式串中有個(gè)g存在,不能再往后移動(dòng)3個(gè)了,移動(dòng)的位置是2個(gè)。再繼續(xù)匹配。那有啥規(guī)律呢?
發(fā)送不匹配時(shí),壞字符對(duì)應(yīng)的模式串字符下標(biāo)位置Si,如果壞字符在模式串中存在,取從后往前最先出現(xiàn)的壞字符下標(biāo)記為Xi(取第一個(gè)是怕挪動(dòng)太大咯),如果壞字符在模式串中不存在則Xi = -1。此時(shí)模式串往后移動(dòng)位數(shù)= Si - Xi。
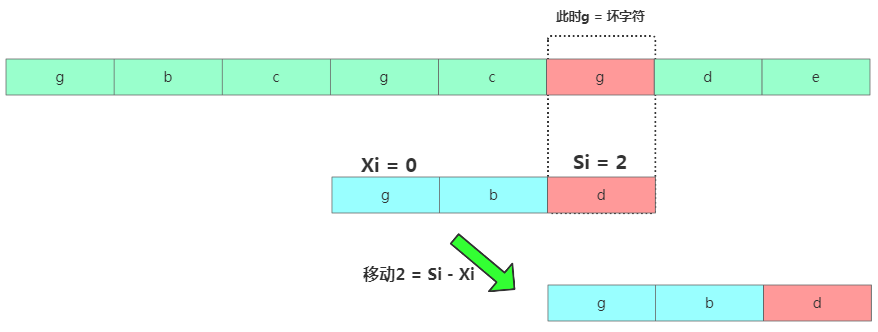
如果碰到極致的主串=cccdcccdcccd,模式串=cccc,那此時(shí)時(shí)間復(fù)雜度是O(n/m)。
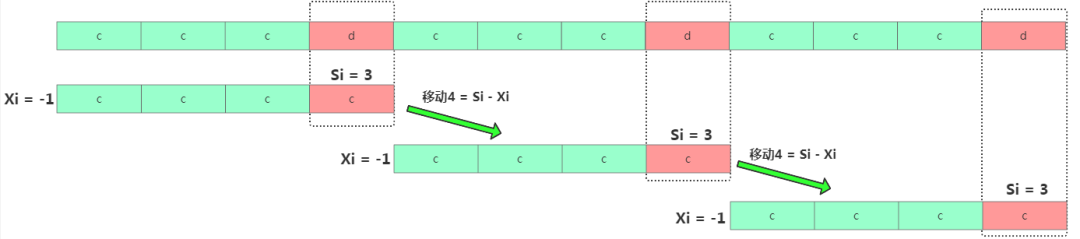
但是不要高興太早!下面這種情況可能導(dǎo)致模式串不往后移動(dòng),反而往前移動(dòng)哦!

所以此時(shí)BM算法還需要用到
好后綴規(guī)則。
3.2 壞字符代碼
為避免每次都拿懷字符從模式串中遍歷查找,此時(shí)用到散列表將模式串中每個(gè)字符及其下標(biāo)存起來(lái),方便迅速查找。
接下來(lái)說(shuō)下散列表規(guī)則,比如一個(gè)字符是一個(gè)字節(jié),用大小為256的數(shù)組記錄每個(gè)字符在模式串出現(xiàn)位置,數(shù)組中存儲(chǔ)的是模式串出現(xiàn)的位置,數(shù)組下表是字符對(duì)應(yīng)的ASCII值。
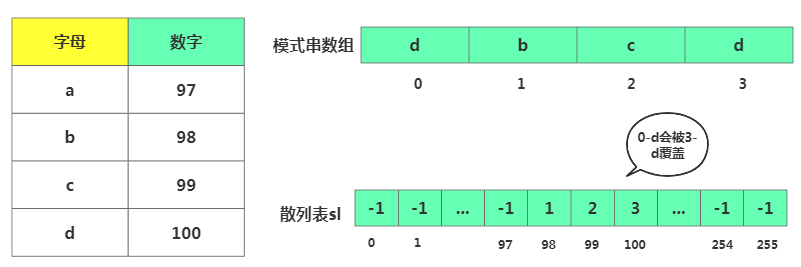
// 全局變量 SIZE
private static final int SIZE = 256;
// b=模式串?dāng)?shù)組,m是模式串?dāng)?shù)組長(zhǎng)度,sl是哈希表,默認(rèn)-1
private void generateBC(char[] b, int m, int[] sl) {
for (int i = 0; i < SIZE; i++) {
sl[i] = -1; // 初始化sl
}
for (int i = 0; i < m; ++i) {
int ascii = (int)b[i];
sl[ascii] = i;
}
}
接下來(lái)先不考慮好后綴規(guī)則跟壞字符的負(fù)數(shù)情況,先大致寫出 BM 算法代碼。
public int bm(char[] a, int n, char[] b, int m) {
// 記錄模式串中每個(gè)字符最后出現(xiàn)的位置
int[] sl = new int[SIZE];
// 構(gòu)建壞字符哈希表
generateBC(b, m, sl);
// i表示主串與模式串對(duì)齊的第一個(gè)字符
int i = 0;
while (i <= n - m) {
int j;
for (j = m - 1; j >= 0; j--) {
if (a[i+j] != b[j]) break;
}
if (j < 0) {
// 匹配成功,返回主串與模式串第一個(gè)匹配的字符的位置
return i;
}
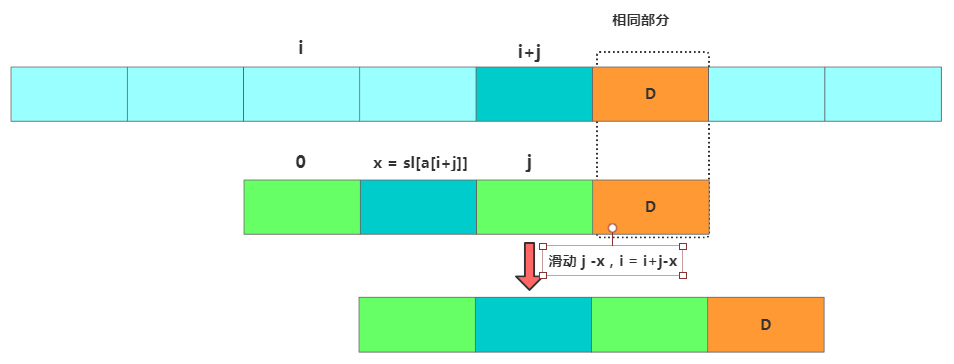
//將模式串往后滑動(dòng)j-bc[(int)a[i+j]]位
i = i + (j - sl[(int)a[i+j]]);
}
return -1;
}
3.3 好后綴規(guī)則
好后綴跟壞后綴道理類似,從后往前匹配,直到遇到不匹配的字符x,那主串x之前的就叫好后綴。
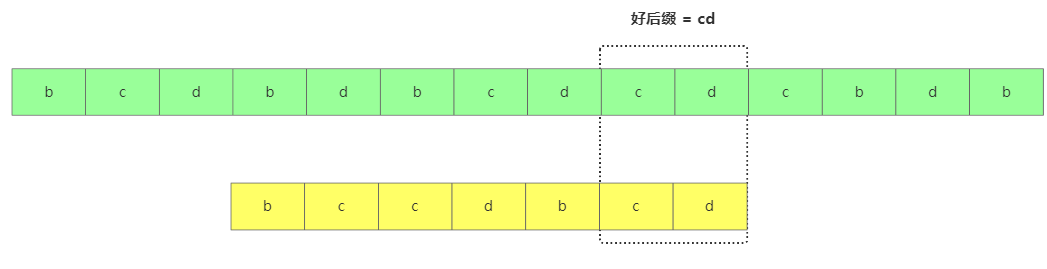
此時(shí)移動(dòng)的規(guī)則如下:
如果好后綴在模式串中找到了,用x框起來(lái),然后將x框跟好后綴對(duì)齊繼續(xù)匹配。
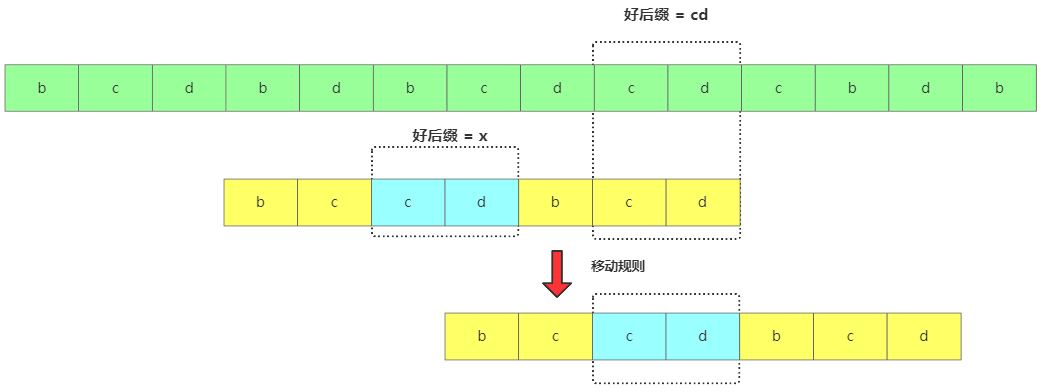
找到了移動(dòng)規(guī)則 找不到的時(shí)候,如果直接移動(dòng)長(zhǎng)度是模式串m位,那極有可能過(guò)度了!而過(guò)度移動(dòng)存在的原因就是,比如你找了好后綴u,u在模式串中整體沒(méi)找到,但是u的子串d是可以跟模式串匹配上的啊。
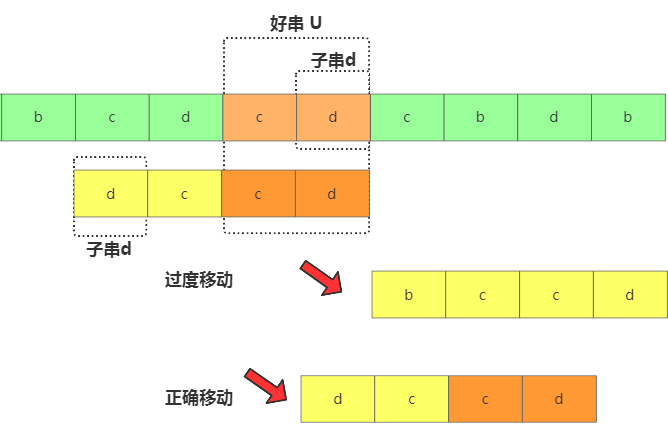
過(guò)度移動(dòng)
所以此時(shí)還要看好后綴的后綴子串是否跟模式串中的前綴子串匹配,從好后綴串的后后綴子串中找個(gè)最長(zhǎng)能跟模式串的前綴子串匹配的然后滑動(dòng)到一起,比如上面的d。
然后分別計(jì)算壞字符往后滑動(dòng)位數(shù)跟好后綴往后滑動(dòng)此時(shí),兩者取其大作為模式串往后滑動(dòng)位數(shù),這種情況下還可以避免壞字符的負(fù)數(shù)情況。
3.4 好后綴代碼
好后綴的核心其實(shí)就在于兩點(diǎn):
在模式串中,查找跟好后綴匹配的另一個(gè)子串。
在好后綴的后綴子串中,查找最長(zhǎng)的、能跟模式串前綴子串匹配的后綴子串。
3.4.1 預(yù)處理工作
上面兩個(gè)核心點(diǎn)可以在代碼層面用暴力解決,但太耗時(shí)!我們可以在匹配前通過(guò)預(yù)處理模式串,預(yù)先計(jì)算好模式串的每個(gè)后綴子串,對(duì)應(yīng)的另一個(gè)可匹配子串的位置。
先看如何表示模式串中不同的后綴子串,因?yàn)楹缶Y子串的最后個(gè)字符下標(biāo)為m-1,我們只需記錄后綴子串長(zhǎng)度即可,通過(guò)長(zhǎng)度可以確定一個(gè)唯一的后綴子串。
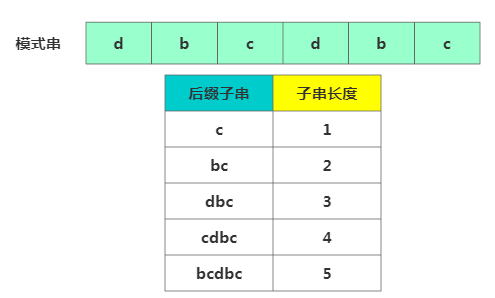
再引入關(guān)鍵的變量
suffix數(shù)組。suffix 數(shù)組的index表示后綴子串的長(zhǎng)度。下標(biāo)對(duì)應(yīng)的數(shù)組值存儲(chǔ)的是
好后綴在模式串中匹配的起始下標(biāo)值:
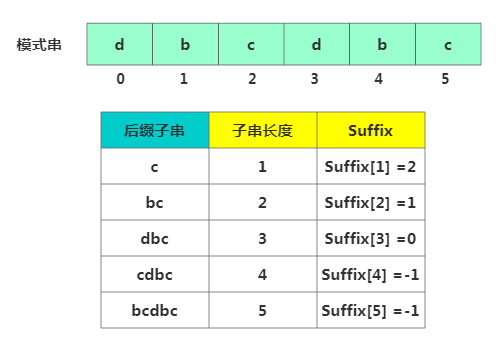
比如此處后綴子串c在模式串中另一個(gè)匹配開始位置為2, 后綴子串bc在模式串中另一個(gè)匹配開始位置為1 后綴子串dbc在模式串中另一個(gè)匹配開始位置為0, 后綴子串cdbc在模式串中只出現(xiàn)了一次,所以為-1。
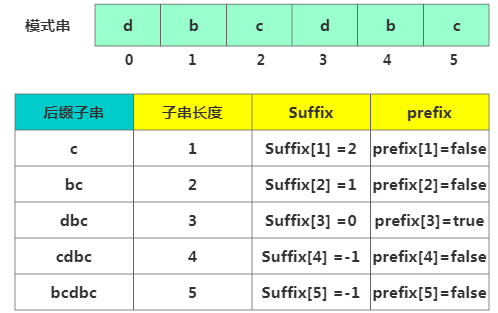
這里需注意,我們不僅要在模式串中查找跟好后綴匹配的另一個(gè)子串,還要在好后綴的后綴子串中查找最長(zhǎng)的能跟模式串前綴子串匹配的后綴子串。比如下面:
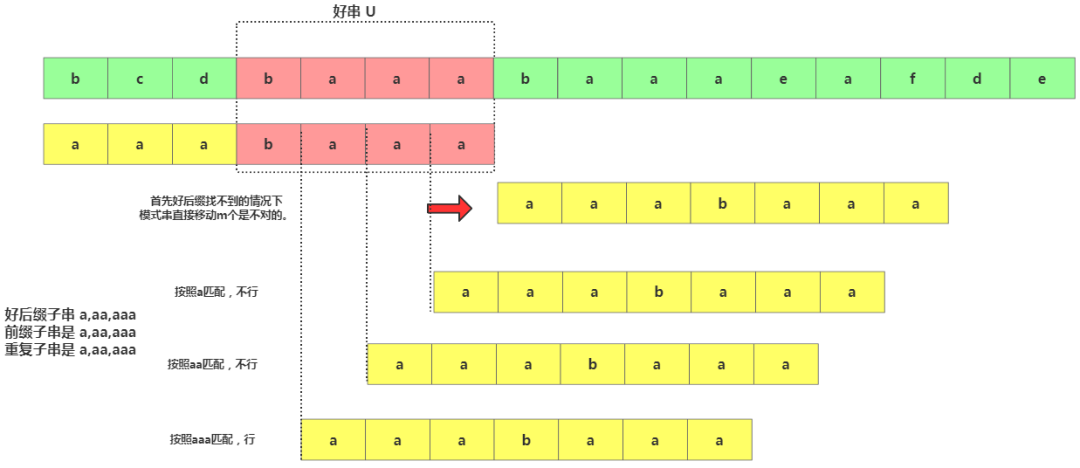
用suffix只能查找跟好后綴匹配的另一個(gè)子串。但還需要個(gè) boolean 類型的prefix數(shù)組來(lái)記錄模式串的后綴子串是否能匹配模式串的前綴子串。
接下來(lái)重點(diǎn)看下如何填充suffix跟prefix數(shù)組,拿下標(biāo)從 0 到 i 的子串與整個(gè)模式串,求公共后綴子串,其中i=[0,m-2]。如果公共后綴子串的長(zhǎng)度是 k,就suffix[k]=j,其中 j 表示公共后綴子串的起始下標(biāo)。如果 j = 0,說(shuō)明公共后綴子串也是模式串的前綴子串,此時(shí) prefix[k]=true。
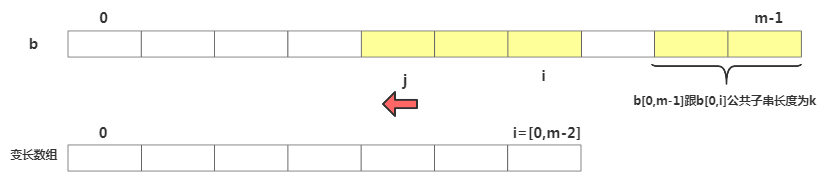
// b=模式串,m=模式串長(zhǎng)度,suffix,prefix 數(shù)組 如上定義
private void generateGS(char[] b, int m, int[] suffix, boolean[] prefix) {
//初始化
for (int i = 0; i < m; i++) {
suffix[i] = -1;
prefix[i] = false;
}
// b[0, i]
for (int i = 0; i < m - 1; i++) {
int j = i;
// 公共后綴子串長(zhǎng)度
int k = 0;
// 與b[0, m-1]求公共后綴子串,并且會(huì)有覆蓋現(xiàn)象產(chǎn)生。
while (j >= 0 && b[j] == b[m-1-k]) {
--j;
++k;
//j+1表示公共后綴子串在b[0, i]中的起始下標(biāo)
suffix[k] = j+1;
}
//如果公共后綴子串也是模式串的前綴子串
if (j == -1) prefix[k] = true;
}
}
3.4.2 正式代碼
有了suffix跟prefix數(shù)組后,看下移動(dòng)規(guī)則。假設(shè)好后綴串長(zhǎng)度=k,如果k != 0,說(shuō)明有好后綴,接下來(lái)通過(guò)suffix[k]的值來(lái)判斷如何移動(dòng)。
suffix[k] != -1,不等于時(shí)說(shuō)明匹配上了,模式串后移 j-suffix[k]+1 位,其中 j 表示壞字符對(duì)應(yīng)的模式串中的字符下標(biāo)。
suffix[k] = -1,等于時(shí)說(shuō)明好后綴沒(méi)匹配上,那就看下子串的匹配情況,好后綴的后綴子串長(zhǎng)度是 b[r, m-1],其中 r = [j+2,m-1],后綴子串長(zhǎng)度 k=m-r,如果 prefix[k] = true,說(shuō)明長(zhǎng)度為 k 的后綴子串有可匹配的前綴子串,這樣我們可以把模式串后移 r 位。
如果都沒(méi)匹配上,那就直接將模式串后移m位。
// a跟n 分別表示主串跟主串長(zhǎng)度。
// b跟m 分別表示模式串跟模式串長(zhǎng)度。
public int bm(char[] a, int n, char[] b, int m) {
// 用來(lái)記錄模式串中每個(gè)字符最后出現(xiàn)的位置
int[] sl = new int[SIZE];
// 構(gòu)建壞字符哈希表
generateBC(b, m, sl);
int[] suffix = new int[m];
boolean[] prefix = new boolean[m];
// 構(gòu)建 suffix 跟 prefix 數(shù)組
generateGS(b, m, suffix, prefix);
int i = 0; // j表示主串與模式串匹配的第一個(gè)字符
while (i <= n - m) {
int j;
// 模式串從后往前匹配
for (j = m - 1; j >= 0; --j) {
// 壞字符對(duì)應(yīng)模式串中的下標(biāo)是j
if (a[i+j] != b[j]) break;
}
if (j < 0) {
// 匹配OK ,返回主串與模式串第一個(gè)匹配的字符的位置
return i;
}
// 壞字符計(jì)算所得需移動(dòng)長(zhǎng)度
int x = j - sl[(int)a[i+j]];
int y = 0;
// j < m-1 說(shuō)明有好的匹配上了
if (j < m-1) {
y = moveByGS(j, m, suffix, prefix);
}
i = i + Math.max(x, y);
}
return -1;
}
// j = 壞字符對(duì)應(yīng)的模式串中的字符下標(biāo)
// m = 模式串長(zhǎng)度
private int moveByGS(int j, int m, int[] suffix, boolean[] prefix) {
// 好后綴長(zhǎng)度
int k = m - 1 - j;
if (suffix[k] != -1) {
// 好后綴可以匹配上,返回需移動(dòng)長(zhǎng)度
return j - suffix[k] + 1;
}
// 有匹配到好后綴子串的模式串前綴子串
for (int r = j+2; r <= m-1; ++r) {
if (prefix[m-r] == true) {
return r;
}
}
// 沒(méi)找到直接 移動(dòng)最大值
return m;
}
3.5 復(fù)雜度分析
整個(gè)BM算法用到了額外的 sl、suffix、prefix三個(gè)數(shù)組,其中sl數(shù)組大小跟字符集大小有關(guān),suffix 數(shù)組和 prefix 數(shù)組的大小跟模式串長(zhǎng)度 m 有關(guān)。如果處理字符集很大的字符串匹配問(wèn)題,bc 數(shù)組對(duì)內(nèi)存的消耗就會(huì)比較多。
因?yàn)楹煤缶Y和壞字符規(guī)則是獨(dú)立的,如果我們運(yùn)行的環(huán)境對(duì)內(nèi)存要求苛刻,可以只使用好后綴規(guī)則,不使用壞字符規(guī)則,這樣就可以避免 bc 數(shù)組過(guò)多的內(nèi)存消耗。不過(guò),單純使用好后綴規(guī)則的 BM 算法效率就會(huì)下降一些了。
BM 算法的時(shí)間復(fù)雜度分析起來(lái)是非常復(fù)雜,一般在3n~5n之間。
4 KMP 算法
KMP算法跟BM算法類似,從前往后匹配,把能匹配上的叫好前綴,不能匹配上的叫壞字符。
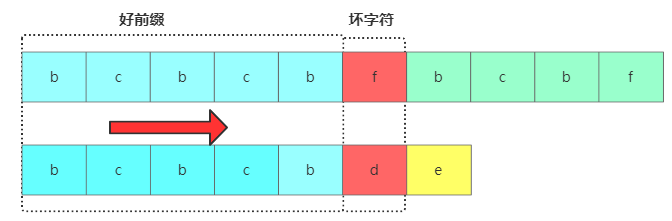
遇到壞字符后就要進(jìn)行主串好前綴后綴子串跟模式串的前綴子串進(jìn)行對(duì)比,問(wèn)題是對(duì)于已經(jīng)比對(duì)過(guò)的好前綴,能否找到一種規(guī)律,將模式串一次性滑動(dòng)很多位?
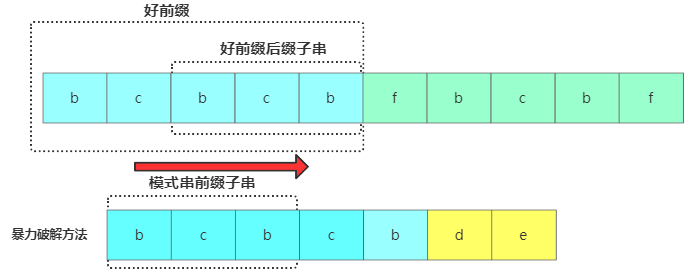
思路是將主串中好前綴的后綴子串和模式串中好前綴的前綴子串進(jìn)行對(duì)比,獲取模式串中最大可以匹配的前綴子串。一般把好前綴的所有后綴子串中,最長(zhǎng)的可匹配前綴子串的那個(gè)后綴子串,叫作最長(zhǎng)可匹配后綴子串。對(duì)應(yīng)的前綴子串,叫作最長(zhǎng)可匹配前綴子串。假如現(xiàn)在最長(zhǎng)可匹配后綴子串 = u,最長(zhǎng)可匹配前綴子串 = v,獲得u跟v的長(zhǎng)度為k,此時(shí)在主串中壞字符位置為i,模式串中為j,接下來(lái)將模式串后移j-k位,然后將待比較的模式串位置j = j-k進(jìn)行比較。
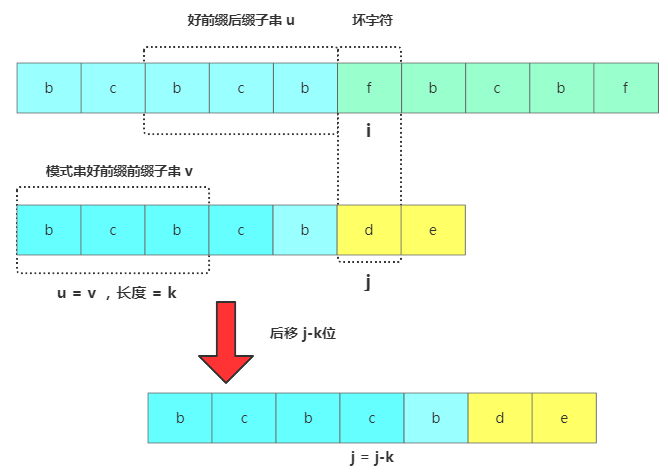
4.1 Next 數(shù)組存在意義
那最長(zhǎng)可匹配前綴跟后綴我們用模式串就可以求解了。仿照BM算法,預(yù)先計(jì)算好就行。在KMP算法中提前構(gòu)造個(gè)next數(shù)組。其中next數(shù)組的下標(biāo)用來(lái)存儲(chǔ)前綴子串最后一個(gè)數(shù)據(jù)的index,對(duì)應(yīng)的value保存的是這個(gè)字符串的后綴子串集合跟前綴子串集合的交集。
干說(shuō)可能不太好理解,我們以"abababca"為例。它的部分匹配表(Partial Match Table)數(shù)組如下:
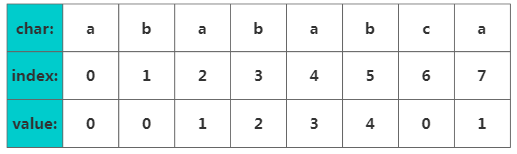
接下來(lái)對(duì)value值的獲取進(jìn)行解釋,如果字符串A和B,存在A=BS,其中S是任意的非空字符串,那就稱B為A的前綴。例如”what”的前綴包括{"w","wh","wha"},我們把所有前綴組成的字符串的前綴集合。同樣可以定義后綴A=SB, 其中S是任意的非空字符串,那就稱B為A的后綴,例如"Potter"的后綴包括{"otter", "tter", "ter", "er", "r"},然后把所有后綴組成字符串的后綴集合。要注意字符串本身并不是自己的后綴。
PMT數(shù)組中的值是字符串的前綴集合與后綴集合的交集中最長(zhǎng)元素的長(zhǎng)度。例如,對(duì)于"aba",它的前綴集合為{"a", "ab"},后綴集合為{"ba", "a"}。兩個(gè)集合的交集為{"a"},那么長(zhǎng)度最長(zhǎng)的元素就是字符串"a"了,長(zhǎng)度為1,所以"aba"的Next數(shù)組value = 1,同理對(duì)于"ababa",它的前綴集合為{"a", "ab", "aba", "abab"},它的后綴集合為{"baba", "aba", "ba", "a"}, 兩個(gè)集合的交集為{"a", "aba"},其中最長(zhǎng)的元素為"aba",長(zhǎng)度為3。
我們以主串"ababababca"中查找模式串"abababca"為例,如果在j處字符不匹配了,那在模式串[0,j-1]的數(shù)據(jù)串"ababab"中,前綴集合跟后綴集合的交集最大值就是長(zhǎng)度為4的"abab"。
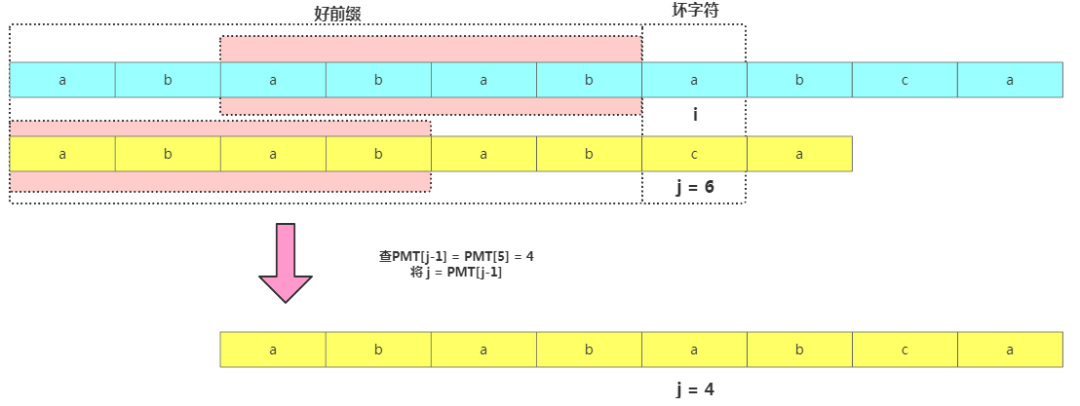
基于此就可以使用PMT加速字符串的查找了。我們看到如果是在
j位失配,那么影響j 指針回溯的位置的其實(shí)是第 j?1 位的 PMT 值,但是編程中為了方便一般不直接使用PMT數(shù)組而是使用Next數(shù)組,Next數(shù)組的value其實(shí)就是存儲(chǔ)的這個(gè)前綴的最長(zhǎng)可以匹配前綴子串的結(jié)尾字符下標(biāo),其中如果匹配不到用-1代替。
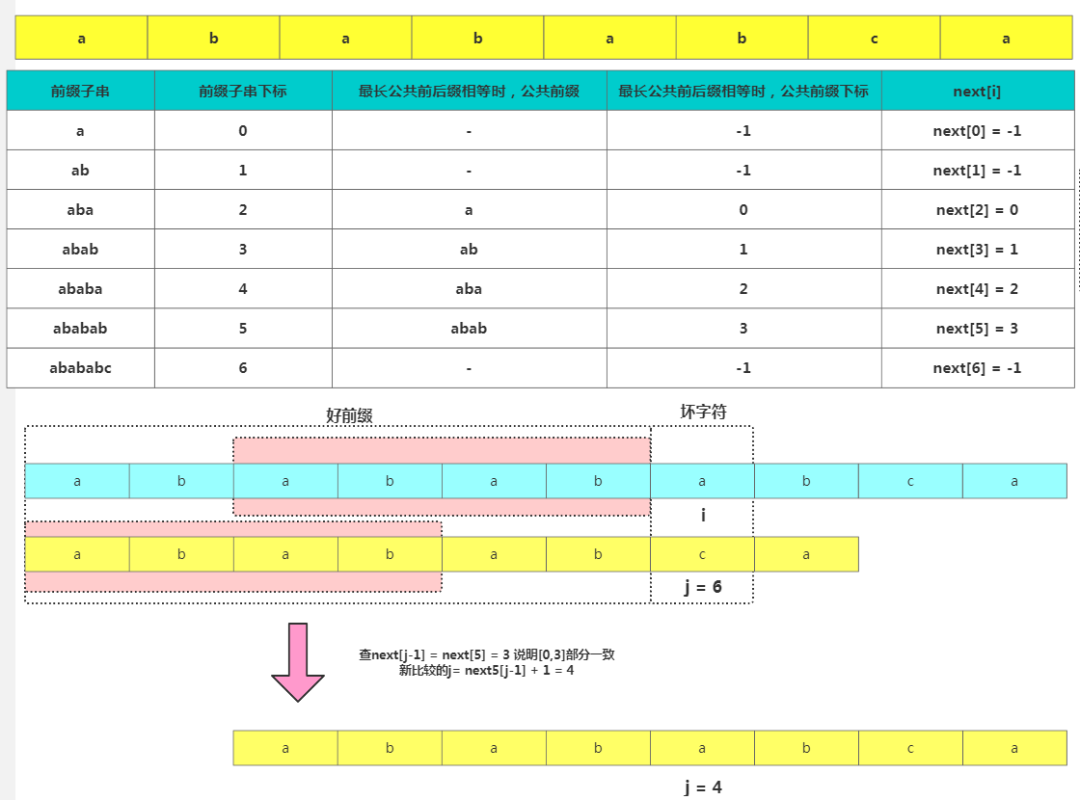
4.2 KMP 匹配代碼
// a = 主串,n=主串長(zhǎng)度。b = 模式串,m = 模式串長(zhǎng)度
public static int kmp(char[] a, int n, char[] b, int m) {
int[] next = getNexts(b, m);
int j = 0;
for (int i = 0; i < n; ++i) {
while (j > 0 && a[i] != b[j]) {
j = next[j - 1] + 1; // 發(fā)現(xiàn)不一樣則 保持i 不變 j進(jìn)行移動(dòng)
}
if (a[i] == b[j]) {
++j;
}
if (j == m) { // 找到匹配模式串的了
return i - m + 1;
}
}
return -1;
}
至此你會(huì)發(fā)現(xiàn)只要搞明白了PMT存在的意義,然后順著思路推Next數(shù)組即可。
4.3 Next 數(shù)組求解
當(dāng)要計(jì)算next[i]時(shí),前面計(jì)算過(guò)的next[0~i-1]是否可以被用來(lái)快速推導(dǎo)出next[i]呢?
情況一:如果next[i-1] = k-1,那此時(shí)b[0,i-1]的最長(zhǎng)可匹配前綴子串是b[0,k-1],如果b[0,i-1]的下個(gè)字符b[i]跟b[0,k-1]的下個(gè)字符b[k]相等,那next[i] = k。

情況二:假設(shè)b[0,i]最長(zhǎng)可用后綴子串是b[r,i],那b[r,i-1]肯定是b[0,i-1]的可匹配后綴子串,但不一定是最長(zhǎng)可匹配后綴子串。比如字符串b = "dexdecdexdex",此時(shí)最長(zhǎng)可匹配后綴子串是"dex",b去掉最后的'x'成為B,此時(shí)雖然"de"是B的可匹配后綴子串,但"dexde"才是最長(zhǎng)后綴子串!也就是說(shuō)b[0, i-1]最長(zhǎng)可匹配后綴子串對(duì)應(yīng)的模式串的前綴子串的下一個(gè)字符并不等于 b[i]。
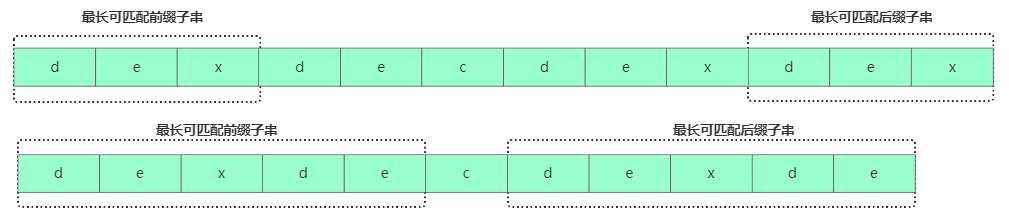
那此時(shí)看下b[0,i-1]的
次長(zhǎng)可匹配后綴子串b[x,i-1]對(duì)應(yīng)的可匹配前綴子串b[0,i-1-x] 的下個(gè)字符b[i-x] 是否等于b[i],相等那b[0,i]的最長(zhǎng)可匹配后綴子串是b[x,i]。
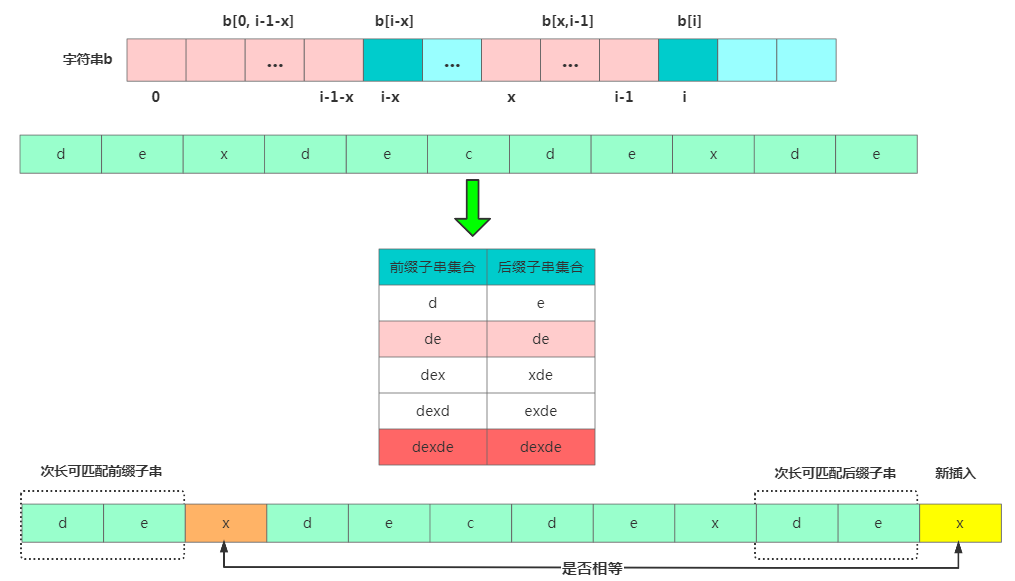
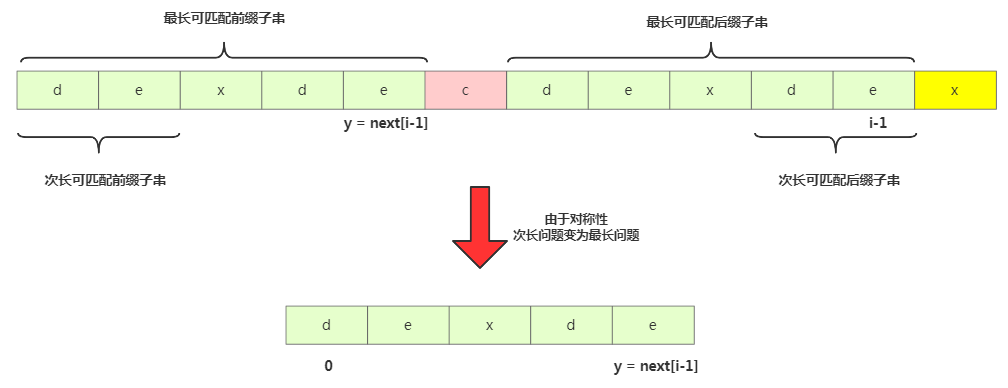
那我們來(lái)求 b[0, i-1]的次長(zhǎng)可匹配后綴子串呢?次長(zhǎng)可匹配后綴子串一定被包含在最長(zhǎng)可匹配后綴子串中,而最長(zhǎng)可匹配后綴子串又對(duì)應(yīng)最長(zhǎng)可匹配前綴子串 b[0, y]。此時(shí)查找 b[0, i-1]的次長(zhǎng)可匹配后綴子串變成了查找b[0, y]的最長(zhǎng)匹配后綴子串的問(wèn)題。
按此思路考察完所有的 b[0, i-1]的可匹配后綴子串 b[y, i-1],直到找到一個(gè)可匹配的后綴子串,它對(duì)應(yīng)的前綴子串的下一個(gè)字符等于 b[i],那這個(gè) b[y, i]就是 b[0, i]的最長(zhǎng)可匹配后綴子串。
// b = 模式串,m = 模式串的長(zhǎng)度
private static int[] getNexts(char[] b, int m) {
int[] next = new int[m];
next[0] = -1;
int k = -1;
for (int i = 1; i < m; ++i) {
while (k != -1 && b[k + 1] != b[i]) {
k = next[k];
// 因?yàn)榍耙粋€(gè)的最長(zhǎng)串的下一個(gè)字符不與最后一個(gè)相等,需要找前一個(gè)的次長(zhǎng)串,
// 問(wèn)題就變成了求0到next(k)的最長(zhǎng)串,如果下個(gè)字符與最后一個(gè)不等,
// 繼續(xù)求次長(zhǎng)串,也就是下一個(gè)next(k),直到找到,或者完全沒(méi)有
// 最好結(jié)合前面的圖來(lái)看
}
if (b[k + 1] == b[i]) {
++k; // 字符串相等則看下一個(gè)
}
next[i] = k; // 數(shù)組賦值
}
return next;
}
KMP空間復(fù)雜度:該算法只需要一個(gè)額外的 next 數(shù)組,數(shù)組的大小跟模式串相同。所以空間復(fù)雜度是 O(m),m 表示模式串的長(zhǎng)度。
KMP時(shí)間復(fù)雜度:next 數(shù)組計(jì)算的時(shí)間復(fù)雜度是 O(m) + 匹配時(shí)候時(shí)間復(fù)雜度是 O(n) = O(m+n)
至此,常見的字符串匹配算法正式講解完畢,其實(shí)前面說(shuō)的都是一個(gè)主串,一個(gè)模式串。如果感興趣你也可以看下AC自動(dòng)機(jī),該算法可實(shí)現(xiàn)遍歷一次主串同時(shí)匹配多個(gè)模式串,屬于KMP的升級(jí)版,在平常字符串匹配的時(shí),用途廣泛。本文核心思路借鑒極客時(shí)間小爭(zhēng)哥的數(shù)據(jù)結(jié)構(gòu)跟算法課程,課程質(zhì)量相當(dāng)高,作為自來(lái)水推薦一波,有想購(gòu)買的私聊我,有優(yōu)惠哦。
5 參考
極客時(shí)間KMP:https://time.geekbang.org/column/article/71845
知乎KMP:https://www.zhihu.com/question/21923021
袁廚KMP:https://t.1yb.co/i95V
-End-
最近有一些小伙伴,讓我?guī)兔φ乙恍?nbsp;面試題 資料,于是我翻遍了收藏的 5T 資料后,匯總整理出來(lái),可以說(shuō)是程序員面試必備!所有資料都整理到網(wǎng)盤了,歡迎下載!
面試題】即可獲取
