CNN常用卷積方法一覽
這篇文章的主題是卷積(Convlution)。想必熟悉CNN的你一定對卷積很熟悉了,或許也聽過用過深度學(xué)習(xí)可分離卷積、轉(zhuǎn)置卷積等概念和方法。那么目前為止,深度學(xué)習(xí)中都有哪些典型的卷積方式?本篇筆者就和大家一起來總結(jié)一下這些功能強(qiáng)大的卷積。本文的目錄如下:
卷積的本質(zhì)
常規(guī)卷積
單通道卷積
多通道卷積
3D卷積
轉(zhuǎn)置卷積
1x1卷積
深度可分離卷積
空洞卷積
卷積的本質(zhì)
在具體介紹各種卷積之前,我們有必要再來回顧一下卷積的真實含義,從數(shù)學(xué)和圖像處理應(yīng)用的意義上來看一下卷積到底是什么操作。目前大多數(shù)深度學(xué)習(xí)教程很少對卷積的含義進(jìn)行細(xì)述,大部分只是對圖像的卷積操作進(jìn)行了闡述。以至于卷積的數(shù)學(xué)意義和物理意義很多人并不是很清楚,究竟為什么要這樣設(shè)計,這么設(shè)計的原因如何。
追本溯源,我們先回到數(shù)學(xué)教科書中來看卷積。在泛函分析中,卷積也叫旋積或者褶積,是一種通過兩個函數(shù)x(t)和h(t)生成的數(shù)學(xué)算子。其計算公式如下:
連續(xù)形式:
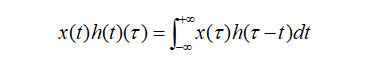
離散形式:
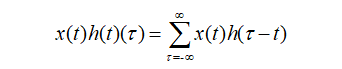
公式寫的很清楚了,兩個函數(shù)的卷積就是先將一個函數(shù)進(jìn)行翻轉(zhuǎn)(Reverse),然后再做一個平移(Shift),這便是"卷"的含義。而"積"就是將平移后的兩個函數(shù)對應(yīng)元素相乘求和。所以卷積本質(zhì)上就是一個Reverse-Shift-Weighted Summation的操作。
數(shù)無形時少直觀。我們用兩個函數(shù)圖像來直觀的展示卷積過程和含義。兩個函數(shù)x(t)和h(t)的圖像如下圖所示:
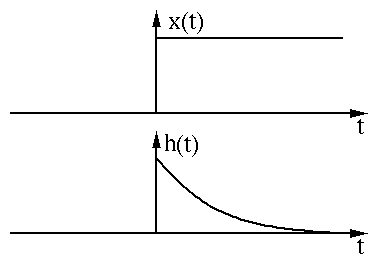
我們先對其中一個函數(shù)h(t)進(jìn)行翻轉(zhuǎn)(Reverse)操作:
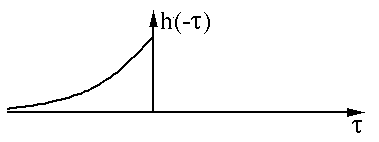
然后進(jìn)行平移(Shift):
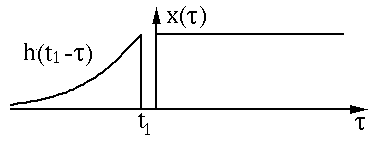
以上過程是為"卷"。然后是"積"的過程,因為是連續(xù)函數(shù),這里相乘求和為積分形式,圖中綠色部分即為相乘求和部分。
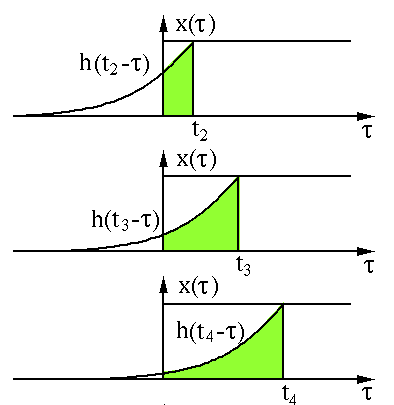
圖像來自:
http://fourier.eng.hmc.edu/e161/lectures/convolution/index.html
那么為什么要卷積?直接元素相乘不好嗎?就圖像的卷積操作而言,筆者認(rèn)為卷積能夠更好提取區(qū)域特征,使用不同大小的卷積算子能夠提取圖像各個尺度的特征。卷積在信號處理、圖像處理等領(lǐng)域有著廣泛的應(yīng)用。當(dāng)然,之于深度學(xué)習(xí)而言,卷積神經(jīng)網(wǎng)絡(luò)主要用于圖像領(lǐng)域。回顧了卷積的本質(zhì)之后,我們再來一一梳理CNN中典型的卷積操作。
常規(guī)卷積
我們從最原始的圖像卷積操作開始。因為圖像有單通道圖像(灰度圖)和多通道圖(RGB圖),所以對應(yīng)常規(guī)卷積方式可以分為單通道卷積和多通道卷積。二者本質(zhì)上并無太大差異,無非對每個通道都要進(jìn)行卷積而已。先來看單通道卷積。
在單通道卷積中,針對圖像的像素矩陣,卷積操作就是用一個卷積核來逐行逐列的掃描像素矩陣,并與像素矩陣做元素相乘,以此得到新的像素矩陣。其中卷積核也叫過濾器或者濾波器,濾波器在輸入像素矩陣上掃過的面積稱之為感受野。假設(shè)輸入圖像維度為n*n*c,濾波器維度為f*f*n,卷積步長為s,padding大小為p,那么輸出維度可以計算為:
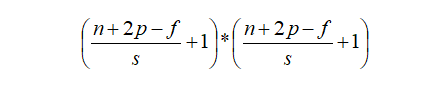
一個標(biāo)準(zhǔn)的單通道卷積如下圖所示:
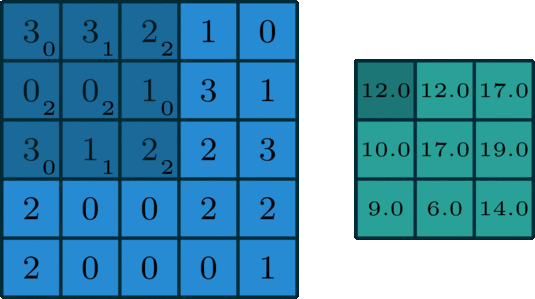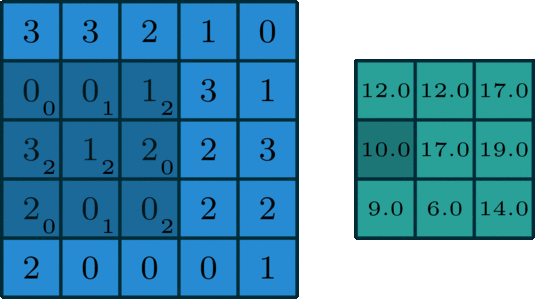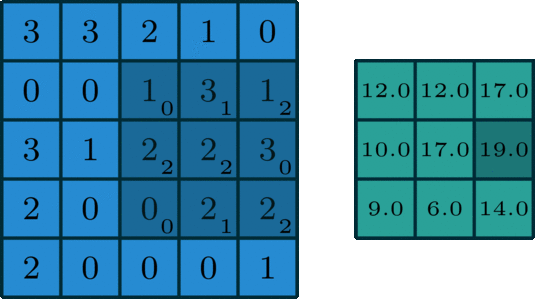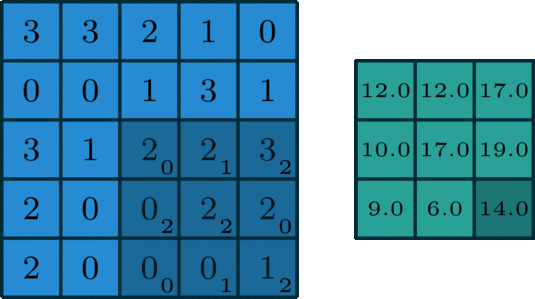
圖像來自:
https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1
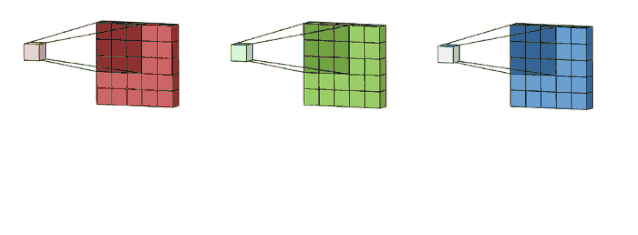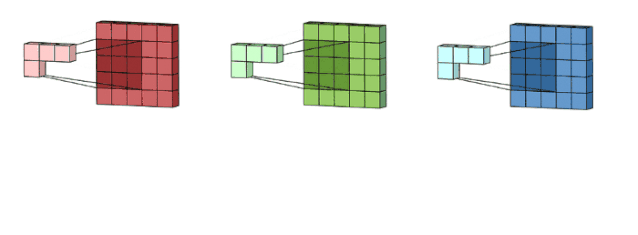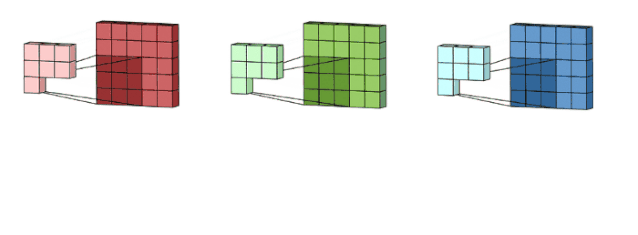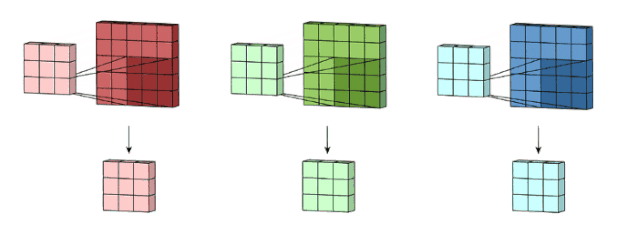
我們這里沒有加入padding和stride等卷積要素,僅僅是為了說明一般的卷積過程。那么如何理解多通道(3通道)卷積呢?其實也很簡單。比如說我們現(xiàn)在有一個5*5*3的RGB 3通道圖像,我們可以將其看成是3張5*5圖像的堆疊,這時候我們把原先的單通道濾波器*3,用3個濾波器分別對著三張圖像進(jìn)行卷積,將卷積得到三個特征圖加總起來便是最后結(jié)果。這里強(qiáng)調(diào)一點(diǎn):濾波器的通道數(shù)一定要跟輸入圖像的通道數(shù)一致,不然會漏下某些通道得不到卷積。現(xiàn)在我們用3*3*3的濾波器對5*5*3的輸入進(jìn)行卷積,得到的輸出維度為3*3。這里少了通道數(shù),所以一般我們會用多個3通道濾波器來進(jìn)行卷積,假設(shè)我們這里用了10個3*3*3的濾波器,那最后的輸出便為3*3*10,濾波器的個數(shù)變成了輸出特征圖的通道數(shù)。

圖像來自:
https://towardsdatascience.com/a-comprehensive-introduction-to-different-types-of-convolutions-in-deep-learning-669281e58215
我們也可以從3D的角度來理解多通道卷積:我們可以將3*3*3的濾波器想象為一個三維的立方體,為了計算立方體濾波器在輸入圖像上的卷積操作,我們首先將這個三維的濾波器放到左上角,讓三維濾波器的27個數(shù)依次乘以紅綠藍(lán)三個通道中的像素數(shù)據(jù),即濾波器的前9個數(shù)乘以紅色通道中的數(shù)據(jù),中間9個數(shù)乘以綠色通道中的數(shù)據(jù),最后9個數(shù)乘以藍(lán)色通道中的數(shù)據(jù)。將這些數(shù)據(jù)加總起來,就得到輸出像素的第一個元素值。示意圖如下所示:
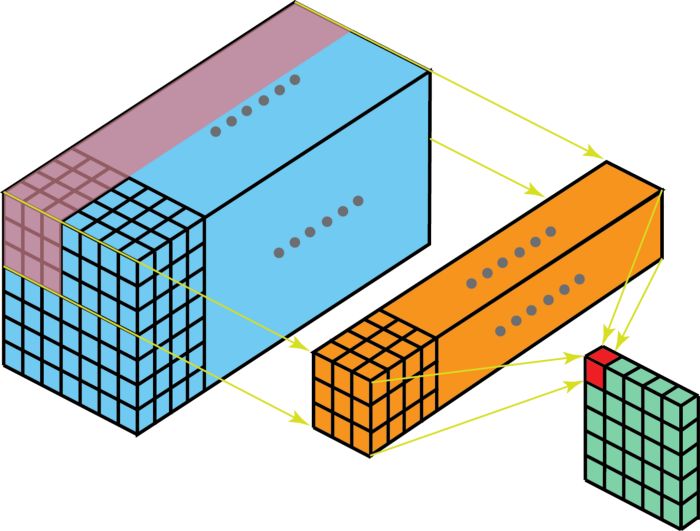
圖像來自:
https://towardsdatascience.com/a-comprehensive-introduction-to-different-types-of-convolutions-in-deep-learning-669281e58215
3D卷積
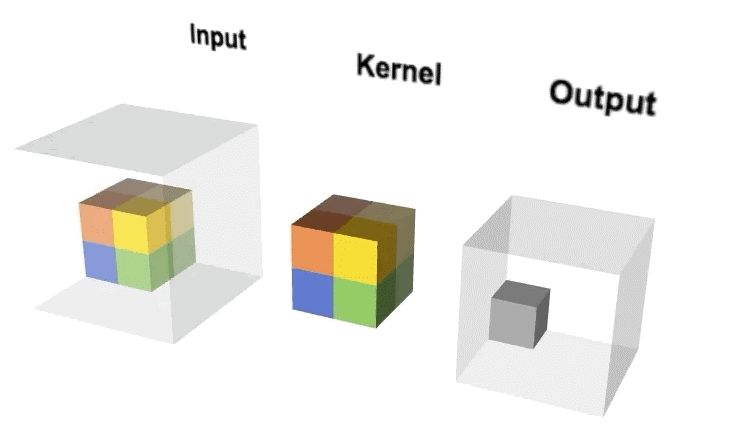
將2D卷積增加一個深度維便可擴(kuò)展為3D卷積。輸入圖像是3維的,濾波器也是3維的,對應(yīng)的卷積輸出同樣是3維的。操作示意圖如下:
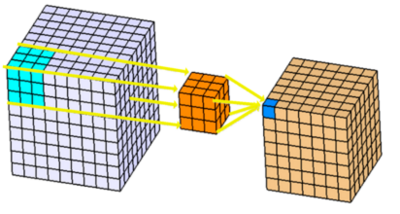
可以想象一下3D卷積的動態(tài)圖。用一個2*2*2的3D濾波器對一個4*4*4的輸入圖像進(jìn)行3D卷積,可以得到一個3*3*3的輸出。
我們可以把2D卷積的計算輸出公式進(jìn)行擴(kuò)展,可以得到3D卷積的輸出維度計算公式。假設(shè)輸入圖像大小為a1*a2*a3,通道數(shù)為c,過濾器大小為f*f*f*c,濾波器數(shù)量為n,則輸出維度可以表示為:
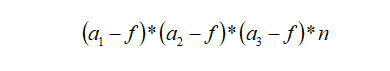
3D卷積在醫(yī)學(xué)影像數(shù)據(jù)、視頻分類等領(lǐng)域都有著較為廣泛的應(yīng)用。相較于2D卷積,3D卷積的一個特點(diǎn)就是卷積計算量巨大,對計算資源要求相對較高。
轉(zhuǎn)置卷積
轉(zhuǎn)置卷積(Transposed Convolution)也叫解卷積(Deconvolution),有些人也將其稱為反卷積,但這個叫法并不太準(zhǔn)確。大家都知道,在常規(guī)卷積時,我們每次得到的卷積特征圖尺寸是越來越小的。但在圖像分割等領(lǐng)域,我們是需要逐步恢復(fù)輸入時的尺寸的。如果把常規(guī)卷積時的特征圖不斷變小叫做下采樣,那么通過轉(zhuǎn)置卷積來恢復(fù)分辨率的操作可以稱作上采樣。
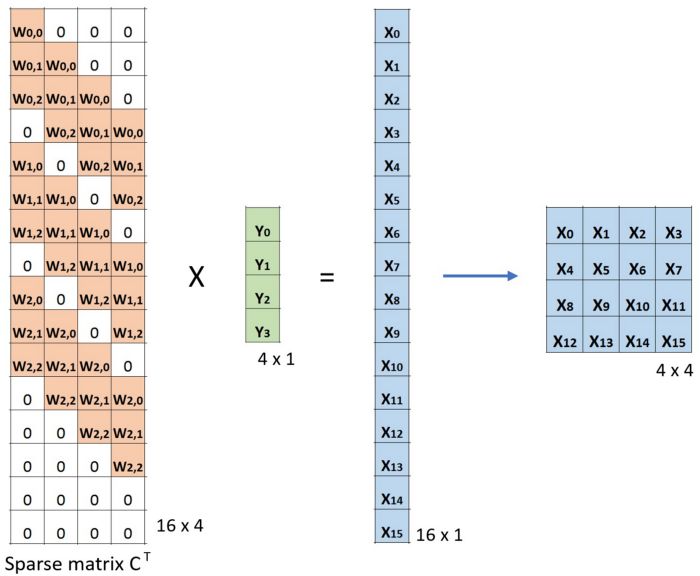
本質(zhì)上來說,轉(zhuǎn)置卷積跟常規(guī)卷積并無區(qū)別。不同之處在于先按照一定的比例進(jìn)行padding來擴(kuò)大輸入尺寸,然后把常規(guī)卷積中的卷積核進(jìn)行轉(zhuǎn)置,再按常規(guī)卷積方法進(jìn)行卷積就是轉(zhuǎn)置卷積。假設(shè)輸入圖像矩陣為X,卷積核矩陣為C,常規(guī)卷積的輸出為Y,則有:
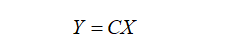
兩邊同時乘以卷積核的轉(zhuǎn)置CT,這個公式便是轉(zhuǎn)置卷積的輸入輸出計算。
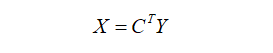
假設(shè)輸入大小為4*4,濾波器大小為3*3,常規(guī)卷積下輸出為2*2,為了演示轉(zhuǎn)置卷積,我們將濾波器矩陣進(jìn)行稀疏化處理為4*16,將輸入矩陣進(jìn)行拉平為16*1,相應(yīng)輸出結(jié)果也會拉平為4*1,圖示如下:
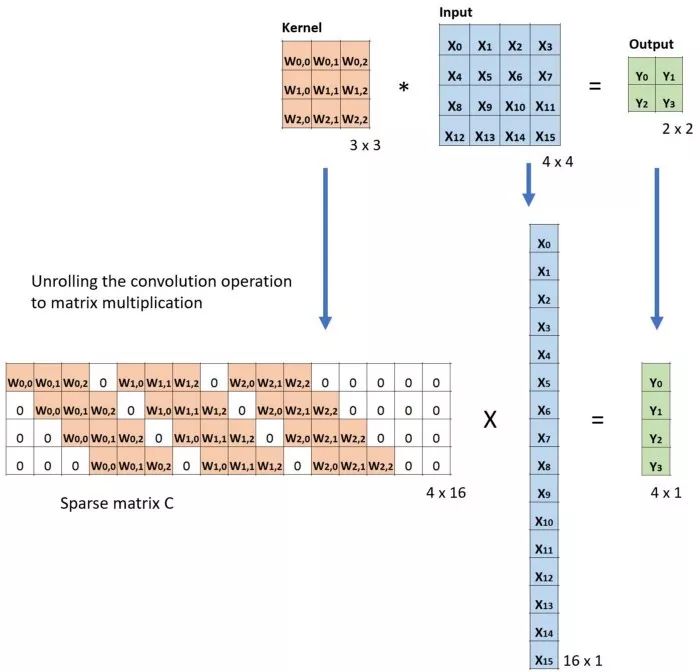
然后按照轉(zhuǎn)置卷積的做法我們把卷積核矩陣進(jìn)行轉(zhuǎn)置,按照X=CTY進(jìn)行驗證:
圖像來自:
https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1
關(guān)于轉(zhuǎn)置卷積的最后一個問題是輸入輸出尺寸計算。我們將常規(guī)卷積的計算公式轉(zhuǎn)化一下即可得到轉(zhuǎn)置卷積的換算公式:
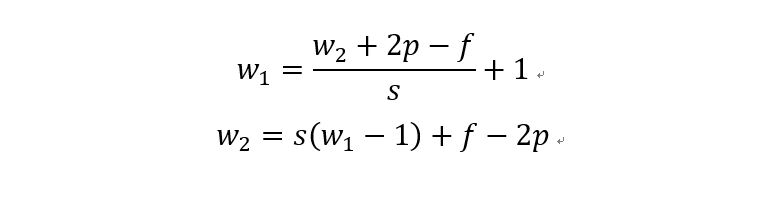
第一個公式就是上面提到的常規(guī)卷積的輸入輸出換算公式,第二個公式為轉(zhuǎn)置卷積的輸入輸出換算公式。其中,s常規(guī)卷積步長,p是常規(guī)卷積的padding,f為濾波器大小。雖說公式推導(dǎo)起來簡單,但考慮到(w2+2p-f)/s極有可能出現(xiàn)不能整除的情況,所以常規(guī)卷積和轉(zhuǎn)置卷積之間的轉(zhuǎn)換關(guān)系就需要分為兩種情況。
第一種就是可以直接整除的。即當(dāng)(w2+2p-f)%s=0時,常規(guī)卷積與轉(zhuǎn)置卷積之間的換算關(guān)系。我們以一組無padding條件下常規(guī)卷積和轉(zhuǎn)置卷積的對比動圖:
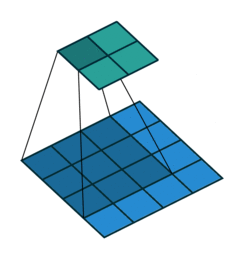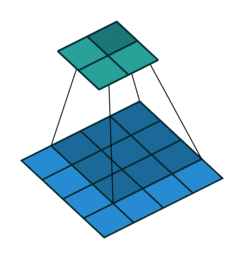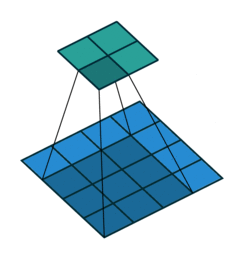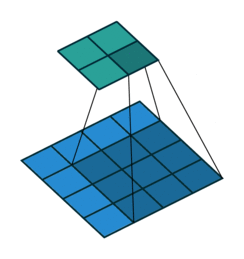
常規(guī)卷積
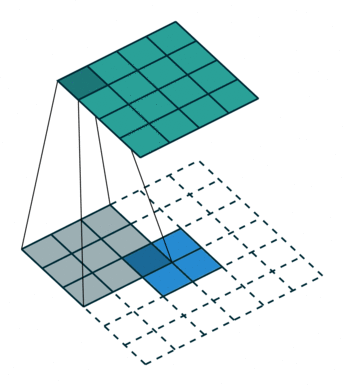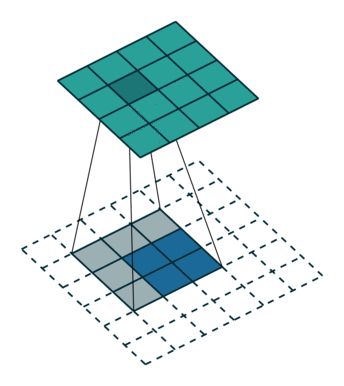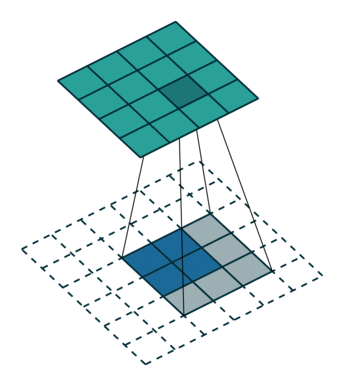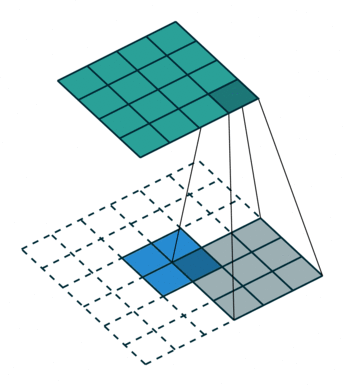
轉(zhuǎn)置卷積
圖像來自:
https://github.com/vdumoulin/conv_arithmetic
在上圖常規(guī)卷積中,輸入為2*2,濾波器為3*3,根據(jù)上述第一個公式可得輸出為(4+2*0-3)/1 + 1=2,這時候是可以整除的,所以輸出為2*2。對應(yīng)到轉(zhuǎn)置卷積中:1*(2-1)+3-2*0=4,即轉(zhuǎn)置卷積的輸出為4*4。
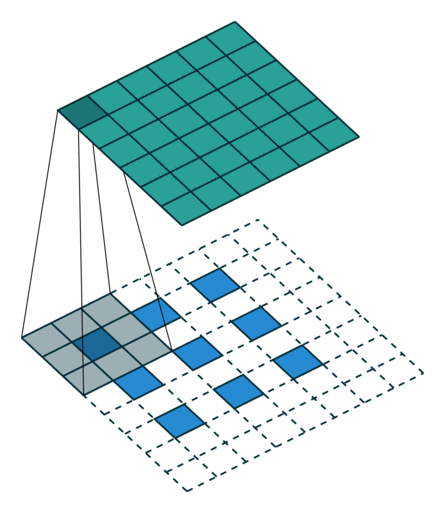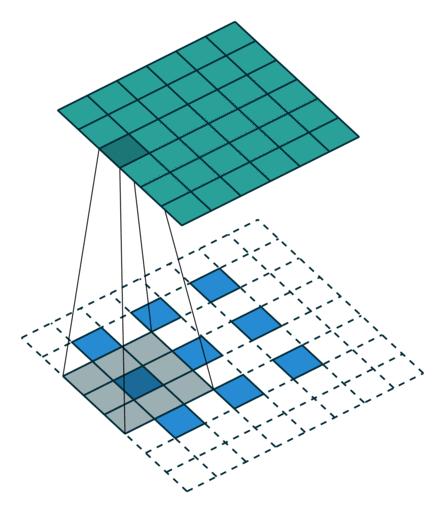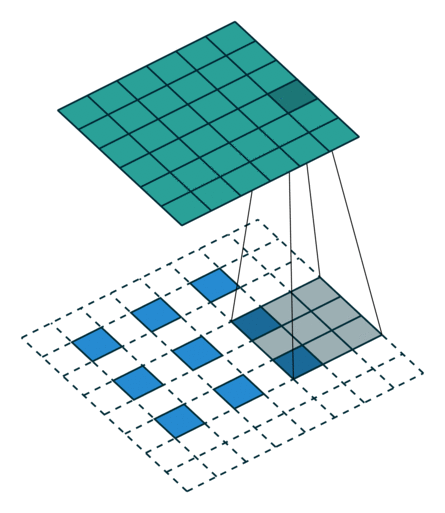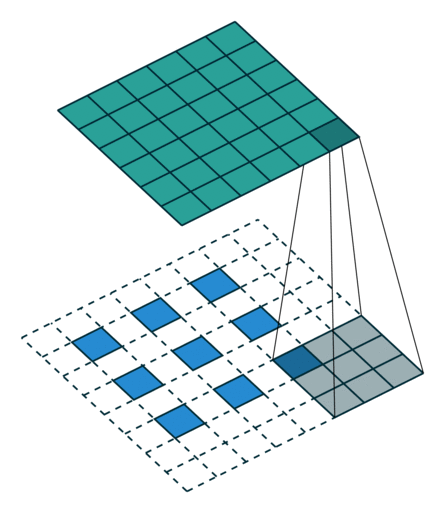
第二種就是略微復(fù)雜一點(diǎn)的不能整除的情況。常規(guī)卷積時不能整除的情況也叫odd卷積。即當(dāng)(w2+2p-f)%s!=0時,常規(guī)卷積與轉(zhuǎn)置卷積之間的換算關(guān)系如何。在進(jìn)行odd卷積時,遇到不能整除的情況下我們通過會進(jìn)行取整操作,因而在常規(guī)卷積時有時候會忽略一小部分像素沒有進(jìn)行卷積,這在轉(zhuǎn)置卷積時需要加回來。我們同樣以一組odd卷積例子來進(jìn)行說明。
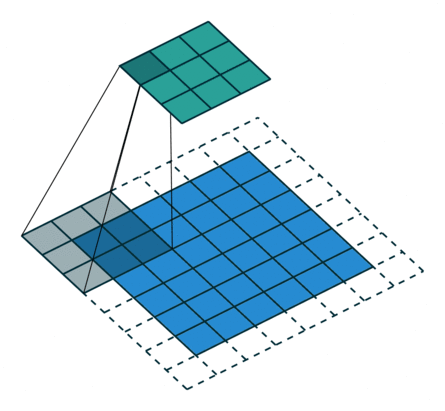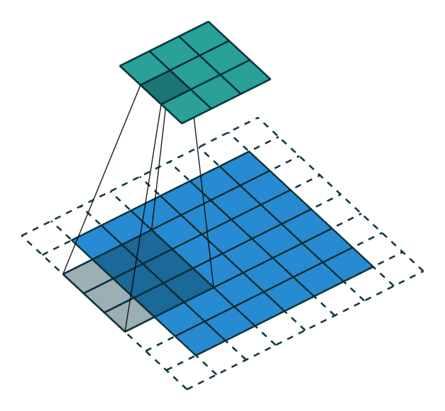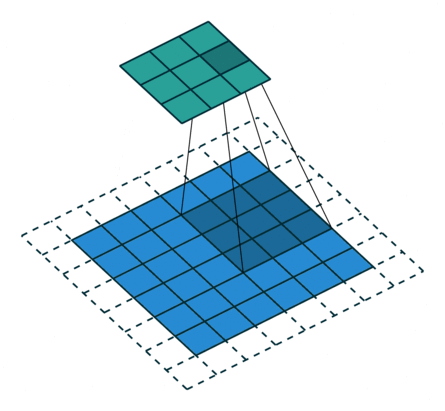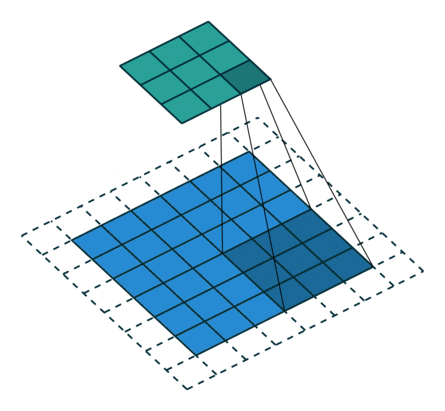
odd常規(guī)卷積
odd轉(zhuǎn)置卷積
圖像來自:
https://github.com/vdumoulin/conv_arithmetic
如上圖所示。在odd常規(guī)卷積中,我們用一個3*3的濾波器對6*6的輸入進(jìn)行卷積,padding=1,stride=2,根據(jù)公式(6+2*1-3)/2,發(fā)現(xiàn)不能整除,這里我們?nèi)≌麨?,那么輸出特征圖大小為3*3。因為做了取整操作,大家可以看到圖中最右邊一列和最下邊一行的padding是沒有加入到卷積計算中的。這部分因取整而舍去的數(shù)據(jù)需要我們在轉(zhuǎn)置卷積時給加回來。所以,對應(yīng)的轉(zhuǎn)置卷積的輸入輸出換算公式可以更改為:
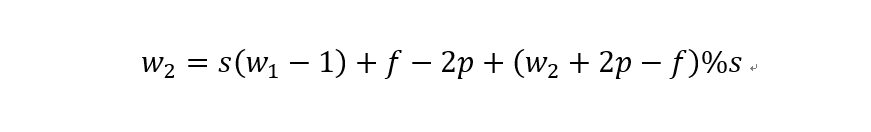
在上圖中,我們輸入尺寸為3*3,卷積濾波器大小也為3*3,padding為1,但這里stride等于2,有同學(xué)可能會問,圖中卷積核明明只移動一個步長啊為啥stride=2?圖中確實只移動了一個步長,但大家可以注意到我們輸入里插入了很多白色塊,也就是0,從當(dāng)前元素值移動到下一個元素值,實際上是經(jīng)過兩個步長的。所以,這里的輸出尺寸為2*(3-1)+3-2*1+1=6。這便是轉(zhuǎn)置卷積。
1x1卷積
1x1卷積的偉大發(fā)明來自于2014年GoogLeNet的inception v1,其主要作用在于可以降維節(jié)省計算成本。1x1卷積在卷積方式上與常規(guī)卷積并無差異,主要在于其應(yīng)用場景和功能。
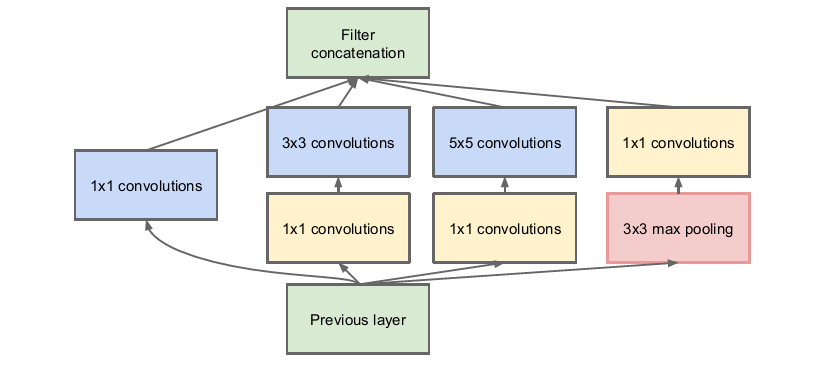
inception v1模塊
下面我們來看1x1卷積到底有什么功效。假設(shè)現(xiàn)在我們有28*28*192的輸入,使用32個5*5*192的卷積核對其進(jìn)行卷積,那么輸出為28*28*32,好像沒什么特別之處。我們來看一下它的計算量,對于輸出中的每一個元素值都要執(zhí)行5*5*192次計算,所以這次卷積的計算量為:28*28*32*5*5*192=120422400。5*5卷積的運(yùn)算量直接上億了。
那現(xiàn)在看看1x1卷積會如何。我們先用16個1*1*192的卷積核對輸入進(jìn)行卷積,輸出尺寸為28*28*16,再用32個5*5*16的卷積核對其進(jìn)行卷積,輸出為28*28*32。經(jīng)歷兩次卷積同樣得到28*28*32的輸出,來看一下其中的計算量。第一次卷積:28*28*16*192=2408448,第二次卷積28*28*32*5*5*16=10035200,兩次卷積合計計算量約為120萬,將較于直接的5*5卷積,1x1卷積的計算量直接減少了10倍,能夠在保證網(wǎng)絡(luò)性能的情況下極大幅度的節(jié)約計算成本。這便是1x1卷積。
深度可分離卷積
從維度的角度看,卷積核可以看成是一個空間維(寬和高)和通道維的組合,而卷積操作則可以視為空間相關(guān)性和通道相關(guān)性的聯(lián)合映射。從inception的1x1卷積來看,卷積中的空間相關(guān)性和通道相關(guān)性是可以解耦的,將它們分開進(jìn)行映射,可能會達(dá)到更好的效果。
深度可分離卷積是在1x1卷積基礎(chǔ)上的一種創(chuàng)新。主要包括兩個部分:深度卷積和1x1卷積。深度卷積的目的在于對輸入的每一個通道都單獨(dú)使用一個卷積核對其進(jìn)行卷積,也就是通道分離后再組合。1x1卷積的目的則在于加強(qiáng)深度。下面以一個例子來看一下深度可分離卷積。
假設(shè)我們用128個3*3*3的濾波器對一個7*7*3的輸入進(jìn)行卷積,可得到5*5*128的輸出。如下圖所示:
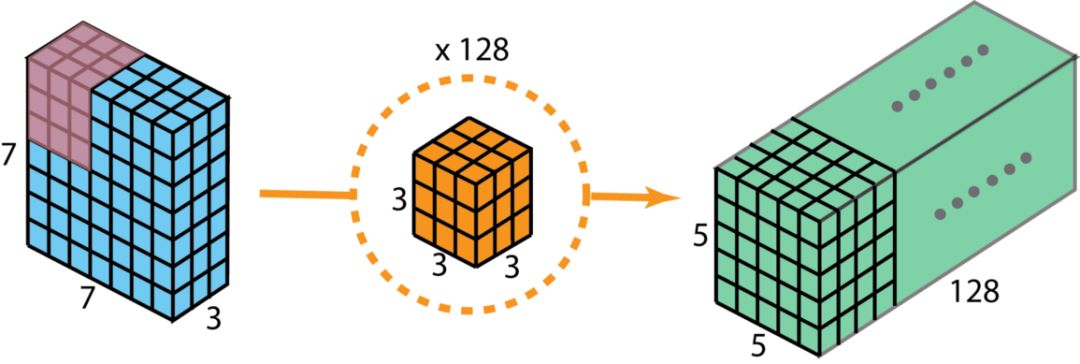
圖像來自:
https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1
其計算量為5*5*128*3*3*3=86400。
現(xiàn)在看如何使用深度可分離卷積來實現(xiàn)同樣的結(jié)果。深度可分離卷積的第一步是深度卷積。這里的深度卷積,就是分別用3個3*3*1的濾波器對輸入的3個通道分別做卷積,也就是說要做3次卷積,每次卷積都有一個5*5*1的輸出,組合在一起便是5*5*3的輸出。
現(xiàn)在為了拓展深度達(dá)到128,我們需要執(zhí)行深度可分離卷積的第二步:1x1卷積。現(xiàn)在我們用128個1*1*3的濾波器對5*5*3進(jìn)行卷積,就可以得到5*5*128的輸出。完整過程如下圖所示:
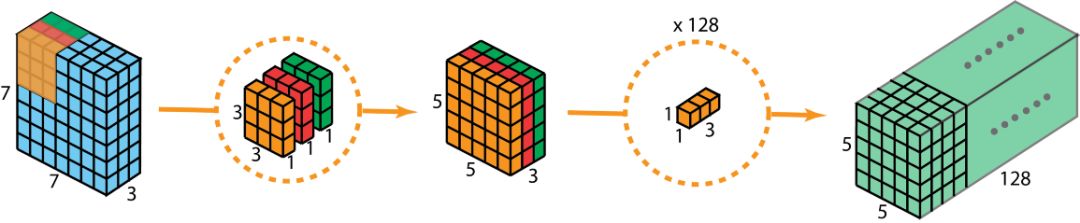
圖像來自:
https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1
那么我們來看一下深度可分離卷積的計算量如何。第一步深度卷積的計算量:5*5*1*3*3*1*3=675。第二步1x1卷積的計算量:5*5*128*1*1*3=9600,合計計算量為10275次。可見,相同的卷積計算輸出,深度可分離卷積要比常規(guī)卷積節(jié)省12倍的計算成本。
典型的應(yīng)用深度可分離卷積的網(wǎng)絡(luò)模型包括xception和mobilenet等。本質(zhì)上而言,xception就是應(yīng)用了深度可分離卷積的inception網(wǎng)絡(luò)。
空洞卷積
空洞卷積也叫擴(kuò)張卷積或者膨脹卷積,簡單來說就是在卷積核元素之間加入一些空格(零)來擴(kuò)大卷積核的過程。我們用一個擴(kuò)展率a來表示卷積核擴(kuò)張的程度。比如說a=1,2,4的時候卷積核核感受野如下圖所示:

圖像來自:
https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1
加入空洞之后的實際卷積核尺寸與原始卷積核尺寸之間的關(guān)系:
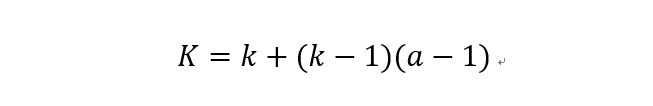
其中k為原始卷積核大小,a為卷積擴(kuò)展率,K為經(jīng)過擴(kuò)展后實際卷積核大小。除此之外,空洞卷積的卷積方式跟常規(guī)卷積一樣。a=2時的空洞卷積的動態(tài)示意圖如下所示:
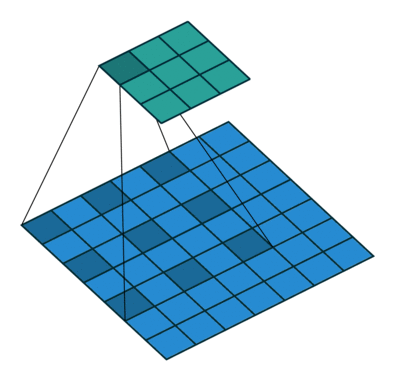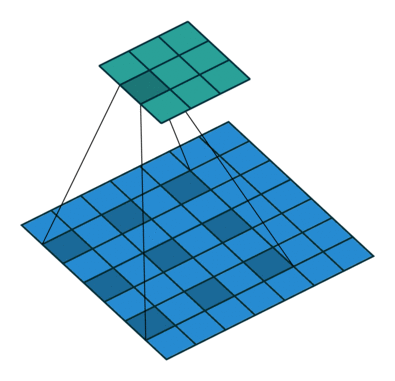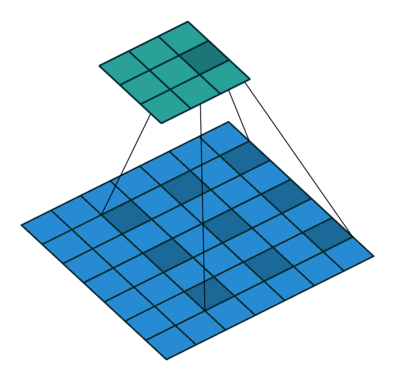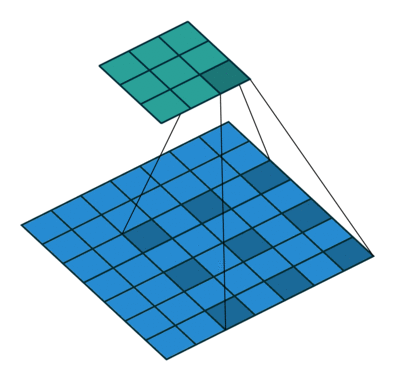
圖像來自:
https://github.com/vdumoulin/conv_arithmetic
那么空洞卷積有什么好處呢?一個直接作用就是可以擴(kuò)大卷積感受野,空洞卷積幾乎可以在零成本的情況下就可以獲取更大的感受野來擴(kuò)充更多信息,這有助于在檢測和分割任務(wù)中提高準(zhǔn)確率。空洞卷積的另一個優(yōu)點(diǎn)則是可以捕捉多尺度的上下文信息,當(dāng)我們使用不同的擴(kuò)展率來進(jìn)行卷積核疊加時,獲取的感受野就豐富多樣。
參考資料:
往期精彩:
【原創(chuàng)首發(fā)】機(jī)器學(xué)習(xí)公式推導(dǎo)與代碼實現(xiàn)30講.pdf
【原創(chuàng)首發(fā)】深度學(xué)習(xí)語義分割理論與實戰(zhàn)指南.pdf
求個在看
