九十一、動(dòng)態(tài)規(guī)劃系列背包問(wèn)題之混合背包
「@Author:Runsen」
背包系列,是動(dòng)態(tài)規(guī)劃里一類典型的問(wèn)題,主要有:01背包,完全背包,多重背包,混合背包,二維費(fèi)用背包,分組背包,有依賴背包和泛化物品等。也就是常說(shuō)的背包九講。
前面說(shuō)了01背包問(wèn)題,完全背包問(wèn)題,多重背包問(wèn)題,其主要是每件物品可選個(gè)數(shù)有區(qū)別。
混合背包是有N種物品和一個(gè)容量為V的背包。有的物品只可以取一次(01背包),有的物品可以取無(wú)限次(完全背包),有的物品可以取的次數(shù)有一個(gè)
混合背包
今天學(xué)習(xí)的混合背包問(wèn)題混合了這三者。
題目是這樣的,來(lái)源:https://www.acwing.com/problem/content/7/
# -1 表示01背包 0表示完全背包 大于0的表示多重背包
輸入樣例
4 5
1 2 -1
2 4 1
3 4 0
4 5 2
輸出樣例:
8
最簡(jiǎn)單的方法就是直接轉(zhuǎn)化為多重背包。-1變成1,0變成V,這樣就是最簡(jiǎn)單最高效的方法。
'''
@Author:Runsen
@WeChat:RunsenLiu
@微信公眾號(hào):Python之王
@CSDN:https://blog.csdn.net/weixin_44510615
@Github:https://github.com/MaoliRUNsen
@Date:2020/9/27
# -1 表示01背包 0表示完全背包 大于0的表示多重背包
輸入樣例
4 5
1 2 -1
2 4 1
3 4 0
4 5 2
輸出樣例:
8
'''
n, v = map(int, input().split())
dp = [0 for _ in range(v+1)]
for i in range(n):
b, w, s = map(int, input().split())
# 這里需要判斷下s
if s == -1 : s = 1
if s == 0 : s = v
for j in range(v, -1, -1):
k = 1
while k <= s and j >= k * b:
dp [j] = max(dp [j], dp [j - k*b] + k*w)
k += 1
print(dp[v])
上次我用了二進(jìn)制的方法進(jìn)行了優(yōu)化,混合背包當(dāng)然也可以轉(zhuǎn)為多重背包的二進(jìn)制的方法。具體代碼如下所示。
'''
@Author:Runsen
@WeChat:RunsenLiu
@微信公眾號(hào):Python之王
@CSDN:https://blog.csdn.net/weixin_44510615
@Github:https://github.com/MaoliRUNsen
@Date:2020/9/27
二進(jìn)制優(yōu)化方法
# -1 表示01背包 0表示完全背包 大于0的表示多重背包
輸入樣例
4 5
1 2 -1
2 4 1
3 4 0
4 5 2
輸出樣例:
8
'''
def binary_divide(volume,price,count):
# 這里需要多count進(jìn)行改正
if count == -1 :count = 1
if count == 0: count = v
divides = []
for i in range(32):
# 從0位開(kāi)始枚舉
cur = 1 << i
# 如果小于枚舉值,說(shuō)明已經(jīng)拆分完畢了
if count < cur:
# 把剩下的部分打包
divides.append((count, count * volume, count * price))
break
else:
# 否則繼續(xù)拆分,打包1 << i個(gè)物品
count -= cur
divides.append((cur, cur * volume, cur * price))
return divides
n,v = map(int, input().split())
goods = []
for i in range(n):
goods.append([int(i) for i in input().split()])
new_good = []
for i in goods:
# 二進(jìn)制拆分 這里需要區(qū)別extend和append的用法
'''
>>> s = []
>>> s.extend([(1, 1, 2), (2, 2, 4), (0, 0, 0)])
>>> s
[(1, 1, 2), (2, 2, 4), (0, 0, 0)]
>>> s[0]
(1, 1, 2)
>>> a = []
>>> a.append([(1, 1, 2), (2, 2, 4), (0, 0, 0)])
>>> a
[[(1, 1, 2), (2, 2, 4), (0, 0, 0)]]
>>> a[0]
[(1, 1, 2), (2, 2, 4), (0, 0, 0)]
'''
new_good.extend(binary_divide(*i))
dp = [0 for _ in range(v+1)]
for item in new_good:
i, j = item[1], item[2]
for k in range(v - i, -1, -1):
dp[k + i] = max(dp[k + i], dp[k] + j)
print(dp[-1])
九月,我等下一個(gè)秋天,也等下一個(gè)你。
二維費(fèi)用的背包問(wèn)題
二維費(fèi)用的背包問(wèn)題。直接讓我想起了Vivo的面試題,具體鏈接
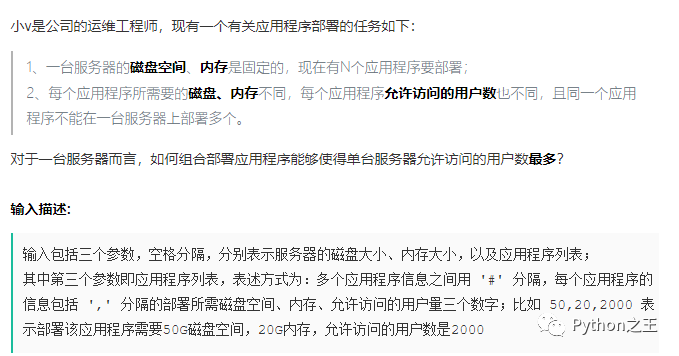
輸入
15 10 5,1,1000#2,3,3000#5,2,15000#10,4,16000
輸出
31000
說(shuō)明
組合部署服務(wù)5,2,15000、10,4,16000 ,可以讓單臺(tái)服務(wù)器承載最大用戶數(shù)31000
那時(shí)候的我不會(huì)做,現(xiàn)在的我實(shí)力有一點(diǎn)滴提高,看看可以A掉不?「這必須A掉」!在vivo這題就是少了一個(gè)服務(wù)器的個(gè)數(shù)。
'''
@Author:Runsen
@WeChat:RunsenLiu
@微信公眾號(hào):Python之王
@CSDN:https://blog.csdn.net/weixin_44510615
@Github:https://github.com/MaoliRUNsen
@Date:2020/9/27
輸入:15 10 5,1,1000#2,3,3000#5,2,15000#10,4,16000
輸出:31000
考點(diǎn):動(dòng)態(tài)規(guī)劃
'''
'''
Welcome to vivo !
'''
def solution(total_disk, total_memory, app_list):
# 背包的二維費(fèi)用問(wèn)題 三維dp解決
disk_sum = []
memory_sum = []
apps = []
for i in app_list:
disk_sum.append(i[0])
memory_sum.append(i[1])
apps.append(i[2])
n = len(apps)
# 狀態(tài) 三維dp dp[i][j][k] 表示第i個(gè)服務(wù)器,磁盤空間為j,內(nèi)存為k的最大APP部署應(yīng)用的個(gè)數(shù)
# dp[i][j][k] 要么就是第i-1個(gè)服務(wù)器,磁盤空間為j,內(nèi)存為k的最大APP部署應(yīng)用的個(gè)數(shù),
# 要么就是第i-1個(gè)服務(wù)器,磁盤空間為j-(i-1)的空間,內(nèi)存為k-(i-1)的空間的最大APP部署應(yīng)用的個(gè)數(shù)(需要判斷當(dāng)前j和k能不能大于i-1的狀態(tài)
# 這里需要注意:為什么dp定義成n+1?
dp = [[[0] * (total_memory + 1) for _ in range(total_disk + 1)] for _ in range(n + 1)]
# 因?yàn)樽詈蟮囊粋€(gè)n+1,需要取到n
for i in range(1, n + 1):
for j in range(1, 1 + total_disk):
for k in range(1, 1 + total_memory):
# 需要判斷當(dāng)前j和k能不能大于i-1的狀態(tài)
if j - disk_sum[i - 1] >= 0 and k - memory_sum[i - 1] >= 0:
dp[i][j][k] = max(dp[i - 1][j][k], dp[i - 1][j - disk_sum[i - 1]][k - memory_sum[i - 1]] + apps[i - 1])
else:
# 判罰失敗,只有一種來(lái)源
dp[i][j][k] = dp[i-1][j][k]
return dp[-1][-1][-1]
if __name__ == "__main__":
# 15 10 5,1,1000#2,3,3000#5,2,15000#10,4,16000
input1 = input()
disk = int(input1.split()[0])
memory = int(input1.split()[1])
input2 = input1.split()[2]
app_list = [[int(j) for j in i.split(',')] for i in input2.split('#')]
print(solution(disk, memory, app_list))
# 順便更新將三維空間壓縮成二維空間的超級(jí)簡(jiǎn)單的做法
input1 = input()
A = int(input1.split()[0])
B = int(input1.split()[1])
input2 = input1.split()[2]
app_list = [[int(j) for j in i.split(',')] for i in input2.split('#')]
dp = [[0 for _ in range(B+1)] for _ in range(A+1)]
for a,b,c in app_list:
for j in range(A, a - 1, -1):
for k in range(B, b - 1, -1):
dp[j][k] = max(dp[j][k], dp[j - a][k - b] + c)
print(dp[-1][-1])
15 10 5,1,1000#2,3,3000#5,2,15000#10,4,16000
31000
我重新來(lái)看二維費(fèi)用的背包問(wèn)題
只要知道了三維的dp的狀態(tài)轉(zhuǎn)移方程:dp[i][j][k] = max(dp[i-1][j][k],dp[i-1][j-V[i-1]][k-M[i-1]]+W[i-1])。
'''
@Author:Runsen
@WeChat:RunsenLiu
@微信公眾號(hào):Python之王
@CSDN:https://blog.csdn.net/weixin_44510615
@Github:https://github.com/MaoliRUNsen
@Date:2020/9/27
'''
n,v,m = map(int,input().split())
dp = [[[0] * (m+1) for _ in range(v+1)] for _ in range(n+1)]
V = []
M = []
W = []
for i in range(n):
# 體積、重量和價(jià)值
a,b,c = map(int,input().split())
V.append(a)
M.append(b)
W.append(c)
for i in range(1,n+1):
# j是容量
for j in range(1,v+1):
# k是重量
for k in range(1,m+1):
if j-V[i-1] >= 0 and k-M[i-1] >= 0:
dp[i][j][k] = max(dp[i-1][j][k],dp[i-1][j-V[i-1]][k-M[i-1]]+W[i-1])
else:
dp[i][j][k] = dp[i-1][j][k]
print(dp[-1][-1][-1])
下面教大家一個(gè)通神的方法,叫做逆序,可以將三維dp直接進(jìn)行空間優(yōu)化成二維dp,其原理就是斐波那契數(shù)列的從底向頂?shù)淖龇ǎ嫦蛩季S。
'''
@Author:Runsen
@WeChat:RunsenLiu
@微信公眾號(hào):Python之王
@CSDN:https://blog.csdn.net/weixin_44510615
@Github:https://github.com/MaoliRUNsen
@Date:2020/9/27
'''
n,v,m = map(int,input().split())
dp = [[0 for _ in range(m+1)] for _ in range(v+1)]
for i in range(n):
# 體積、重量和價(jià)值
a, b, c = map(int, input().split())
for j in range(v, a - 1, -1):
for k in range(m, b - 1, -1):
dp[j][k] = max(dp[j][k], dp[j - a][k - b] + c)
print(dp[-1][-1])
背包系列還有,分組背包,有依賴背包和泛化物品(方案數(shù)),在此個(gè)人覺(jué)得沒(méi)有必要了,掌握零一背包、多重背包、完全背包和混合背包已經(jīng)很不錯(cuò)了。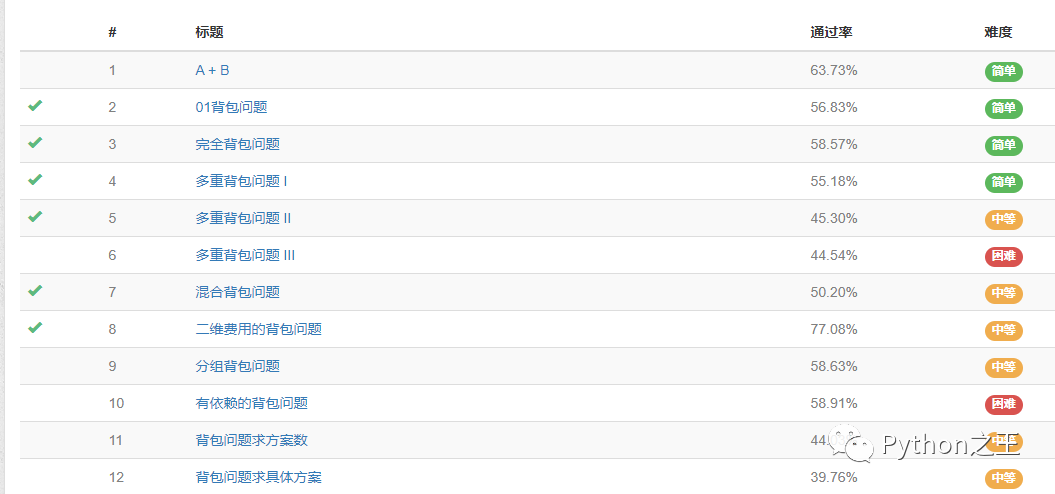
更多的文章
點(diǎn)擊下面小程序
- END -

