九十四、動態(tài)規(guī)劃系列之路徑問題
「@Author:Runsen」
在動態(tài)規(guī)劃最短路徑經(jīng)常提及,在上幾篇介紹過相關(guān)的最短路徑的問題,介紹過使用Dijkstra算法去求解,但是Dijkstra算法是基于貪心算法,按路徑長度遞增的次序一步一步并入來求取,算法效率低效。
Dijkstra算法原理是:如果從圖中某一頂點(源點)到達另一頂點(終點)的路徑可能不止一條,如何找到一條路徑使得沿此路徑上各邊的權(quán)值總和(稱為路徑長度)達到最小。動態(tài)規(guī)劃可以說算法中最優(yōu)秀的算法,因為在此介紹動態(tài)規(guī)劃系列中的路徑問題。
下面是對應(yīng)的動態(tài)規(guī)劃解決的路徑問題總結(jié):
62. 不同路徑 63. 不同路徑 II 64. 最小路徑和 120. 三角形最小路徑和
62.不同路徑
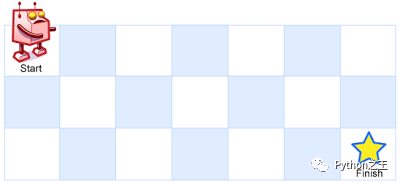
一個機器人位于一個 m x n 網(wǎng)格的左上角 (起始點在下圖中標記為 “Start” )。
機器人每次只能向下或者向右移動一步。機器人試圖達到網(wǎng)格的右下角(在下圖中標記為 “Finish” )。
問總共有多少條不同的路徑?
下面是測試用例:
輸入:m = 3, n = 7
輸出:28
在此,我們可以完全當作一道初中數(shù)學(xué)題來對待,既然最后要到達終點,那肯定需要往下走n-1步,往右走m-1步,總共需要走n+m-2步。
還有無論往右走還是往下走他的總的步數(shù)是不會變的,往右走的步數(shù)一定等于n,往下走的步數(shù)一定等于m。
因此,可以換一種說法相當于總共要走n+m-2步,往右走m-1步,總共有多少種走法,很明顯這就是一個高中數(shù)學(xué)的排列組合問題,公式如下
排列組合的計算公式:
代入就可以得到:
# factorial求階乘,也可以自己定義一個
import math
def uniquePaths(self, m: int, n: int) -> int:
return int(math.factorial(m+n-2)/math.factorial(m-1)/math.factorial(n-1))
上面的方法沒有開數(shù)組空間,無論是時間還是空間,都是最優(yōu)的做法。
對于動態(tài)規(guī)劃的方法,也非常容易理解,定義一個二維數(shù)組dp,來存儲每一個格子的最短路徑數(shù)之和,設(shè) dp 為大小 矩陣,其中 dp[i][j] 的值代表直到走到 (i,j) 的最小路徑和。
由于只能向右向下移動,所以對于除了邊界外的格子之外的其他格子而言,到達它的方式只能有它上邊的格子下移或者左邊的格子右移,所以到達它的路徑數(shù)為它上邊格子的路徑數(shù)與左邊格子的路徑數(shù)之和,可得狀態(tài)轉(zhuǎn)移方程:dp[i][j] = dp[i-1][j] + dp[i][j-1]。
下圖是二維數(shù)組動態(tài)規(guī)劃求解的過程:
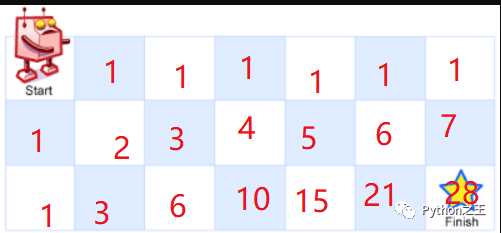
dp初始化,對于第一行 dp[0][j],或者第一列 dp[i][0],由于都是在邊界,所以只能為 1。
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [[0] * n for _ in range(m)]
# 初始化
for i in range(m):
dp[i][0] = 1
for j in range(n):
dp[0][j] = 1
# 根據(jù)轉(zhuǎn)移方程進行遞推
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[-1][-1]
當然,你也可以對二維dp數(shù)組壓縮成一維數(shù)組,來代表每一行或者每一列的路徑數(shù)之和,可以對空間進一步的優(yōu)化。
63. 不同路徑 II
此題和第一題的添加了一個障礙物,那么從左上角到右下角將會有多少條不同的路徑?
網(wǎng)格中的障礙物和空位置分別用 1 和 0 來表示。
測試用例:
輸入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
輸出:2
解釋:
3x3 網(wǎng)格的正中間有一個障礙物。
從左上角到右下角一共有 2 條不同的路徑:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
假設(shè)自己畫的方框是障礙物,那么直接把二維數(shù)組對應(yīng)的位置變成0即可。
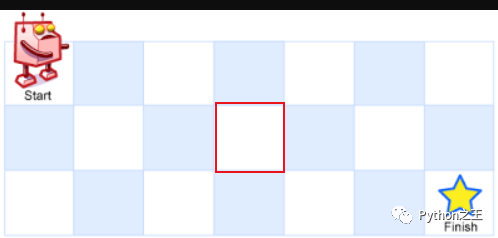
因此,最終的解決過程:
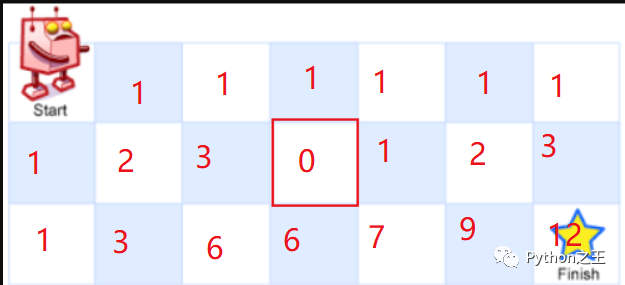
在此題中,測試用例存在門口就是一個障礙物的情況,因此需要注意初始化條件。
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m, n = len(obstacleGrid), len(obstacleGrid[0])
# 門口是一個障礙物
if obstacleGrid[0][0] == 1:
return 0
dp = [[0 for _ in range(n)] for _ in range(m)]
dp[0][0] = 1
for i in range(1, m):
if obstacleGrid[i][0] == 0:
dp[i][0] = dp[i-1][0]
for j in range(1, n):
if obstacleGrid[0][j] == 0:
dp[0][j] = dp[0][j-1]
for i in range(1, m):
for j in range(1, n):
# 判斷是不是障礙物
if obstacleGrid[i][j] == 1:
dp[i][j] = 0
else:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[-1][-1]
64. 最小路徑和
給定一個包含非負整數(shù)的 m x n 網(wǎng)格,請找出一條從左上角到右下角的路徑,使得路徑上的數(shù)字總和為最小。
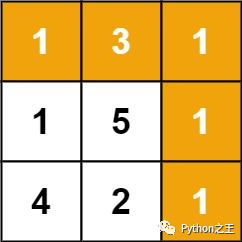
測試用例:
輸入:grid = [[1,3,1],[1,5,1],[4,2,1]]
輸出:7
解釋:因為路徑 1→3→1→1→1 的總和最小。
如果采用貪心的算法,會由于顧及當前的利益,而放棄長遠的利益。因此貪心的思路直接否決。
在此題的動態(tài)規(guī)劃中,狀態(tài)轉(zhuǎn)移方程仍是:dp[i][j] = dp[i-1][j] + dp[i][j-1]。
初始化dp所有的元素均為0,在網(wǎng)格的第一行和第一列的所有路徑和應(yīng)該都是固定的,因為都是向右或者向下移動。
而當位置(i,j)處時,需要從判斷從向右和向下的dp的數(shù)值,取出最小值,然后加上這個網(wǎng)格的數(shù)字。
dp[i][j] = min(dp[i-1][j] +grid[i][j],dp[i][j-1]++grid[i][j])
from typing import List
class Solution:
def minPathSum(self, grid: [[int]]) -> int:
for i in range(len(grid)):
for j in range(len(grid[0])):
if i == j == 0: continue
elif i == 0:
grid[i][j] = grid[i][j - 1] + grid[i][j]
elif j == 0:
grid[i][j] = grid[i - 1][j] + grid[i][j]
else: grid[i][j] = min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j]
return grid[-1][-1]
if __name__ == "__main__":
s=Solution()
t=[[1,3,1],
[1,5,1],
[4,2,1]]
print(s.minPathSum(t))
# result
7
120. 三角形最小路徑和
此題三角形最小路徑和變換了輸入的矩陣,給定一個三角形 triangle ,找出自頂向下的最小路徑和。
測試用例
輸入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
輸出:11
解釋:如下面簡圖所示:
2
3 4
6 5 7
4 1 8 3
2
3 4
6 5 7
4 1 8 3
自頂向下的最小路徑和為 11(即,2 + 3 + 5 + 1 = 11)。
此題由于空間在壓縮,因此使用一維動態(tài)歸化數(shù)組,定義dp[i]為到第N層第i個節(jié)。
要想獲得到達第 m 條邊的最小路徑和,需要先獲得到達第m - 1 條邊的最小路徑和。
由于動態(tài)規(guī)劃可以采用自底向上的逆推思想,也就是把三角形倒過來看。

狀態(tài)轉(zhuǎn)移方程:dp[j] = min(dp[j], dp[j + 1]) + triangle[i][j]
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
dp = triangle[-1]
for i in range(len(triangle)-2,-1,-1):
for j in range(i+1):
dp[j] = triangle[i][j] + min(dp[j],dp[j+1])
return dp[0]
對于原地自頂向下算法,把到達每一層的每個數(shù)的最小路徑都算出來,判斷三種不同狀態(tài)的,根據(jù)下面的狀態(tài)轉(zhuǎn)移方程,不斷地修改原數(shù)組 。

自頂向下算法可以直接用triangle本身的變量進行計算,達到減小內(nèi)存開銷的效果。
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
if len(triangle)==0:
return 0
#動態(tài)規(guī)劃 dp表示走到當前位置的時候的最小路徑
for i in range(1,len(triangle)):
for j in range(len(triangle[i])):
if j==0: #最左邊的情況
triangle[i][j]+=triangle[i-1][j]
elif j==i: #最右邊的情況
triangle[i][j]+=triangle[i-1][j-1]
else:
triangle[i][j]+=min(triangle[i-1][j-1],triangle[i-1][j])
return min(triangle[-1]) #返回最后一層最小的一個
更多的文章
點擊下面小程序
- END -

