【統(tǒng)計學(xué)習(xí)方法】 第4章 樸素貝葉斯法(二)
點擊上方“公眾號”可訂閱哦!
這篇文章主要介紹使用sklearn開源庫,實現(xiàn)三種樸素貝葉斯算法。
常用的三種樸素貝葉斯為:
高斯樸素貝葉斯
伯努利樸素貝葉斯
多項式樸素貝葉斯
1
●
高斯樸素貝葉斯
適用于連續(xù)變量,其假定各個特征xi在各個類別y下是服從正態(tài)分布的,算法內(nèi)部使用正態(tài)分布的概率密度函數(shù)來計算概率如下:
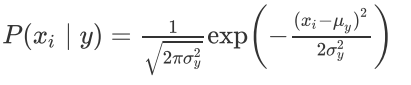

代碼演示:
import numpy as npimport pandas as pdfrom sklearn.naive_bayes import GaussianNBnp.random.seed(0)# 當(dāng)我們預(yù)先使用 random.seed(x) 設(shè)定好種子之后,# 其中的 x 可以是任意數(shù)字,如10,這個時候,先調(diào)用它的情況下,# 使用 random() 生成的隨機數(shù)將會是同一個x = np.random.randint(0,10,size=(6,2))y = np.array([0,0,0,1,1,1])data = pd.DataFrame(np.concatenate([x, y.reshape(-1,1)], axis=1), columns=['x1','x2','y'])# pd.DataFrame,主要包含三個參數(shù),data=數(shù)據(jù), index=行名稱, columns=列名稱# y.reshape(-1,1) 把y變成只有一列,行數(shù)Numpy自動計算出來display(data)gnb = GaussianNB()gnb.fit(x,y)#每個類別的先驗概率print('概率:', gnb.class_prior_)#每個類別樣本的數(shù)量print('樣本數(shù)量:', gnb.class_count_)#每個類別的標簽print('標簽:', gnb.classes_)#每個特征在每個類別下的均值print('均值:',gnb.theta_)#每個特征在每個類別下的方差print('方差:',gnb.sigma_)#測試集x_test = np.array([[6,3]])print('預(yù)測結(jié)果:', gnb.predict(x_test))print('預(yù)測結(jié)果概率:', gnb.predict_proba(x_test))
輸出:
| x1 | x2 | y | |
|---|---|---|---|
| 0 | 5 | 0 | 0 |
| 1 | 3 | 3 | 0 |
| 2 | 7 | 9 | 0 |
| 3 | 3 | 5 | 1 |
| 4 | 2 | 4 | 1 |
| 5 | 7 | 6 | 1 |
概率:[0.5 0.5]
樣本數(shù)量:[3. 3.]
標簽:[0 1]
均值:[[5. 4.]
[4. 5.]]
方差:[[ 2.66666667 14.00000001]
[ 4.66666667 0.66666667]]
預(yù)測結(jié)果:[0]
預(yù)測結(jié)果概率:[[0.87684687 0.12315313]]2
●
伯努利樸素貝葉斯
設(shè)試驗E只有兩個可能的結(jié)果:A與Aˉ,則稱為E為伯努利試驗。
伯努利樸素貝葉斯,適用于離散變量,其假設(shè)各個特征xi在各個類別y下是服從n重伯努利分布(二項分布)的,因為伯努利試驗僅有兩個結(jié)果,因此,算法會首先對特征值進行二值化處理(假設(shè)二值化的結(jié)果為1與0)。
計算方式如下:
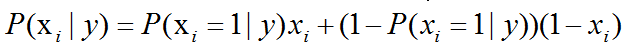
在訓(xùn)練集中,會進行如下的估計:
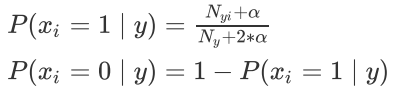

代碼演示:
from sklearn.naive_bayes import BernoulliNBnp.random.seed(0)x = np.random.randint(-5,5,size=(6,2))y = np.array([0,0,0,1,1,1])data = pd.DataFrame(np.concatenate([x,y.reshape(-1,1)], axis=1), columns=['x1','x2','y'])display(data)bnb = BernoulliNB()bnb.fit(x,y)#每個特征在每個類別下發(fā)生(出現(xiàn))的次數(shù)。因為伯努利分布只有兩個值。#我們只需要計算出現(xiàn)的概率P(x=1|y),不出現(xiàn)的概率P(x=0|y)使用1減去P(x=1|y)即可。print('數(shù)值1出現(xiàn)次數(shù):', bnb.feature_count_)#每個類別樣本所占的比重,即P(y)。注意該值為概率取對數(shù)之后的結(jié)果,#如果需要查看原有的概率,需要使用指數(shù)還原。print('類別占比p(y):',np.exp(bnb.class_log_prior_))#每個類別下,每個特征(值為1)所占的比例(概率),即p(x|y)#該值為概率取對數(shù)之后的結(jié)果,如果需要查看原有的概率,需要使用指數(shù)還原print('特征概率:',np.exp(bnb.feature_log_prob_))
輸出:
| x1 | x2 | y | |
|---|---|---|---|
| 0 | 0 | -5 | 0 |
| 1 | -2 | -2 | 0 |
| 2 | 2 | 4 | 0 |
| 3 | -2 | 0 | 1 |
| 4 | -3 | -1 | 1 |
| 5 | 2 | 1 | 1 |
數(shù)值1出現(xiàn)次數(shù):[[1. 1.]
[1. 1.]]
類別占比p(y):[0.5 0.5]
特征概率:[[0.4 0.4]
[0.4 0.4]]3
●
多項式樸素貝葉斯
多項式樸素貝葉斯,適用于離散變量,其假設(shè)各個特征xi在各個類別y下是服從多項式分布的,故每個特征值不能是負數(shù)。
計算如下:

代碼演示:
from sklearn.naive_bayes import MultinomialNBnp.random.seed(0)x = np.random.randint(0,4,size=(6,2))y = np.array([0,0,0,1,1,1])data = pd.DataFrame(np.concatenate([x,y.reshape(-1,1)], axis=1), columns=['x1','x2','y'])display(data)mnb = MultinomialNB()mnb.fit(x,y)#每個類別的樣本數(shù)量print(mnb.class_count_)#每個特征在每個類別下發(fā)生(出現(xiàn))的次數(shù)print(mnb.feature_count_)#每個類別下,每個特征所占的比例(概率),即P(x|y)#該值為概率取對數(shù)之后的結(jié)果,如果需要查看原有的概率,需要使用指數(shù)還原print(np.exp(mnb.feature_log_prob_))
輸出:
| x1 | x2 | y | |
|---|---|---|---|
| 0 | 0 | 3 | 0 |
| 1 | 1 | 0 | 0 |
| 2 | 3 | 3 | 0 |
| 3 | 3 | 3 | 1 |
| 4 | 1 | 3 | 1 |
| 5 | 1 | 2 | 1 |
[3. 3.]
[[4. 6.]
[5. 8.]]
[[0.41666667 0.58333333]
[0.4 0.6 ]]
參考來源:
https://blog.csdn.net/ws19920726/article/details/105726570
END

深度學(xué)習(xí)入門筆記
微信號:sdxx_rmbj
日常更新學(xué)習(xí)筆記、論文簡述
評論
圖片
表情
