面試管：如何找出字符串中無重復最長子串？

前言

LeetCode第3題，“無重復字符的最長子串”，曾經(jīng)面試的過程中遇到過的一道算法題。通過這道題，我們能夠學到算法中一個比較常見的解題方法：滑動窗口算法。

由于LeetCode中很多題都是基于“滑動窗口算法”進行解答，因此本篇文章將重點放在“滑動窗口”上，而不僅僅是這道算法題。當理解了滑動窗口的基本原理之后，所有類似的題都可以輕易解答。

下面來看具體的題目和解題方法。

“無重復字符的最長子串”

題目鏈接：https://leetcode-cn.com/problems/longest-substring-without-repeating-characters/

題目描述：

給定一個字符串，請你找出其中不含有重復字符的 最長子串 的長度。

示例：

輸入:?s?=?"abcabcbb"
輸出:?3?
解釋:?因為無重復字符的最長子串是?"abc"，所以其長度為 3。

題目說明

題目很簡單，就是從一個字符串中找出不包含重復字符的最長子串的長度。

該題如果用暴利破解的方法進行循環(huán)判斷，則時間復雜度直接變?yōu)镺(n^2)，是比較恐怖的。因此，可采取滑動窗口的方法來降低時間復雜度。

什么是滑動窗口？

滑動窗口算法是在一個特定大小的字符串或數(shù)組上進行操作，而不在整個字符串和數(shù)組上操作，這就降低了問題的復雜度，從而也降低了循環(huán)的嵌套深度。滑動窗口主要應用在數(shù)組和字符串的場景。

簡單示例

先通過一個簡單的示例來看一下滑動窗口的運作，比如有一個數(shù)組[1,3,5,6,2,2]，設定滑動窗口（window）大小為3，那么當窗口從數(shù)組開始位置滑動到最終位置時依次計算每個窗口內3個元素的和，表示為sum。

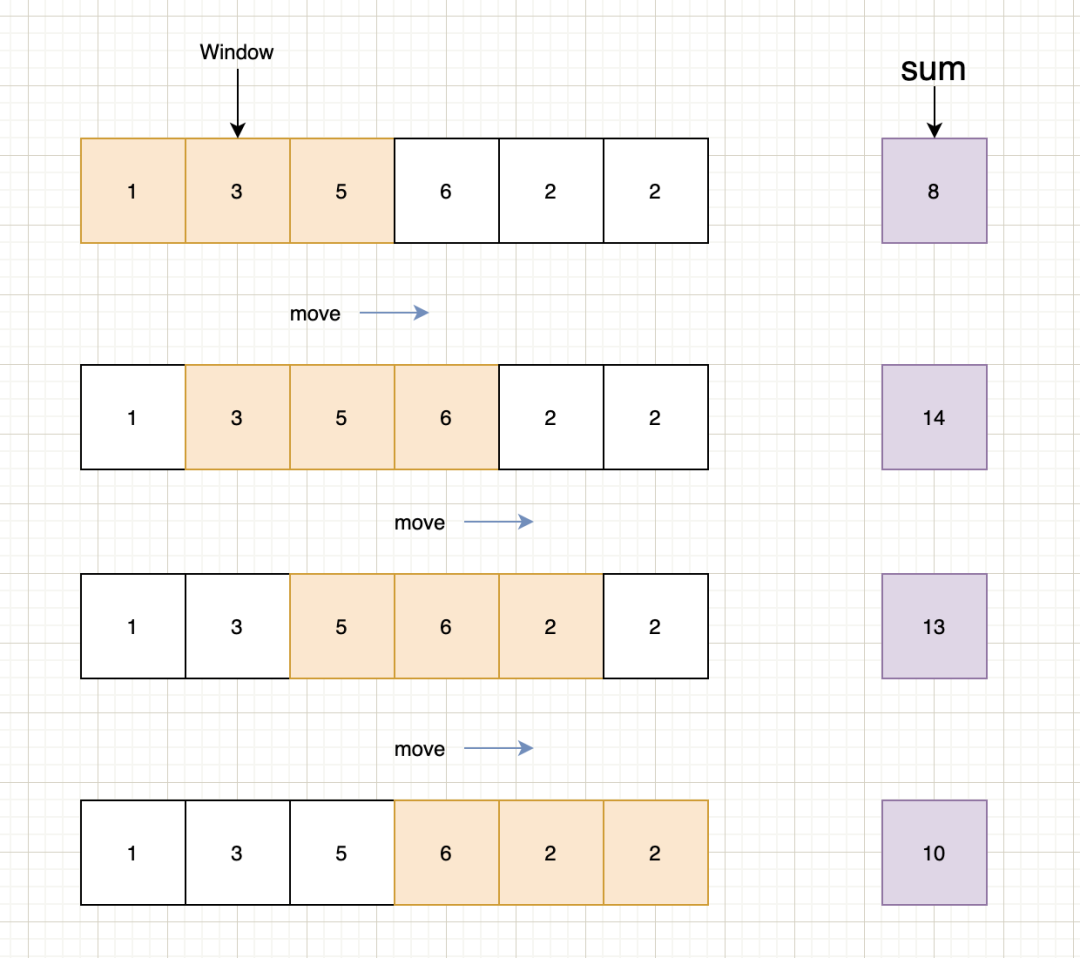
上圖我們可以看出，隨著窗口在數(shù)組上向右移動，窗口內的數(shù)據(jù)也在不斷變化，我們只用對窗口內連續(xù)區(qū)間內的數(shù)據(jù)進行處理即可。由于區(qū)間是連續(xù)的，因此當窗口移動時只用對舊窗口的數(shù)據(jù)進行裁剪處理，這樣便減少了重復計算，降低了時間復雜度。

以上圖為例，當窗口位于[1,3,5]時，處理完該窗口的數(shù)據(jù)之后，將窗口向右移動一格，等于是將原有窗口左邊的1裁剪掉，然后將窗口右邊的6添加上，而整個過程看起來就像窗口在向右移動一樣。

對于類似“請找到滿足 xx 的最 x 的區(qū)間（子串、子數(shù)組）的 xx ”這類問題都可以使用該方法進行解決。

滑動窗口的基本步驟

需要注意的是：窗口的移動是按照移動的順序來進行的；窗口的大小不一定是固定的，可以不斷縮小或變大的。

對于滑動窗口算法的基本解題思路，以字符串S示例如下：

• （1）采用雙指針來指定窗口的范圍，初始化left=right=0，而索引閉區(qū)間[left,right]便是一個窗口。
• （2）不斷增大窗口的right指針，直到窗口中的字符串滿足條件。
• （3）此時，停止right的增加，轉而不斷增加left指針，用于縮小窗口[left,right]，直到窗口中的字符串不再符合要求。每增加一次left，需要更新一輪結果。
• （4）重復第2和第3步，直到right到達字符串的盡頭。

其中，第2步相當于在尋找一個「可行解」，然后第3步在優(yōu)化這個「可行解」，最終找到最優(yōu)解。左右指針輪流前進，窗口大小增增減減，窗口不斷向右滑動。

解題

學習了窗口滑動之后，我們回到LeetCode的題目上，是將上述示例的固定窗口變?yōu)榱俗兓笮〉拇翱冢鴮⑶蠛蛽Q成了判斷是否包含指定字符。

因此，套用上面的思路來進行分析。以字符串“dvdf”為例，通過下圖來演示滑動的過程。

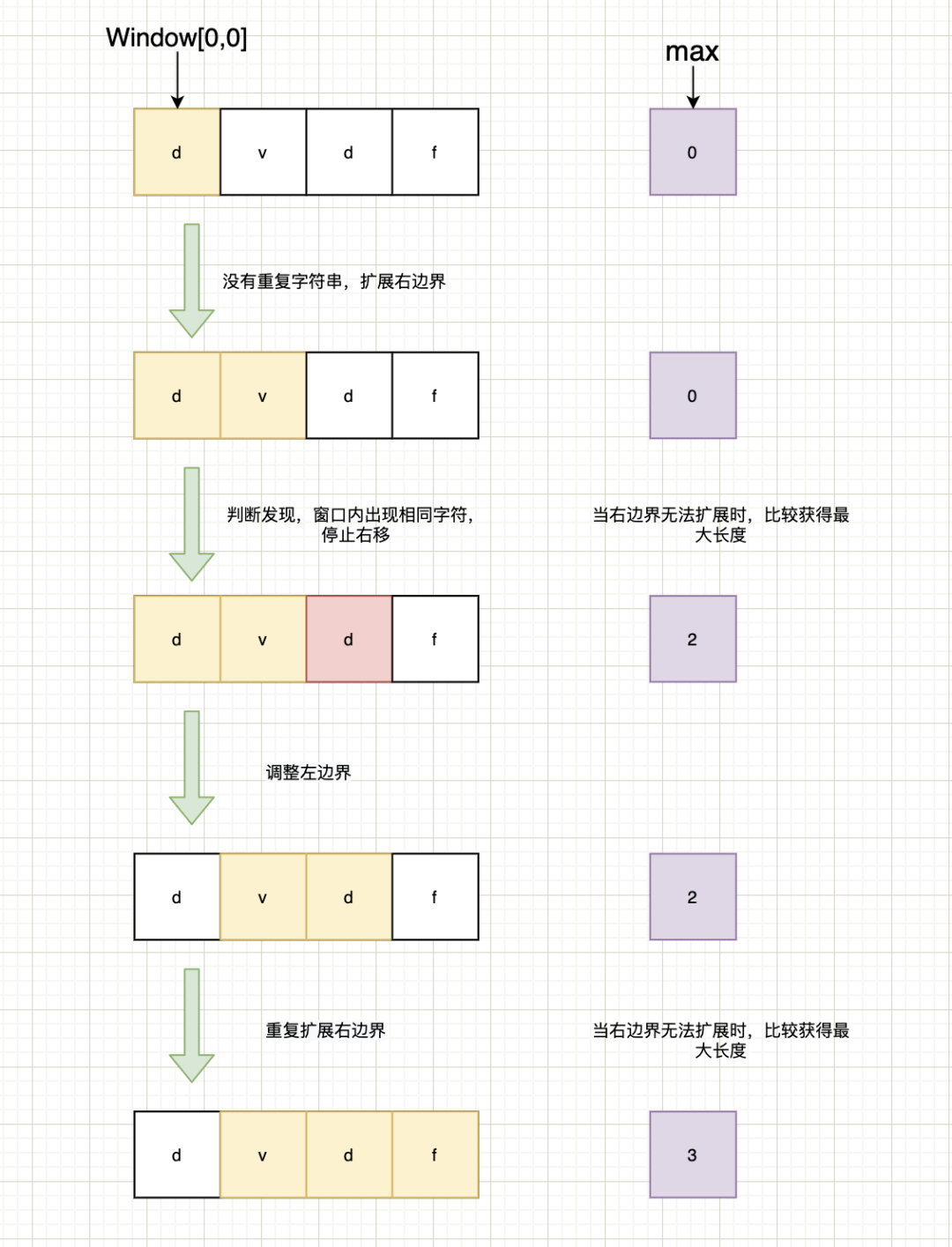
在上述流程中，可分解為以下步驟：

• （1）選定初始值left=right=0，也就是窗口[0,0]。
• （2）判斷right右邊字符在窗口內是否已經(jīng)存在；
• （3）發(fā)現(xiàn)字符v在窗口中沒有，則可right右移一位，窗口變?yōu)閇0,1]；
• （4）繼續(xù)擴展右邊界，right=2，發(fā)現(xiàn)d已經(jīng)存在于窗口當中，則停止繼續(xù)右移；
• （5）此時窗口的長度便是以d開通的子串的長度，比較當前窗口長度和歷史max（默認值0）大小，發(fā)現(xiàn)2>0，于是更新max為2。
• （6）開始移動left，窗口變?yōu)閇1,1]；
• （7）繼續(xù)擴展右邊界，發(fā)現(xiàn)d不存在于窗口當中，此時窗口變?yōu)閇1,2]；
• （8）繼續(xù)擴展右邊界，發(fā)現(xiàn)f不存在于窗口當中，此時窗口變?yōu)閇1,3]；
• （9）到達字符串的最大長度，停止右移，此時比較當前窗口長度和歷史max大小，發(fā)現(xiàn)3>2，于是更新max為3。
• （10）得出，不包含重復字符的最長子串的長度3。

理解了上述步驟，我們再來看原題的Java代碼實現(xiàn)：

class?Solution?{
????public?int?lengthOfLongestSubstring(String?s)?{
????????int?n?=?s.length();
????????int?k?=?0,?max?=?0;
????????Set?set?=?new?HashSet<>();
????????for(int?i=0;?i????????????if(i?!=?0){
????????????????set.remove(s.charAt(i-1));
????????????}

????????????while(k?????????????????set.add(s.charAt(k));
????????????????k++;
????????????}
????????????max?=?Math.max(max,set.size());
????????}
????????return?max;
????}
}

上述代碼中for循環(huán)中的i相當于left，k相當于right，而max是存儲歷史最長字符串的值。而窗口內的字符通過Set來存儲，判重通過Set的contains方法，獲取最大值通過Math的max方法來操作。

最后，此算法的時間復雜度為O(n)，其中n是字符串的長度。左指針和右指針分別會遍歷整個字符串一次。

小結

本篇文章我們重點學習的應該是滑動窗口的原理及步驟，當掌握了滑動窗口的知識之后，LeetCode的題只不過是對滑動窗口的一個示例而已。對于算法題，千萬不要死記硬背解題代碼。

最后，應不少粉絲的要求，終于組建了技術交流群，想多認識一些人，想多一些技術交流的朋友，可掃碼加入，如果超過上限，則加我微信好友，拉你入群。