Go 常見算法面試題篇(三):高效調(diào)整數(shù)組數(shù)值順序
題目
今天來(lái)看一個(gè)考察程序員基本功的數(shù)組面試題,看起來(lái)仍然很簡(jiǎn)單,不過(guò)通過(guò)這個(gè)題目的不同解法,可以快速檢驗(yàn)?zāi)闶浅跫?jí)程序員還是資深程序員,一起來(lái)看下吧:
輸入一個(gè)整數(shù)數(shù)組,實(shí)現(xiàn)一個(gè)函數(shù)來(lái)調(diào)整該數(shù)組中數(shù)字的順序,使得所有奇數(shù)位于數(shù)組的前半部分,所有偶數(shù)位于數(shù)組的后半部分。
解法一
對(duì)于新人而言,可以很快寫出下面這樣的實(shí)現(xiàn)代碼:
func reOrderArrayV1(arr []int) []int {
var oddArr, evenArr []int
for _, value := range arr {
if value % 2 == 0 {
evenArr = append(evenArr, value)
} else {
oddArr = append(oddArr, value)
}
}
return append(oddArr, evenArr...)
}
非常簡(jiǎn)單,先聲明兩個(gè)數(shù)組切片,分別用于存儲(chǔ)奇數(shù)和偶數(shù),然后遍歷待排序的數(shù)組切片,根據(jù)是否可以被 2 整除將切片數(shù)據(jù)分發(fā)到偶數(shù)和奇數(shù)切片,最后將偶數(shù)切片數(shù)據(jù)追加到奇數(shù)切片之后作為新的切片返回。
為上面這段代碼編寫測(cè)試代碼:
func main() {
arr := []int{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
fmt.Println("排序前:", arr)
fmt.Println("排序后:", reOrderArrayV1(arr))
}
執(zhí)行之后打印結(jié)果如下,說(shuō)明代碼可以正常工作:

解法二
上面的實(shí)現(xiàn)雖然簡(jiǎn)單易懂,不過(guò)擴(kuò)展性很差,比如現(xiàn)在是按照奇偶數(shù)排序,如果換一下排序條件,變成按照是否可以被3整除,或者按照正負(fù)數(shù)進(jìn)行排序,則需要重寫整個(gè)排序方法實(shí)現(xiàn)代碼。
實(shí)現(xiàn)相同功能的代碼,在滿足最基本的正確性的基礎(chǔ)上,新人和老鳥的區(qū)別往往就是體現(xiàn)在擴(kuò)展性、魯棒性、高性能這些更高層級(jí)的代碼藝術(shù)上。
下面我們從擴(kuò)展性的角度出發(fā),將排序條件抽取出來(lái)作為可定制的閉包參數(shù)從外部傳入排序函數(shù):
// 根據(jù)指定閉包對(duì)數(shù)組切片排序
func reOrderArrayV2(arr []int, orderFunc func(int) bool) []int {
// 小于等于1個(gè)元素?zé)o需處理
if arr == nil || len(arr) <= 1 {
return arr
}
// 設(shè)置兩個(gè)指針,從頭尾往中間移動(dòng)
i := 0
j := len(arr) - 1
// 頭指針不能越過(guò)尾指針,否則退出
// 以奇偶數(shù)排序?yàn)槔琲 從左到右尋找偶數(shù),j 從右到左尋找奇數(shù)
// 該循環(huán)執(zhí)行完畢后,i == j,且 i 左側(cè)的都是奇數(shù),j 右側(cè)的都是偶數(shù),也就完成了順序調(diào)整
for i < j {
// 如果不符合條件,則頭指針后移,否則中斷
// 以 orderFunc 為偶數(shù)判斷函數(shù)為例,返回 false 表示是奇數(shù)
// 題目要求奇數(shù)排在前面,因此,當(dāng) i 對(duì)應(yīng)值是奇數(shù)時(shí),往后移一位,然后繼續(xù)下一個(gè)循環(huán),直到 i==j 或者遇到第一個(gè)偶數(shù)中斷
for i < j && !orderFunc(arr[i]) {
i++
}
// 如果符合條件,則尾指針前移,否則中斷
// 還是以 orderFunc 為偶數(shù)判斷函數(shù)為例,返回 true 表示是偶數(shù)
// 題目要求偶數(shù)排在后面,因此,當(dāng) j 對(duì)應(yīng)值是偶數(shù)時(shí),往前移一位,然后繼續(xù)下一個(gè)循環(huán),直到 j==i 或者遇到第一個(gè)奇數(shù)中斷
for i < j && orderFunc(arr[j]) {
j--
}
// 如果 i < j,則交換對(duì)應(yīng)值的位置
// 以奇偶數(shù)為例,此時(shí) arr[i] 是偶數(shù),arr[j] 是奇數(shù),則交換兩個(gè)值,將奇數(shù)放到前面,偶數(shù)放到后面
if i < j {
arr[i], arr[j] = arr[j], arr[i]
}
// 繼續(xù)下一個(gè)循環(huán),直到 i==j,此時(shí) i 左側(cè)都是奇數(shù),j 右側(cè)都是偶數(shù),所有奇數(shù)都排到了偶數(shù)前面
}
return arr
}
// 排序條件:是否是偶數(shù)
func isEven(num int) bool {
return num & 1 == 0
}
這樣一來(lái),reOrderArrayV2 函數(shù)就與具體的排序條件解耦了,我們可以通過(guò)外部參數(shù)傳入任意的排序條件:
arr := []int{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
fmt.Println("排序前:", arr)
fmt.Println("排序后:", reOrderArrayV2(arr, isEven))
打印結(jié)果如下,表明排序成功:

下次你想通過(guò)正負(fù)數(shù)、是否可以被3整除之類的排序條件做排序,只需要編寫對(duì)應(yīng)的排序條件判定函數(shù),然后傳入 reOrderArrayV2排序函數(shù)即可,排序函數(shù)本身無(wú)需做任何調(diào)整:
// 是否是整數(shù)(為 true 的值放在后面)
func isPositive(num int) bool {
return num > 0
}
// 是否可以被 3 整除(為 true 的值放在后面)
func canBeDividedBy3(num int) bool {
return num % 3 == 0
}
性能對(duì)比
從擴(kuò)展性上看,顯然第二種解法比第一種好很多,除此之外,我們?cè)诘诙N解法中還通過(guò)指針移動(dòng)和位運(yùn)算的方式優(yōu)化了程序的性能,具體對(duì)性能的影響如何,可以編寫基準(zhǔn)測(cè)試來(lái)驗(yàn)證:
package main
import (
"testing"
)
func BenchmarkReOrderArrayV1(b *testing.B) {
for n := 0; n < b.N; n++ {
arr := []int{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
reOrderArrayV1(arr) // run reOrderArrayV1(arr) b.N times
}
}
func BenchmarkReOrderArrayV2(b *testing.B) {
for n := 0; n < b.N; n++ {
arr := []int{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
reOrderArrayV2(arr, isEven) // run reOrderArrayV2(arr, isEven) b.N times
}
}
運(yùn)行上面的基準(zhǔn)測(cè)試代碼:
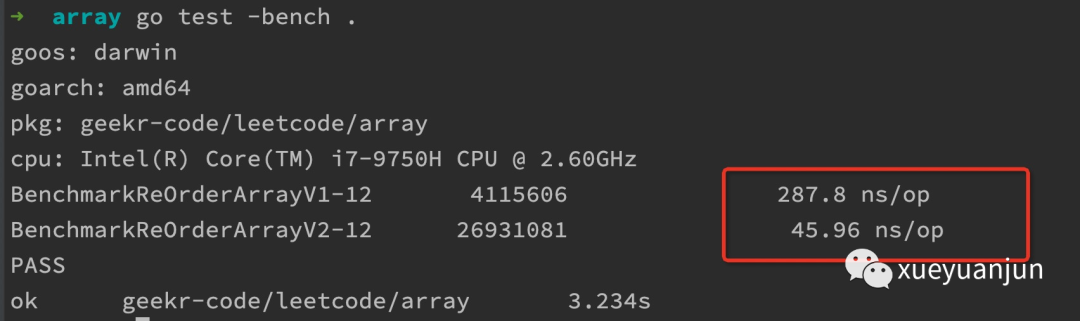
可以看到 reOrderArrayV2 排序函數(shù)的單次運(yùn)行時(shí)間要比 reOrderArrayV1 快 6 倍,性能有了很顯著的提升。
此外,還可以加上 -benchmem 選項(xiàng)對(duì)比下兩種解法的內(nèi)存分配情況(空間復(fù)雜度),由于第一種解法需要引入額外的數(shù)組切片存儲(chǔ)中間數(shù)據(jù),所以顯然第二種解法的空間復(fù)雜度更優(yōu):
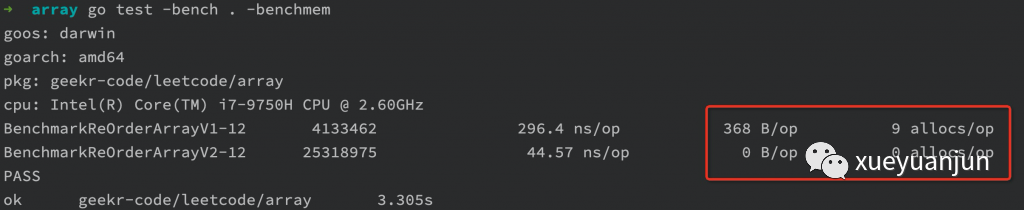
可以看到,第一種解法每次要分配 368B 的內(nèi)存空間,而第二種解法不需要額外分配內(nèi)存空間。
通過(guò)上面的對(duì)比,你覺得自己是初級(jí)程序員還是資深程序員呢?或者你還有沒有更優(yōu)的解法呢?歡迎通過(guò)下面的評(píng)論框展示你的能力。
推薦閱讀
