布隆，牛逼！布谷鳥，牛逼！

這是why的第?86?篇原創(chuàng)文章

在早期文章里面我曾經(jīng)寫過布隆過濾器：

哎，這糟糕透頂?shù)呐虐妫谎噪y盡.......

其實寫文章和寫代碼一樣。

看到一段辣眼睛的代碼，正想口吐芬芳：這是哪個煞筆寫的代碼？

結(jié)果定睛一看，代碼上寫的作者居然是自己。

甚至還不敢相信，還要打開看一下 git 的提交記錄。

發(fā)現(xiàn)確實是自己幾個月前親手敲出來，并且提交的代碼。

于是默默的改掉。

出現(xiàn)這種情況我也常常安慰自己：沒事，這是好事啊，說明我在進(jìn)步。

好了，說正事。

當(dāng)時的文章里面我說布隆過濾器的內(nèi)部原理我說不清楚。

其實我只是懶得寫而已，這玩意又不復(fù)雜，有啥說不清楚的？

布隆過濾器

布隆過濾器，在合理的使用場景中具有四兩撥千斤的作用，由于使用場景是在大量數(shù)據(jù)的場景下，所以這東西類似于秒殺，雖然沒有真的落地用過，但是也要說的頭頭是道。

常見于面試環(huán)節(jié)：比如大集合中重復(fù)數(shù)據(jù)的判斷、緩存穿透問題等。

先分享一個布隆過濾器在騰訊短視頻產(chǎn)品中的真實案例：

https://toutiao.io/posts/mtrvsx/preview

那么布隆過濾器是怎么做到上面的這些需求的呢？

首先，布隆過濾器并不存儲原始數(shù)據(jù)，因為它的功能只是針對某個元素，告訴你該元素是否存在而已。并不需要知道布隆過濾器里面有那些元素。

當(dāng)然，如果我們知道容器里面有哪些元素，就可以知道一個元素是否存在。

但是，這樣我們需要把出現(xiàn)過的元素都存儲下來，大數(shù)據(jù)量的情況下，這樣的存儲就非常的占用空間。

布隆過濾器是怎么做到不存儲元素，又知道一個元素是否存在呢？

說破了其實就很簡單：一個長長的數(shù)組加上幾個 Hash 算法。

在上面的示意圖中，一共有三個不同的 Hash 算法、一個長度為 10 的數(shù)組，數(shù)組里面存儲的是 bit 位，只放 0 和 1。初始為 0。

假設(shè)現(xiàn)在有一個元素 [why] ，要經(jīng)過這個布隆過濾器。

首先 [why] 分別經(jīng)過三個 Hash 算法，得出三個不同的數(shù)字。

Hash 算法可以保證得出的數(shù)字是在 0 到 9 之間，即不超過數(shù)組長度。

我們假設(shè)計算結(jié)果如下：

• Hash1(why)=1
• Hash2(why)=4
• Hash3(why)=8

對應(yīng)到圖片中就是這樣的：

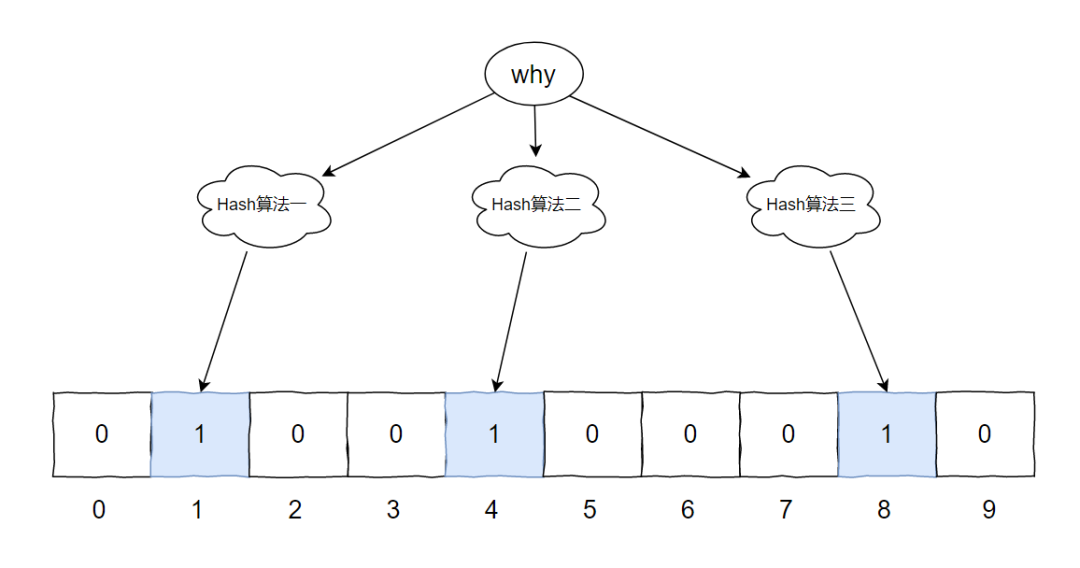
這時，如果 [why] 又來了，經(jīng)過 Hash 算法得出的下標(biāo)還是 1,4,8，發(fā)現(xiàn)數(shù)組對應(yīng)的位置上都是 1。表明這個元素極有可能出現(xiàn)過。

注意，這里說的是極有可能。也就是說會存在一定的誤判率。

我們先再存入一個元素 [jay]。

• Hash1(jay)=0
• Hash2(jay)=5
• Hash3(jay)=8

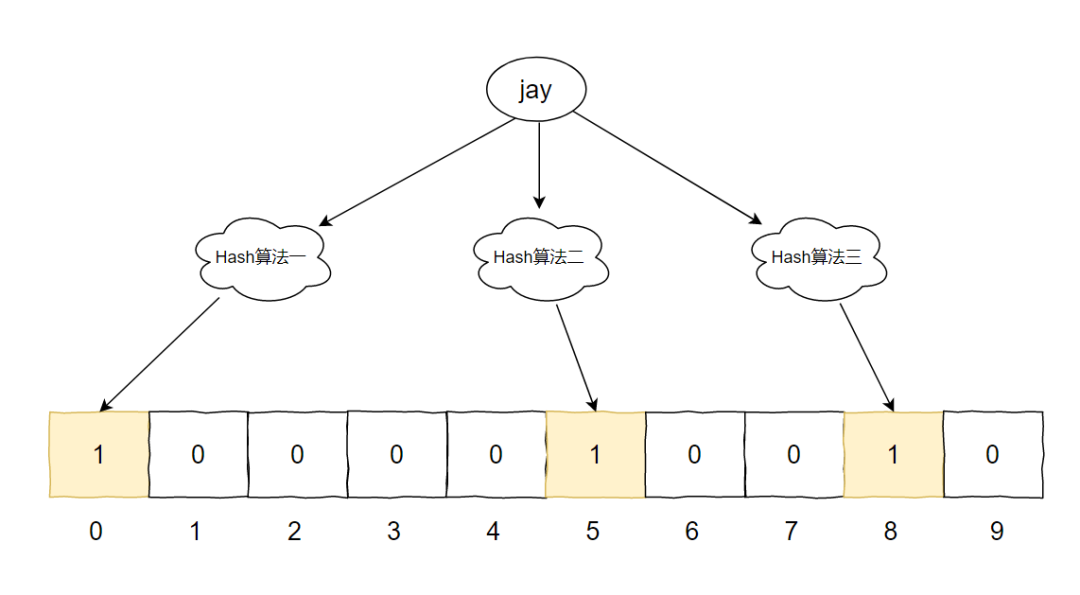
此時，我們把兩個元素匯合一下，就有了下面這個圖片：

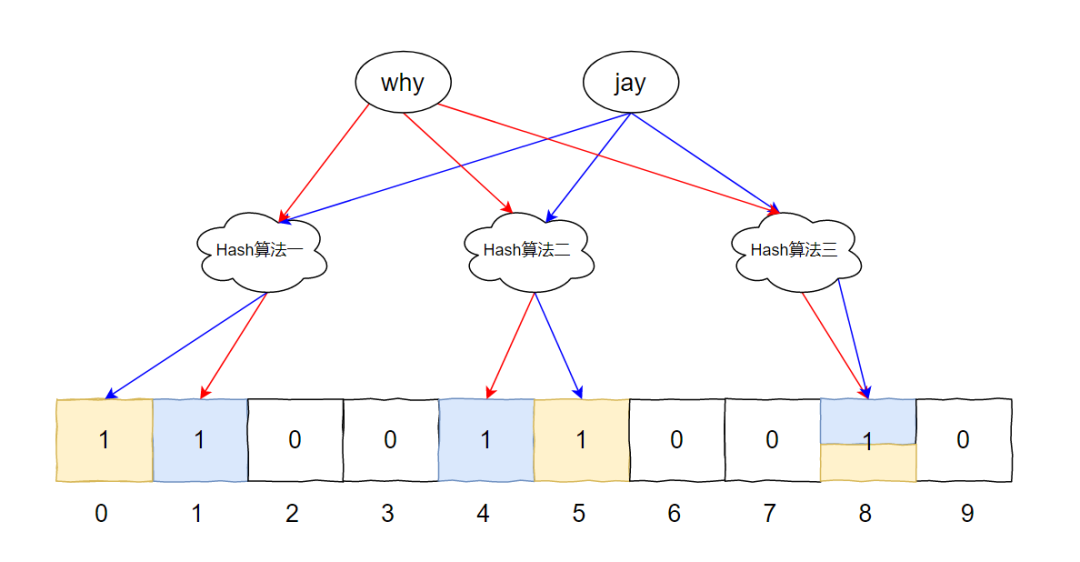
其中的下標(biāo)為 8 的位置，比較特殊，兩個元素都指向了它。

這個圖片這樣看起來有點難受，我美化一下：

好了，現(xiàn)在這個數(shù)組變成了這樣：

你說，你只看這個玩意，你能知道這個過濾器里面曾經(jīng)有過 why 和 jay 嗎？

別說你不知道了，就連過濾器本身都不知道。

現(xiàn)在，假設(shè)又來了一個元素 [Leslie]，經(jīng)過三個 Hash 算法，計算結(jié)果如下：

• Hash1(Leslie)=0
• Hash2(Leslie)=4
• Hash3(Leslie)=5

通過上面的元素，可以知道此時 0,4,5 這三個位置上都是 1。

布隆過濾器就會覺得這個元素之前可能出現(xiàn)過。于是就會返回給調(diào)用者：[Leslie]曾經(jīng)出現(xiàn)過。

但是實際情況呢？

其實我們心里門清，[Leslie] 不曾來過。

這就是誤報的情況。

這就是前面說的：布隆過濾器說存在的元素，不一定存在。

而一個元素經(jīng)過某個 hash 計算后，如果對應(yīng)位置上的值是?0，那么說明該元素一定不存在。

但是它有一個致命的缺點，就是不支持刪除。

為什么？

假設(shè)要刪除 [why]，那么就要把 1,4,8 這三個位置置為 0。

但是你想啊，[jay] 也指向了位置 8 呀。

如果刪除 [why] ，位置 8 變成了 0，那么是不是相當(dāng)于把 [jay] 也移除了？

為什么不支持刪除就致命了呢？

你又想啊，本來布隆過濾器就是使用于大數(shù)據(jù)量的場景下，隨著時間的流逝，這個過濾器的數(shù)組中為 1 的位置越來越多，帶來的結(jié)果就是誤判率的提升。從而必須得進(jìn)行重建。

所以，文章開始舉的騰訊的例子中有這樣一句話：

除了刪除這個問題之外，布隆過濾器還有一個問題：查詢性能不高。

因為真實場景中過濾器中的數(shù)組長度是非常長的，經(jīng)過多個不同 Hash 函數(shù)后，得到的數(shù)組下標(biāo)在內(nèi)存中的跨度可能會非常的大。跨度大，就是不連續(xù)。不連續(xù)，就會導(dǎo)致 CPU 緩存行命中率低。

這玩意，這么說呢。就當(dāng)八股文背起來吧。

踏雪留痕，雁過留聲，這就是布隆過濾器。

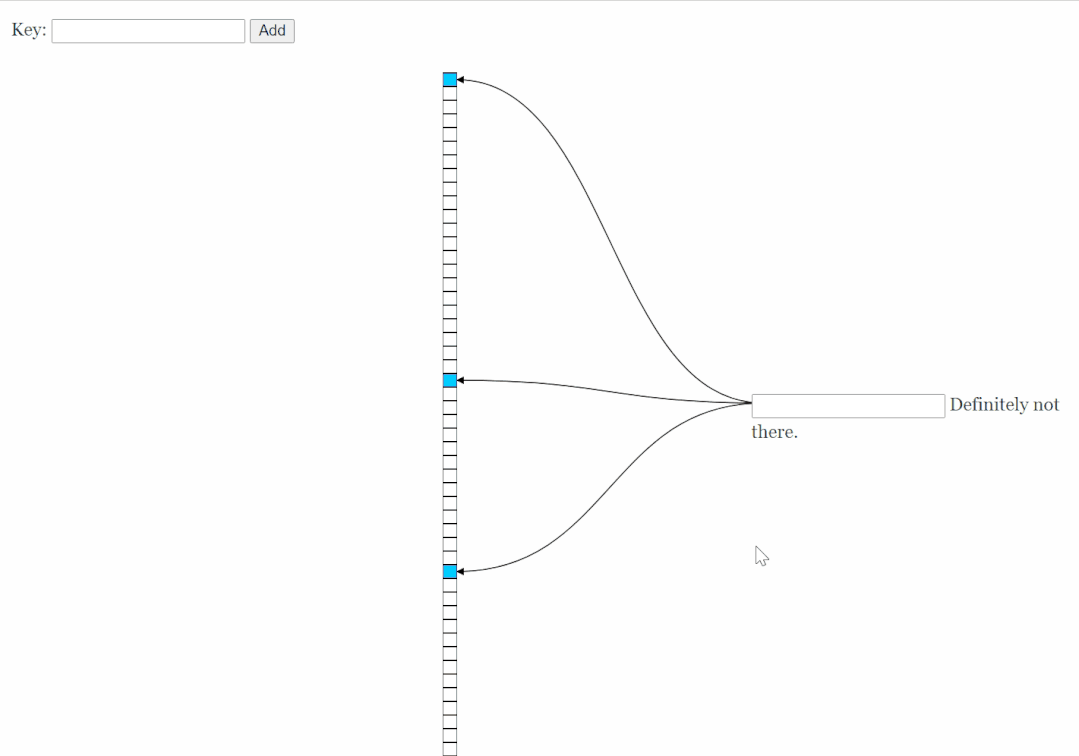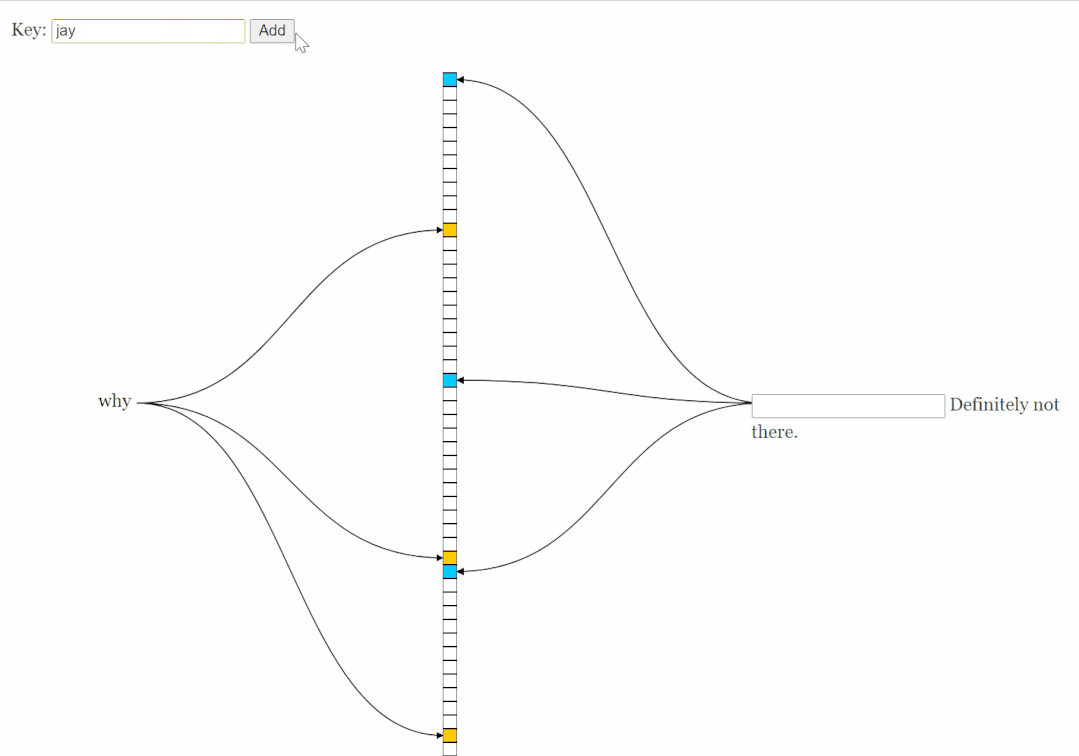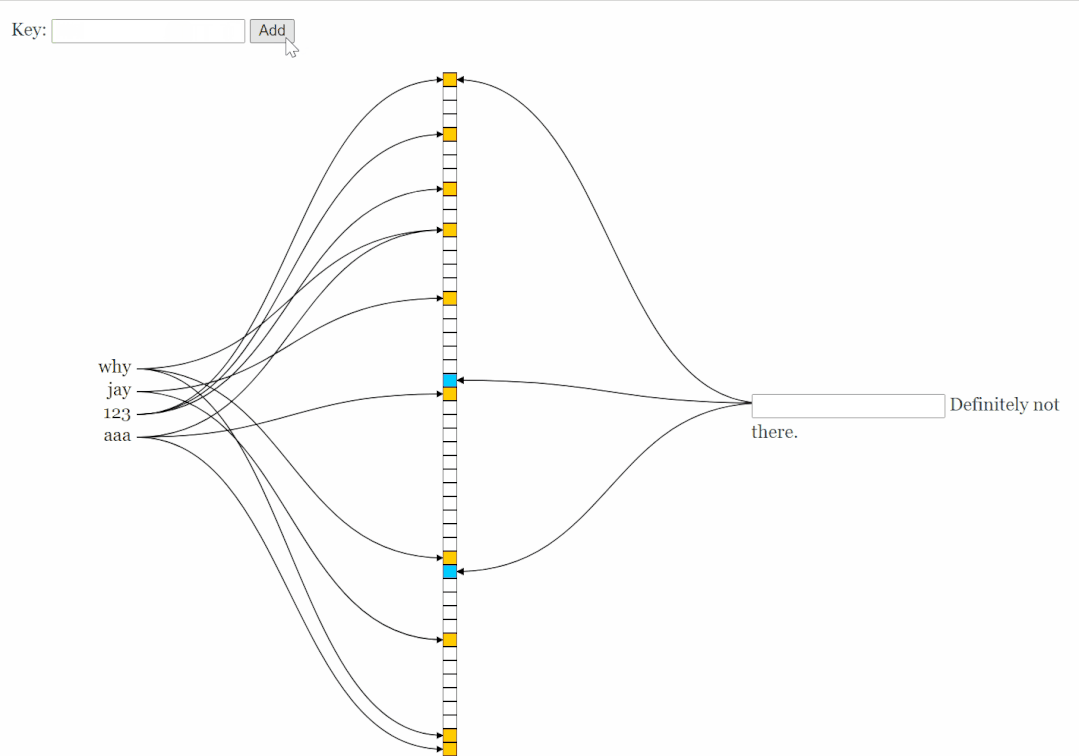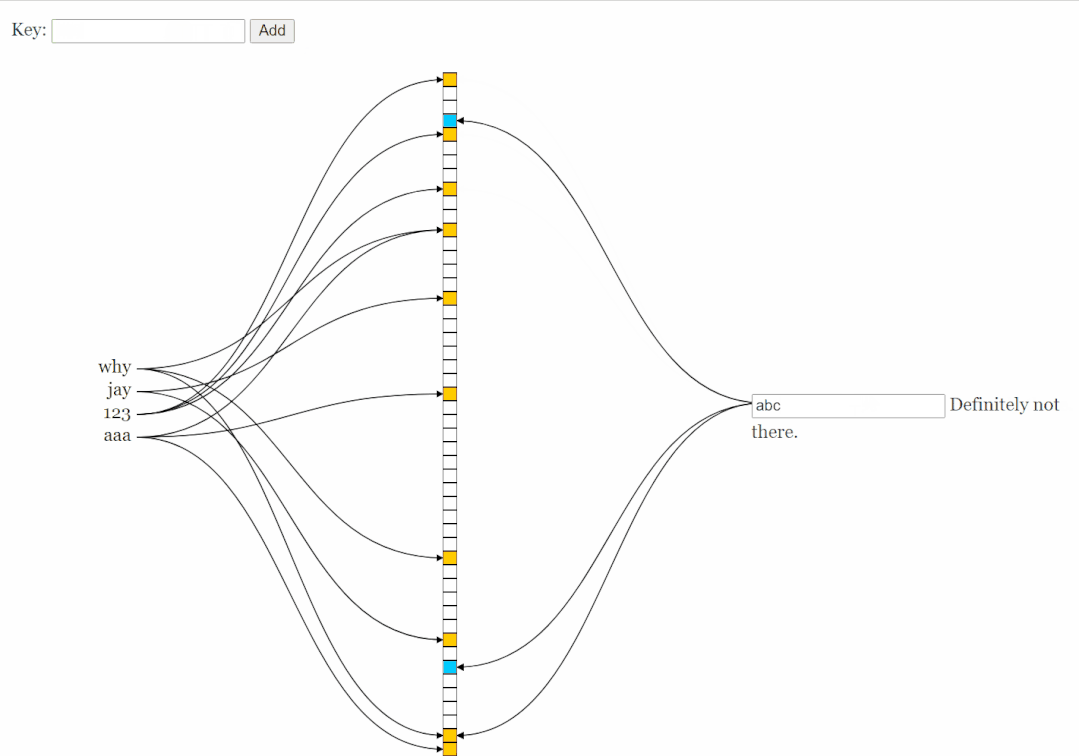
如果你想玩一下布隆過濾器，可以訪問一下這個網(wǎng)站：

https://www.jasondavies.com/bloomfilter/

左邊插入，右邊查詢：

如果要布隆過濾器支持刪除，那么怎么辦呢？

有一個叫做 Counting Bloom Filter。

它用一個 counter 數(shù)組，替換數(shù)組的比特位，這樣一比特的空間就被擴(kuò)大成了一個計數(shù)器。

用多占用幾倍的存儲空間的代價，給 Bloom Filter 增加了刪除操作。

這也是一個解決方案。

但是還有更好的解決方案，那就是布谷鳥過濾器。

另外，關(guān)于布隆過濾器的誤判率，有一個數(shù)學(xué)推理公式。很復(fù)雜，很枯燥，就不講了，有興趣的可以去了解一下。

http://pages.cs.wisc.edu/~cao/papers/summary-cache/node8.html

布谷鳥 hash

布谷鳥過濾器，第一次出現(xiàn)是在 2014 年發(fā)布的一篇論文里面：《Cuckoo Filter: Practically Better Than Bloom》

https://www.cs.cmu.edu/~dga/papers/cuckoo-conext2014.pdf

但是在講布谷鳥過濾器之前，得簡單的鋪墊一下 Cuckoo hashing，也就是布谷鳥 hash 的知識。

因為這個詞是論文的關(guān)鍵詞，在文中出現(xiàn)了 52 次之多。

Cuckoo hashing，最早出現(xiàn)在這篇 2001 年的論文之中：

https://www.cs.tau.ac.il/~shanir/advanced-seminar-data-structures-2009/bib/pagh01cuckoo.pdf

主要看論文的這個地方：

它的工作原理，總結(jié)起來是這樣的：

它有兩個 hash 表，記為 T1，T2。

兩個 hash 函數(shù)，記為 h1，h2。

當(dāng)一個不存在的元素插入的時候，會先根據(jù) h1 計算出其在 T1 表的位置，如果該位置為空則可以放進(jìn)去。

如果該位置不為空，則根據(jù) h2 計算出其在 T2 表的位置，如果該位置為空則可以放進(jìn)去。

如果該位置不為空，就把當(dāng)前位置上的元素踢出去，然后把當(dāng)前元素放進(jìn)去就行了。

也可以隨機(jī)踢出兩個位置中的一個，總之會有一個元素被踢出去。

被踢出去的元素怎么辦呢？

沒事啊，它也有自己的另外一個位置。

論文中的偽代碼是這樣的：

看不懂沒關(guān)系，我們畫個示意圖：

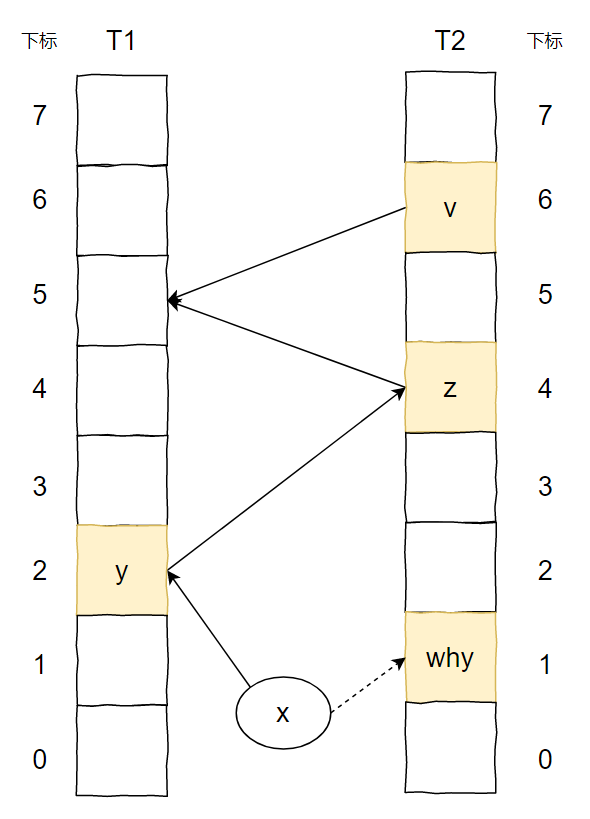
上面的圖說的是這樣的一個事兒：

我想要插入元素 x，經(jīng)過兩個 hash 函數(shù)計算后，它的兩個位置分別為 T1 表的 2 號位置和 T2 表的 1 號位置。

兩個位置都被占了，那就隨機(jī)把 T1 表 2 號位置上的 y 踢出去吧。

而 y 的另一個位置被 z 元素占領(lǐng)了。

于是 y 毫不留情把 z 也踢了出去。

z 發(fā)現(xiàn)自己的備用位置還空著（雖然這個備用位置也是元素 v 的備用位置），趕緊就位。

所以，當(dāng) x 插入之后，圖就變成了這樣：

上面這個圖其實來源就是論文里面（a）：

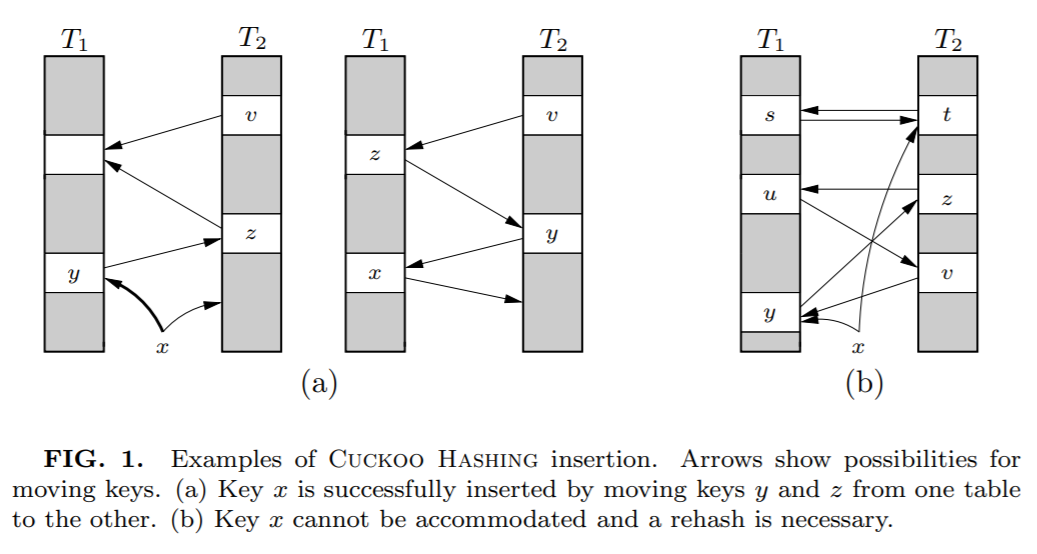
這種類似于套娃的解決方式看是可行，但是總是有出現(xiàn)循環(huán)踢出導(dǎo)致放不進(jìn) x 的問題。

比如上圖中的（b）。

當(dāng)遇到這種情況時候，說明布谷鳥 hash 已經(jīng)到了極限情況，應(yīng)該進(jìn)行擴(kuò)容，或者 hash 函數(shù)的優(yōu)化。

所以，你再次去看偽代碼的時候，你會明白里面的 MaxLoop 的含義是什么了。

這個 MaxLoop 的含義就是為了避免相互踢出的這個過程執(zhí)行次數(shù)太多，設(shè)置的一個閾值。

其實我理解，布谷鳥 hash 是一種解決 hash 沖突的騷操作。

如果你想上手玩一下，可以訪問這個網(wǎng)站：

http://www.lkozma.net/cuckoo_hashing_visualization/

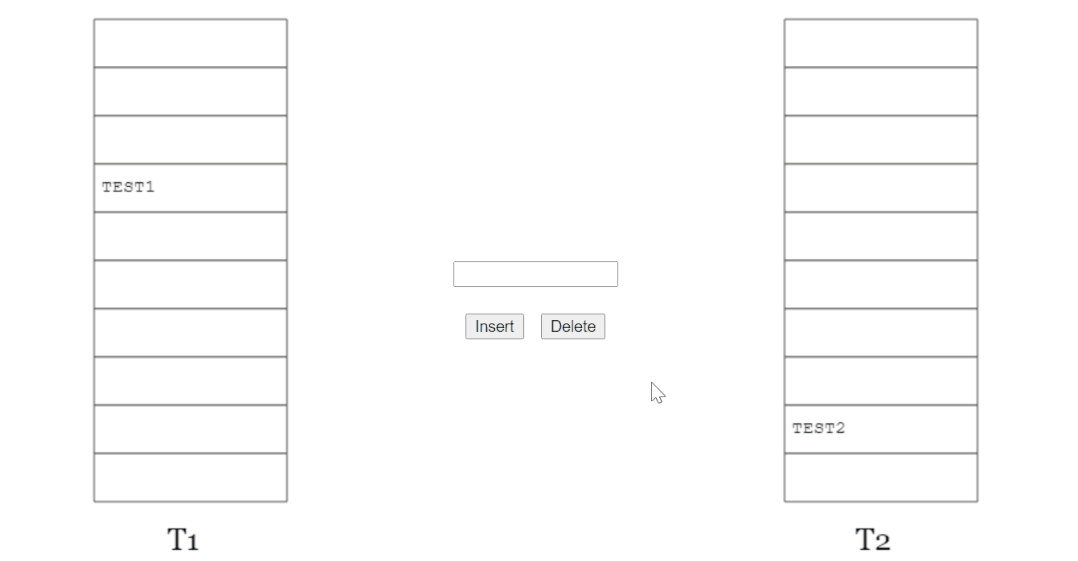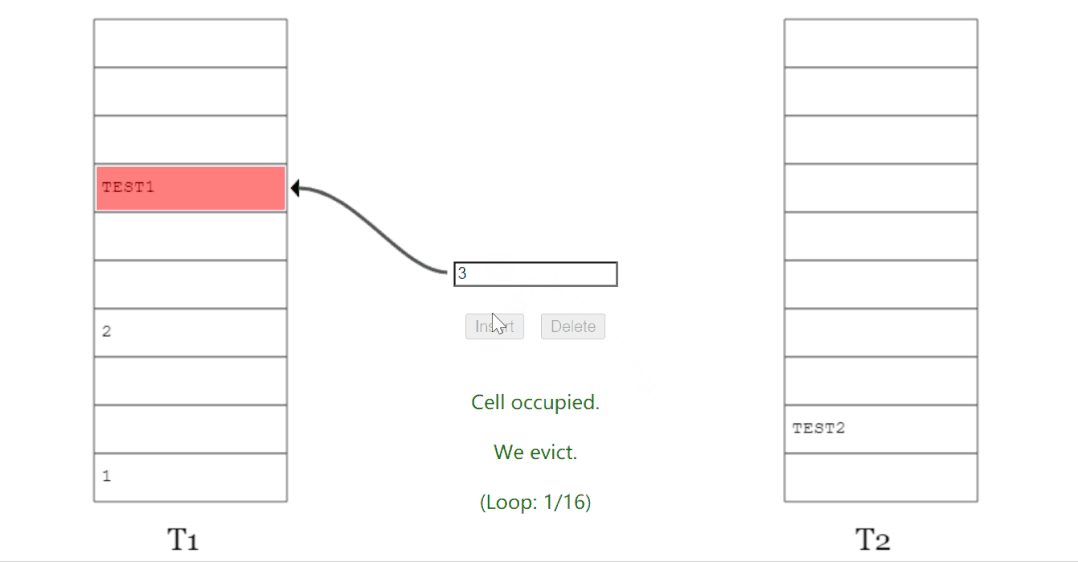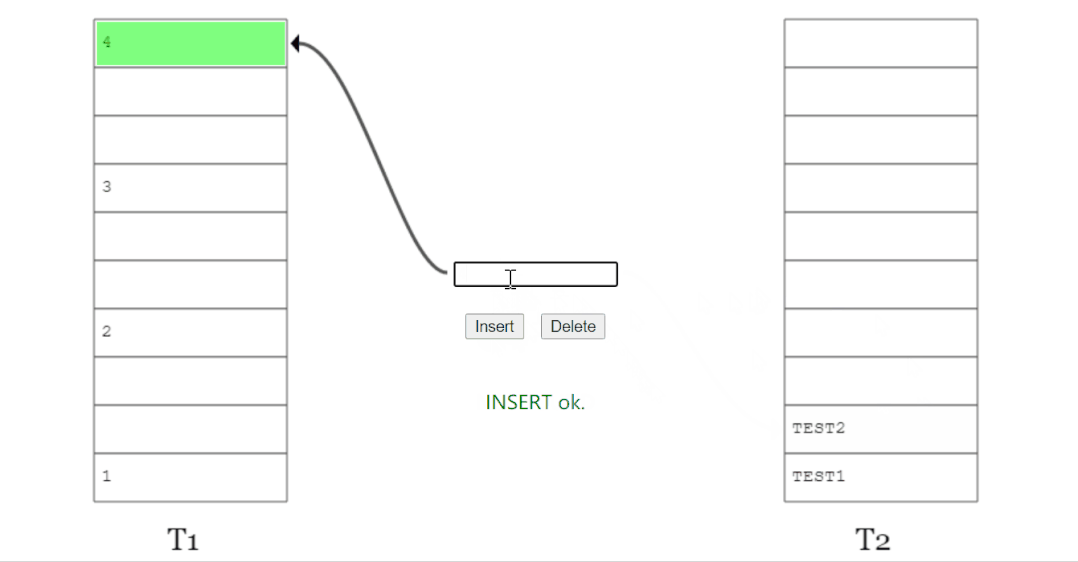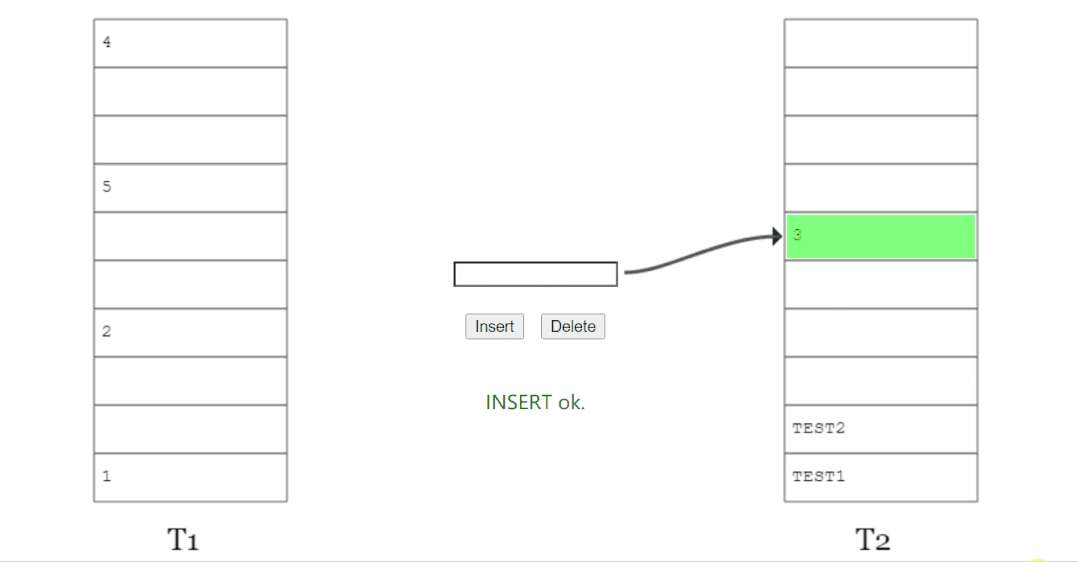
當(dāng)踢來踢去了 16 （MaxLoop）次還沒插入完成后，它會告訴你，需要 rehash 并對數(shù)組擴(kuò)容了：

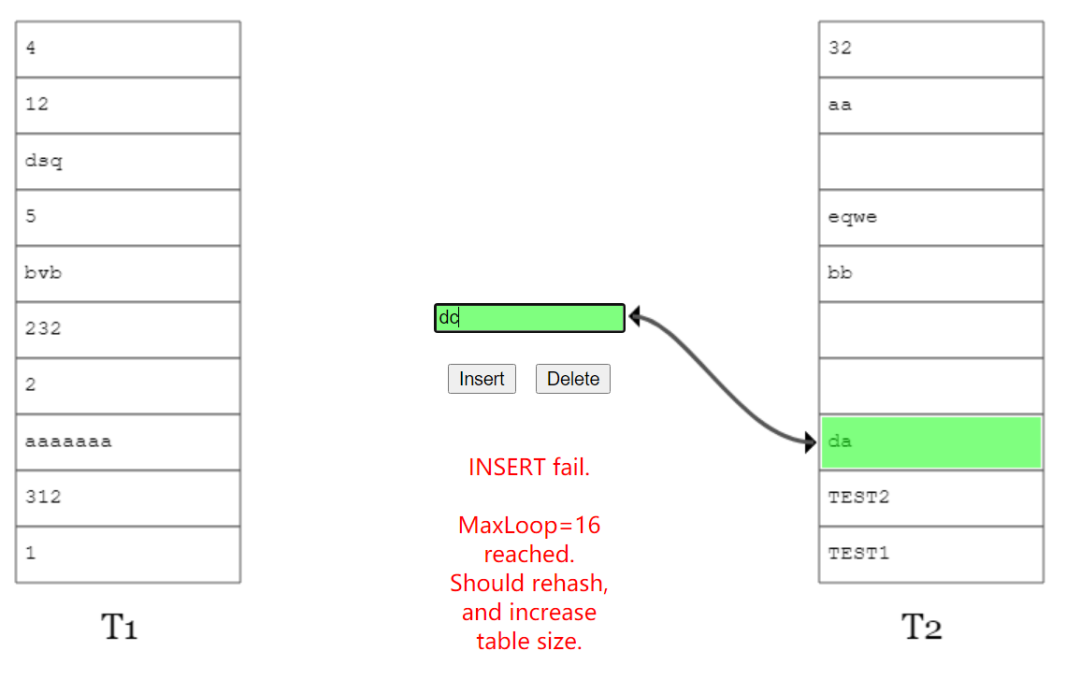
布谷鳥 hash 就是這么一回事，一場踢來踢去的游戲。

接著，我們看布谷鳥過濾器。

布谷鳥過濾器

布谷鳥過濾器的論文《Cuckoo Filter: Practically Better Than Bloom》開篇第一頁，里面有這樣一段話。

直接和布隆過濾器正面剛：我布谷鳥過濾器，就是比你屌一點。

上來就指著別人的軟肋懟：

標(biāo)準(zhǔn)的布隆過濾器的一大限制是不能刪除已經(jīng)存在的數(shù)據(jù)。如果使用它的變種，比如 Counting Bloom Filter，但是空間卻被撐大了 3 到 4 倍，巴拉巴拉巴拉......

而我就比較騷了：

這篇論文將要證明的是，與標(biāo)準(zhǔn)布隆過濾器相比，我支持刪除，在空間或性能上并不需要更高的開銷。

我，布谷鳥過濾器是一個實用的數(shù)據(jù)結(jié)構(gòu)，提供了四大優(yōu)勢：

• 1.支持動態(tài)的新增和刪除元素。
• 2.提供了比傳統(tǒng)布隆過濾器更高的查找性能，即使在空間接近滿的情況下（比如空間利用率達(dá)到 95% 的時候）。
• 3.比諸如商過濾器（quotient filter，另一種過濾器）之類的替代方案更容易實現(xiàn)。
• 4.如果要求錯誤率小于 3%，那么在許多實際應(yīng)用中，它比布隆過濾器占用的空間更小。

布谷鳥過濾器的 API 無非就是插入、查詢和刪除嘛。

其中最重要的就是插入，看一下：

論文中的部分，你大概瞟一眼，看不明白沒關(guān)系，我這不是馬上給你分析一波嗎。

插入部分的偽代碼，可以看到一點布谷鳥 hash 的影子，因為就是基于這個東西來的。

那么最大的變化在什么地方呢？

無非就是 hash 函數(shù)的變化。

看的我目瞪狗呆，心想：

首先，我們回憶一下布谷鳥 hash，它存儲的是插入元素的原始值，比如 x。

x 會經(jīng)過兩個 hash 函數(shù)，如果我們記數(shù)組的長度為 L，那么就是這樣的：

• p1 = hash1(x) % L
• p2 = hash2(x) % L

非常容易理解，是我認(rèn)知范圍內(nèi)的東西。

而布谷鳥過濾器計算位置是怎樣的呢？

• h1(x) = hash(x),
• h2(x) = h1(x) ⊕ hash(x’s fingerprint).

我們可以看到，計算 h2（位置2）時，對 x 的 fingerprint 進(jìn)行了一個 hash 計算。

“指紋”的概念一會再說，我們先關(guān)注位置的計算。

這題就稍微有點超綱了，我慢慢說。

上面算法中的異或運算確保了一個重要的性質(zhì)：位置 h2 可以通過位置 h1 和 h1 中存儲的“指紋”計算出來。

說人話就是：只要我們知道一個元素的位置（h1）和該位置里面存儲的“指紋”信息，那么我們就可以知道該“指紋”的備用位置（h2）。

因為使用的異或運算，所以這兩個位置具有對偶性。

由于具有對偶性，那么其實我們只要知道其中的任意一個位置，就能知道對應(yīng)的另外一個位置。

只要保證 hash(x’s fingerprint) !=0，那么就可以確保 h2!=h1，也就可以確保不會出現(xiàn)自己踢自己的死循環(huán)問題。

另外，為什么要對“指紋”進(jìn)行一個 hash 計算之后，在進(jìn)行異或運算呢？

論文中給出了一個反證法：如果不進(jìn)行 hash 計算，假設(shè)“指紋”的長度是 8bit，那么其對偶位置算出來，距離當(dāng)前位置最遠(yuǎn)也才 256。

為啥，論文里面寫了：

因為如果“指紋”的長度是 8bit，那么異或操作只會改變當(dāng)前位置 h1(x) 的低 8 位，高位不會改變。

就算把低 8 位全部改了，算出來的位置也就是我剛剛說的：最遠(yuǎn) 256 位。

所以，對“指紋”進(jìn)行哈希處理可確保被踢出去的元素，可以重新定位到哈希表中完全不同的存儲桶中，從而減少哈希沖突并提高表利用率。

然后這個 hash 函數(shù)還有個問題你發(fā)現(xiàn)了沒？

它沒有對數(shù)組的長度進(jìn)行取模，那么它怎么保證計算出來的下標(biāo)一定是落在數(shù)組中的呢？

這個就得說到布谷鳥過濾器的另外一個限制了。

其強(qiáng)制數(shù)組的長度必須是 2 的指數(shù)倍。

2 的指數(shù)倍的二進(jìn)制一定是這樣的：10000000...（n個0）。

這個限制帶來的好處就是，進(jìn)行異或運算時，可以保證計算出來的下標(biāo)一定是落在數(shù)組中的。

這個限制帶來的壞處就是：

• 布谷鳥過濾器：我支持刪除操作。
• 布隆過濾器：我不需要限制長度為 2 的指數(shù)倍。
• 布谷鳥過濾器：我查找性能比你高。
• 布隆過濾器：我不需要限制長度為 2 的指數(shù)倍。
• 布谷鳥過濾器：我空間利用率也高。
• 布隆過濾器：我不需要限制長度為 2 的指數(shù)倍。
• 布谷鳥過濾器：我煩死了，TMD！

接下來，說一下“指紋”。

這是論文中第一次出現(xiàn)“指紋”的地方。

“指紋”其實就是插入的元素進(jìn)行一個 hash 計算，而 hash 計算的產(chǎn)物就是幾個 bit 位。

布谷鳥過濾器里面存儲的就是元素的“指紋”。

查詢數(shù)據(jù)的時候，就是看看對應(yīng)的位置上有沒有對應(yīng)的“指紋”信息：

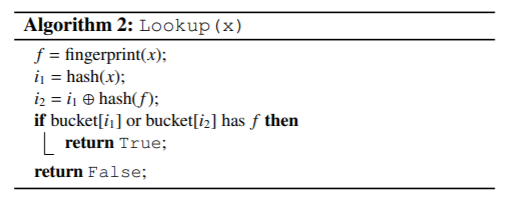
刪除數(shù)據(jù)的時候，也只是抹掉該位置上的“指紋”而已：

由于是對元素進(jìn)行 hash 計算，那么必然會出現(xiàn) hash 碰撞的問題，也就是“指紋”相同的情況，也就是會出現(xiàn)誤判的情況。

沒有存儲原數(shù)據(jù)，所以犧牲了數(shù)據(jù)的準(zhǔn)確性，但是只保存了幾個 bit，因此提升了空間效率。

說到空間利用率，你想想布谷鳥 hash 的空間利用率是多少？

在完美的情況下，也就是沒有發(fā)生哈希沖突之前，它的空間利用率最高只有 50%。

因為沒有發(fā)生沖突，說明至少有一半的位置是空著的。

除了只存儲“指紋”，布谷鳥過濾器還能怎么提高它的空間利用率的呢？

看看論文里面怎么說的：

前面的 (a)、(b) 很簡單，還是兩個 hash 函數(shù)，但是沒有用兩個數(shù)組來存數(shù)據(jù)，就是基于一維數(shù)組的布谷鳥 hash ，核心還是踢來踢去，不多說了。

重點在于 (c)，對數(shù)組進(jìn)行了展開，從一維變成了二維。

每一個下標(biāo)，可以放 4 個元素了。

你可以理解為之前一個下標(biāo)是一個圓板凳，上面只能放一個屁股。

而現(xiàn)在你可以把一個下標(biāo)看成一個四方桌，可以坐四個人，打麻將了。

這樣一個小小的轉(zhuǎn)變，空間利用率從 50% 直接到了 98%：

我就問你怕不怕？

上面截圖的論文中的第一點就是在陳訴這樣一個事實：

當(dāng) hash 函數(shù)固定為 2 個的時候，如果一個下標(biāo)只能放一個元素，那么空間利用率是 50%。

但是如果一個下標(biāo)可以放 2，4，8 個元素的時候，空間利用率就會飆升到 84%，95%，98%。

到這里，我們明白了布谷鳥過濾器對布谷鳥 hash 的優(yōu)化點和對應(yīng)的工作原理。

看起來一切都是這么的完美。

各項指標(biāo)都比布隆過濾器好，主打的是支持刪除的操作。

但是真的這么好嗎？

當(dāng)我看到論文第六節(jié)的這一段的時候，沉默了：

對重復(fù)數(shù)據(jù)進(jìn)行限制：如果需要布谷鳥過濾器支持刪除，它必須知道一個數(shù)據(jù)插入過多少次。不能讓同一個數(shù)據(jù)插入 kb+1 次。其中 k 是 hash 函數(shù)的個數(shù)，b 是一個下標(biāo)的位置能放幾個元素。

比如 2 個 hash 函數(shù)，一個二維數(shù)組，它的每個下標(biāo)最多可以插入 4 個元素。那么對于同一個元素，最多支持插入 8 次。

例如下面這種情況：

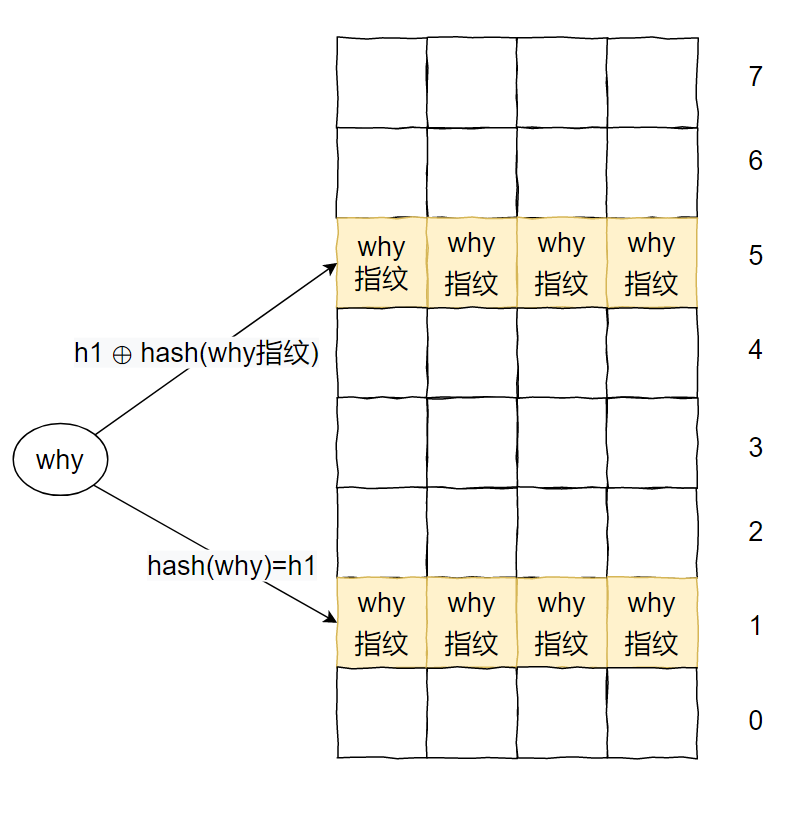
why 已經(jīng)插入了 8 次了，如果再次插入一個 why，則會出現(xiàn)循環(huán)踢出的問題，直到最大循環(huán)次數(shù)，然后返回一個 false。

怎么避免這個問題呢？

我們維護(hù)一個記錄表，記錄每個元素插入的次數(shù)就行了。

雖然邏輯簡單，但是架不住數(shù)據(jù)量大呀。你想想，這個表的存儲空間又怎么算呢？

想想就難受。

如果你要用布谷鳥過濾器的刪除操作，那么這份難受，你不得不承受。

最后，再看一下各個類型過濾器的對比圖吧：

還有，其中的數(shù)學(xué)推理過程，不說了，看的眼睛疼，而且看這玩意容易掉頭發(fā)。

荒腔走板

你知道為什么叫做“布谷鳥”嗎？

布谷鳥，又叫杜鵑。

《本草綱目》有這樣的記載：“鸤鳩不能為巢，居他巢生子”。這里描述的就是杜鵑的巢寄生行為。巢寄生指的是鳥類自己不筑巢，把卵產(chǎn)在其他種類鳥類的巢中，由宿主代替孵化育雛的繁殖方式，包括種間巢寄生（寄生者和宿主為不同物種）和種內(nèi)巢寄生（寄生者和宿主為同一物種）。現(xiàn)今一萬多種鳥類中，有一百多種具有巢寄生的行為，其中最典型的就是大杜鵑。

就是說它自己把蛋下到別的鳥巢中，讓別的鳥幫它孵小雞。哦不，孵小鳥。

小杜鵑孵出來了后，還會把同巢的其他親生鳥蛋推出鳥巢，好讓母鳥專注于喂養(yǎng)它。

我的天吶，這也太殘忍了吧。

但是這個“推出鳥巢”的動作，不正和上面描述的算法是一樣的嗎？

只是我們的算法還更加可愛一點，被推出去的鳥蛋，也就是被踢出去的元素，會放到另外一個位置上去。

我查閱資料的時候，當(dāng)我知道布谷鳥就是杜鵑鳥的時候我都震驚了。

好多詩句里面都有杜鵑啊，比如我很喜歡的，唐代詩人李商隱的《錦瑟》：

錦瑟無端五十弦，一弦一柱思華年。
莊生曉夢迷蝴蝶，望帝春心托杜鵑。
滄海月明珠有淚，藍(lán)田日暖玉生煙。
此情可待成追憶，只是當(dāng)時已惘然。

自古以來。對于這詩到底是在說“悼亡”還是“自傷”的爭論就沒停止過。

但是這重要嗎？

對我來說這不重要。

重要的是，在適當(dāng)?shù)臅r機(jī)，適當(dāng)?shù)臍夥障拢貞浧疬^去的事情的時候能適當(dāng)?shù)膩砩弦痪洌骸按饲榭纱勺窇洠皇钱?dāng)時已惘然”。

而不是說：哎，現(xiàn)在想起來，很多事情沒有好好珍惜，真TM后悔。

哦，對了。

寫文章的時候我還發(fā)現(xiàn)了一件事情。

布隆過濾器是 1970 年，一個叫做 Burton Howard Bloom 的大佬提出來的東西。

我寫這些東西的時候，就想看看大佬到底長什么樣子。

但是神奇的事情發(fā)生了，我前前后后，花了幾天，墻內(nèi)墻外翻了個底朝天，居然沒有找到大佬的任何一張照片。

我的尋找，止步于發(fā)現(xiàn)了這個網(wǎng)站：

https://www.quora.com/Where-can-one-find-a-photo-and-biographical-details-for-Burton-Howard-Bloom-inventor-of-the-Bloom-filter

這個問題應(yīng)該是在 9 年前就被人問出來了，也就是 2012 年的時候：

確實是在網(wǎng)上沒有找到關(guān)于 Burton Howard Bloom 的照片。

真是一個神奇又低調(diào)的大佬。

有可能是一個傾國傾城的美男子吧。

最后說一句（求關(guān)注）

好了，看到了這里安排個“一鍵三連”（轉(zhuǎn)發(fā)、在看、點贊）吧，周更很累的，不要白嫖我，需要一點正反饋。

才疏學(xué)淺，難免會有紕漏，如果你發(fā)現(xiàn)了錯誤的地方，可以在后臺提出來，我對其加以修改。

感謝您的閱讀，我堅持原創(chuàng)，十分歡迎并感謝您的關(guān)注。

往期推薦