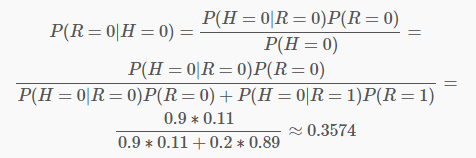貝葉斯網(wǎng)絡(luò)

數(shù)學(xué)算法俱樂部

日期 ： 2021年09月18日       

正文共 ：3424字

來源 ： 網(wǎng)絡(luò)

貝葉斯網(wǎng)絡(luò)

• 馬爾科夫鏈描述的是狀態(tài)序列，很多時(shí)候事物之間的相互關(guān)系并不能用一條鏈串起來，比如研究心血管疾病和成因之間的關(guān)系便是如此錯(cuò)綜復(fù)雜的。這個(gè)時(shí)候就要用到貝葉斯網(wǎng)絡(luò)：每個(gè)狀態(tài)只跟與之直接相連的狀態(tài)有關(guān)，而跟與它間接相連的狀態(tài)沒直接關(guān)系。但是只要在這個(gè)有向圖上，有通路連接兩個(gè)狀態(tài)，就說明這兩個(gè)狀態(tài)是有關(guān)的，可能是間接相關(guān)。狀態(tài)之間弧用轉(zhuǎn)移概率來表示，構(gòu)成了信念網(wǎng)絡(luò)（Belief Network）。
• 貝葉斯網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu)比馬爾可夫鏈靈活，不受馬爾科夫鏈的鏈狀結(jié)構(gòu)的約束，更準(zhǔn)確的描述事件之間的相關(guān)性。馬爾科夫鏈?zhǔn)秦惾~斯網(wǎng)絡(luò)的一個(gè)特例，而貝葉斯網(wǎng)絡(luò)是馬爾科夫鏈的推廣。
• 拓?fù)浣Y(jié)構(gòu)和狀態(tài)之間的相關(guān)概率，對(duì)應(yīng)結(jié)構(gòu)訓(xùn)練和參數(shù)訓(xùn)練。貝葉斯網(wǎng)絡(luò)的訓(xùn)練比較復(fù)雜，從理論上講是一個(gè)NP完備問題，對(duì)于現(xiàn)在計(jì)算機(jī)是不可計(jì)算的，但對(duì)于某些具體應(yīng)用可以進(jìn)行簡(jiǎn)化并在計(jì)算機(jī)上實(shí)現(xiàn)。

對(duì)于貝葉斯學(xué)派，首先想到的就是后驗(yàn)概率公式和先驗(yàn)分布，認(rèn)為所有的變量都是隨機(jī)的，有各自的先驗(yàn)分布。我想貝葉斯網(wǎng)絡(luò)是可以幫助醫(yī)生進(jìn)行診斷決策的，前段時(shí)間研究過的compressive tracking就是采用的樸素貝葉斯分類器，我對(duì)與貝葉斯相關(guān)內(nèi)容的應(yīng)用就是從此開始有所了解的。樸素貝葉斯分類有一個(gè)限制條件，就是特征屬性必須有條件獨(dú)立或基本獨(dú)立（實(shí)際上在現(xiàn)實(shí)應(yīng)用中幾乎不可能做到完全獨(dú)立）。當(dāng)這個(gè)條件成立時(shí)，樸素貝葉斯分類法的準(zhǔn)確率是最高的，但不幸的是，現(xiàn)實(shí)中各個(gè)特征屬性間往往并不條件獨(dú)立，而是具有較強(qiáng)的相關(guān)性，這樣就限制了樸素貝葉斯分類的能力。這里討論的就是貝葉斯分類中更高級(jí)、應(yīng)用范圍更廣的一種算法——貝葉斯網(wǎng)絡(luò)（又稱貝葉斯信念網(wǎng)絡(luò)或信念網(wǎng)絡(luò)）。

一個(gè)貝葉斯網(wǎng)絡(luò)定義包括一個(gè)有向無環(huán)圖（DAG）和一個(gè)條件概率表集合。DAG中每一個(gè)節(jié)點(diǎn)表示一個(gè)隨機(jī)變量，可以是可直接觀測(cè)變量或隱藏變量，而有向邊表示隨機(jī)變量間的條件依賴；條件概率表中的每一個(gè)元素對(duì)應(yīng)DAG中唯一的節(jié)點(diǎn)，存儲(chǔ)此節(jié)點(diǎn)對(duì)于其所有直接前驅(qū)節(jié)點(diǎn)的聯(lián)合條件概率。

貝葉斯網(wǎng)絡(luò)有一條極為重要的性質(zhì)，就是我們斷言每一個(gè)節(jié)點(diǎn)在其直接前驅(qū)節(jié)點(diǎn)的值制定后，這個(gè)節(jié)點(diǎn)條件獨(dú)立于其所有非直接前驅(qū)前輩節(jié)點(diǎn)。

這個(gè)性質(zhì)很類似Markov過程。其實(shí)，貝葉斯網(wǎng)絡(luò)可以看做是Markov鏈的非線性擴(kuò)展。這條特性的重要意義在于明確了貝葉斯網(wǎng)絡(luò)可以方便計(jì)算聯(lián)合概率分布。一般情況先，多變量非獨(dú)立聯(lián)合條件概率分布有如下求取公式： 

而在貝葉斯網(wǎng)絡(luò)中，由于存在前述性質(zhì)，任意隨機(jī)變量組合的聯(lián)合條件概率分布被化簡(jiǎn)成 

其中Parents表示xi的直接前驅(qū)節(jié)點(diǎn)的聯(lián)合，概率值可以從相應(yīng)條件概率表中查到。

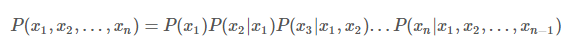
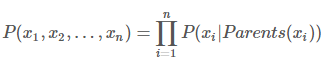
如果沒有前驅(qū)結(jié)點(diǎn)，就用先驗(yàn)概率帶入。就這樣能夠計(jì)算出所有的相關(guān)或者間接相關(guān)的變量的聯(lián)合概率密度，知道了聯(lián)合概率密度，對(duì)于邊緣概率密度的計(jì)算就非常簡(jiǎn)單了，通過這個(gè)能夠形成一些有意義的推理，等效于生成了知識(shí)。

貝葉斯網(wǎng)絡(luò)比樸素貝葉斯更復(fù)雜，而想構(gòu)造和訓(xùn)練出一個(gè)好的貝葉斯網(wǎng)絡(luò)更是異常艱難。但是貝葉斯網(wǎng)絡(luò)是模擬人的認(rèn)知思維推理模式，用一組條件概率函數(shù)以及有向無環(huán)圖對(duì)不確定性的因果推理關(guān)系建模，因此其具有更高的實(shí)用價(jià)值。

---

貝葉斯網(wǎng)絡(luò)在詞分類中的應(yīng)用

使用貝葉斯網(wǎng)絡(luò)建立一個(gè)文章、關(guān)鍵詞和概念之間的聯(lián)系。 
2002年google工程師們利用貝葉斯網(wǎng)絡(luò)建立了文章、關(guān)鍵詞和概念之間的聯(lián)系，將上百萬關(guān)鍵詞聚合成若干概念的聚類，稱之為phil cluster。最早的應(yīng)用是廣告的拓展匹配。

實(shí)際上我覺得這個(gè)應(yīng)用他講的并不清楚，我是理解不好。

不如借用《算法雜貨鋪——分類算法之貝葉斯網(wǎng)絡(luò)(Bayesian networks)》中的例子說明一下。

SNS社區(qū)中不真實(shí)賬號(hào)的檢測(cè)

在那個(gè)樸素貝葉斯分類器的解決方案中，我做了如下假設(shè)：

i、真實(shí)賬號(hào)比非真實(shí)賬號(hào)平均具有更大的日志密度、更大的好友密度以及更多的使用真實(shí)頭像。 
ii、日志密度、好友密度和是否使用真實(shí)頭像在賬號(hào)真實(shí)性給定的條件下是獨(dú)立的。

但是，上述第二條假設(shè)很可能并不成立。一般來說，好友密度除了與賬號(hào)是否真實(shí)有關(guān)，還與是否有真實(shí)頭像有關(guān)，因?yàn)檎鎸?shí)的頭像會(huì)吸引更多人加其為好友。因此，我們?yōu)榱双@取更準(zhǔn)確的分類，可以將假設(shè)修改如下：

i、真實(shí)賬號(hào)比非真實(shí)賬號(hào)平均具有更大的日志密度、更大的好友密度以及更多的使用真實(shí)頭像。 
ii、日志密度與好友密度、日志密度與是否使用真實(shí)頭像在賬號(hào)真實(shí)性給定的條件下是獨(dú)立的。 
iii、使用真實(shí)頭像的用戶比使用非真實(shí)頭像的用戶平均有更大的好友密度。

上述假設(shè)更接近實(shí)際情況，但問題隨之也來了，由于特征屬性間存在依賴關(guān)系，使得樸素貝葉斯分類不適用了。既然這樣，我去尋找另外的解決方案。

下圖表示特征屬性之間的關(guān)聯(lián)：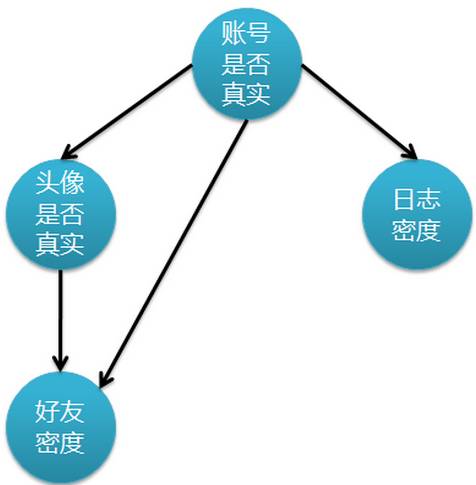 
 
上圖是一個(gè)有向無環(huán)圖，其中每個(gè)節(jié)點(diǎn)代表一個(gè)隨機(jī)變量，而弧則表示兩個(gè)隨機(jī)變量之間的聯(lián)系，表示指向結(jié)點(diǎn)影響被指向結(jié)點(diǎn)。不過僅有這個(gè)圖的話，只能定性給出隨機(jī)變量間的關(guān)系，如果要定量，還需要一些數(shù)據(jù)，這些數(shù)據(jù)就是每個(gè)節(jié)點(diǎn)對(duì)其直接前驅(qū)節(jié)點(diǎn)的條件概率，而沒有前驅(qū)節(jié)點(diǎn)的節(jié)點(diǎn)則使用先驗(yàn)概率表示。 
例如，通過對(duì)訓(xùn)練數(shù)據(jù)集的統(tǒng)計(jì)，得到下表（R表示賬號(hào)真實(shí)性，H表示頭像真實(shí)性）：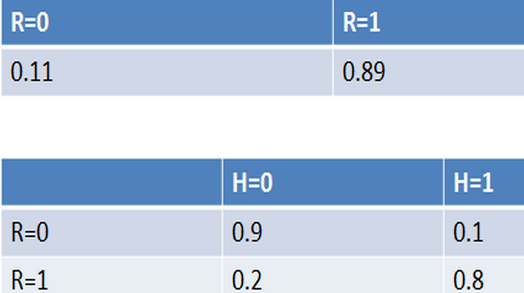 
 
縱向表頭表示條件變量，橫向表頭表示隨機(jī)變量。上表為真實(shí)賬號(hào)和非真實(shí)賬號(hào)的概率，而下表為頭像真實(shí)性對(duì)于賬號(hào)真實(shí)性的概率。這兩張表分別為“賬號(hào)是否真實(shí)”和“頭像是否真實(shí)”的條件概率表。有了這些數(shù)據(jù)，不但能順向推斷，還能通過貝葉斯定理進(jìn)行逆向推斷。例如，現(xiàn)隨機(jī)抽取一個(gè)賬戶，已知其頭像為假，求其賬號(hào)也為假的概率： 

也就是說，在僅知道頭像為假的情況下，有大約35.7%的概率此賬戶也為假。如果覺得閱讀上述推導(dǎo)有困難，請(qǐng)復(fù)習(xí)概率論中的條件概率、貝葉斯定理及全概率公式。如果給出所有節(jié)點(diǎn)的條件概率表，則可以在觀察值不完備的情況下對(duì)任意隨機(jī)變量進(jìn)行統(tǒng)計(jì)推斷。上述方法就是使用了貝葉斯網(wǎng)絡(luò)。

SNS社區(qū)中不真實(shí)賬號(hào)檢測(cè)模型中存在四個(gè)隨機(jī)變量：賬號(hào)真實(shí)性R，頭像真實(shí)性H，日志密度L，好友密度F。其中H，L，F(xiàn)是可以觀察到的值，而我們最關(guān)心的R是無法直接觀察的。這個(gè)問題就劃歸為通過H，L，F(xiàn)的觀察值對(duì)R進(jìn)行概率推理。推理過程可以如下表示：

1. 使用觀察值實(shí)例化H,L和F，把隨機(jī)值賦給R。
2. 計(jì)算P(R|H,L,F)=P(H|R)P(L|R)P(F|R,H)。其中相應(yīng)概率值可以查條件概率表。

由于上述例子只有一個(gè)未知隨機(jī)變量，所以不用迭代。更一般的，使用貝葉斯網(wǎng)絡(luò)進(jìn)行推理的步驟可如下描述：

1. 對(duì)所有可觀察隨機(jī)變量節(jié)點(diǎn)用觀察值實(shí)例化；對(duì)不可觀察節(jié)點(diǎn)實(shí)例化為隨機(jī)值。 
   
   P(y|wi)=αP(y|Parents(y))∏jP(sj|Parents(sj))
2. 對(duì)DAG進(jìn)行遍歷，對(duì)每一個(gè)不可觀察節(jié)點(diǎn)y，計(jì)算，其中wi表示除y以外的其它所有節(jié)點(diǎn)，α為正規(guī)化因子，sj表示y的第j個(gè)子節(jié)點(diǎn)。
3. 使用第三步計(jì)算出的各個(gè)y作為未知節(jié)點(diǎn)的新值進(jìn)行實(shí)例化，重復(fù)第二步，直到結(jié)果充分收斂。
4. 將收斂結(jié)果作為推斷值。 
   以上只是貝葉斯網(wǎng)絡(luò)推理的算法之一，另外還有其它算法，這里不再詳述。

---

貝葉斯網(wǎng)絡(luò)的構(gòu)造、學(xué)習(xí)訓(xùn)練

構(gòu)造與訓(xùn)練貝葉斯網(wǎng)絡(luò)分為以下兩步： 
1、確定隨機(jī)變量間的拓?fù)潢P(guān)系，形成DAG。這一步通常需要領(lǐng)域?qū)＜彝瓿桑胍⒁粋€(gè)好的拓?fù)浣Y(jié)構(gòu)，通常需要不斷迭代和改進(jìn)才可以，需要用到機(jī)器學(xué)習(xí)得到。 
2、訓(xùn)練貝葉斯網(wǎng)絡(luò)。這一步也就是要完成條件概率表的構(gòu)造，如果每個(gè)隨機(jī)變量的值都是可以直接觀察的，像我們上面的例子，那么這一步的訓(xùn)練是直觀的，方法類似于樸素貝葉斯分類。但是通常貝葉斯網(wǎng)絡(luò)的中存在隱藏變量節(jié)點(diǎn)，那么訓(xùn)練方法就是比較復(fù)雜，例如使用梯度下降法。

優(yōu)化的貝葉斯網(wǎng)絡(luò)結(jié)構(gòu)要保證它產(chǎn)生的序列從頭到尾的可能性最大，如果用概率做度量，就是后驗(yàn)概率最大。當(dāng)然可以搜索所有可能的路徑，但是會(huì)是一個(gè)NP-Hard問題。一般采用貪心算法，在每一步時(shí)沿著箭頭方向?qū)ふ矣邢薏剑澬娜菀紫萑刖植孔顑?yōu)。為防止局部最優(yōu)，采用蒙特卡洛方法，用許多隨機(jī)數(shù)在貝葉斯網(wǎng)絡(luò)中試試，看看是否陷入局部最優(yōu)，但計(jì)算量較大。最近，新的方法是利用互信息，只保留互信息較大的節(jié)點(diǎn)的直接連接，然后再對(duì)簡(jiǎn)化的網(wǎng)絡(luò)進(jìn)行完備的搜索，找到全局優(yōu)化的結(jié)構(gòu)。

而節(jié)點(diǎn)之間弧的權(quán)重確定可以通過最大后驗(yàn)估計(jì)來得到，使用EM（expectation-maximization process）過程來解決。

一般的，參數(shù)和結(jié)構(gòu)的交替訓(xùn)練的，先優(yōu)化結(jié)構(gòu)，再優(yōu)化參數(shù)，然后再優(yōu)化結(jié)構(gòu)...直至得到收斂或者誤差足夠小的模型。

---

參考文獻(xiàn)：

吳軍 《數(shù)學(xué)之美》 
張洋 《算法雜貨鋪——分類算法之貝葉斯網(wǎng)絡(luò)(Bayesian networks)》

— THE END —

?概率與隨機(jī)過程基礎(chǔ)

?京東 | AI人才聯(lián)合培養(yǎng)計(jì)劃

?人類如何感受到四維空間？

?【干貨】計(jì)算幾何常用算法

?搜索引擎技術(shù)之網(wǎng)絡(luò)爬蟲

?數(shù)學(xué)  |   小學(xué)生如何詮釋數(shù)學(xué)的線條美？