貝葉斯網絡的因果關系檢測(Python)
點擊上方“小白學視覺”,選擇加"星標"或“置頂”
重磅干貨,第一時間送達
在機器學任務中,確定變量間的因果關系(causality)可能是一個具有挑戰(zhàn)性的步驟,但它對于建模工作非常重要。本文將總結有關貝葉斯概率(Bayesian probabilistic)因果模型(causal models)的概念,然后提供一個Python實踐教程,演示如何使用貝葉斯結構學習來檢測因果關系。
1. 背景
在許多領域,如預測、推薦系統(tǒng)、自然語言處理等,使用機器學習技術已成為獲取有用觀察和進行預測的標準工具。
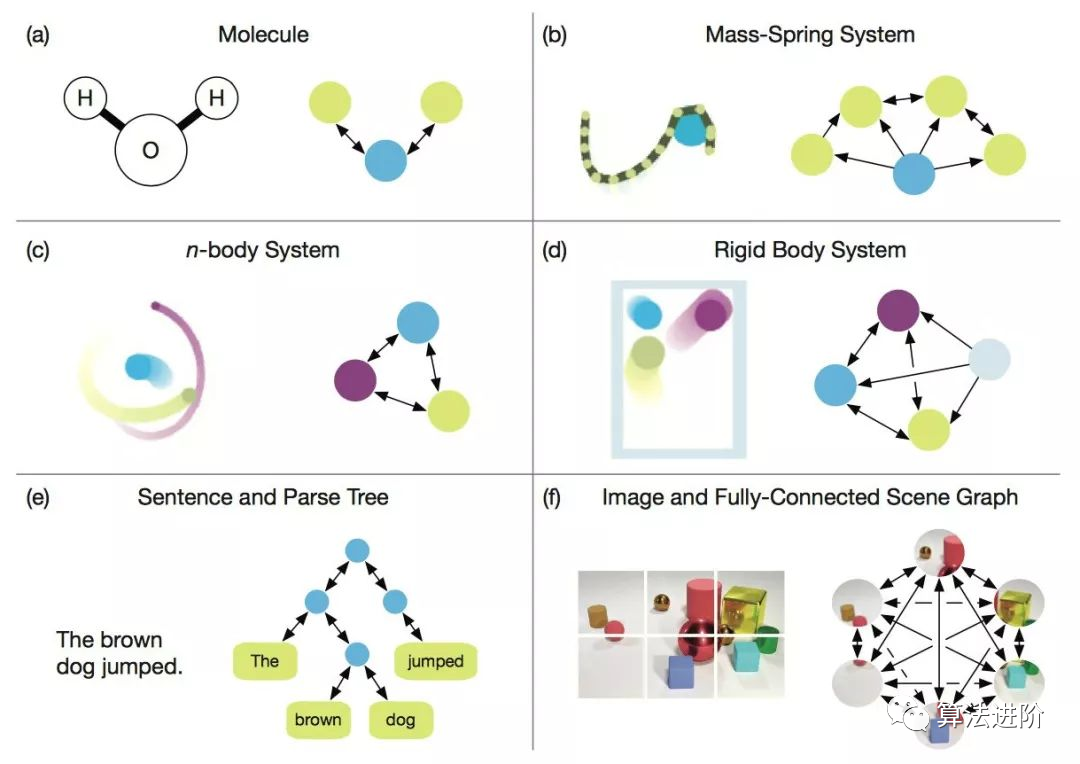
1.1. 相關性
-
正相關:兩個變量之間存在一種關系,即兩個變量同時朝同一方向移動。 -
負相關:兩個變量之間存在一種關系,即一個變量增加與另一個變量減少相關聯(lián)。 -
無相關性:當兩個變量之間沒有關系時。
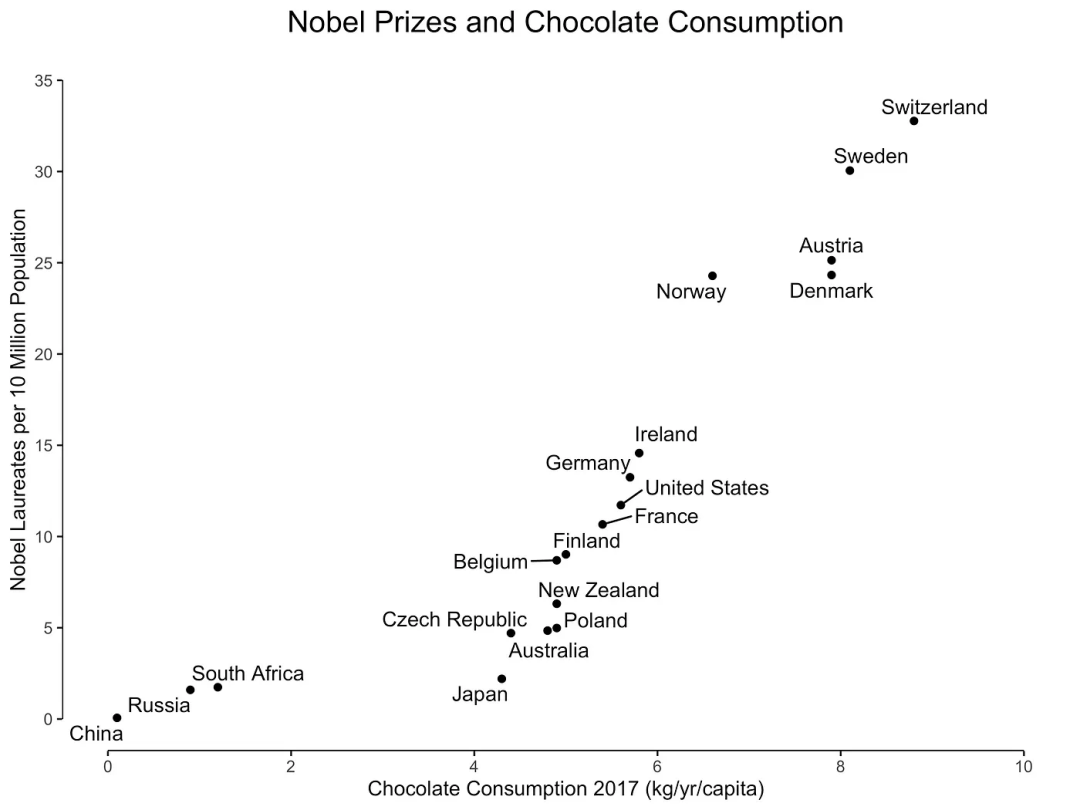
1.1.2. 關聯(lián)性
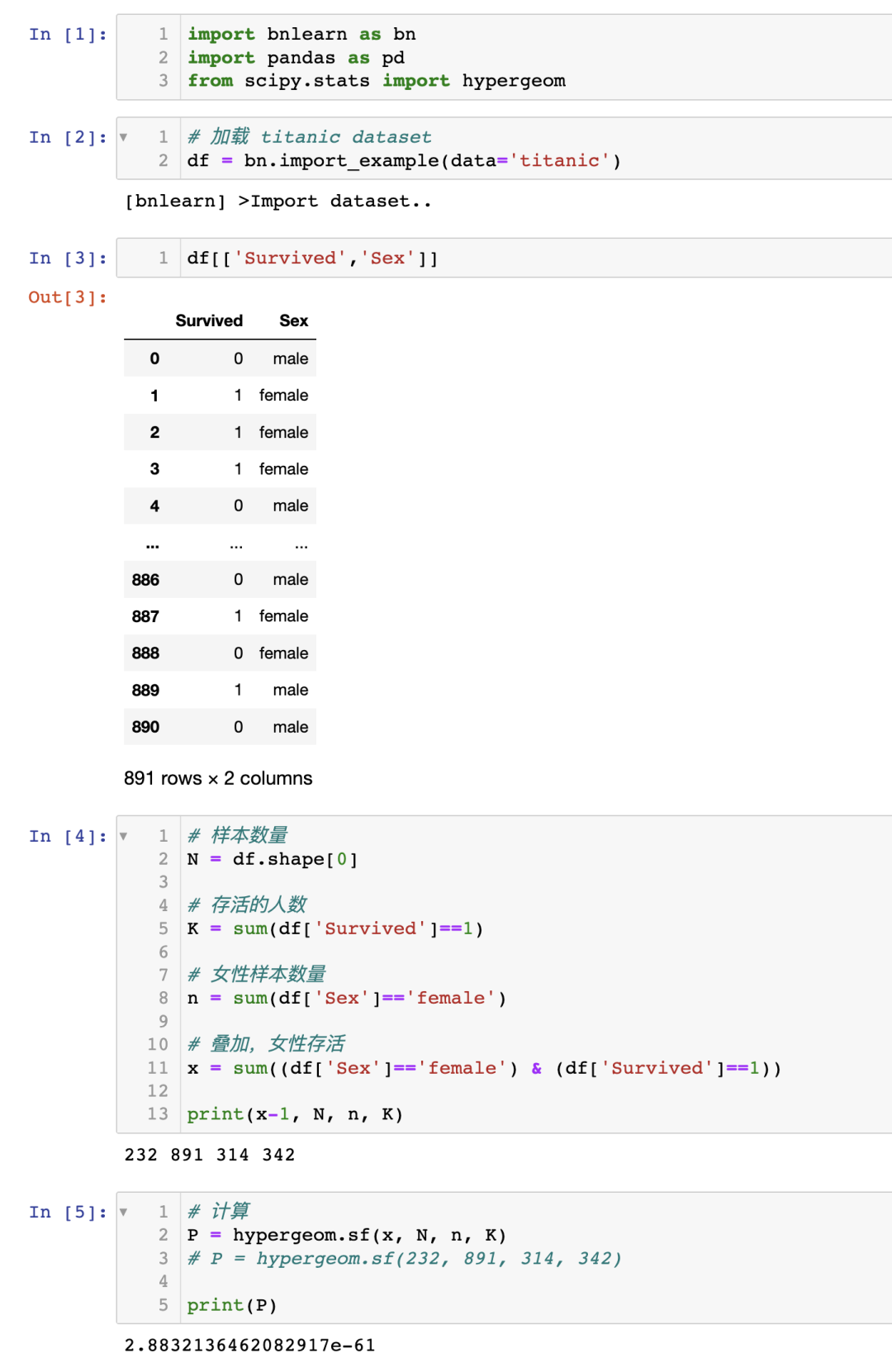

方程 1:使用超幾何檢驗測試幸存與女性之間的關聯(lián)性
2. 因果關系
如果兩個隨機變量 和 在統(tǒng)計上相關( ),那么要么(a) 導致 ,(b) 導致 ,或者(c)存在一個第三個變量 同時導致 和 。此外,給定 的條件下, 和 變得獨立,即 。
貝葉斯圖模型又稱貝葉斯網絡、貝葉斯信念網絡、Bayes Net、因果概率網絡和影響圖。都是同一技術,不同的叫法。

可以創(chuàng)建四個圖:(a、b)級聯(lián),(c)共同父節(jié)點和(d)V 結構,這些圖構成了貝葉斯網絡的基礎。
需要注意的是,貝葉斯網絡是有向無環(huán)圖(Directed Acyclic Graph, DAG),而 DAG 是具有因果性的。這意味著圖中的邊是有向的,并且沒有(反饋)循環(huán)(無環(huán))。
2.1. 概率論
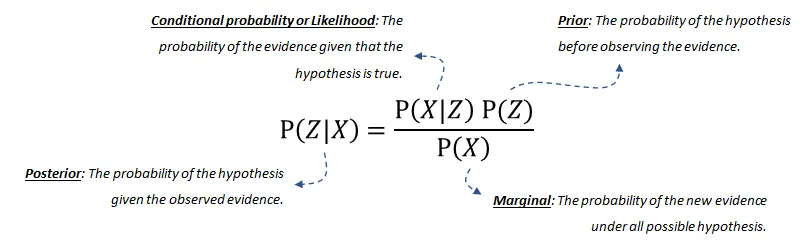
-
后驗概率(posterior probability)是給定 -
條件概率(conditional probability)或似然是在假設成立的情況下,證據發(fā)生的概率。這可以從數據中推導出來。 -
我們的先驗(prior)信念是在觀察到證據之前,假設的概率。這也可以從數據或領域知識中推導出來。 -
最后,邊際(marginal)概率描述了在所有可能的假設下新證據發(fā)生的概率,需要計算。如果您想了解更多關于(分解的)概率分布或貝葉斯網絡的聯(lián)合分布的詳細信息,請閱讀這篇博客[6]。
3. 貝葉斯結構學習用于估計 DAG
BIC是貝葉斯信息準則(Bayesian Information Criterion)的縮寫。它是一種用于模型選擇的統(tǒng)計量,可以用于比較不同模型的擬合能力。BIC值越小,表示模型越好。在貝葉斯網絡中,BIC是一種常用的評分函數之一,用于評估貝葉斯網絡與數據的擬合程度。
BDeu是貝葉斯-狄利克雷等價一致先驗(Bayesian-Dirichlet equivalent uniform prior)的縮寫。它是一種常用的評分函數之一,用于評估貝葉斯網絡與數據的擬合程度。BDeu評分函數基于貝葉斯-狄利克雷等價一致先驗,該先驗假設每個變量的每個可能狀態(tài)都是等可能的。
基于評分的結構學習
-
基于約束的結構學習
3.1. 基于評分的結構學習
-
搜索算法用于優(yōu)化所有可能的 DAG 搜索空間;例如 ExhaustiveSearch、Hillclimbsearch、Chow-Liu 等。 -
評分函數指示貝葉斯網絡與數據的匹配程度。常用的評分函數是貝葉斯狄利克雷分數,如 BDeu 或 K2,以及貝葉斯信息準則(BIC,也稱為 MDL)。
-
ExhaustiveSearch,顧名思義,對每個可能的 DAG 進行評分并返回得分最高的 DAG。這種搜索方法僅適用于非常小的網絡,并且阻止高效的局部優(yōu)化算法始終找到最佳結構。因此,通常無法找到理想的結構。然而,如果只涉及少數節(jié)點(即少于 5 個左右),啟發(fā)式搜索策略通常會產生良好的結果。 -
Hillclimbsearch 是一種啟發(fā)式搜索方法,可用于使用更多節(jié)點的情況。HillClimbSearch 實施了一種貪婪的局部搜索,從 DAG“start”(默認為斷開的 DAG)開始,通過迭代執(zhí)行最大化增加評分的單邊操作。搜索在找到局部最大值后終止。 -
Chow-Liu 算法是一種特定類型的基于樹的方法。Chow-Liu 算法找到最大似然樹結構,其中每個節(jié)點最多只有一個父節(jié)點。通過限制為樹結構,可以限制復雜性。 -
Tree-augmented Naive Bayes(TAN)算法也是一種基于樹的方法,可用于建模涉及許多不確定性的龐大數據集的各種相互依賴特征集。
3.2. 基于約束的結構學習
4. 實踐:基于bnlearn 庫
結構學習:給定數據:估計捕捉變量之間依賴關系的 DAG。
參數學習:給定數據和 DAG:估計各個變量的(條件)概率分布。
-
推斷:給定學習的模型:確定查詢的精確概率值。
基于 pgmpy 庫構建
包含最常用的貝葉斯管道
簡單直觀
開源
詳細文檔
4.1. 在灑水器數據集中進行結構學習
使用 bnlearn 庫,用幾行代碼就能確定因果關系。
請注意,灑水器數據集已經過處理,沒有缺失值,所有值都處于 1 或 0 的狀態(tài)。

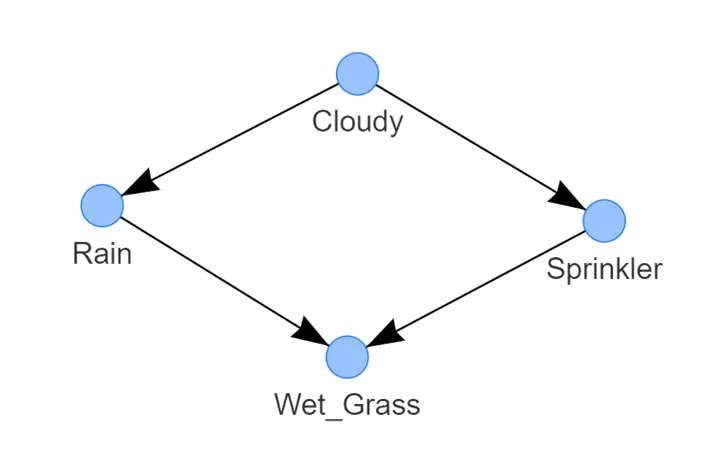
濕草的狀態(tài)取決于兩個節(jié)點,即雨水和灑水器;
雨水的狀態(tài)由多云的狀態(tài)決定;
-
而灑水器的狀態(tài)也由多云的狀態(tài)決定。
# 'hc' or 'hillclimbsearch'model_hc_bic = bn.structure_learning.fit(df, methodtype='hc', scoretype='bic')model_hc_k2 = bn.structure_learning.fit(df, methodtype='hc', scoretype='k2')model_hc_bdeu = bn.structure_learning.fit(df, methodtype='hc', scoretype='bdeu')
# 'ex' or 'exhaustivesearch'model_ex_bic = bn.structure_learning.fit(df, methodtype='ex', scoretype='bic')model_ex_k2 = bn.structure_learning.fit(df, methodtype='ex', scoretype='k2')model_ex_bdeu = bn.structure_learning.fit(df, methodtype='ex', scoretype='bdeu')
# 'cs' or 'constraintsearch'model_cs_k2 = bn.structure_learning.fit(df, methodtype='cs', scoretype='k2')model_cs_bdeu = bn.structure_learning.fit(df, methodtype='cs', scoretype='bdeu')model_cs_bic = bn.structure_learning.fit(df, methodtype='cs', scoretype='bic')
# 'cl' or 'chow-liu' (requires setting root_node parameter)model_cl = bn.structure_learning.fit(df, methodtype='cl', root_node='Wet_Grass')
如果灑水器關閉,草地濕潤的概率有多大?
如果灑水器關閉且多云,下雨的概率有多大?
4.2. 如何進行推斷?
4.2.1. 參數學習
-
最大似然估計是使用變量狀態(tài)出現的相對頻率進行的自然估計。在對貝葉斯網絡進行參數估計時,數據不足是一個常見問題,最大似然估計器存在對數據過擬合的問題。換句話說,如果觀察到的數據對于基礎分布來說不具有代表性(或者太少),最大似然估計可能會相差甚遠。例如,如果一個變量有 3 個可以取 10 個狀態(tài)的父節(jié)點,那么狀態(tài)計數將分別針對 -
貝葉斯估計從已存在的先驗 CPTs 開始,這些 CPTs 表示在觀察到數據之前我們對變量的信念。然后,使用觀察數據的狀態(tài)計數來更新這些“先驗”。可以將先驗視為偽狀態(tài)計數,在歸一化之前將其添加到實際計數中。一個非常簡單的先驗是所謂的 K2 先驗,它只是將“1”添加到每個單獨狀態(tài)的計數中。一個更明智的先驗選擇是 BDeu(貝葉斯狄利克雷等效均勻先驗)。


# Examples to illustrate how to manually compute MLE for the node Cloudy and Rain:# Compute CPT for the Cloudy Node:# This node has no conditional dependencies and can easily be computed as following:# P(Cloudy=0)sum(df['Cloudy']==0) / df.shape[0] # 0.488# P(Cloudy=1)sum(df['Cloudy']==1) / df.shape[0] # 0.512# Compute CPT for the Rain Node:# This node has a conditional dependency from Cloudy and can be computed as following:# P(Rain=0 | Cloudy=0)sum( (df['Cloudy']==0) & (df['Rain']==0) ) / sum(df['Cloudy']==0) # 394/488 = 0.807377049# P(Rain=1 | Cloudy=0)sum( (df['Cloudy']==0) & (df['Rain']==1) ) / sum(df['Cloudy']==0) # 94/488 = 0.192622950# P(Rain=0 | Cloudy=1)sum( (df['Cloudy']==1) & (df['Rain']==0) ) / sum(df['Cloudy']==1) # 91/512 = 0.177734375# P(Rain=1 | Cloudy=1)sum( (df['Cloudy']==1) & (df['Rain']==1) ) / sum(df['Cloudy']==1) # 421/512 = 0.822265625
4.2.2. 在 Sprinkler 數據集上進行推理


如果噴灌系統(tǒng)關閉,草坪潮濕的可能性有多大?P(Wet_grass=1 | Sprinkler=0) = 0.51 如果噴灌系統(tǒng)關閉并且天陰,有下雨的可能性有多大?P(Rain=1 | Sprinkler=0, Cloudy=1) = 0.663
4.3. 我如何知道我的因果模型是正確的?
5. 討論
后驗概率分布的結果或圖形使用戶能夠對模型預測做出判斷,而不僅僅是獲得單個值作為結果。
可以將領域/專家知識納入到 DAG 中,并在不完整信息和缺失數據的情況下進行推理。這是可能的,因為貝葉斯定理基于用證據更新先驗項。
具有模塊化的概念。
通過組合較簡單的部分來構建復雜系統(tǒng)。
圖論提供了直觀的高度交互的變量集。
-
概率論提供了將這些部分組合在一起的方法。
下載1:OpenCV-Contrib擴展模塊中文版教程
在「小白學視覺」公眾號后臺回復:擴展模塊中文教程,即可下載全網第一份OpenCV擴展模塊教程中文版,涵蓋擴展模塊安裝、SFM算法、立體視覺、目標跟蹤、生物視覺、超分辨率處理等二十多章內容。
下載2:Python視覺實戰(zhàn)項目52講 在「小白學視覺」公眾號后臺回復:Python視覺實戰(zhàn)項目,即可下載包括圖像分割、口罩檢測、車道線檢測、車輛計數、添加眼線、車牌識別、字符識別、情緒檢測、文本內容提取、面部識別等31個視覺實戰(zhàn)項目,助力快速學校計算機視覺。
下載3:OpenCV實戰(zhàn)項目20講 在「小白學視覺」公眾號后臺回復:OpenCV實戰(zhàn)項目20講,即可下載含有20個基于OpenCV實現20個實戰(zhàn)項目,實現OpenCV學習進階。
交流群
歡迎加入公眾號讀者群一起和同行交流,目前有SLAM、三維視覺、傳感器、自動駕駛、計算攝影、檢測、分割、識別、醫(yī)學影像、GAN、算法競賽等微信群(以后會逐漸細分),請掃描下面微信號加群,備注:”昵稱+學校/公司+研究方向“,例如:”張三 + 上海交大 + 視覺SLAM“。請按照格式備注,否則不予通過。添加成功后會根據研究方向邀請進入相關微信群。請勿在群內發(fā)送廣告,否則會請出群,謝謝理解~
評論
圖片
表情

