非常詳細(xì)的范式講解（1NF/2NF/3NF/BCNF）

范式在計(jì)算機(jī)方面運(yùn)用廣泛，在計(jì)算機(jī)二級(jí)三級(jí)均涉及到，今天就來(lái)講講范式。要是能夠認(rèn)真的看完，相信一定能夠理解的。

在講范式之前，我們先來(lái)了解有關(guān)范式的基本概念，聽(tīng)懂了有利于后面的學(xué)習(xí)。

1. 函數(shù)依賴(lài)

首先一個(gè)好的關(guān)系模式是不會(huì)出現(xiàn)以下問(wèn)題的：

1. 插入異常

2. 刪除異常

3. 更新異常

4. 數(shù)據(jù)冗余盡量少

如果出現(xiàn)那是由于 數(shù)據(jù)依賴(lài)，其中數(shù)據(jù)依賴(lài)分為：函數(shù)依賴(lài)，多值依賴(lài)，連接依賴(lài)等等。

所以，當(dāng)關(guān)系模式出現(xiàn)問(wèn)題，解決方法為—— 規(guī)范化理論（找到關(guān)系模式中不適合的數(shù)據(jù)依賴(lài)，并消除它們）

在范式這里經(jīng)常使用函數(shù)依賴(lài)。那么什么是函數(shù)依賴(lài)呢？關(guān)系R中的屬性 X，R 中的屬性 Y 只有唯一值與之對(duì)應(yīng)，則稱(chēng) X 函數(shù)決定 Y 或稱(chēng) Y 函數(shù)依賴(lài)于 X ，記作 X—>Y 。其中，X 稱(chēng)為決定因素。以下關(guān)系模型經(jīng)常簡(jiǎn)化為 R<U,F>，如下圖。

這里給出一個(gè)例子，后面就根據(jù)這個(gè)例子來(lái)講解。

非常主要

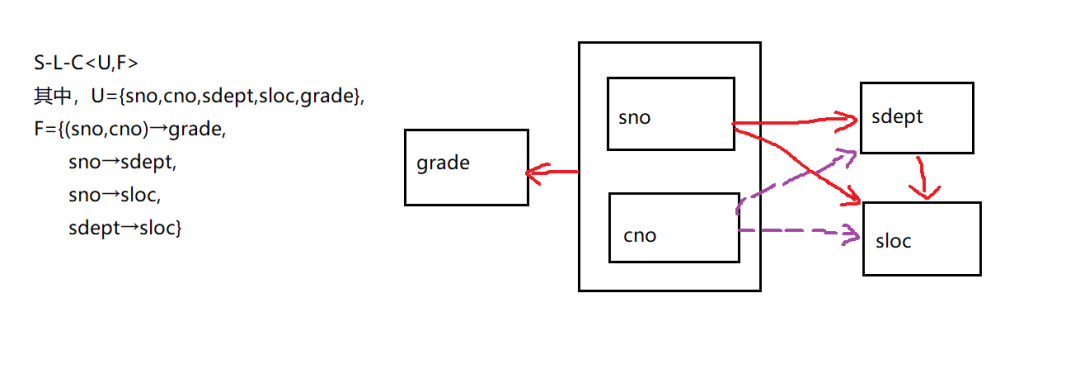
在函數(shù)依賴(lài)中還有以下幾種分類(lèi)：

1.1 平凡函數(shù)依賴(lài)和非平凡函數(shù)依賴(lài)

（1）X→Y 且 Y?X，則 X→Y 是非平凡函數(shù)依賴(lài)。例如 (sno,cno)→grade

（2）X→Y 且 Y∈X，則 X→Y 是平凡函數(shù)依賴(lài)。例如 (sno,cno)→sno， (sno,cno)→cno

在任意一關(guān)系模式下，平凡函數(shù)依賴(lài)必然成立，所以，在屬性之間的函數(shù)依賴(lài)關(guān)系一般討論非平凡函數(shù)依賴(lài)。

1.2 完全函數(shù)依賴(lài)和部分函數(shù)依賴(lài)

（1）X→Y，在 x 的真子集  X'，Y 均不依賴(lài)于 X'，則稱(chēng) Y 完全函數(shù)依賴(lài)于 X。在箭頭上面加上 F。

（2）X→Y，在 x 的真子集 X'，Y存在依賴(lài)于 X'，則稱(chēng)Y完全函數(shù)依賴(lài)于 X。在箭頭上面加上 P。

例如以下的例子，

1.3 傳遞函數(shù)依賴(lài)

X→Y，Y→Z 所以 X→Z，Z 傳遞函數(shù)依賴(lài)于 X。

例如，sno→sdept，sdept→sloc，所以 sno→sloc。

2. 碼

K 是關(guān)系 R<U,F> 中的屬性或者屬性集合（即 K 是 U 中的一個(gè)元素或者幾個(gè)元素的集合）

2.1 候選碼

若 U 完全函數(shù)依賴(lài)于K，則K稱(chēng)為R的一個(gè)候選碼（換言之，一個(gè)候選碼能推出所有屬性）。

例如（sno , cno）就是關(guān)系 S-L-C 的候選碼，因?yàn)?sno 和 cno 能推出 S-L-C 的所有元素

注意：一個(gè)關(guān)系中可能有多個(gè)候選碼

2.2 主碼和主屬性

主碼：在一個(gè)或者多個(gè)候選碼中選取其中一個(gè)作為主碼。

注意：在任意一個(gè)表中都有主碼，在建表中指定，如果沒(méi)有指定則所有屬性集合作為主碼

主屬性：包含在任何一個(gè)候選碼中的屬性（換言之，所有候選碼中的屬性的集合，因?yàn)橛锌赡艽嬖诙鄠€(gè)候選碼）

2.3 外碼

屬性 X 并非關(guān)系模式 R 的候選碼，但是 X 是另一個(gè)關(guān)系模式的候選碼。

3. 范式

范式是符合某一種級(jí)別的關(guān)系模式的集合。下圖就是表現(xiàn)范式級(jí)別（低范式包含高范式）。滿(mǎn)足高范式的同時(shí)，也一定滿(mǎn)足低范式。

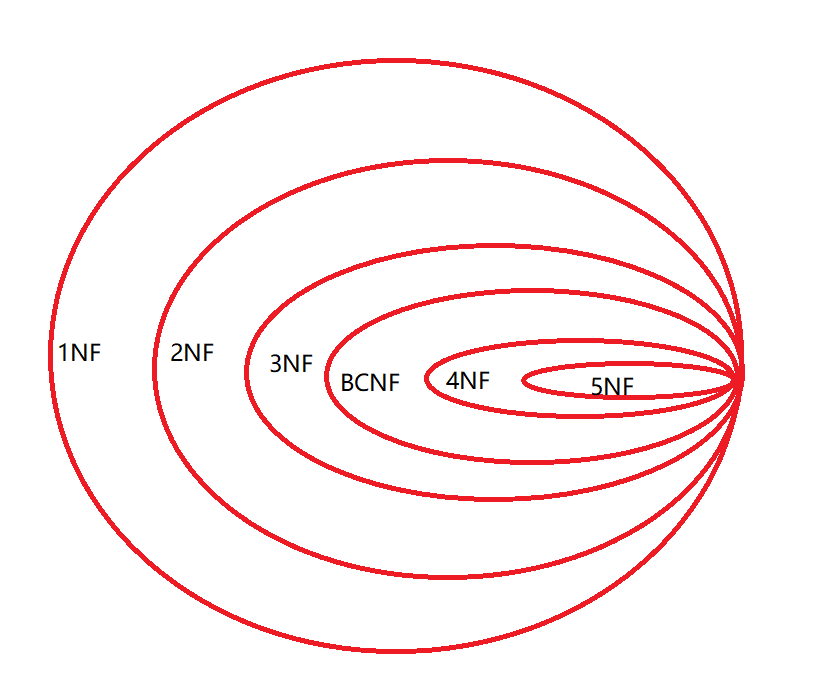
3.1 一范式——1NF

一關(guān)系模式 R 的所有屬性都是不可分的基本數(shù)據(jù)項(xiàng)（即表中不能再有表）。則 R∈1NF s。第一范式是對(duì)關(guān)系模式的最低要求，如果一個(gè)關(guān)系模式不滿(mǎn)足 1NF 則不能稱(chēng)為關(guān)系模式。

例如，以下這個(gè)關(guān)系就不滿(mǎn)足 1NF，因?yàn)椤俺煽?jī)”還能在分為“期中成績(jī)”和“期末成績(jī)”。

當(dāng)然，S-L-C 滿(mǎn)足 1NF，它中的元素都是不能再分。

3.2 二范式——2NF

若 R∈1NF，并且不存在非主屬性部分依賴(lài)于R的候選碼，則 R∈2NF。

這里還有很多的說(shuō)法，還可以說(shuō)每一個(gè)非主屬性都完全函數(shù)依賴(lài)于 R 的候選碼。

例如上述例子

sdept 和 sloc 部分函數(shù)依賴(lài)于 S-L-C 的候選碼 (sno,cno)，所以 S-L-C 不滿(mǎn)足 2NF。

則會(huì)出現(xiàn)問(wèn)題：

1. 插入異常：假設(shè)學(xué)號(hào) sno=123，專(zhuān)業(yè) sdept=IS，宿舍 sloc=N 的學(xué)生還沒(méi)有選課（則表示 cno 為空），則該學(xué)生無(wú)法將學(xué)生信息錄入進(jìn)系統(tǒng)。（因?yàn)?cno 為主屬性，不能為空）。
2. 刪除異常：假設(shè)一學(xué)生只選了一節(jié)課，但是現(xiàn)在他想將這門(mén)課退了，則將需要將這門(mén)課在這名學(xué)生系統(tǒng)中刪除，但是在刪除時(shí)，會(huì)把該學(xué)生的其它信息也會(huì)刪除（因?yàn)?cno 為主屬性）。
3. 數(shù)據(jù)冗余大：假設(shè)一學(xué)生選了10節(jié)課，則 sdept 和 sloc 也會(huì)重復(fù) 10 次。
4. 修改復(fù)雜：因?yàn)閿?shù)據(jù)冗余大，則修改也會(huì)復(fù)雜。

所以 S-L-C 不是一個(gè)很好的關(guān)系模式，所以我們需要將 S-L-C 分解，消除 sdept 和 sloc 對(duì)（sno,cno）的部分函數(shù)依賴(lài)。

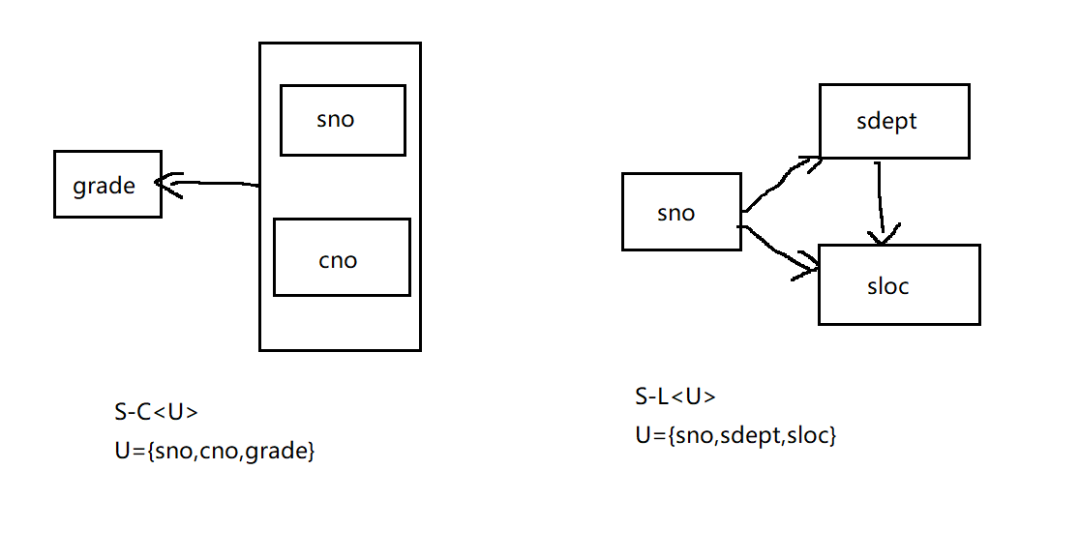
得到 S-C 和 S-L，其中 S-C 的候選碼為（sno , cno），非主屬性 grade 完全函數(shù)依賴(lài)于（sno , cno）所以 S-C∈2NF，同理非 S-L 的非主屬性 sdept 完全函數(shù)依賴(lài)于候選碼 sno，同理，sloc 完全函數(shù)依賴(lài)于候選碼 sno，所以 S-L∈2NF。

分解完畢，現(xiàn)在就解決上述的問(wèn)題了。

綜上，2NF 要注意非主屬性對(duì)候選碼的函數(shù)依賴(lài)，如果存在著部分函數(shù)依賴(lài)，則不滿(mǎn)足 2NF，反之，滿(mǎn)足 2NF。

3.3 三范式——3NF

簡(jiǎn)單的說(shuō)，在滿(mǎn)足 2NF 的基礎(chǔ)上，關(guān)系模式中不存在傳遞函數(shù)依賴(lài)。

例如在上述例子中的 S-L，存在 sno→sdept，sdept→sloc,并且有 sno→sloc，所以存在函數(shù)傳遞依賴(lài)，不滿(mǎn)足 3NF。

并且在 2NF 任然存在問(wèn)題，以上述 S-L為例：

1. 插入異常：若剛成立一個(gè)專(zhuān)業(yè)（sdept），但是還沒(méi)有學(xué)生（sno），則無(wú)法向數(shù)據(jù)庫(kù)中錄入sdept 和 sloc。

2. 刪除異常：若一個(gè)專(zhuān)業(yè)的學(xué)生全部畢業(yè)，需要將學(xué)號(hào)刪除時(shí)，則 sdept 和 sloc 也會(huì)被刪除。

3. 數(shù)據(jù)冗余大：若同一個(gè)專(zhuān)業(yè)的學(xué)生住在一起（即 sloc 都相同），就會(huì)有很多的 sloc 重復(fù)。

4. 修改復(fù)雜：因?yàn)閿?shù)據(jù)冗余大，所以要修改時(shí)很復(fù)雜。

所以 S-L 也不是一個(gè)很好的關(guān)系模式，需要將其分解，也就是讓 S-L 滿(mǎn)足3NF。

解決辦法：消除傳遞函數(shù)依賴(lài)。

這樣就解決了 2NF 存在的問(wèn)題了。

這里補(bǔ)充一個(gè)知識(shí)點(diǎn)：

1. 所有高范式成立，則低范式也一定成立，即若 R∈3NF，則一定 R∈2NF。
2. 若 R∈3NF，則 R 的每一個(gè)非主屬性既不部分函數(shù)依賴(lài)于候選碼，也不傳遞函數(shù)依賴(lài)于候選碼。

3.4 BCNF

沒(méi)有任何屬性（主屬性和非主屬性）對(duì)候選碼的部分函數(shù)依賴(lài)和傳遞函數(shù)依賴(lài)。

以下例子，

因?yàn)楹蜻x碼為（S,T）和（S,J），所以主屬性為（S,T,J），不存在非主屬性。所以一定滿(mǎn)足3NF。

但是這里存在 主屬性對(duì)候選碼的部分函數(shù)依賴(lài)，所以不滿(mǎn)足 BCNF。

3.5 4NF 和 5NF

當(dāng)然還有 4NF 和 5NF，原理和以上的一樣，不是很重要。

這里就簡(jiǎn)單的了解一下，

4NF：當(dāng) R∈BCNF，消除非平凡且非函數(shù)依賴(lài)的多值依賴(lài)。

5NF：當(dāng) R∈4NF，消除不是由候選碼所蘊(yùn)含的連接依賴(lài)。如果關(guān)系模式R中的每一個(gè)連接依賴(lài)均由 R 的候選碼所隱含。

總結(jié)

在范式的學(xué)習(xí)中，一定要把知識(shí)點(diǎn)弄清，例如部分函數(shù)依賴(lài)，完全函數(shù)依賴(lài)，候選碼，主屬性等等。把原理搞懂了，很有利于后面的學(xué)習(xí)。其實(shí)搞懂了范式還是非常簡(jiǎn)單的。