【機(jī)器學(xué)習(xí)基礎(chǔ)】通俗易懂無監(jiān)督學(xué)習(xí)K-Means聚類算法及代碼實(shí)踐
K-Means是一種無監(jiān)督學(xué)習(xí)方法,用于將無標(biāo)簽的數(shù)據(jù)集進(jìn)行聚類。其中K指集群的數(shù)量,Means表示尋找集群中心點(diǎn)的手段。
一、 無監(jiān)督學(xué)習(xí) K-Means
貼標(biāo)簽是需要花錢的。
所以人們研究處理無標(biāo)簽數(shù)據(jù)集的方法。(筆者狹隘了)
面對無標(biāo)簽的數(shù)據(jù)集,我們期望從數(shù)據(jù)中找出一定的規(guī)律。一種最簡單也最快速的聚類算法應(yīng)運(yùn)而生---K-Means。
它的核心思想很簡單:物以類聚。
用直白的話簡單解釋它的算法執(zhí)行過程如下:
隨便選擇K個(gè)中心點(diǎn)(大哥)。 把距離它足夠近的數(shù)據(jù)(小弟)吸納為成員,聚成K個(gè)集群(組織)。 各集群(組織)內(nèi)部重新選擇中心點(diǎn)(大哥),選擇標(biāo)準(zhǔn)是按照距離取均值作為中心點(diǎn)(大哥)。 重復(fù)2、3步驟直到收斂(組織成員相對穩(wěn)定)。
這就是黑澀會形成聚類的過程。
二、 K-Means代碼實(shí)踐
2.1 鳶尾花數(shù)據(jù)集
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# 大家不用在意這個(gè)域名
df = pd.read_csv('https://blog.caiyongji.com/assets/iris.csv')
sns.scatterplot(x='petal_length',y='petal_width',data=df,hue='species')
我們得到帶標(biāo)簽的數(shù)據(jù)如下:
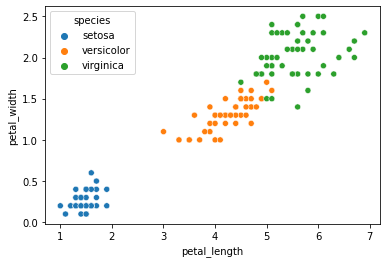
2.2 K-Means訓(xùn)練數(shù)據(jù)
我們移除數(shù)據(jù)標(biāo)簽,僅使用花瓣長、寬作為數(shù)據(jù)輸入,并使用無監(jiān)督學(xué)習(xí)方法K-Means進(jìn)行訓(xùn)練。
X = df[['petal_length','petal_width']].to_numpy()
from sklearn.cluster import KMeans
k = 2
kmeans = KMeans(n_clusters=k, random_state=42)
y_pred = kmeans.fit_predict(X)
plt.plot(X[y_pred==1, 0], X[y_pred==1, 1], "ro", label="group 1")
plt.plot(X[y_pred==0, 0], X[y_pred==0, 1], "bo", label="group 0")
# plt.legend(loc=2)
plt.show()
得到分類數(shù)據(jù)如下,我們并不知道下方數(shù)據(jù)類別分別代表什么意義。
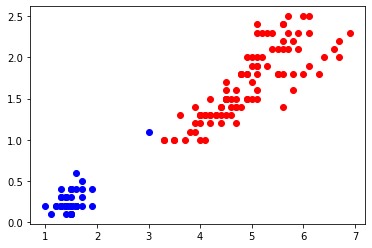
我們將K分別取1-6的值,可得到如下圖所示分類結(jié)果:
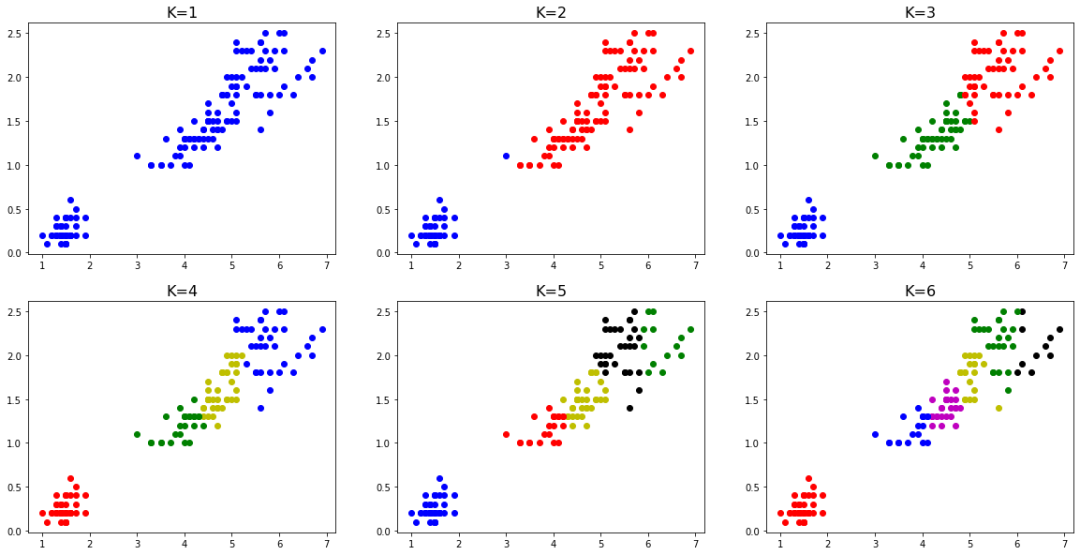
那么K值的選擇有什么意義呢?我們?nèi)绾芜x擇?
三、K的選擇
3.1 慣性指標(biāo)(inertia)
K-Means的慣性計(jì)算方式是,每個(gè)樣本與最接近的集群中心點(diǎn)的均方距離的總和。
kmeans_per_k = [KMeans(n_clusters=k, random_state=42).fit(X)
for k in range(1, 10)]
inertias = [model.inertia_ for model in kmeans_per_k]
plt.figure(figsize=(8, 3.5))
plt.plot(range(1, 10), inertias, "bo-")
plt.xlabel("$k$", fontsize=14)
plt.ylabel("Inertia", fontsize=14)
plt.annotate('Elbow',
xy=(2, inertias[2]),
xytext=(0.55, 0.55),
textcoords='figure fraction',
fontsize=16,
arrowprops=dict(facecolor='black', shrink=0.1)
)
plt.axis([1, 8.5, 0, 1300])
plt.show()
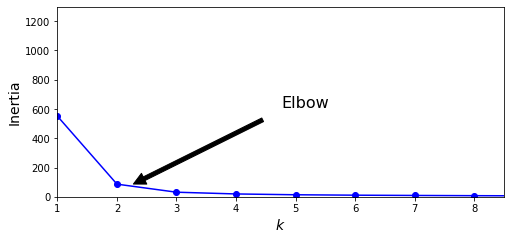
以上代碼中model.inertia_即K-Means方法中的慣性指標(biāo)。
一般地,慣性越小模型越好,但伴隨K值的增大,慣性下降的速度變的很慢,因此我們選擇“肘部”的K值,作為最優(yōu)的K值選擇。
3.2 輪廓系數(shù)指標(biāo)(silhouette)
K-Means的輪廓系數(shù)計(jì)算方式是,與集群內(nèi)其他樣本的平均距離記為a,與外部集群樣本的平均距離記為b,輪廓系數(shù)(b-a)/max(a,b)。
from sklearn.metrics import silhouette_score
silhouette_scores = [silhouette_score(X, model.labels_)
for model in kmeans_per_k[1:]]
plt.figure(figsize=(8, 3))
plt.plot(range(2, 10), silhouette_scores, "bo-")
plt.xlabel("$k$", fontsize=14)
plt.ylabel("Silhouette score", fontsize=14)
plt.axis([1.8, 8.5, 0.55, 0.8])
plt.show()
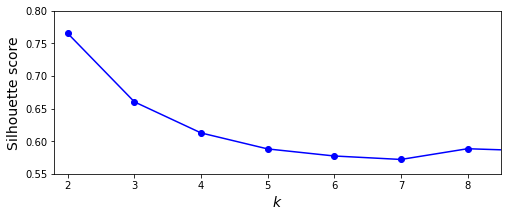
以上代碼中silhouette_score方法可取得K-Means的輪廓系數(shù)值。
一般地,輪廓系數(shù)指標(biāo)越大越好,我們可以看到當(dāng)K為2、3時(shí)均可取得不錯(cuò)的聚類效果。
四、自動(dòng)選擇K值(拓展)
4.1 簡單理解貝葉斯定理
白話解釋貝葉斯:當(dāng)有新的證據(jù)出現(xiàn)時(shí),不確定的事情更加確信了。 這里的“確信”是指對不確定的事情的信心程度。
公式(可忽略):
其中,P(A) 表示事件A發(fā)生的概率,P(A|B)表示事件B發(fā)生時(shí)事件A發(fā)生的概率。上面的公式中B就是所謂的證據(jù)。這里要注意的是,P(B)的出現(xiàn)讓P(A|B)變的更確定了,并不是說概率變高了或者變低了。概率的高或者低都是一種確定。它是一種信心程度的體現(xiàn)。
4.2 貝葉斯高斯混合模型
我們使用BayesianGaussianMixture方法,而無需指定明確的K值。
from sklearn.mixture import BayesianGaussianMixture
bgm = BayesianGaussianMixture(n_components=10, n_init=10, random_state=42)
y_pred = bgm.fit_predict(X)
np.round(bgm.weights_, 2)
輸出: array([0.4 , 0.33, 0.27, 0. , 0. , 0. , 0. , 0. , 0. , 0. ])
以上代碼的執(zhí)行邏輯是,初始化10個(gè)集群,不斷調(diào)整有關(guān)集群數(shù)貝葉斯先驗(yàn)知識,來將不必要的集群權(quán)重設(shè)為0(或接近0),來確定最終K值。
五、總結(jié)(系列完結(jié))
5.1 機(jī)器學(xué)習(xí)系列完結(jié)
我相信,截至到目前,大家對機(jī)器學(xué)習(xí)已經(jīng)有了一個(gè)基本的認(rèn)識。最重要的是,大家親手實(shí)踐了機(jī)器學(xué)習(xí)的代碼。無論你對機(jī)器學(xué)習(xí)有多么模糊的認(rèn)識,都能近距離的接觸到機(jī)器學(xué)習(xí),這一點(diǎn)很重要。
當(dāng)初,我發(fā)現(xiàn)市面上大部分的教程都對數(shù)學(xué)有強(qiáng)依賴,讓很多人敬而遠(yuǎn)之。我覺得,無論頂尖的科學(xué)研究還是普羅大眾的教育科普都有其不可替代的巨大價(jià)值。流于表面的廣泛未必沒有其意義,因此我選擇了舍棄嚴(yán)謹(jǐn),貼近通俗。
當(dāng)然,想要深耕于AI領(lǐng)域,數(shù)學(xué)是充分且必要的條件。如果付得起時(shí)間和機(jī)會成本,請認(rèn)真且努力,絕不會辜負(fù)你。
5.2 深度學(xué)習(xí)系列開始
深度學(xué)習(xí)是一臺結(jié)構(gòu)復(fù)雜的機(jī)器,但它的操作卻相對簡單。甚至,會給你比傳統(tǒng)機(jī)器學(xué)習(xí)算法更簡單的感受。
我們拭目以待!感謝大家!
往期文章:
機(jī)器學(xué)習(xí)(五):通俗易懂決策樹與隨機(jī)森林及代碼實(shí)踐 機(jī)器學(xué)習(xí)(四):通俗理解支持向量機(jī)SVM及代碼實(shí)踐 機(jī)器學(xué)習(xí)(三):理解邏輯回歸及二分類、多分類代碼實(shí)踐 機(jī)器學(xué)習(xí)(二):理解線性回歸與梯度下降并做簡單預(yù)測 機(jī)器學(xué)習(xí)(一):5分鐘理解機(jī)器學(xué)習(xí)并上手實(shí)踐 前置機(jī)器學(xué)習(xí)(五):30分鐘掌握常用Matplotlib用法 前置機(jī)器學(xué)習(xí)(四):一文掌握Pandas用法 前置機(jī)器學(xué)習(xí)(三):30分鐘掌握常用NumPy用法 前置機(jī)器學(xué)習(xí)(二):30分鐘掌握常用Jupyter Notebook用法 前置機(jī)器學(xué)習(xí)(一):數(shù)學(xué)符號及希臘字母
往期精彩回顧
本站qq群851320808,加入微信群請掃碼:
