機(jī)器學(xué)習(xí) | KMeans聚類分析詳解
大家好,我是老表,今天給大家分享一篇機(jī)器學(xué)習(xí)KMaens聚類分析算法文章,在后面的實(shí)戰(zhàn)中我們將用到該算法,希望大家認(rèn)真學(xué)習(xí)閱讀,覺(jué)得對(duì)自己學(xué)習(xí)有幫助的話,歡迎點(diǎn)贊、轉(zhuǎn)發(fā)、留言。
大量數(shù)據(jù)中具有"相似"特征的數(shù)據(jù)點(diǎn)或樣本劃分為一個(gè)類別。聚類分析提供了樣本集在非監(jiān)督模式下的類別劃分。聚類的基本思想是"物以類聚、人以群分",將大量數(shù)據(jù)集中相似的數(shù)據(jù)樣本區(qū)分出來(lái),并發(fā)現(xiàn)不同類的特征。
聚類模型可以建立在無(wú)類標(biāo)記的數(shù)據(jù)上,是一種非監(jiān)督的學(xué)習(xí)算法。盡管全球每日新增數(shù)據(jù)量以PB或EB級(jí)別增長(zhǎng),但是大部分?jǐn)?shù)據(jù)屬于無(wú)標(biāo)注甚至非結(jié)構(gòu)化。所以相對(duì)于監(jiān)督學(xué)習(xí),不需要標(biāo)注的無(wú)監(jiān)督學(xué)習(xí)蘊(yùn)含了巨大的潛力與價(jià)值。聚類根據(jù)數(shù)據(jù)自身的距離或相似度將他們劃分為若干組,劃分原則是組內(nèi)樣本最小化而組間距離最大化。
聚類分析常用于數(shù)據(jù)探索或挖掘前期
沒(méi)有先驗(yàn)經(jīng)驗(yàn)做探索性分析 樣本量較大時(shí)做預(yù)處理 常用于解決
數(shù)據(jù)集可以分幾類;每個(gè)類別有多少樣本量 不同類別中各個(gè)變量的強(qiáng)弱關(guān)系如何 不同類型的典型特征是什么 一般應(yīng)用場(chǎng)景
群類別間的差異性特征分析 群類別內(nèi)的關(guān)鍵特征提取 圖像壓縮、分割、圖像理解 異常檢測(cè) 數(shù)據(jù)離散化 當(dāng)然聚類分析也有其缺點(diǎn)
無(wú)法提供明確的行動(dòng)指向 數(shù)據(jù)異常對(duì)結(jié)果有影響
本文將從算法原理、優(yōu)化目標(biāo)、sklearn聚類算法、算法優(yōu)缺點(diǎn)、算法優(yōu)化、算法重要參數(shù)、衡量指標(biāo)以及案例等方面詳細(xì)介紹KMeans算法。
KMeans
K均值(KMeans)是聚類中最常用的方法之一,基于點(diǎn)與點(diǎn)之間的距離的相似度來(lái)計(jì)算最佳類別歸屬。
KMeans算法通過(guò)試著將樣本分離到 個(gè)方差相等的組中來(lái)對(duì)數(shù)據(jù)進(jìn)行聚類,從而最小化目標(biāo)函數(shù) (見(jiàn)下文)。該算法要求指定集群的數(shù)量。它可以很好地?cái)U(kuò)展到大量的樣本,并且已經(jīng)在許多不同領(lǐng)域的廣泛應(yīng)用領(lǐng)域中使用。
被分在同一個(gè)簇中的數(shù)據(jù)是有相似性的,而不同簇中的數(shù)據(jù)是不同的,當(dāng)聚類完畢之后,我們就要分別去研究每個(gè)簇中的樣本都有什么樣的性質(zhì),從而根據(jù)業(yè)務(wù)需求制定不同的商業(yè)或者科技策略。常用于客戶分群、用戶畫像、精確營(yíng)銷、基于聚類的推薦系統(tǒng)。
算法原理
從 個(gè)樣本數(shù)據(jù)中隨機(jī)選取 個(gè)質(zhì)心作為初始的聚類中心。質(zhì)心記為
定義優(yōu)化目標(biāo)
開(kāi)始循環(huán),計(jì)算每個(gè)樣本點(diǎn)到那個(gè)質(zhì)心到距離,樣本離哪個(gè)近就將該樣本分配到哪個(gè)質(zhì)心,得到K個(gè)簇
對(duì)于每個(gè)簇,計(jì)算所有被分到該簇的樣本點(diǎn)的平均距離作為新的質(zhì)心
直到 收斂,即所有簇不再發(fā)生變化。
優(yōu)化目標(biāo)
KMeans 在進(jìn)行類別劃分過(guò)程及最終結(jié)果,始終追求"簇內(nèi)差異小,簇間差異大",其中差異由樣本點(diǎn)到其所在簇的質(zhì)心的距離衡量。在KNN算法學(xué)習(xí)中,我們學(xué)習(xí)到多種常見(jiàn)的距離 ---- 歐幾里得距離、曼哈頓距離、余弦距離。
在sklearn中的KMeans使用歐幾里得距離:
(cluster Sum of Square), 又叫做Inertia。而將一個(gè)數(shù)據(jù)集中的所有簇的簇內(nèi)平方和相加,就得到了整體平方和(Total Cluster Sum of Square),又叫做Total Inertia。Total Inertia越小,代表著每個(gè)簇內(nèi)樣本越相似,聚類的效果就越好。因此 KMeans 追求的是,求解能夠讓Inertia最小化的質(zhì)心。
KMeans有損失函數(shù)嗎?損失函數(shù)本質(zhì)是用來(lái)衡量模型的擬合效果的,只有有著求解參數(shù)需求的算法,才會(huì)有損失函數(shù)。
KMeans不求解什么參數(shù),它的模型本質(zhì)也沒(méi)有在擬合數(shù)據(jù),而是在對(duì)數(shù)據(jù)進(jìn)行一 種探索。另外,在決策樹(shù)中有衡量分類效果的指標(biāo)準(zhǔn)確度
accuracy,準(zhǔn)確度所對(duì)應(yīng)的損失叫做泛化誤差,但不能通過(guò)最小化泛化誤差來(lái)求解某個(gè)模型中需要的信息,我們只是希望模型的效果上表現(xiàn)出來(lái)的泛化誤差很小。因此決策樹(shù),KNN等算法,是絕對(duì)沒(méi)有損失函數(shù)的。
雖然在sklearn中只能被動(dòng)選用歐式距離,但其他距離度量方式同樣可以用來(lái)衡量簇內(nèi)外差異。不同距離所對(duì)應(yīng)的質(zhì)心選擇方法和Inertia如下表所示, 在KMeans中,只要使用了正確的質(zhì)心和距離組合,無(wú)論使用什么樣的距離,都可以達(dá)到不錯(cuò)的聚類效果。
| 距離度量 | 質(zhì)心 | Inertia |
|---|---|---|
| 歐幾里得距離 | 均值 | 最小化每個(gè)樣本點(diǎn)到質(zhì)心的歐式距離之和 |
| 曼哈頓距離 | 中位數(shù) | 最小化每個(gè)樣本點(diǎn)到質(zhì)心的曼哈頓距離之和 |
| 余弦距離 | 均值 | 最小化每個(gè)樣本點(diǎn)到質(zhì)心的余弦距離之和 |
sklearn.cluster.KMeans
語(yǔ)法:
sklearn.cluster.KMeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='auto', verbose=0, random_state=None, copy_x=True, n_jobs=None, algorithm='auto')
參數(shù)與接口詳解見(jiàn)文末附錄
例:
>>> from sklearn.cluster import KMeans
>>> import numpy as np
>>> X = np.array([[1, 2], [1, 4], [1, 0],
... [10, 2], [10, 4], [10, 0]])
>>> kmeans = KMeans(n_clusters=2, random_state=0).fit(X)
>>> kmeans.labels_
array([1, 1, 1, 0, 0, 0], dtype=int32)
>>> kmeans.predict([[0, 0], [12, 3]])
array([1, 0], dtype=int32)
>>> kmeans.cluster_centers_
array([[10., 2.],
[ 1., 2.]])
KMeans算法優(yōu)缺點(diǎn)
優(yōu)點(diǎn)
KMeans算法是解決聚類問(wèn)題的一種經(jīng)典算法, 算法簡(jiǎn)單、快速 。 算法嘗試找出使平方誤差函數(shù)值最小的 個(gè)劃分。當(dāng)簇是密集的、球狀或團(tuán)狀的,且簇與簇之間區(qū)別明顯時(shí),聚類效果較好 。
缺點(diǎn)
KMeans方法只有在簇的平均值被定義的情況下才能使用,且對(duì)有些分類屬性的數(shù)據(jù)不適合。 要求用戶必須事先給出要生成的簇的數(shù)目 。 對(duì)初值敏感,對(duì)于不同的初始值,可能會(huì)導(dǎo)致不同的聚類結(jié)果。 不適合于發(fā)現(xiàn)非凸面形狀的簇,或者大小差別很大的簇。 KMeans本質(zhì)上是一種基于歐式距離度量的數(shù)據(jù)劃分方法,均值和方差大的維度將對(duì)數(shù)據(jù)的聚類結(jié)果產(chǎn)生決定性影響。所以在聚類前對(duì)數(shù)據(jù)(具體的說(shuō)是每一個(gè)維度的特征)做歸一化(點(diǎn)擊查看歸一化詳解)和單位統(tǒng)一至關(guān)重要。此外,異常值會(huì)對(duì)均值計(jì)算產(chǎn)生較大影響,導(dǎo)致中心偏移,因此對(duì)于"噪聲"和孤立點(diǎn)數(shù)據(jù)最好能提前過(guò)濾 。
KMeans算法優(yōu)化
KMeans算法雖然效果不錯(cuò),但是每一次迭代都需要遍歷全量的數(shù)據(jù),一旦數(shù)據(jù)量過(guò)大,由于計(jì)算復(fù)雜度過(guò)大迭代的次數(shù)過(guò)多,會(huì)導(dǎo)致收斂速度非常慢。
由KMeans算法原來(lái)可知,KMeans在聚類之前首先需要初始化 個(gè)簇中心,因此 KMeans算法對(duì)初值敏感,對(duì)于不同的初始值,可能會(huì)導(dǎo)致不同的聚類結(jié)果。因初始化是個(gè)"隨機(jī)"過(guò)程,很有可能 個(gè)簇中心都在同一個(gè)簇中,這種情況 KMeans 聚類算法很大程度上都不會(huì)收斂到全局最小。
想要優(yōu)化KMeans算法的效率問(wèn)題,可以從以下兩個(gè)思路優(yōu)化算法,一個(gè)是樣本數(shù)量太大,另一個(gè)是迭代次數(shù)過(guò)多。
MiniBatchKMeans 聚類算法
mini batch 優(yōu)化思想非常樸素,既然全體樣本當(dāng)中數(shù)據(jù)量太大,會(huì)使得我們迭代的時(shí)間過(guò)長(zhǎng),那么隨機(jī)從整體當(dāng)中做一個(gè)抽樣,選取出一小部分?jǐn)?shù)據(jù)來(lái)代替整體以達(dá)到縮小數(shù)據(jù)規(guī)模的目的。
mini batch 優(yōu)化非常重要,不僅重要而且在機(jī)器學(xué)習(xí)領(lǐng)域廣為使用。在大數(shù)據(jù)的場(chǎng)景下,幾乎所有模型都需要做mini batch優(yōu)化,而MiniBatchKMeans就是mini batch 優(yōu)化的一個(gè)應(yīng)用。直接上模型比較MiniBatchKMeans和KMeans兩種算法計(jì)算速度(樣本量1,000,000)
KMeans用時(shí)接近 6 秒鐘,而MiniBatchKMeans僅用時(shí)不到 1 秒鐘
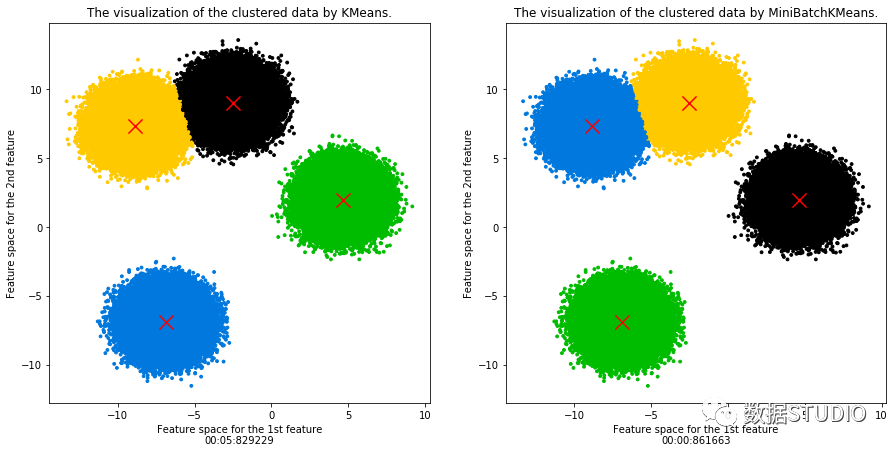
且聚類中心基本一致
>>> KMeans.cluster_centers_
array([[-2.50889102, 9.01143598],
[-6.88150415, -6.88090477],
[ 4.63628843, 1.97271152],
[-8.83895916, 7.32493568]])
>>> MiniBatchKMeans.cluster_centers_
array([[-2.50141353, 8.97807161],
[-6.88418974, -6.87048909],
[ 4.65410395, 1.99254911],
[-8.84903186, 7.33075289]])mini batch優(yōu)化方法是通過(guò)減少計(jì)算樣本量來(lái)達(dá)到縮短迭代時(shí)長(zhǎng),另一種方法是降低收斂需要的迭代次數(shù),從而達(dá)到快速收斂的目的。收斂的速度除了取決于每次迭代的變化率之外,另一個(gè)重要指標(biāo)就是迭代起始的位置。2007年Arthur, David, and Sergei Vassilvitskii三人發(fā)表了論文"k-means++: The advantages of careful seeding" http://ilpubs.stanford.edu:8090/778/1/2006-13.pdf,他們開(kāi)發(fā)了'k-means++'初始化方案,使得初始質(zhì)心(通常)彼此遠(yuǎn)離,以此來(lái)引導(dǎo)出比隨機(jī)初始化更可靠的結(jié)果。
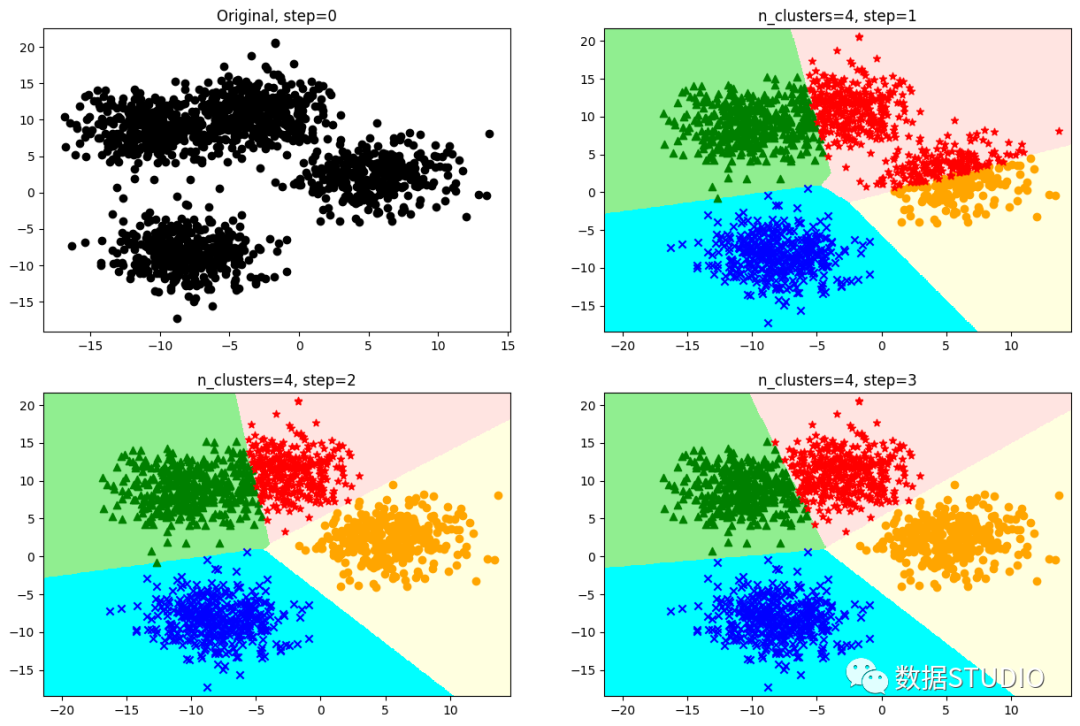
'k-means++' 聚類算法
'k-means++'聚類算法是在KMeans算法基礎(chǔ)上,針對(duì)迭代次數(shù),優(yōu)化選擇初始質(zhì)心的方法。sklearn.cluster.KMeans 中默認(rèn)參數(shù)為 init='k-means++',其算法原理為在初始化簇中心時(shí),逐個(gè)選取 個(gè)簇中心,且離其他簇中心越遠(yuǎn)的樣本越有可能被選為下個(gè)簇中心。
算法步驟:
從數(shù)據(jù)即 中隨機(jī)(均勻分布)選取一個(gè)樣本點(diǎn)作為第一個(gè)初始聚類中心
計(jì)算每個(gè)樣本與當(dāng)前已有聚類中心之間的最短距離;再計(jì)算每個(gè)樣本點(diǎn)被選為下個(gè)聚類中心的概率,最后選擇最大概率值所對(duì)應(yīng)的樣本點(diǎn)作為下一個(gè)簇中心
重復(fù)上步驟,直到選擇個(gè)聚類中心
'k-means++'算法初始化的簇中心彼此相距都十分的遠(yuǎn),從而不可能再發(fā)生初始簇中心在同一個(gè)簇中的情況。當(dāng)然'k-means++'本身也具有隨機(jī)性,并不一定每一次隨機(jī)得到的起始點(diǎn)都能有這么好的效果,但是通過(guò)策略,我們可以保證即使出現(xiàn)最壞的情況也不會(huì)太壞。
'k-means++' code:
def InitialCentroid(x, K):
c1_idx = int(np.random.uniform(0, len(x))) # Draw samples from a uniform distribution.
centroid = x[c1_idx].reshape(1, -1) # choice the first center for cluster.
k = 1
n = x.shape[0] # number of samples
while k < K:
d2 = []
for i in range(n):
subs = centroid - x[i, :] # D(x) = (x_1, y_1) - (x, y)
dimension2 = np.power(subs, 2) # D(x)^2
dimension_s = np.sum(dimension2, axis=1) # sum of each row
d2.append(np.min(dimension_s))
new_c_idx = np.argmax(d2)
centroid = np.vstack([centroid, x[new_c_idx]])
k += 1
return centroid
重要參數(shù)
初始質(zhì)心
KMeans算法的第一步"隨機(jī)"在樣本中抽取 個(gè)樣本作為初始質(zhì)心,因此并不符合"穩(wěn)定且更快"的需求。因此可通過(guò)random_state參數(shù)來(lái)指定隨機(jī)數(shù)種子,以控制每次生成的初始質(zhì)心都在相同位置。
一個(gè)random_state對(duì)應(yīng)一個(gè)質(zhì)心隨機(jī)初始化的隨機(jī)數(shù)種子。如果不指定隨機(jī)數(shù)種子,則 sklearn中的KMeans并不會(huì)只選擇一個(gè)隨機(jī)模式扔出結(jié)果,而會(huì)在每個(gè)隨機(jī)數(shù)種子下運(yùn)行多次,并使用結(jié)果最好的一個(gè)隨機(jī)數(shù)種子來(lái)作為初始質(zhì)心。我們可以使用參數(shù)n_init來(lái)選擇,每個(gè)隨機(jī)數(shù)種子下運(yùn)行的次數(shù)。
而以上兩種方法仍然避免不了基于隨機(jī)性選取 個(gè)質(zhì)心的本質(zhì)。在sklearn中,我們使用參數(shù)init ='k-means++'來(lái)選擇使用'k-means++'作為質(zhì)心初始化的方案。
init : 可輸入
"k-means++","random"或者一個(gè)n維數(shù)組。這是初始化質(zhì)心的方法,默認(rèn)"k-means++"。輸入"k- means++":一種為K均值聚類選擇初始聚類中心的聰明的辦法,以加速收斂。如果輸入了n維數(shù)組,數(shù)組的形狀應(yīng)該是(n_clusters,n_features)并給出初始質(zhì)心。random_state : 控制每次質(zhì)心隨機(jī)初始化的隨機(jī)數(shù)種子。
n_init : 整數(shù),默認(rèn)10,使用不同的質(zhì)心隨機(jī)初始化的種子來(lái)運(yùn)行
KMeans算法的次數(shù)。最終結(jié)果會(huì)是基于Inertia來(lái)計(jì)算的n_init次連續(xù)運(yùn)行后的最佳輸出。
迭代停止
max_iter : 整數(shù),默認(rèn)300,單次運(yùn)行的
KMeans算法的最大迭代次數(shù)。tol : 浮點(diǎn)數(shù),默認(rèn)
1e-4,兩次迭代間Inertia下降的量,如果兩次迭代之間Inertia下降的值小于tol所設(shè)定的值,迭代就會(huì)停下。
衡量指標(biāo)
聚類模型的結(jié)果不是某種標(biāo)簽輸出,并且聚類的結(jié)果是不確定的,其優(yōu)劣由業(yè)務(wù)需求或者算法需求來(lái)決定,并且沒(méi)有永遠(yuǎn)的正確答案。那么如何衡量聚類的效果呢?
衡量簇內(nèi)差異來(lái)衡量聚類的效果
簇內(nèi)平方和:
Total_Inertia肘部法(手肘法)認(rèn)為圖上的拐點(diǎn)就是 的最佳值。
# 應(yīng)用肘部法則確定 kmeans方法中的k
from scipy.spatial.distance import cdist # 計(jì)算兩個(gè)輸入集合的每對(duì)之間的距離。
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.datasets import make_blobs
plt.style.use('seaborn')
plt.rcParams['font.sans-serif']=['Simhei'] #顯示中文
plt.rcParams['axes.unicode_minus']=False #顯示負(fù)號(hào)
X, y = make_blobs(n_samples=5000, centers=4, cluster_std = 2.5, n_features=2,random_state=42)
K=range(1,10)
# 直接計(jì)算sse
sse_result=[]
for k in K:
kmeans=KMeans(n_clusters=k, random_state=666)
kmeans.fit(X)
sse_result.append(sum(np.min(cdist(X,kmeans.cluster_centers_,'euclidean'),axis=1))/X.shape[0])
plt.figure(figsize=(16,5))
plt.subplot(1,2,1)
plt.plot(K,sse_result,'gp-')
plt.xlabel('k',fontsize=20)
plt.ylabel(u'平均畸變程度')
plt.title(u'肘部法則確定最佳的K值(1)',fontdict={'fontsize':15})
# 第二種,使用inertia_
L = []
for k in K:
kmeans = KMeans(n_clusters=k, random_state=666)
kmeans.fit(X)
L.append((k, kmeans.inertia_))
a = pd.DataFrame(L)
a.columns = ['k', 'inertia']
plt.subplot(1,2,2)
plt.plot(a.k, a.inertia,'gp-')
plt.xlabel('k',fontsize=20)
plt.ylabel('inertia')
plt.title(u'肘部法則確定最佳的K值(2)',fontdict={'fontsize':15})
plt.xticks(a.k)
plt.show();
輸出結(jié)果:

但其有很大的局限:
它的計(jì)算太容易受到特征數(shù)目的影響。 它不是有界的, Inertia是越小越好,但并不知道合適達(dá)到模型的極限,能否繼續(xù)提高。它會(huì)受到超參數(shù) 的影響,隨著 越大, Inertia注定會(huì)越來(lái)越小,但并不代表模型效果越來(lái)越好。Inertia對(duì)數(shù)據(jù)的分布有假設(shè),它假設(shè)數(shù)據(jù)滿足凸分布,并且它假設(shè)數(shù)據(jù)是各向同性的(isotropic),所以使用Inertia作為評(píng)估指標(biāo),會(huì)讓聚類算法在一些細(xì)長(zhǎng)簇,環(huán)形簇,或者不規(guī)則形狀的流形時(shí)表現(xiàn)不佳。
其他衡量指標(biāo)
1、真實(shí)標(biāo)簽已知時(shí)
可以用聚類算法的結(jié)果和真實(shí)結(jié)果來(lái)衡量聚類的效果。但需要用到聚類分析的場(chǎng)景,大部分均屬于無(wú)真實(shí)標(biāo)簽的情況,因此以下模型評(píng)估指標(biāo)了解即可。
| 模型評(píng)估指標(biāo) | 說(shuō)明 |
|---|---|
| 互信息分 普通互信息分 metrics.adjusted_mutual_info_score (y_pred, y_true)調(diào)整的互信息分 metrics.mutual_info_score (y_pred, y_true)標(biāo)準(zhǔn)化互信息分 metrics.normalized_mutual_info_score (y_pred, y_true) | 取值范圍在(0,1)之中越接近1, 聚類效果越好在隨機(jī)均勻聚類下產(chǎn)生0分。 |
| V-measure:基于條件上分析的一系列直觀度量 同質(zhì)性:是否每個(gè)簇僅包含單個(gè)類的樣本 metrics.homogeneity_score(y_true, y_pred)完整性:是否給定類的所有樣本都被分配給同一個(gè)簇中 同質(zhì)性和完整性的調(diào)和平均,叫做V-measure metrics.v_measure_score(labels_true, labels_pred)三者可以被一次性計(jì)算出來(lái): metrics.homogeneity_completeness_v_measure(labels_true, labels_pred) | 取值范圍在(0,1)之中越接近1, 聚類效果越好由于分為同質(zhì)性和完整性兩種度量,可以更仔細(xì)地研究,模型到底哪個(gè)任務(wù)做得不夠好。對(duì)樣本分布沒(méi)有假設(shè),在任何分布上都可以有不錯(cuò)的表現(xiàn)在隨機(jī)均勻聚類下不會(huì)產(chǎn)生0分。 |
調(diào)整蘭德系數(shù)metrics.adjusted_rand_score(y_true, y_pred) | 取值在(-1,1)之間,負(fù)值象征著簇內(nèi)的點(diǎn)差異巨大,甚至相互獨(dú)立,正類的 蘭德系數(shù)比較優(yōu)秀, 越接近1越好對(duì)樣本分布沒(méi)有假設(shè),在任何分布上都可以有不錯(cuò)的表現(xiàn),尤其是在具有"折疊"形狀的數(shù)據(jù)上表現(xiàn)優(yōu)秀,在隨機(jī)均勻聚類下產(chǎn)生0分。 |
輪廓系數(shù)
對(duì)沒(méi)有真實(shí)標(biāo)簽的數(shù)據(jù)進(jìn)行探索,常用輪廓系數(shù)評(píng)價(jià)聚類算法模型效果。
樣本與其自身所在的簇中的其他樣本的相似度
a,等于樣本與同一簇中所有其他點(diǎn)之間的平均距離 。樣本與其他簇中的樣本的相似度
b,等于樣本與下一個(gè)最近的簇中的所有點(diǎn)之間的平均距離。
b永遠(yuǎn)大于a,并且大得越多越好。單個(gè)樣本的輪廓系數(shù)計(jì)算為:越接近 1 表示樣本與自己所在的簇中的樣本很相似,并且與其他簇中的樣本不相似,當(dāng)樣本點(diǎn)與簇外的樣本更相似的時(shí)候,輪廓系數(shù)就為負(fù)。
當(dāng)輪廓系數(shù)為 0 時(shí),則代表兩個(gè)簇中的樣本相似度一致,兩個(gè)簇本應(yīng)該是一個(gè)簇。
語(yǔ)法:
from sklearn.metrics import silhouette_score
# 返回所有樣本的輪廓系數(shù)的均值
from sklearn.metrics import silhouette_samples
# 返回的是數(shù)據(jù)集中每個(gè)樣本自己的輪廓系數(shù)
silhouette_score(X,y_pred)
silhouette_score(X,cluster_.labels_)
silhouette_samples(X,y_pred)
例:
L = []
for i in range(2, 20):
k = i
kmeans = KMeans(n_clusters=i)
kmeans.fit(X)
L.append([i, silhouette_score(X, kmeans.labels_)])
a = pd.DataFrame(L)
a.columns = ['k', '輪廓系數(shù)']
plt.figure(figsize=(8, 5), dpi=70)
plt.plot(a.k, a.輪廓系數(shù),'gp-')
plt.xticks(a.k)
plt.xlabel('k')
plt.ylabel('輪廓系數(shù)')
plt.title('輪廓系數(shù)確定最佳的K值',fontdict={'fontsize':15})
輸出結(jié)果:
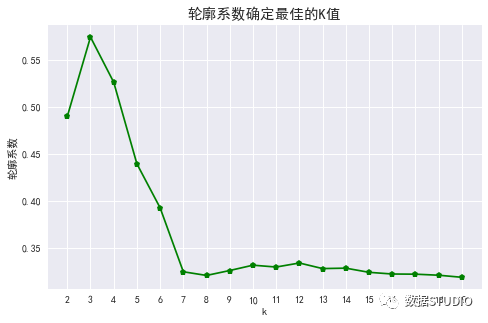
輪廓系數(shù)看出,k=3時(shí)輪廓系數(shù)最大,肘部法的拐點(diǎn)亦是k=3,從數(shù)據(jù)集可視化圖(文末案例)中也能看出數(shù)據(jù)集可以清洗分割3個(gè)簇(雖然初始創(chuàng)建了四個(gè)簇,但上面兩個(gè)簇邊界并不清晰,幾乎連到一起)。
輪廓系數(shù)有很多優(yōu)點(diǎn),它在有限空間中取值,使得我們對(duì)模型的聚類效果有一個(gè)"參考"。并且輪廓系數(shù)對(duì)數(shù)據(jù)的分布沒(méi)有假設(shè),因此在很多數(shù)據(jù)集上都表現(xiàn)良好。但它在每個(gè)簇的分割比較清洗時(shí)表現(xiàn)最好。
其它評(píng)估指標(biāo)
| 評(píng)估指標(biāo) | sklearn.metrics |
|---|---|
| 卡林斯基-哈拉巴斯指數(shù) Calinski-Harabaz Index | calinski_harabaz_score (X, y_pred) |
| 戴維斯-布爾丁指數(shù) Davies-Bouldin | davies_bouldin_score (X, y_pred) |
| 權(quán)變矩陣 Contingency | cluster.contingency_matrix (X, y_pred) |
這里簡(jiǎn)單介紹卡林斯基-哈拉巴斯指數(shù),有 個(gè)簇的聚類而言, Calinski-Harabaz指數(shù)寫作如下公式:
其中為數(shù)據(jù)集中的樣本量,為簇的個(gè)數(shù)(即類別的個(gè)數(shù)), 是組間離散矩陣,即不同簇之間的協(xié)方差矩陣, 是簇內(nèi)離散矩陣,即一個(gè)簇內(nèi)數(shù)據(jù)的協(xié)方差矩陣,而表示矩陣的跡。在線性代數(shù)中,一個(gè)矩陣的主對(duì)角線(從左上方至右下方的對(duì)角線)上各個(gè)元素的總和被稱為矩陣A的跡(或跡數(shù)),一般記作。
數(shù)據(jù)之間的離散程度越高,協(xié)方差矩陣的跡就會(huì)越大。組內(nèi)離散程度低,協(xié)方差的跡就會(huì)越小,也就越小,同時(shí),組間離散程度大,協(xié)方差的的跡也會(huì)越大,就越大,因此Calinski-harabaz指數(shù)越高越好。
雖然calinski-Harabaz指數(shù)沒(méi)有界,在凸型的數(shù)據(jù)上的聚類也會(huì)表現(xiàn)虛高。但是比起輪廓系數(shù),其計(jì)算非常快速。
案例
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
import pandas as pd
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=6000, centers=4, cluster_std = 2.5, n_features=2,center_box=(-12.0, 12.0),
random_state=42)
data = pd.DataFrame(X)
fig, axes = plt.subplots(3, 2)
fig.set_size_inches(18, 27)
n_clusters = 2
for i in range(3):
for j in range(2):
n_clusters = n_clusters
clusterer = KMeans(n_clusters=n_clusters, random_state=10).fit(X)
cluster_labels = clusterer.labels_
silhouette_avg = silhouette_score(X, cluster_labels)
print("For n_clusters =", n_clusters,
"The average silhouette_score is :", silhouette_avg)
sample_silhouette_values = silhouette_samples(X, cluster_labels)
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
axes[i,j].scatter(X[:, 0], X[:, 1]
,marker='o'
,s=8
,c=colors
)
centers = clusterer.cluster_centers_
axes[i,j].scatter(centers[:, 0], centers[:, 1], marker='x',
c="red", alpha=1, s=200)
axes[i,j].set_title(f"The visualization of the clustered data when n_Clusters = {n_clusters}.")
axes[i,j].set_xlabel("Feature space for the 1st feature")
axes[i,j].set_ylabel("Feature space for the 2nd feature")
axes[i,j].text(0,-17,f"The average silhouette_score is :\n\n{silhouette_avg}",fontsize=10)
n_clusters += 1
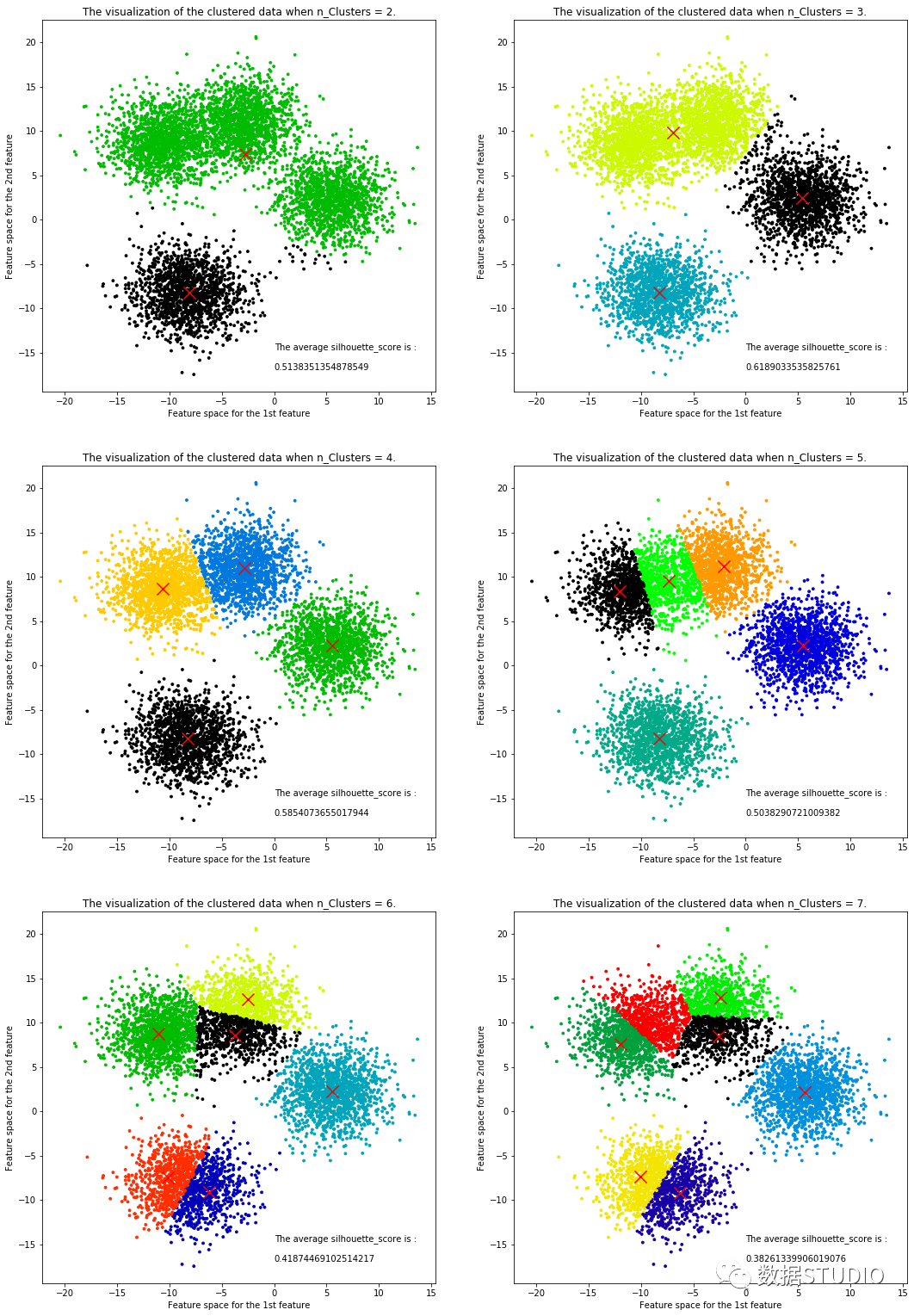
plt.show()輸出結(jié)果:
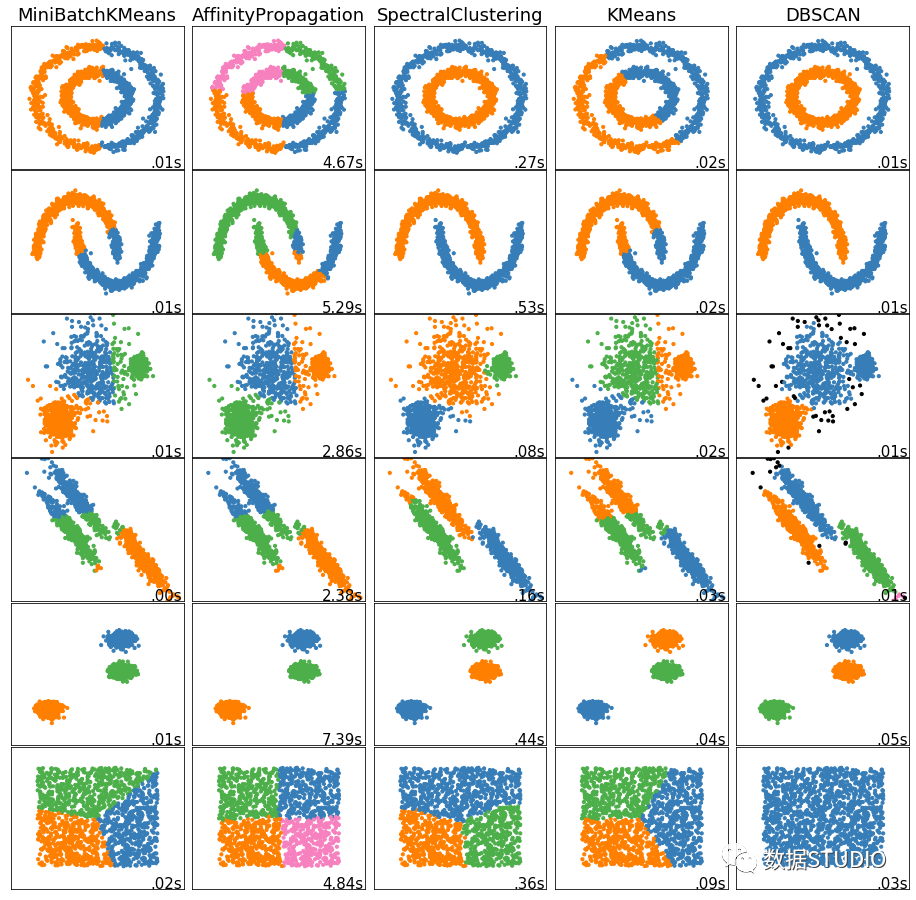
擴(kuò)展--其他聚類算法
DBSCAN
從向量數(shù)組或距離矩陣執(zhí)行DBSCAN聚類。
一種基于密度的帶有噪聲的空間聚類 。它將簇定義為密度相連的點(diǎn)的最大集合,能夠把具有足夠高密度的區(qū)域劃分為簇,并可在噪聲的空間數(shù)據(jù)集中發(fā)現(xiàn)任意形狀的聚類。
基于密度的空間聚類與噪聲應(yīng)用。尋找高密度的核心樣本,并從中擴(kuò)展星團(tuán)。適用于包含相似密度的簇的數(shù)據(jù)。
DBSCAN算法將聚類視為由低密度區(qū)域分隔的高密度區(qū)域。由于這種相當(dāng)通用的觀點(diǎn),DBSCAN發(fā)現(xiàn)的集群可以是任何形狀,而k-means假設(shè)集群是凸形的。DBSCAN的核心組件是核心樣本的概念,即位于高密度區(qū)域的樣本。因此,一個(gè)集群是一組彼此接近的核心樣本(通過(guò)一定的距離度量)和一組與核心樣本相近的非核心樣本(但它們本身不是核心樣本)。算法有兩個(gè)參數(shù),min_samples和eps,它們正式定義了我們所說(shuō)的密集。較高的min_samples或較低的eps表示較高的密度需要形成一個(gè)集群。
根據(jù)定義,任何核心樣本都是集群的一部分。任何非核心樣本,且與核心樣本的距離至少為eps的樣本,都被算法認(rèn)為是離群值。
而主要控制參數(shù)min_samples寬容的算法對(duì)噪聲(在嘈雜和大型數(shù)據(jù)集可能需要增加此參數(shù)),選擇適當(dāng)?shù)膮?shù)eps至關(guān)重要的數(shù)據(jù)集和距離函數(shù),通常不能在默認(rèn)值。它控制著點(diǎn)的局部鄰域。如果選擇的數(shù)據(jù)太小,大多數(shù)數(shù)據(jù)根本不會(huì)聚集在一起(并且標(biāo)記為-1表示"噪音")。如果選擇太大,則會(huì)導(dǎo)致關(guān)閉的集群合并為一個(gè)集群,并最終將整個(gè)數(shù)據(jù)集作為單個(gè)集群返回。
例:
>>> from sklearn.cluster import DBSCAN
>>> import numpy as np
>>> X = np.array([[1, 2], [2, 2], [2, 3],
... [8, 7], [8, 8], [25, 80]])
>>> clustering = DBSCAN(eps=3, min_samples=2).fit(X)
>>> clustering.labels_
array([ 0, 0, 0, 1, 1, -1])
>>> clustering
DBSCAN(eps=3, min_samples=2)
eps float, default=0.5
兩個(gè)樣本之間的最大距離,其中一個(gè)樣本被認(rèn)為是相鄰的。這不是集群內(nèi)點(diǎn)的距離的最大值,這是為您的數(shù)據(jù)集和距離函數(shù)選擇的最重要的DBSCAN參數(shù)。
min_samples int, default=5
被視為核心點(diǎn)的某一鄰域內(nèi)的樣本數(shù)(或總權(quán)重)。這包括點(diǎn)本身。
更多DBSCAN聚類請(qǐng)參見(jiàn)
https://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html#sklearn.cluster.DBSCAN
層次聚類
層次聚類Hierarchical Clustering 通過(guò)計(jì)算不同類別數(shù)據(jù)點(diǎn)間的相似度來(lái)創(chuàng)建一棵有層次的嵌套聚類樹(shù)。在聚類樹(shù)中,不同類別的原始數(shù)據(jù)點(diǎn)是樹(shù)的最低層,樹(shù)的頂層是一個(gè)聚類的根節(jié)點(diǎn)。創(chuàng)建聚類樹(shù)有自下而上合并和自上而下分裂兩種方法。
層次聚類的合并算法通過(guò)計(jì)算兩類數(shù)據(jù)點(diǎn)間的相似性,對(duì)所有數(shù)據(jù)點(diǎn)中最為相似的兩個(gè)數(shù)據(jù)點(diǎn)進(jìn)行組合,并反復(fù)迭代這一過(guò)程。
簡(jiǎn)單來(lái)說(shuō) 通過(guò)計(jì)算每一個(gè)類別的數(shù)據(jù)點(diǎn)與所有數(shù)據(jù)點(diǎn)之間的歐式距離來(lái)確定它們之間的相似性,距離越小,相似度越高 。并將距離最近的兩個(gè)數(shù)據(jù)點(diǎn)或類別進(jìn)行組合,生成聚類樹(shù)。
例:
>>> from sklearn.cluster import AgglomerativeClustering
>>> import numpy as np
>>> X = np.array([[1, 2], [1, 4], [1, 0],
... [4, 2], [4, 4], [4, 0]])
>>> clustering = AgglomerativeClustering().fit(X)
>>> clustering
AgglomerativeClustering()
>>> clustering.labels_
array([1, 1, 1, 0, 0, 0])
層次化聚類是一種通用的聚類算法,它通過(guò)合并或分割來(lái)構(gòu)建嵌套的聚類。集群的層次結(jié)構(gòu)表示為樹(shù)(或樹(shù)狀圖)。樹(shù)的根是收集所有樣本的唯一集群,葉子是只有一個(gè)樣本的集群。
聚類對(duì)象使用自底向上的方法執(zhí)行分層聚類: 每個(gè)觀察從它自己的聚類開(kāi)始,然后聚類依次合并在一起。連接標(biāo)準(zhǔn)決定了用于合并策略的度量。
最大或完全連接使簇對(duì)觀測(cè)之間的最大距離最小。 平均連接使簇對(duì)的所有觀測(cè)值之間的平均距離最小化。 單連接使簇對(duì)的最近觀測(cè)值之間的距離最小。 當(dāng)與連通性矩陣聯(lián)合使用時(shí),團(tuán)聚向量聚合也可以擴(kuò)展到大量的樣本,但是當(dāng)樣本之間不加連通性約束時(shí),計(jì)算開(kāi)銷就大了:它在每一步都考慮所有可能的合并。
更多層次聚類請(qǐng)參見(jiàn)
https://scikit-learn.org/stable/modules/generated/sklearn.cluster.AgglomerativeClustering.html#sklearn.cluster.AgglomerativeClustering
附錄
KMeans參數(shù)
n_clusters int, default=8
要聚成的簇?cái)?shù),以及要生成的質(zhì)心數(shù)。
init {‘k-means++’, ‘random’, ndarray, callable}, default=’k-means++’
這是初始化質(zhì)心的方法,輸入
"k- means++": 一種為K均值聚類選擇初始聚類中心的聰明的辦法,以加速收斂。如果輸入了n維數(shù)組,數(shù)組的形狀應(yīng)該是(n_clusters,n_features)并給出初始質(zhì)心。n_init int, default=10
使用不同的質(zhì)心隨機(jī)初始化的種子來(lái)運(yùn)行
KMeans算法的次數(shù)。最終結(jié)果會(huì)是基于Inertia來(lái)計(jì)算的n_init次連續(xù)運(yùn)行后的最佳輸出。max_iter int, default=300
單次運(yùn)行的
KMeans算法的最大迭代次數(shù)。tol float, default=1e-4
兩次迭代間
Inertia下降的量,如果兩次迭代之間Inertia下降的值小于tol所設(shè)定的值,迭代就會(huì)停下。precompute_distances {‘a(chǎn)uto’, True, False}, default=’auto’
預(yù)計(jì)算距離(更快,但需要更多內(nèi)存)。
'auto': 如果n_samples * n_clusters > 1200萬(wàn),不要預(yù)先計(jì)算距離。這對(duì)應(yīng)于使用雙精度來(lái)學(xué)習(xí),每個(gè)作業(yè)大約100MB的內(nèi)存開(kāi)銷。
True: 始終預(yù)先計(jì)算距離。False:從不預(yù)先計(jì)算距離。verbose int, default=0
計(jì)算中的詳細(xì)模式。
random_state int, RandomState instance, default=None
確定質(zhì)心初始化的隨機(jī)數(shù)生成。使用
int可以是隨機(jī)性更具有確定性。copy_x bool, default=True
在預(yù)計(jì)算距離時(shí),若先中心化數(shù)據(jù),距離的預(yù)計(jì)算會(huì)更加準(zhǔn)確。如果
copy_x為True(默認(rèn)值),則不會(huì)修改原始數(shù)據(jù),確保特征矩陣X是c-contiguous。如果為False,則對(duì)原始數(shù)據(jù)進(jìn)行修改,在函數(shù)返回之前放回原始數(shù)據(jù),但可以通過(guò)減去數(shù)據(jù)平均值,再加上數(shù)據(jù)平均值,引入較小的數(shù)值差異。注意,如果原始數(shù)據(jù)不是c -連續(xù)的,即使copy_x為False,也會(huì)復(fù)制,這可能導(dǎo)致KMeans計(jì)算量顯著變慢。如果原始數(shù)據(jù)是稀疏的,但不是CSR格式的,即使copy_x是False的,也會(huì)復(fù)制一份。n_jobs int, default=None
用于計(jì)算的作業(yè)數(shù)。計(jì)算每個(gè)
n_init時(shí)并行作業(yè)數(shù)。這個(gè)參數(shù)允許
KMeans在多個(gè)作業(yè)線上并行運(yùn)行。給這個(gè)參數(shù)正值n_jobs,表示使用n_jobs條處理器中的線程。值-1表示使用所用可用的處理器。值-2表示使用所有可能的處理器-1個(gè)處理器,以此類推。并行化通常以內(nèi)存為代價(jià)增加計(jì)算(這種情況下,需要存儲(chǔ)多個(gè)質(zhì)心副本,每個(gè)作業(yè)一個(gè))algorithm {“auto”, “full”, “elkan”}, default=”auto”
使用
KMeans算法。經(jīng)典的EM風(fēng)格的算法是"full"的。通過(guò)使用三角不等式,"elkan"變異在具有定義明確的集群的數(shù)據(jù)上更有效。然而,由于分配了額外的形狀數(shù)組(n_samples、n_clusters),它會(huì)占用更多的內(nèi)存。目前,"auto"為密集數(shù)據(jù)選擇"elkan"為稀疏數(shù)據(jù)選擇"full"。
KMeans屬性
cluster_centers_ ndarray of shape (n_clusters, n_features)
收斂到的質(zhì)心坐標(biāo)。如果算法在完全收斂之前已停止(受到'
tol'和'max_iter'參數(shù)的控制),這些返回的內(nèi)容將與'labels_'中反應(yīng)出的聚類結(jié)果不一致。labels_ ndarray of shape (n_samples,)
每個(gè)樣本對(duì)應(yīng)的標(biāo)簽。
inertia_ float
每個(gè)樣本點(diǎn)到它們最近的簇中心的距離的平方的和,又叫做"簇內(nèi)平方和"。
n_iter_ int
實(shí)際迭代的次數(shù)。
點(diǎn)贊+留言+轉(zhuǎn)發(fā),就是對(duì)我最大的支持啦~
--End--
文章點(diǎn)贊超過(guò)100+
我將在個(gè)人視頻號(hào)直播(老表Max)
帶大家一起進(jìn)行項(xiàng)目實(shí)戰(zhàn)復(fù)現(xiàn)
掃碼即可加我微信
老表朋友圈經(jīng)常有贈(zèng)書/紅包福利活動(dòng)
點(diǎn)擊上方卡片關(guān)注公眾號(hào),回復(fù):1024 領(lǐng)取最新Python學(xué)習(xí)資源 學(xué)習(xí)更多: 整理了我開(kāi)始分享學(xué)習(xí)筆記到現(xiàn)在超過(guò)250篇優(yōu)質(zhì)文章,涵蓋數(shù)據(jù)分析、爬蟲(chóng)、機(jī)器學(xué)習(xí)等方面,別再說(shuō)不知道該從哪開(kāi)始,實(shí)戰(zhàn)哪里找了 “點(diǎn)贊”就是對(duì)博主最大的支持