原理+代碼｜Python實現(xiàn) kmeans 聚類分析

聚類分析是研究分類問題的分析方法，是洞察用戶偏好和做用戶畫像的利器之一，也可作為其他數(shù)據(jù)分析任務(wù)的前置探索(如EDA)。上文的層次聚類算法在數(shù)據(jù)挖掘中其實并不常用，因為只是適用于小數(shù)據(jù)。所以我們引出了 K-Means 聚類法，這種方法計算量比較小。能夠理解 K-Means 的基本原理并將代碼用于實際業(yè)務(wù)案例是本文的目標(biāo)。下文將詳細介紹如何利用 Python 實現(xiàn)基于 K-Means 聚類的客戶分群，主要分為兩個部分：

• 詳細原理介紹
• Python代碼實戰(zhàn)

上一篇層次聚類的推文中提到「既然它們能被看成是一類的，所以要么它們距離近，要么它們或多或少有共同的特征」。為了能夠更好地深入淺出，我們像上次那樣調(diào)整一下學(xué)習(xí)順序，將數(shù)學(xué)公式往后放，先從聚類過程與結(jié)果入手。注意，本文先以樣本之間的距離為聚類指標(biāo)。

K-Means 聚類的目標(biāo)就一句話「將 n 個觀測數(shù)據(jù)點按照一定標(biāo)準(zhǔn)劃分到 k 個聚類中」。至于這個標(biāo)準(zhǔn)怎么定奪以及如何判斷聚類結(jié)果好壞等問題，文章后半段會提及。

K-Means 聚類的步驟用這一張圖就可以表達出來。（這里的 k 為 2，即分成兩類）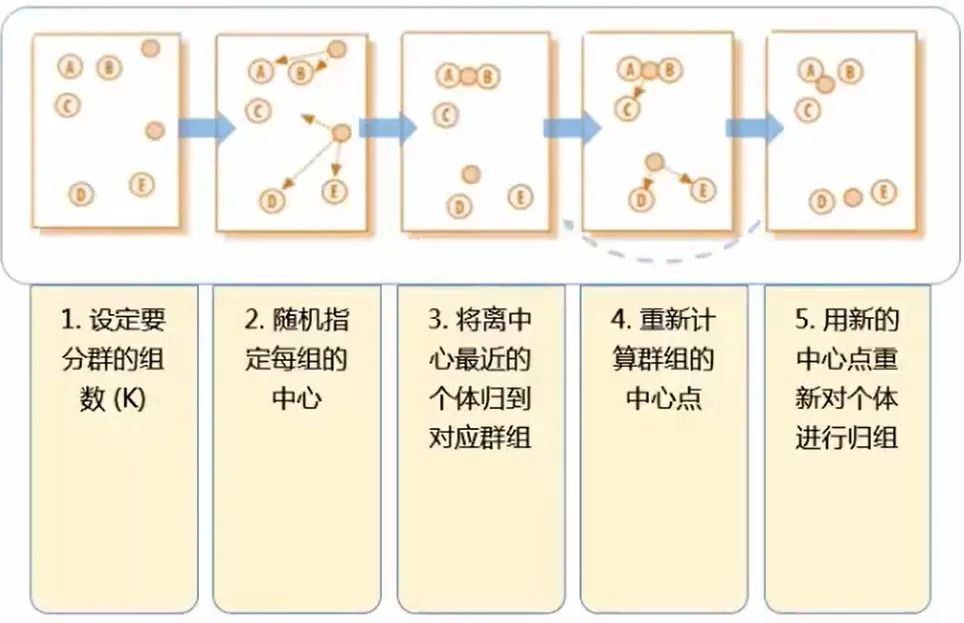

2.1 關(guān)于kmeans的一些問題

問：在第二步的隨機指定每組的中心 這個步驟中，明擺著 ABC 為一類，DE 為一類 才是最正確的分類方式，畢竟肉眼就可以判斷距離了，為什么指定每組的中心后反倒分類錯誤了呢？（第二步是將 AB 一類，CDE 一類）？

答：別著急，K-Means 算法并不求一步就完全分類正確。第二步到第三步的過程被稱為“中心迭代“。一開始是隨機的指定每組的中心，這個中心可能是有偏頗的，所以第三步是用每個類的中心來代替第二步中隨即指定的中心。接下來再計算每個點到中心的距離，就會發(fā)現(xiàn) C 這個點其實是離上面的中心更近（AB 一類，DE 一類本來就分類正確了，只是 C 出現(xiàn)了分類失誤）

問：圖中經(jīng)過第四步后其實就已經(jīng)劃分出了正確的分類，第五步還有什么用呢？

答：第四步到第五步這個過程跟第二到第三步一樣，也叫 “ 中心迭代 ”，即將新分好的正確的類的中心作為群組的中心點。這樣才能為下一步的分類做準(zhǔn)備，畢竟數(shù)據(jù)量并不只是圖中的五個點，這一套(五步)流程也不是只運行一次就能完成分類，需要不斷重復(fù)，最終的結(jié)果便是不會再有點像 C 那樣更換分類的情況。

問：第一步要計算幾次距離？（k=2）

答：需要計算 10 次距離，隨即指定的兩個中心點到每一個已知點的距離：中心1，2 分別到點 ABCDE 的距離。其實也就是 n 個點，分成 k 類時，需要計算 n×k 次。

問：第一步用層次聚類法也是 10 次，為什么還說 K-Means 是一個計算量較小的方法呢？

答：對第一步使用層次聚類法的計算次數(shù)為：Cn2（（C52 = (54)/2）），即計算兩兩點之間的距離，然后再比較篩選，即：n(n-1) / 2 = 54 / 2 = 10 次，但這只是小的數(shù)據(jù)樣本，如果樣本量巨大呢（同樣還是 k 為 2 時）？那么 K-Means 的 n*k 與層次聚類法的 Cn2 的復(fù)雜度圖比較便是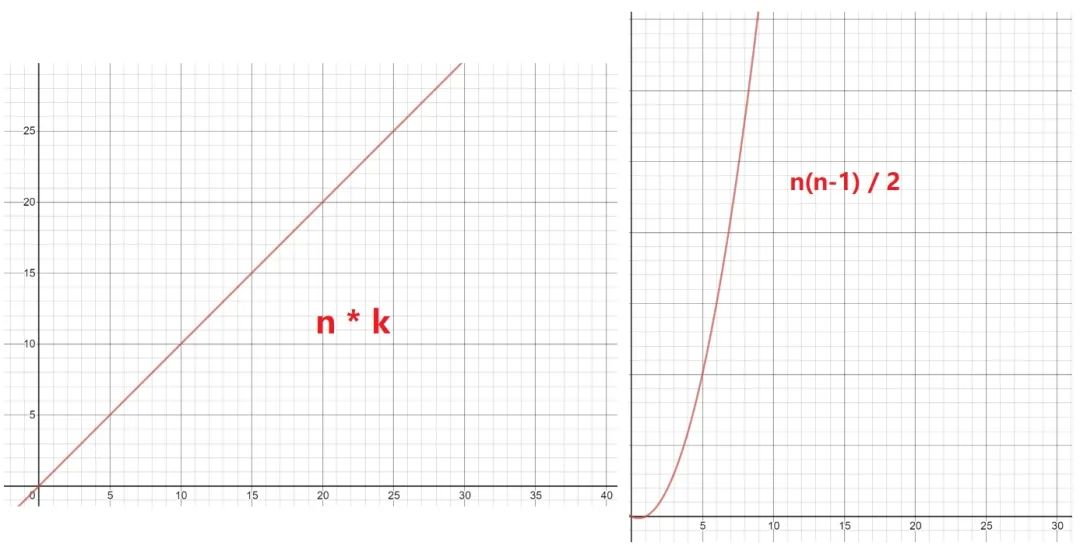：數(shù)據(jù)量一旦開始增加，層級聚類法的計算復(fù)雜程度便呈指數(shù)級增長。

問：K-Means 的不足？

答：K-Means 最顯著的缺點便是 k 的個數(shù)不好確定，但在商業(yè)數(shù)據(jù)挖掘上，這個缺點其實不一定難避免。因為商業(yè)數(shù)據(jù)挖掘的 k-means 聚類方法中，k 大部分都在 2 ~ 12 這個范圍，所以只需要做 9 次，然后看哪種效果最好即可。

2.2 K-Means 的要點

要點1：預(yù)先處理變量的缺失值、異常值 要點2：變量標(biāo)準(zhǔn)化 要點3：不同維度的變量，相關(guān)性盡量低 要點4：如何決定合適的分群個數(shù)？·

主要推薦輪廓系數(shù)（Silhouette Coeficient），并結(jié)合以下注意事項：

• 分群結(jié)果的穩(wěn)定性

• 重復(fù)多次分群，看結(jié)果是否穩(wěn)定

• 分群結(jié)果是否有好解釋的商業(yè)意義

也有一種相對沒那么嚴謹?shù)姆诸惙椒ǎ@種方法通常會分 5~8 類，這樣既能反映工作量（給領(lǐng)導(dǎo)看），又不至于太累（分出 12 類，還要對每一類的特征進行探索，描述性統(tǒng)計分析等）

2.3 輪廓系數(shù)

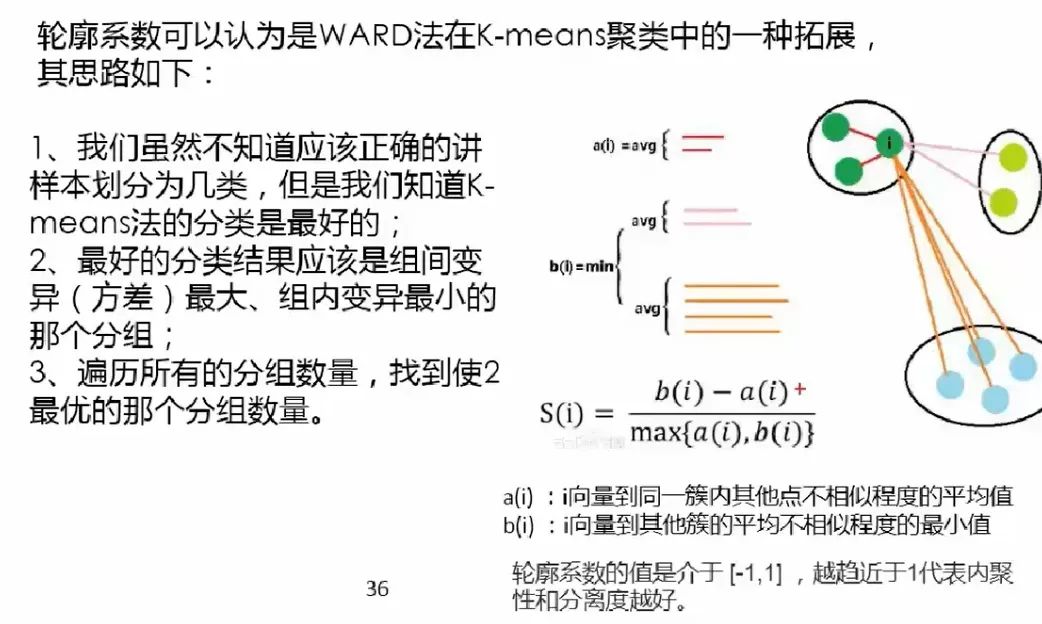
最好的分類結(jié)果：不同組之間的差距越大越好，同組內(nèi)的樣本差距越小越好。這樣才能更好的體現(xiàn)物以類聚的思想（e.g: 同一類人的三觀非常一致，不同類的人之間三觀相差甚遠）。因為組內(nèi)差異為零的話，a(i) 便無限接近于0，公式分子便為 b(i)，分母 max{0, b(i)} = b(i)，所以結(jié)果為 b(i) / b(i) = 1，即越趨近于 1 代表組內(nèi)聚類性和組間的分離度越好。

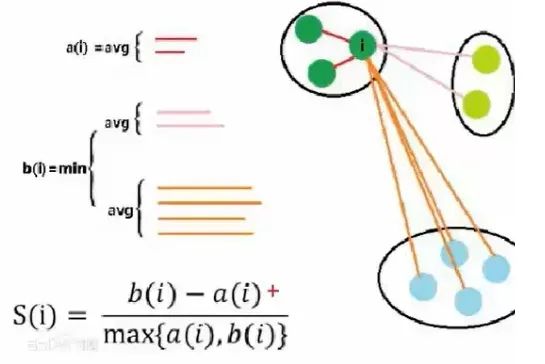
輪廓系數(shù)其實非常難求，組內(nèi)的(a(i))好算，b(i) 非常難計算，而且還要每個點都要同不同組里面的所有點進行計算，所以輪廓系數(shù)在實操的時候樣本量的大小需要控制，一般幾千就行了，幾萬的話就太難計算了；換言之，輪廓系數(shù)一般也是在探索的時候用，比如分層抽樣后對 k 的取值進行探索。這也再次呼應(yīng)了前兩段提到的 K-Means 方法的 k 難以直接通過數(shù)學(xué)公式求得的的這一特點。

2.4 K-Means 聚類的兩種用法

1、發(fā)現(xiàn)異常情況：如果不對數(shù)據(jù)進行任何形式的轉(zhuǎn)換，只是經(jīng)過中心標(biāo)準(zhǔn)化或級差標(biāo)準(zhǔn)化就進行快速聚類，會根據(jù)數(shù)據(jù)分布特征得到聚類結(jié)果。這種聚類會將極端數(shù)據(jù)聚為幾類。這種方法適用于統(tǒng)計分析之前的異常值剔除，對異常行為的挖掘，比如：監(jiān)控銀行賬戶是否有洗錢行為、監(jiān)控POS機是有從事套現(xiàn)、監(jiān)控某個終端是否是電話卡養(yǎng)卡客戶等等。

2、將個案數(shù)據(jù)做劃分：出于客戶細分目的的聚類分析一般希望聚類結(jié)果為大致平均的幾大類，因此需要將數(shù)據(jù)進行轉(zhuǎn)換比如使用原始變量的百分位秩、Turkey正態(tài)評分、對數(shù)轉(zhuǎn)換等等。在這類分析中數(shù)據(jù)的具體數(shù)值并沒有太多的意義，重要的是相對位置。這種方法適用場景包括客戶消費行為聚類、客戶積分使用行為聚類等等。

如果變量比較多比如 10 個左右，變量間的相關(guān)性又比較高，就應(yīng)該做個因子分析或者稀疏主成分分析，因為 K-Means 要求不同維度的變量相關(guān)性盡量低。（本系列的推文：原理+代碼｜Python基于主成分分析的客戶信貸評級實戰(zhàn)）

那如果數(shù)據(jù)右偏嚴重，K-Means 聚類會出現(xiàn)什么情況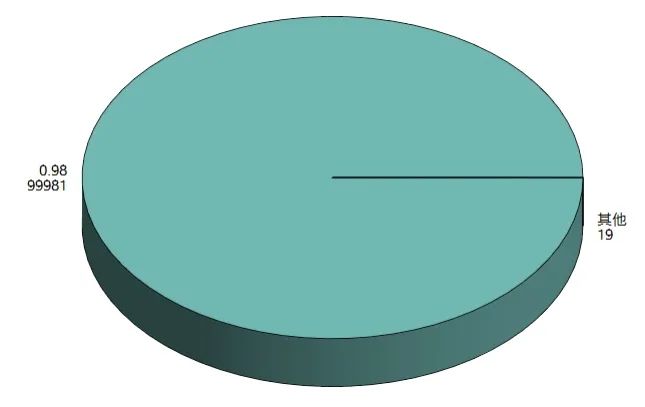？如果不經(jīng)過任何處理，則聚類出來的結(jié)果便是如上圖那樣，出現(xiàn) ”絕大部分客戶屬于一類，很少量客戶屬于另外一類“ 的情況，這就失去了客戶細分的意義（除非你是為了檢測異常值），因為有時候我們希望客戶能夠被均勻的分成幾類（許多領(lǐng)導(dǎo)和甲方的需求為均勻的聚類，這是出于管理的需求）原始數(shù)據(jù)本來就是右偏的，幾種標(biāo)準(zhǔn)化方式之后其實也還是右偏的...，我們在學(xué)校學(xué)習(xí)統(tǒng)計學(xué)或聚類方法的時候，所用數(shù)據(jù)大多是來自自然科學(xué)的，所以分布情況都比較“完美”，很少出現(xiàn)較強的偏態(tài)分布。而現(xiàn)實生活與工作中的數(shù)據(jù)，如金融企業(yè)等，拿到的數(shù)據(jù)大多右偏嚴重。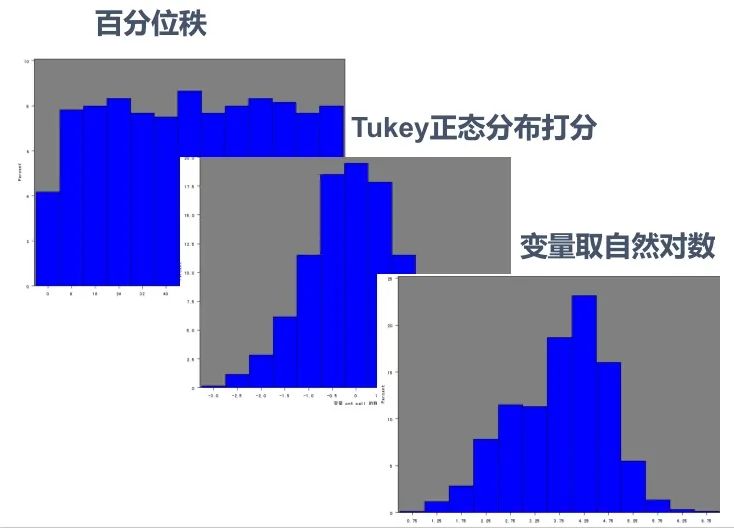上圖是能夠強迫將右偏數(shù)據(jù)轉(zhuǎn)換成均勻分布的幾種方法。但通常回歸算法時的右偏處理才會使用變量取自然對數(shù)的方法，聚類算法常用 Tukey 正態(tài)分布打分的方式來處理右偏數(shù)據(jù)。

2.5 變量轉(zhuǎn)換小結(jié)

非對稱變量在聚類分析中選用百分位秩和Tukey正態(tài)分布打分比較多；在回歸分析中取對數(shù)比較多。因為商業(yè)上的聚類模型關(guān)心的客戶的排序情況，回歸模型關(guān)心的是其具有經(jīng)濟學(xué)意義，對數(shù)表達的是百分比的變化。

2.6 使用決策樹做聚類后的客戶分析

聚類算法還能與決策樹算法一起用（期待臉(☆▽☆)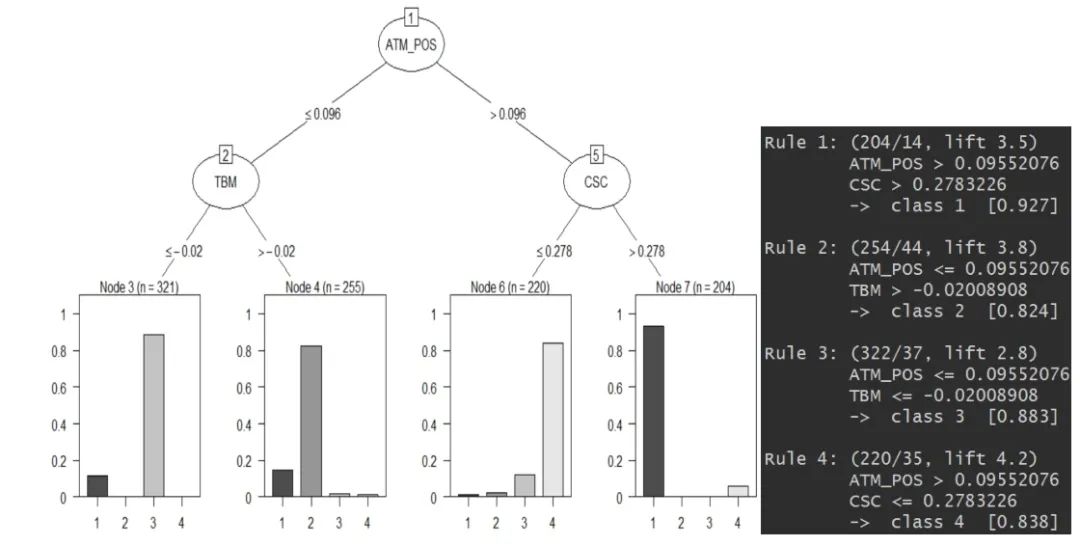）？輪廓系數(shù)可以為我們做 K-Means 聚類的時候提供一個 k 的參考值，而初步聚類后，我們便有了 Y，即每個數(shù)據(jù)樣本所對應(yīng)的類別。這時候我們畫棵決策樹（可以結(jié)合使用高端一些的決策樹可視化方式），如果底端的葉子所呈現(xiàn)出的數(shù)據(jù)分類是某一類較多，其余類偏少，這樣便表示這個 k 值是一個比較好的選擇。（每一類都相對較純，沒有雜質(zhì)）

本次代碼實戰(zhàn)我們將使用已經(jīng)經(jīng)過前文主成分分析處理過的有關(guān)銀行客戶的數(shù)據(jù)集：

• CSC：counter service for customer -- 選擇柜臺服務(wù)的客戶
• ATM_POS: 使用 ATM 和 POS 服務(wù)的客戶
• TBM：選擇有償服務(wù)的客戶

import pandas as pd

# df 為清洗好的數(shù)據(jù)
df = pd.read_csv('data_clean.csv')
df.head()
這里每個變量所在列的具體數(shù)值可先不做探究

這里每個變量所在列的具體數(shù)值可先不做探究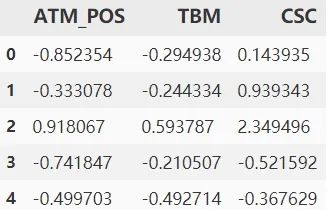

3.1 K-Means 聚類的第一種方式

不進行變量分布的正太轉(zhuǎn)換--用于尋找異常值

# 使用k-means聚類
## 1.1 k-means聚類的第一種方式：不進行變量分布的正態(tài)轉(zhuǎn)換--用于尋找異常值

# 1、查看變量的偏度
var = ["ATM_POS","TBM","CSC"]  # var: variable-變量
skew_var = {}
for i in var:
    skew_var[i]=abs(df[i].skew()) # .skew() 求該變量的偏度
    skew=pd.Series(skew_var).sort_values(ascending=False)
skew

可以看出 TBM 這個變量的偏度已經(jīng)超標(biāo)，很可能會影響到后續(xù)的分類進行k-means聚類

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3) # n_clusters=3 表示聚成3類

result = kmeans.fit(df)
result

與隨機森林，決策樹等算法一樣，KMeans 函數(shù)中的參數(shù)眾多，這里不具體解釋了，可查閱官方文檔.join() 表示橫向拼接

# 對分類結(jié)果進行解讀
model_data_l = df.join(pd.DataFrame(result.labels_)) 
                            # .labels_ 表示這一個數(shù)據(jù)點屬于什么類
model_data_l = model_data_l.rename(columns={0: "clustor"})
model_data_l.sample(10)

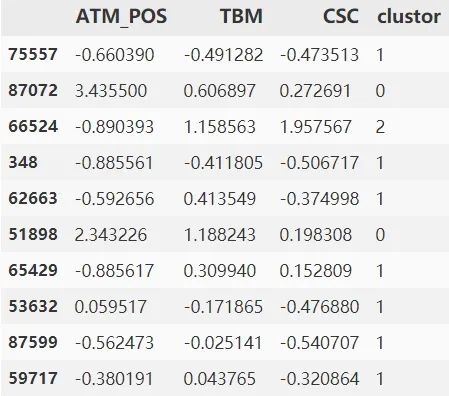繪制餅圖呈現(xiàn)每一類的比例

# 餅圖呈現(xiàn)
import matplotlib
get_ipython().magic('matplotlib inline')
model_data_l.clustor.value_counts().plot(kind = 'pie') 
# 自然就能發(fā)現(xiàn)出現(xiàn)分類很不平均的現(xiàn)象

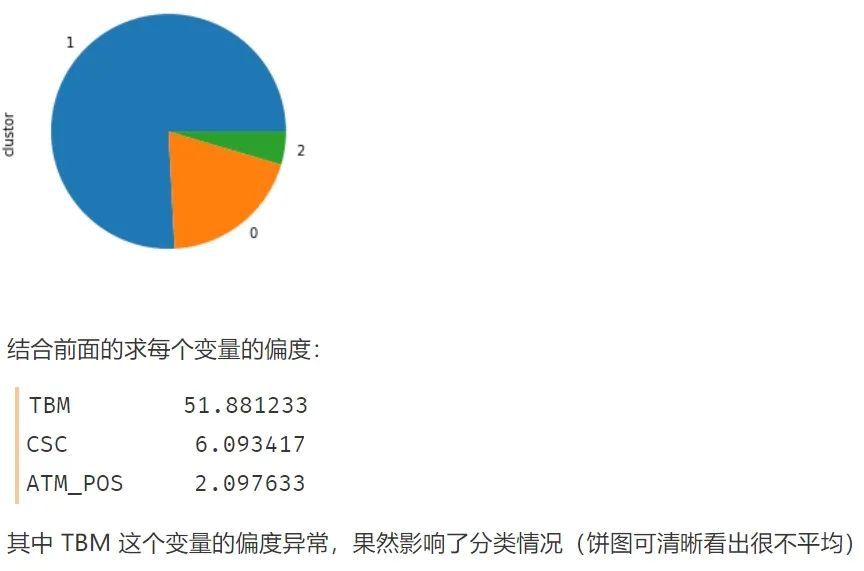
3.2 k-means聚類的第二種方式

進行變量分布的正態(tài)轉(zhuǎn)換--用于客戶細分

# 進行變量分布的正態(tài)轉(zhuǎn)換
import numpy as np
from sklearn import preprocessing
quantile_transformer = \
    preprocessing.QuantileTransformer(output_distribution='normal', 
                                      random_state=0) # 正態(tài)轉(zhuǎn)換

df_trans = quantile_transformer.fit_transform(df)
df_trans = pd.DataFrame(df_trans)  
 # 因為 .fit_transform 轉(zhuǎn)換出來的數(shù)據(jù)類型為 Series，
    ## 所以用 pandas 給 DataFrame 化一下

df_trans = df_trans.rename(columns={0: "ATM_POS", 1: "TBM", 2: "CSC"})
df_trans.head()

轉(zhuǎn)換的方式有很多種，每種都會涉及一些咋看起來比較晦澀的統(tǒng)計學(xué)公式,但請不要擔(dān)心，每種代碼其實都是比較固定的，這里使用 QT 轉(zhuǎn)換（每種轉(zhuǎn)換的原理和特點優(yōu)劣等可參考網(wǎng)絡(luò)資源）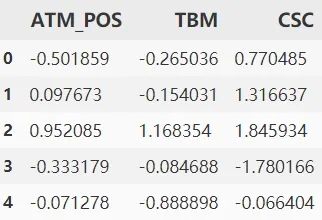

檢驗一下偏度：發(fā)現(xiàn)幾乎都為 0 了

var = ["ATM_POS","TBM","CSC"]
skew_var = {}

循環(huán)計算偏度：發(fā)現(xiàn)都差不多等于 0 了。

for i in var:
    skew_var[i] = abs(df_trans[i].skew())
    skew = pd.Series(skew_var).sort_values(ascending=False)
skew  # 字典顯示更方便

重復(fù)的聚類步驟，代碼可直接粘貼

kmeans = KMeans(n_clusters=4)  # 這次聚成 4 類
result = kmeans.fit(df_trans)

model_data_l = df_trans.join(pd.DataFrame(result.labels_))
model_data_l = model_data_l.rename(columns={0: "clustor"})
model_data_l.head()

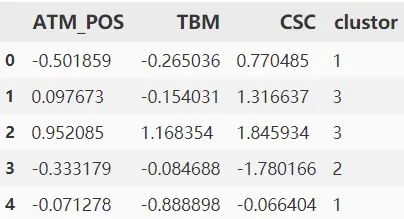再次使用餅圖呈現(xiàn)結(jié)果，發(fā)現(xiàn)每類的比例開始平均了。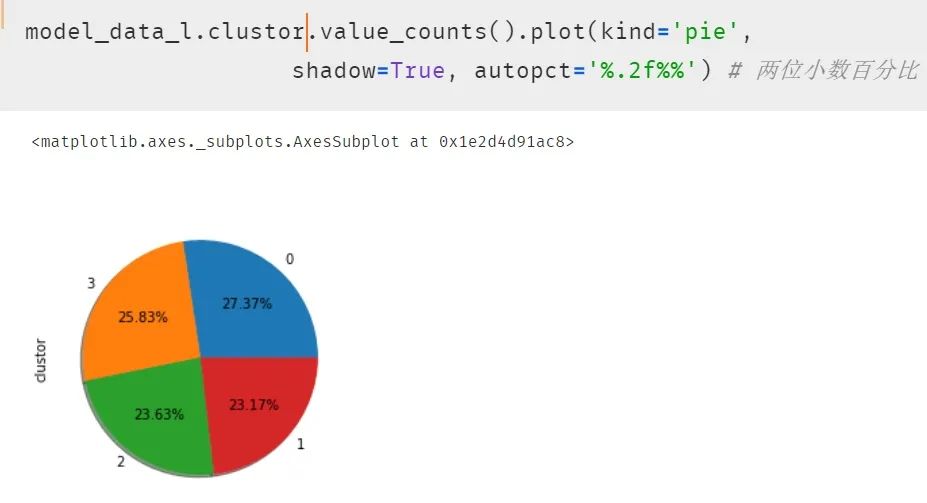

3.3 結(jié)果分析

最后對結(jié)果進行分析如下表

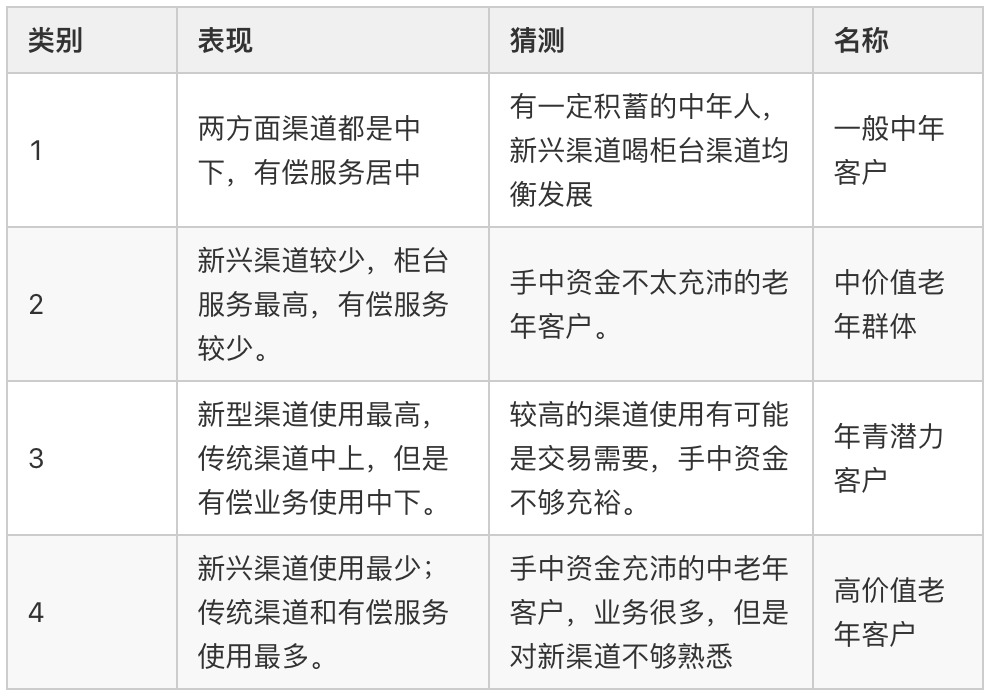
小結(jié)

對于不同場景，我們的使用聚類的方法也有所不同：

“

• 一般場景下的聚類：「變量歸一化  --> 分布轉(zhuǎn)換 --> 主成分 --> 聚類」
• 發(fā)現(xiàn)異常境況的聚類：「變量歸一化 --> 主成分 --> 聚類」

”

其實聚類模型對分析人員的業(yè)務(wù)修養(yǎng)要求較高，因為聚類結(jié)果好壞不是簡單的看統(tǒng)計指標(biāo)就可得出明確的答案。統(tǒng)計指標(biāo)是在所有的變量都符合某個假設(shè)條件才能表現(xiàn)良好的，而實際建模中很少能達到那種狀態(tài)；聚類的結(jié)果要做詳細的描述性統(tǒng)計，甚至作抽樣的客戶訪談，以了解客戶的真實情況，所以讓業(yè)務(wù)人員滿足客戶管理的目標(biāo)，是聚類的終極目標(biāo)。

PS：公號內(nèi)回復(fù)「Python」即可進入Python 新手學(xué)習(xí)交流群，一起 100 天計劃！

老規(guī)矩，兄弟們還記得么，右下角的 “在看” 點一下，如果感覺文章內(nèi)容不錯的話，記得分享朋友圈讓更多的人知道！

【代碼獲取方式】