效果

實(shí)現(xiàn)

整體思路

思路遵循以下幾步

• 初始化一個(gè)多邊形。
• 折疊后分割成兩個(gè)多邊形。
• 如果需要繼續(xù)分割，對(duì)場(chǎng)上的所有多邊形進(jìn)行折疊，折疊出新的多邊形的層級(jí)正好與原來(lái)的相反。

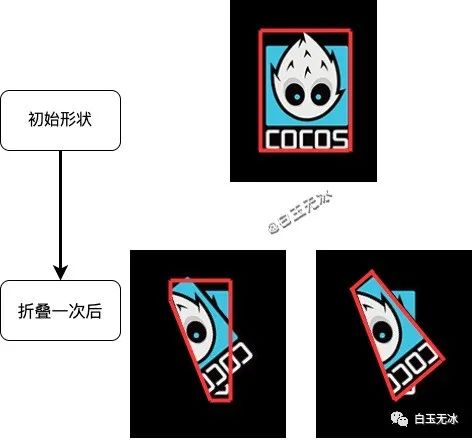
所以，所有的計(jì)算和渲染都可以轉(zhuǎn)換成對(duì)一個(gè)多邊形的操作。

為了簡(jiǎn)化計(jì)算，我們約定初始化的多邊形為凸多邊形。這么做有幾個(gè)好處。

• 折疊后生成的仍是凸多邊形，并且對(duì)于每個(gè)多邊形只會(huì)折疊出兩個(gè)凸多邊形
• 渲染時(shí)，分割凸多邊形為三角形特別方便，即能快速計(jì)算出頂點(diǎn)索引

計(jì)算

主要分為三塊

• 多邊形分割
• 線線交點(diǎn)
• 軸對(duì)稱

分割

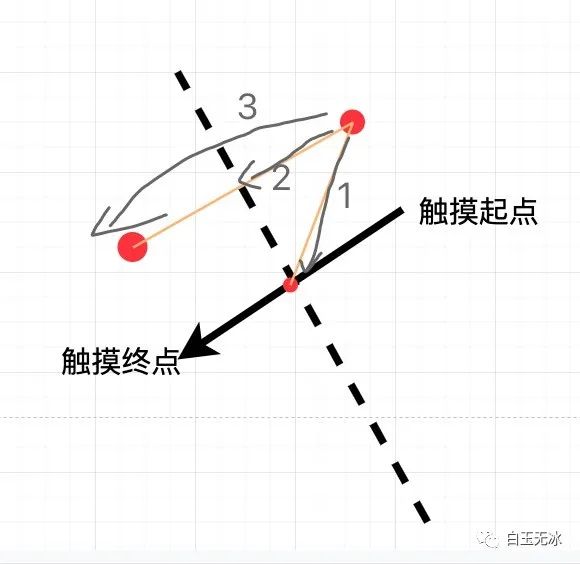
觀察觸摸方向和多邊形各個(gè)點(diǎn)的關(guān)系。

可以發(fā)現(xiàn)，觸摸方向 與 觸摸方向中點(diǎn)指向多邊形頂點(diǎn) 的夾角決定了分割后的多邊形的點(diǎn)。

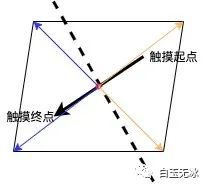
• 當(dāng)夾角大于90度時(shí)，該頂點(diǎn)正好是折疊多邊形的頂點(diǎn)。
• 當(dāng)夾角等于90度時(shí)，該頂點(diǎn)是兩個(gè)多邊形的頂點(diǎn)。
• 當(dāng)夾角小于90度時(shí)，該頂點(diǎn)是底部多邊形的頂點(diǎn)。

向量間的點(diǎn)積正好可以幫助我們判斷夾角問(wèn)題。

const dotValue = temp_v2_vector.dot(temp_v2_vector_3)
if (Math.abs(dotValue) === 0) {
    // 剛好在點(diǎn)上      
} else if (dotValue > 0) {
    // 在前面  
} else {
    // 在后面
}

交點(diǎn)

當(dāng)被分割的多邊形相鄰兩點(diǎn)與觸摸方向的夾角不同時(shí)（屬于兩個(gè)多邊形的點(diǎn)），需要計(jì)算觸摸向量的垂直線與該線段的交點(diǎn)。

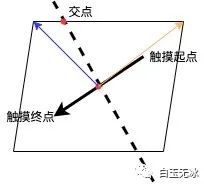
直線上的一點(diǎn)可以用點(diǎn)和向量表示。

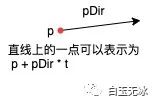
把兩直線的點(diǎn)表達(dá)式結(jié)合，再運(yùn)用克萊姆法則（Cramer's Rule）求出交點(diǎn)。

function linelinePoint(p1: Vec2, p1Dir: Vec2, p2: Vec2, p2Dir: Vec2) {
    const a1 = p1Dir.x, b1 = -p2Dir.x, c1 = p2.x - p1.x
    const a2 = p1Dir.y, b2 = -p2Dir.y, c2 = p2.y - p1.y
    const d = a1 * b2 - a2 * b1,
        d1 = c1 * b2 - c2 * b1,
        d2 = a1 * c2 - c1 * a2
    const t1 = d1 / d, t2 = d2 / d
    return [t1, t2]
}

這里計(jì)算的是比例t，這個(gè)t不僅可以用來(lái)求出頂點(diǎn)坐標(biāo)，也可以求出相交的紋理坐標(biāo)。

const posSpilt = Vec2(pos.x + dir.x * t1, pos.y + dir.y * t1)
const uvSpilt = Vec2(uv.x + uvdir.x * t1, uv.y + uvdir.y * t1)

對(duì)稱點(diǎn)

折疊多邊形的頂點(diǎn)正好是原多邊形頂點(diǎn)關(guān)于觸摸垂直軸對(duì)稱的點(diǎn)。

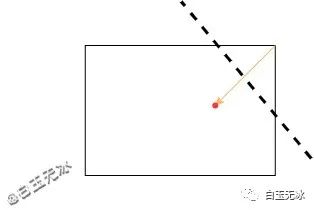
求對(duì)稱點(diǎn)同樣可以運(yùn)用向量計(jì)算。

1. 求出該頂點(diǎn)與中點(diǎn)的向量
2. 求出該點(diǎn)在觸摸方向的單位向量的投影(點(diǎn)乘)，這正好是距離的一半
3. 求出對(duì)稱點(diǎn)坐標(biāo)（距離乘方向向量+起始點(diǎn)坐標(biāo)）

Vec2.subtract(temp_v2_vector_4, temp_v2_pos, pos)
const dotLength = temp_v2_vector_4.dot(temp_v2_vector) * 2
temp_v2_pos_2.set((pos.x + temp_v2_vector.x * dotLength), pos.y + temp_v2_vector.y * dotLength)

渲染

渲染一個(gè)圖形一般是由三角形組成。

對(duì)于凸多邊形，分割三角形就比較簡(jiǎn)單。選取其中一個(gè)頂點(diǎn)，和其他頂點(diǎn)連接，就可以把多邊形分割成三角形。

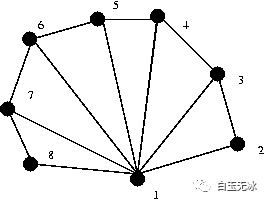
渲染一個(gè)凸多邊形采用Assembler的方式組裝頂點(diǎn)數(shù)據(jù)。

分為以下幾步實(shí)現(xiàn)：

1. 將引擎中的Sprite-simple組裝器拷貝出來(lái)，作為自己的組裝器模板。
2. 新建一個(gè)類繼承Sprite，并設(shè)置它的組裝器到自己的組裝器
3. 創(chuàng)建變量頂點(diǎn)數(shù)組，紋理數(shù)組。
4. 編寫(xiě)組裝器邏輯

直接看看代碼吧:D

凸多邊形的類。

// 僅限凸多邊形
@ccclass('PolygonSprite')
export class PolygonSprite extends Sprite {
    @property({ type: [Vec2] })
    protected _vertices: Vec2[] = [new Vec2(-100, -100), new Vec2(100, -100), new Vec2(100, 100), new Vec2(-100, 100)];
    // 省略部分代碼

    @property({ type: [Vec2] })
    protected _uvs: Vec2[] = [new Vec2(0, 0), new Vec2(1, 0), new Vec2(1, 1), new Vec2(0, 1)];
    // 省略部分代碼

    protected _flushAssembler() {
        //指向自定義的組裝器
        let assembler = polygonAssembler;
        if (this._assembler !== assembler) {
            this.destroyRenderData();
            this._assembler = assembler;
        }
        // 省略部分代碼
    }
}

接下來(lái)看組裝器內(nèi)修改部分。

處理頂點(diǎn)數(shù)據(jù)

// 保存頂點(diǎn)數(shù)據(jù)
updateVertexData(sprite: PolygonSprite) {
    //中間變量
    const renderData = sprite.renderData;
    if (!renderData) {
        return;
    }
    renderData.vertexCount = renderData.dataLength = sprite.vertices.length
    // 三角形數(shù)量 = 頂點(diǎn)數(shù) - 2
    // 索引數(shù)量 = 三角形數(shù)量X3
    renderData.indicesCount = (renderData.vertexCount - 2) * 3
    renderData.vertDirty = false;
    for (let i = 0; i < sprite.vertices.length; ++i) {
        const xy = sprite.vertices[i];
        renderData.data[i].x = xy.x
        renderData.data[i].y = xy.y
    }
},

緩存UV坐標(biāo)，我們定義的紋理坐標(biāo)是歸一化到0-1，在更新數(shù)據(jù)時(shí)再根據(jù)實(shí)際的紋理坐標(biāo)(合圖)進(jìn)行轉(zhuǎn)換。

updateUvs(sprite: PolygonSprite) {
    const renderData = sprite.renderData!;
    //實(shí)際uv
    const uv = sprite.spriteFrame!.uv;
    // 左 下 上 右 
    const l = uv[0], b = uv[1], t = uv[7], r = uv[6]
    for (let i = 0; i < sprite.uvs.length; ++i) {
        const uvs = sprite.uvs[i];
        renderData.data[i].u = l + (r - l) * uvs.x
        renderData.data[i].v = b + (t - b) * uvs.y
    }
    renderData.uvDirty = false;
},

填充數(shù)據(jù)修改，頂點(diǎn)索引就從第一個(gè)點(diǎn)開(kāi)始連接到各個(gè)頂點(diǎn)的三角形。

fillBuffers(sprite: PolygonSprite, renderer: any) {
    //省略代碼

    // 填充頂點(diǎn)
    for (let i = 0; i < renderData.vertexCount; ++i) {
        const vert = renderData.data[i];
        // 計(jì)算世界坐標(biāo)
        vBuf![vertexOffset++] = a * vert.x + c * vert.y + tx;
        vBuf![vertexOffset++] = b * vert.x + d * vert.y + ty;
        vBuf![vertexOffset++] = vert.z;
        // 填充uv
        vBuf![vertexOffset++] = vert.u;
        vBuf![vertexOffset++] = vert.v;
        Color.toArray(vBuf!, sprite.color, vertexOffset);
        vertexOffset += 4;
    }

    // 填充索引
    for (let i = 0; i < sprite.vertices.length - 2; ++i) {
        const start = i;
        iBuf![indicesOffset++] = vertexId;
        iBuf![indicesOffset++] = start + 1 + vertexId;
        iBuf![indicesOffset++] = start + 2 + vertexId;
    }
},

小結(jié)

實(shí)現(xiàn)折疊效果可以將問(wèn)題分解成處理一個(gè)多邊形的問(wèn)題，并用assembler實(shí)現(xiàn)合批渲染。

以上為白玉無(wú)冰使用 Cocos Creator 3.0.0 實(shí)現(xiàn) "折紙效果!" 的技術(shù)分享。歡迎三連(點(diǎn)贊/在看/留言/分享)支持!