?LeetCode刷題實(shí)戰(zhàn)47：全排列 II

樣例

輸入: [1,1,2]
輸出:
[
??[1,1,2],
??[1,2,1],
??[2,1,1]
]

解題

無腦解決

class?Solution:
????def?get_next(self,?nums:?List[int]):
????????"""
????????Do?not?return?anything,?modify?nums?in-place?instead.
????????"""
????????#?長度
????????n?=?len(nums)
????????#?記錄圖中i-1的位置
????????pos?=?n?-?1
????????for?i?in?range(n-1,?0,?-1):
????????????#?如果降序破壞，說明找到了i
????????????if?nums[i]?>?nums[i-1]:
????????????????pos?=?i-1
????????????????break
????????????????
????????for?i?in?range(n-1,?pos,?-1):
????????????#?從最后開始找大于pos位置的
????????????if?nums[i]?>?nums[pos]:
????????????????#?先交換元素，在進(jìn)行翻轉(zhuǎn)
????????????????nums[i],?nums[pos]?=?nums[pos],?nums[i]
????????????????#?翻轉(zhuǎn)[pos+1,?n]區(qū)間
????????????????nums[pos+1:]?=?nums[n:pos:-1]
????????????????return?False
????????return?True
????????
????????
????def?permuteUnique(self,?nums:?List[int])?->?List[List[int]]:
????????ret?=?[]
????????#?從小到大排序，獲得最小排列
????????nums?=?sorted(nums)
????????ret.append(nums.copy())
????????#?如果還有下一個(gè)排列則繼續(xù)調(diào)用
????????while?not?self.get_next(nums):
????????????#?要.copy()是因?yàn)镻ython中存儲的引用，如果不加copy
????????????#?會導(dǎo)致當(dāng)nums發(fā)生變化之后，ret中存儲的數(shù)據(jù)也會變化
????????????ret.append(nums.copy())
????????return?ret

回溯法

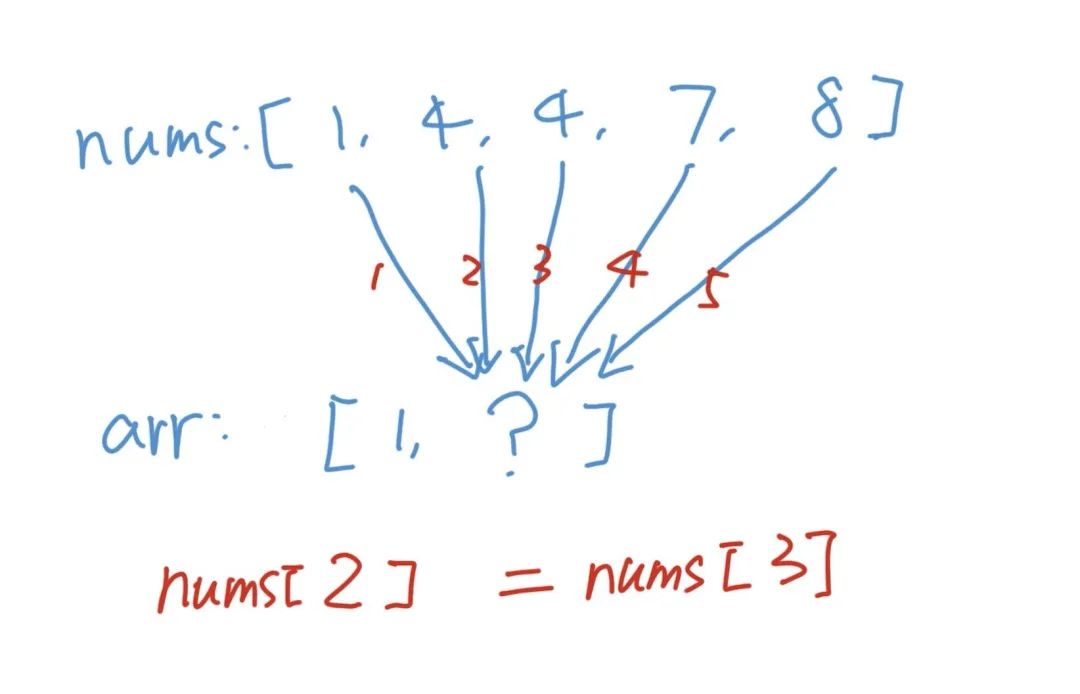
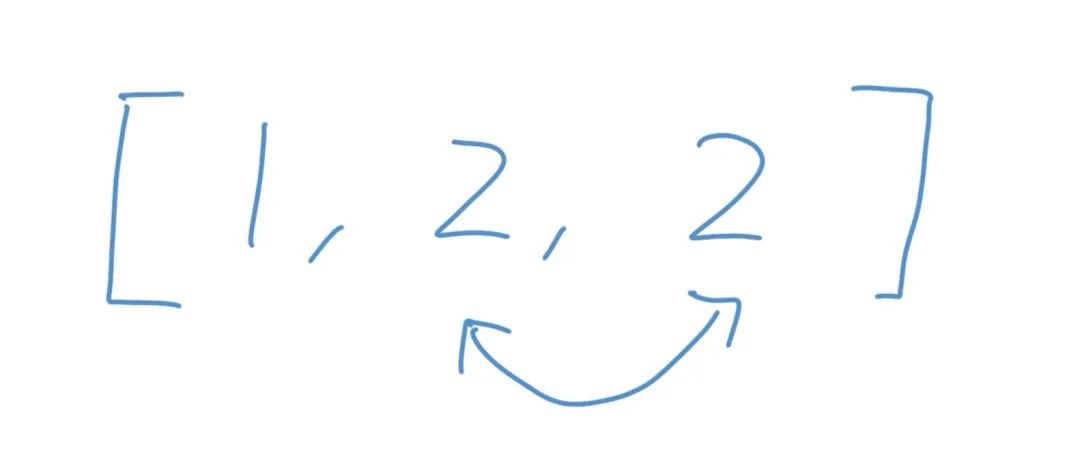
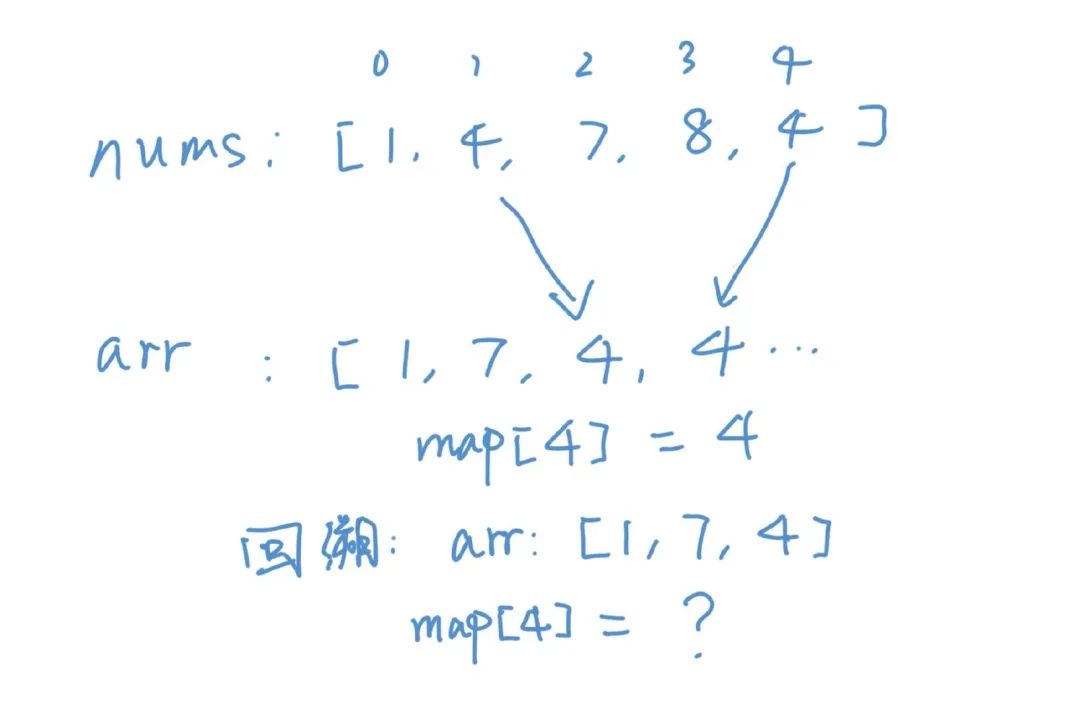
第二種情況也比較容易想明白，還是同樣的例子，我們給數(shù)組當(dāng)中的兩個(gè)4編號，一個(gè)編號是，一個(gè)是，我們會發(fā)現(xiàn)對于兩個(gè)位置，我們先放第一個(gè)再放第二個(gè)和先放第二個(gè)再放第一個(gè)是重復(fù)的。

class?Solution:
????def?dfs(self,?nums,?n,?i,?states,?cur,?ret,?flag):
????????if?i?==?n:
????????????ret.append(cur.copy())
????????????return
????????for?p?in?range(n):????????????????
????????????#?遍歷所有元素
????????????#?如果p元素已經(jīng)放置過了，或者是已經(jīng)放置了更后面的同元素
????????????#?跳過
????????????if?flag[p]?or?(nums[p]?in?states?and?states[nums[p]]?>=?p):
????????????????continue
????????????#?當(dāng)前位置放置p
????????????cur.append(nums[p])
????????????#?更新之前，記錄之前的值
????????????tmp,?states[nums[p]]?=?states[nums[p]]?if?nums[p]?in?states?else?-1,?p
????????????#?flag[p]置為True
????????????flag[p]?=?True
????????????#?遞歸
????????????self.dfs(nums,?n,?i+1,?states,?cur,?ret,?flag)
????????????#?回溯
????????????cur.pop()
????????????flag[p]?=?False
????????????#?恢復(fù)遞歸之前的值
????????????states[nums[p]]?=?tmp?
????????????#?states.remove((i,?nums[p]))
????????
????????
????def?permuteUnique(self,?nums:?List[int])?->?List[List[int]]:
????????ret?=?[]
????????n?=?len(nums)
????????#?記錄元素i有沒有放置過
????????flag?=?[False?for?_?in?range(n)]
????????self.dfs(nums,?n,?0,?{},?[],?ret,?flag)
????????return?ret

改進(jìn)

class?Solution:
????def?dfs(self,?nums,?n,?i,?cur,?ret,?flag):
????????if?i?==?n:
????????????ret.append(cur.copy())
????????????return
????????for?p?in?range(n):????????????????
????????????#?遍歷所有元素
????????????#?如果p元素已經(jīng)放置過了，或者
????????????#?如果nums[p-1]?==?nums[p]?并且flag[p-1]?是False
????????????#?跳過
????????????if?flag[p]?or?(p?>?0?and?nums[p-1]?==?nums[p]?and?not?flag[p-1]):
????????????????continue
????????????#?當(dāng)前位置放置p
????????????cur.append(nums[p])
????????????#?flag[p]置為True
????????????flag[p]?=?True
????????????#?遞歸
????????????self.dfs(nums,?n,?i+1,?cur,?ret,?flag)
????????????#?回溯
????????????cur.pop()
????????????flag[p]?=?False
????????
????????
????def?permuteUnique(self,?nums:?List[int])?->?List[List[int]]:
????????ret?=?[]
????????n?=?len(nums)
????????#?記錄元素i有沒有放置過
????????nums?=?sorted(nums)
????????flag?=?[False?for?_?in?range(n)]
????????self.dfs(nums,?n,?0,?[],?ret,?flag)
????????return?ret