基于 Python 的 Stacking 集成機器學習實踐

Stacking或Stacked Generalization是一種集成的機器學習算法。它使用元學習算法來學習如何最佳地組合來自兩個或多個基礎機器學習算法的預測。堆疊的好處在于，它可以利用分類或回歸任務上一系列性能良好的模型的功能，并做出比集合中的任何單個模型都有更好性能的預測。

在本教程中，您將發(fā)現(xiàn)堆疊的泛型集成或Python中的堆疊。完成本教程后，您將知道：

• 堆疊是一種集成的機器學習算法，可學習如何最佳地組合來自多個性能良好的機器學習模型的預測。
• scikit-learn庫提供了Python中堆棧集成的標準實現(xiàn)。
• 如何使用堆疊集成進行回歸和分類預測建模。

教程概述

本教程分為四個部分。他們是：

• 堆疊概括
• 堆疊Scikit-Learn API
• 堆疊分類
• 堆疊回歸

堆疊概括

堆疊通用化或簡稱“堆疊”是一種集成的機器學習算法。它涉及在同一數(shù)據(jù)集上組合來自多個機器學習模型的預測，例如裝袋和提升。堆疊解決了這個問題：給定多個熟練解決問題的機器學習模型，但是以不同的方式，您如何選擇要使用的模型（信任）？解決此問題的方法是使用另一個機器學習模型，該模型學習何時使用或信任集合中的每個模型。

• 與Bagging不同，在堆疊中，模型通常是不同的（例如，并非所有決策樹）并且適合于同一數(shù)據(jù)集（例如，而不是訓練數(shù)據(jù)集的樣本）。
• 與Boosting不同，在堆疊中，使用單個模型來學習如何最佳地組合來自貢獻模型的預測（例如，而不是校正先前模型的預測的一系列模型）。

堆棧模型的體系結構涉及兩個或多個基本模型（通常稱為0級模型）和一個將基本模型的預測結合在一起的元模型（稱為1級模型）。

• 0級模型（基本模型）：模型適合訓練數(shù)據(jù)，并會編譯其預測。
• 1級模型（元模型）：學習如何最好地組合基礎模型的預測的模型。

元模型是根據(jù)基本模型對樣本外數(shù)據(jù)所做的預測進行訓練的。也就是說，將不用于訓練基本模型的數(shù)據(jù)饋送到基本模型，進行預測，并且這些預測與預期輸出一起提供用于擬合元模型的訓練數(shù)據(jù)集的輸入和輸出對。來自基本模型的輸出（用作元模型的輸入）在回歸的情況下可以是真實值，而在概率分類的情況下，概率值，類似概率的值或類別標簽可以是真實值。為元模型準備訓練數(shù)據(jù)集的最常見方法是通過基本模型的k折交叉驗證，其中不合時宜的預測用作元模型訓練數(shù)據(jù)集的基礎。

元模型的訓練數(shù)據(jù)還可以包括基本模型的輸入，例如基本模型的輸入。訓練數(shù)據(jù)的輸入元素。這可以向元模型提供關于如何最佳地組合來自元模型的預測的附加上下文。一旦為元模型準備了訓練數(shù)據(jù)集，就可以在該數(shù)據(jù)集上單獨訓練元模型，并且可以在整個原始訓練數(shù)據(jù)集上訓練基本模型。

當多個不同的機器學習模型在數(shù)據(jù)集上具有技能但以不同的方式具有技能時，堆疊是合適的。另一種說法是，模型做出的預測或模型做出的預測中的誤差不相關或具有較低的相關性。基本模型通常是復雜而多樣的。因此，通常最好使用一系列關于如何解決預測建模任務的不同假設的模型，例如線性模型，決策樹，支持向量機，神經(jīng)網(wǎng)絡等。其他集成算法也可以用作基本模型，例如隨機森林。基本模型：使用各種模型，這些模型對預測任務有不同的假設。元模型通常很簡單，可以對基本模型做出的預測進行平滑的解釋。這樣，線性模型通常用作元模型，例如用于回歸任務的線性回歸（預測數(shù)值）和用于分類任務的邏輯回歸（預測類標簽）。盡管這很普遍，但這不是必需的。

• 回歸元模型：線性回歸。
• 分類元模型：邏輯回歸。

使用簡單的線性模型作為元模型通常會堆疊口語名稱“ blending”。與預測中一樣，是基礎模型所做的預測的加權平均或混合。超級學習者可以被認為是一種特殊的堆疊方式。堆棧旨在提高建模性能，盡管不能保證在所有情況下都能改進。實現(xiàn)性能上的改進取決于問題的復雜性，以及培訓數(shù)據(jù)是否足夠好地表示問題以及是否足夠復雜，以至于可以通過組合預測來學習更多。它還取決于基本模型的選擇以及它們在預測（或錯誤）方面是否足夠熟練和足夠不相關。如果基本模型的性能優(yōu)于或優(yōu)于堆疊集成，則應使用基本模型，因為它的復雜度較低（例如，描述，訓練和維護更簡單）。

堆疊Scikit-Learn API

堆疊可以從頭開始實現(xiàn)，盡管這對初學者可能具有挑戰(zhàn)性。scikit-learn Python機器學習庫提供了用于機器學習的堆棧實現(xiàn)。它在庫的0.22版和更高版本中可用。首先，通過運行以下腳本來確認您正在使用現(xiàn)代版本的庫：

#?check?scikit-learn?version
import?sklearn
print(sklearn.__version__)

運行腳本將打印您的scikit-learn版本。您的版本應該相同或更高。如果不是，則必須升級scikit-learn庫的版本。

0.22.1

堆棧是通過StackingRegressor和StackingClassifier類提供的。兩種模型以相同的方式操作并采用相同的參數(shù)。使用模型要求您指定一個估算器列表（0級模型）和一個最終估算器（1級或元模型）。級別0模型或基本模型的列表通過“ estimators”參數(shù)提供。這是一個Python列表，其中列表中的每個元素都是一個具有模型名稱和配置的模型實例的元組。例如，下面定義了兩個0級模型：

models?=?[('lr',LogisticRegression()),('svm',SVC())
stacking?=?StackingClassifier(estimators=models)

列表中的每個模型也可以是管道，包括在將模型擬合到訓練數(shù)據(jù)集之前模型所需的任何數(shù)據(jù)準備。例如：

models?=?[('lr',LogisticRegression()),('svm',make_pipeline(StandardScaler(),SVC()))
stacking?=?StackingClassifier(estimators=models)

通過“ final_estimator”參數(shù)提供1級模型或元模型。默認情況下，將其設置為用于回歸的LinearRegression和用于分類的LogisticRegression，并且這些是您可能不希望更改的明智的默認值。使用交叉驗證準備元模型的數(shù)據(jù)集。默認情況下，使用5折交叉驗證，盡管可以通過“ cv”自變量進行更改，并將其設置為數(shù)字（例如10折交叉驗證為10）或交叉驗證對象（例如StratifiedKFold） 。有時，如果為元模型準備的數(shù)據(jù)集還包含0級模型的輸入（例如， 輸入的訓練數(shù)據(jù)。這可以通過將“ passthrough”參數(shù)設置為True來實現(xiàn)，并且默認情況下未啟用。現(xiàn)在，我們已經(jīng)熟悉了scikit-learn中的stacking API，下面讓我們來看一些可行的示例。

堆疊分類

在本節(jié)中，我們將研究使用堆疊解決分類問題。首先，我們可以使用make_classification（）函數(shù)創(chuàng)建具有1,000個示例和20個輸入功能的綜合二進制分類問題。下面列出了完整的示例。

#?test?classification?dataset
from?sklearn.datasets?import?make_classification
#?define?dataset
X,?y?=?make_classification(n_samples=1000,?n_features=20,?n_informative=15,?n_redundant=5,?random_state=1)
#?summarize?the?dataset
print(X.shape,?y.shape)

運行示例將創(chuàng)建數(shù)據(jù)集并總結輸入和輸出組件的形狀。

(1000,?20)?(1000,)

接下來，我們可以在數(shù)據(jù)集上評估一套不同的機器學習模型。

具體來說，我們將評估以下五種算法：

• 邏輯回歸。
• k最近鄰居。
• 決策樹。
• 支持向量機。
• 天真貝葉斯。

每種算法將使用默認模型超參數(shù)進行評估。下面的函數(shù)get_models（）創(chuàng)建我們要評估的模型。

#?get?a?list?of?models?to?evaluate
def?get_models():
?models?=?dict()
?models['lr']?=?LogisticRegression()
?models['knn']?=?KNeighborsClassifier()
?models['cart']?=?DecisionTreeClassifier()
?models['svm']?=?SVC()
?models['bayes']?=?GaussianNB()
?return?models

每個模型將使用重復的k倍交叉驗證進行評估。下面的valuate_model（）函數(shù)采用一個模型實例，并從分層的10倍交叉驗證的三個重復中返回分數(shù)列表。

#?evaluate?a?given?model?using?cross-validation
def?evaluate_model(model,?X,?y):
?cv?=?RepeatedStratifiedKFold(n_splits=10,?n_repeats=3,?random_state=1)
?scores?=?cross_val_score(model,?X,?y,?scoring='accuracy',?cv=cv,?n_jobs=-1,?error_score='raise')
?return?scores

然后，我們可以報告每種算法的平均性能，還可以創(chuàng)建箱形圖和晶須圖，以比較每種算法的準確性得分的分布。結合在一起，下面列出了完整的示例。

#?compare?standalone?models?for?binary?classification
from?numpy?import?mean
from?numpy?import?std
from?sklearn.datasets?import?make_classification
from?sklearn.model_selection?import?cross_val_score
from?sklearn.model_selection?import?RepeatedStratifiedKFold
from?sklearn.linear_model?import?LogisticRegression
from?sklearn.neighbors?import?KNeighborsClassifier
from?sklearn.tree?import?DecisionTreeClassifier
from?sklearn.svm?import?SVC
from?sklearn.naive_bayes?import?GaussianNB
from?matplotlib?import?pyplot
?
#?get?the?dataset
def?get_dataset():
?X,?y?=?make_classification(n_samples=1000,?n_features=20,?n_informative=15,?n_redundant=5,?random_state=1)
?return?X,?y
?
#?get?a?list?of?models?to?evaluate
def?get_models():
?models?=?dict()
?models['lr']?=?LogisticRegression()
?models['knn']?=?KNeighborsClassifier()
?models['cart']?=?DecisionTreeClassifier()
?models['svm']?=?SVC()
?models['bayes']?=?GaussianNB()
?return?models
?
#?evaluate?a?given?model?using?cross-validation
def?evaluate_model(model,?X,?y):
?cv?=?RepeatedStratifiedKFold(n_splits=10,?n_repeats=3,?random_state=1)
?scores?=?cross_val_score(model,?X,?y,?scoring='accuracy',?cv=cv,?n_jobs=-1,?error_score='raise')
?return?scores
?
#?define?dataset
X,?y?=?get_dataset()
#?get?the?models?to?evaluate
models?=?get_models()
#?evaluate?the?models?and?store?results
results,?names?=?list(),?list()
for?name,?model?in?models.items():
?scores?=?evaluate_model(model,?X,?y)
?results.append(scores)
?names.append(name)
?print('>%s?%.3f?(%.3f)'?%?(name,?mean(scores),?std(scores)))
#?plot?model?performance?for?comparison
pyplot.boxplot(results,?labels=names,?showmeans=True)
pyplot.show()

首先運行示例將報告每個模型的均值和標準差準確性。注意：由于算法或評估程序的隨機性，或者數(shù)值精度的差異，您的結果可能會有所不同。考慮運行該示例幾次并比較平均結果。我們可以看到，在這種情況下，SVM以約95.7％的平均準確度表現(xiàn)最佳。

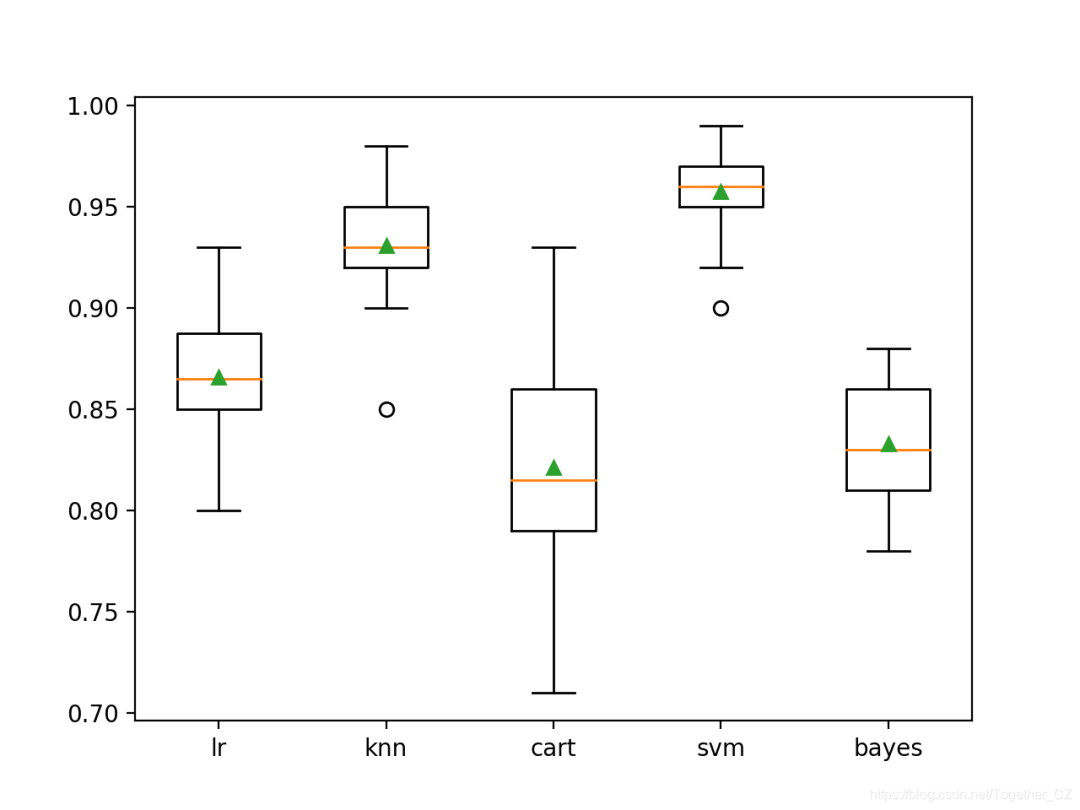
>lr?0.866?(0.029)
>knn?0.931?(0.025)
>cart?0.821?(0.050)
>svm?0.957?(0.020)
>bayes?0.833?(0.031)

首先運行示例將報告每個模型的均值和標準差準確性。注意：由于算法或評估程序的隨機性，或者數(shù)值精度的差異，您的結果可能會有所不同。考慮運行該示例幾次并比較平均結果。我們可以看到，在這種情況下，SVM以約95.7％的平均準確度表現(xiàn)最佳。

在這里，我們有五種不同的算法運行良好，大概在此數(shù)據(jù)集上的表現(xiàn)方式不同。接下來，我們可以嘗試使用堆棧將這五個模型合并為一個整體模型。我們可以使用邏輯回歸模型來學習如何最好地結合來自五個單獨模型的預測。下面的get_stacking（）函數(shù)通過首先為五個基本模型定義一個元組列表，然后定義邏輯回歸元模型以使用5倍交叉驗證組合來自基本模型的預測來定義StackingClassifier模型。

#?get?a?stacking?ensemble?of?models
def?get_stacking():
?#?define?the?base?models
?level0?=?list()
?level0.append(('lr',?LogisticRegression()))
?level0.append(('knn',?KNeighborsClassifier()))
?level0.append(('cart',?DecisionTreeClassifier()))
?level0.append(('svm',?SVC()))
?level0.append(('bayes',?GaussianNB()))
?#?define?meta?learner?model
?level1?=?LogisticRegression()
?#?define?the?stacking?ensemble
?model?=?StackingClassifier(estimators=level0,?final_estimator=level1,?cv=5)
?return?model

我們可以將堆棧集成與獨立模型一起包括在要評估的模型列表中。

#?get?a?list?of?models?to?evaluate
def?get_models():
?models?=?dict()
?models['lr']?=?LogisticRegression()
?models['knn']?=?KNeighborsClassifier()
?models['cart']?=?DecisionTreeClassifier()
?models['svm']?=?SVC()
?models['bayes']?=?GaussianNB()
?models['stacking']?=?get_stacking()
?return?models

我們的期望是，堆疊集成的性能將優(yōu)于任何單個基本模型。并非總是如此，如果不是這種情況，則應使用基礎模型，以支持集成模型。下面列出了評估堆疊集成模型和獨立模型的完整示例。

#?compare?ensemble?to?each?baseline?classifier
from?numpy?import?mean
from?numpy?import?std
from?sklearn.datasets?import?make_classification
from?sklearn.model_selection?import?cross_val_score
from?sklearn.model_selection?import?RepeatedStratifiedKFold
from?sklearn.linear_model?import?LogisticRegression
from?sklearn.neighbors?import?KNeighborsClassifier
from?sklearn.tree?import?DecisionTreeClassifier
from?sklearn.svm?import?SVC
from?sklearn.naive_bayes?import?GaussianNB
from?sklearn.ensemble?import?StackingClassifier
from?matplotlib?import?pyplot
?
#?get?the?dataset
def?get_dataset():
?X,?y?=?make_classification(n_samples=1000,?n_features=20,?n_informative=15,?n_redundant=5,?random_state=1)
?return?X,?y
?
#?get?a?stacking?ensemble?of?models
def?get_stacking():
?#?define?the?base?models
?level0?=?list()
?level0.append(('lr',?LogisticRegression()))
?level0.append(('knn',?KNeighborsClassifier()))
?level0.append(('cart',?DecisionTreeClassifier()))
?level0.append(('svm',?SVC()))
?level0.append(('bayes',?GaussianNB()))
?#?define?meta?learner?model
?level1?=?LogisticRegression()
?#?define?the?stacking?ensemble
?model?=?StackingClassifier(estimators=level0,?final_estimator=level1,?cv=5)
?return?model
?
#?get?a?list?of?models?to?evaluate
def?get_models():
?models?=?dict()
?models['lr']?=?LogisticRegression()
?models['knn']?=?KNeighborsClassifier()
?models['cart']?=?DecisionTreeClassifier()
?models['svm']?=?SVC()
?models['bayes']?=?GaussianNB()
?models['stacking']?=?get_stacking()
?return?models
?
#?evaluate?a?give?model?using?cross-validation
def?evaluate_model(model,?X,?y):
?cv?=?RepeatedStratifiedKFold(n_splits=10,?n_repeats=3,?random_state=1)
?scores?=?cross_val_score(model,?X,?y,?scoring='accuracy',?cv=cv,?n_jobs=-1,?error_score='raise')
?return?scores
?
#?define?dataset
X,?y?=?get_dataset()
#?get?the?models?to?evaluate
models?=?get_models()
#?evaluate?the?models?and?store?results
results,?names?=?list(),?list()
for?name,?model?in?models.items():
?scores?=?evaluate_model(model,?X,?y)
?results.append(scores)
?names.append(name)
?print('>%s?%.3f?(%.3f)'?%?(name,?mean(scores),?std(scores)))
#?plot?model?performance?for?comparison
pyplot.boxplot(results,?labels=names,?showmeans=True)
pyplot.show()

首先運行示例將報告每個模型的性能。這包括每個基本模型的性能，然后是堆疊合奏。

注意：由于算法或評估程序的隨機性，或者數(shù)值精度的差異，您的結果可能會有所不同。考慮運行該示例幾次并比較平均結果。在這種情況下，我們可以看到堆疊集成的平均性能似乎比任何單個模型都要好，達到了約96.4％的精度。

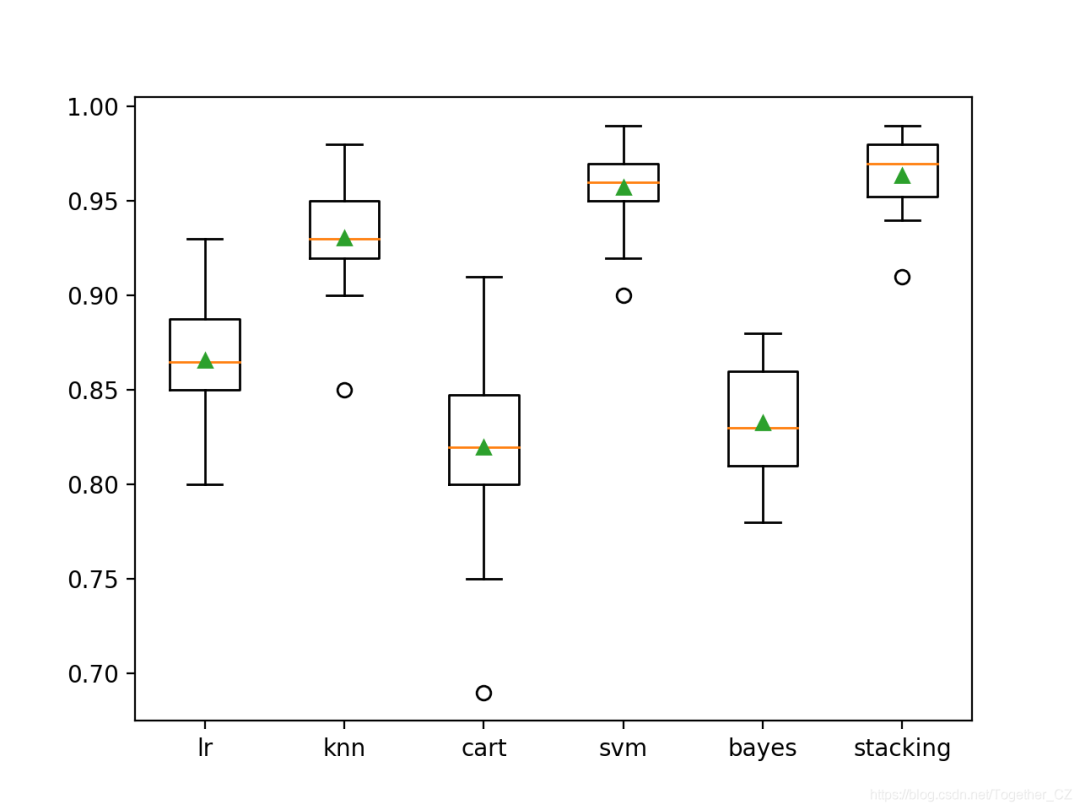
>lr?0.866?(0.029)
>knn?0.931?(0.025)
>cart?0.820?(0.044)
>svm?0.957?(0.020)
>bayes?0.833?(0.031)
>stacking?0.964?(0.019)

將創(chuàng)建一個箱形圖，以顯示模型分類精度的分布。在這里，我們可以看到堆疊模型的均值和中值準確性比SVM模型要高一些。

如果我們選擇堆疊集成作為最終模型，則可以像其他任何模型一樣擬合并使用它對新數(shù)據(jù)進行預測。首先，將堆棧集合適合所有可用數(shù)據(jù)，然后可以調用predict（）函數(shù)對新數(shù)據(jù)進行預測。下面的示例在我們的二進制分類數(shù)據(jù)集中展示了這一點。

#?make?a?prediction?with?a?stacking?ensemble
from?sklearn.datasets?import?make_classification
from?sklearn.ensemble?import?StackingClassifier
from?sklearn.linear_model?import?LogisticRegression
from?sklearn.neighbors?import?KNeighborsClassifier
from?sklearn.tree?import?DecisionTreeClassifier
from?sklearn.svm?import?SVC
from?sklearn.naive_bayes?import?GaussianNB
#?define?dataset
X,?y?=?make_classification(n_samples=1000,?n_features=20,?n_informative=15,?n_redundant=5,?random_state=1)
#?define?the?base?models
level0?=?list()
level0.append(('lr',?LogisticRegression()))
level0.append(('knn',?KNeighborsClassifier()))
level0.append(('cart',?DecisionTreeClassifier()))
level0.append(('svm',?SVC()))
level0.append(('bayes',?GaussianNB()))
#?define?meta?learner?model
level1?=?LogisticRegression()
#?define?the?stacking?ensemble
model?=?StackingClassifier(estimators=level0,?final_estimator=level1,?cv=5)
#?fit?the?model?on?all?available?data
model.fit(X,?y)
#?make?a?prediction?for?one?example
data?=?[[2.47475454,0.40165523,1.68081787,2.88940715,0.91704519,-3.07950644,4.39961206,0.72464273,-4.86563631,-6.06338084,-1.22209949,-0.4699618,1.01222748,-0.6899355,-0.53000581,6.86966784,-3.27211075,-6.59044146,-2.21290585,-3.139579]]
yhat?=?model.predict(data)
print('Predicted?Class:?%d'?%?(yhat))

運行示例適合整個數(shù)據(jù)集上的堆疊集成模型，然后像在應用程序中使用模型一樣，將其用于對新數(shù)據(jù)行進行預測。

Predicted?Class:?0

堆疊回歸

在本節(jié)中，我們將研究如何使用堆疊來解決回歸問題。首先，我們可以使用make_regression（）函數(shù)創(chuàng)建具有1000個示例和20個輸入要素的綜合回歸問題。下面列出了完整的示例。

#?test?regression?dataset
from?sklearn.datasets?import?make_regression
#?define?dataset
X,?y?=?make_regression(n_samples=1000,?n_features=20,?n_informative=15,?noise=0.1,?random_state=1)
#?summarize?the?dataset
print(X.shape,?y.shape)

運行示例將創(chuàng)建數(shù)據(jù)集并總結輸入和輸出組件的形狀。

(1000,?20)?(1000,)

接下來，我們可以在數(shù)據(jù)集上評估一套不同的機器學習模型。

具體來說，我們將評估以下三種算法：

• k近鄰
• 決策樹
• 支持向量回歸

注意：可以使用線性回歸模型對測試數(shù)據(jù)集進行簡單求解，因為該數(shù)據(jù)集是在封面下使用線性模型創(chuàng)建的。因此，我們將把該模型放在示例之外，以便我們可以證明堆疊集成方法的好處。

每種算法將使用默認的模型超參數(shù)進行評估。下面的函數(shù)get_models（）創(chuàng)建我們要評估的模型。

#?get?a?list?of?models?to?evaluate
def?get_models():
?models?=?dict()
?models['knn']?=?KNeighborsRegressor()
?models['cart']?=?DecisionTreeRegressor()
?models['svm']?=?SVR()
?return?models

每個模型將使用重復的k倍交叉驗證進行評估。下面的valuate_model（）函數(shù)采用一個模型實例，并從三個重復的10倍交叉驗證中返回分數(shù)列表。

#?evaluate?a?given?model?using?cross-validation
def?evaluate_model(model,?X,?y):
?cv?=?RepeatedKFold(n_splits=10,?n_repeats=3,?random_state=1)
?scores?=?cross_val_score(model,?X,?y,?scoring='neg_mean_absolute_error',?cv=cv,?n_jobs=-1,?error_score='raise')
?return?scores

然后，我們可以報告每種算法的平均性能，還可以創(chuàng)建箱形圖和晶須圖，以比較每種算法的準確性得分的分布。在這種情況下，將使用平均絕對誤差（MAE）報告模型性能。scikit-learn庫會將此錯誤的符號反轉以使其最大化，從-infinity到0以獲取最佳分數(shù)。結合在一起，下面列出了完整的示例。

#?compare?machine?learning?models?for?regression
from?numpy?import?mean
from?numpy?import?std
from?sklearn.datasets?import?make_regression
from?sklearn.model_selection?import?cross_val_score
from?sklearn.model_selection?import?RepeatedKFold
from?sklearn.linear_model?import?LinearRegression
from?sklearn.neighbors?import?KNeighborsRegressor
from?sklearn.tree?import?DecisionTreeRegressor
from?sklearn.svm?import?SVR
from?matplotlib?import?pyplot
?
#?get?the?dataset
def?get_dataset():
?X,?y?=?make_regression(n_samples=1000,?n_features=20,?n_informative=15,?noise=0.1,?random_state=1)
?return?X,?y
?
#?get?a?list?of?models?to?evaluate
def?get_models():
?models?=?dict()
?models['knn']?=?KNeighborsRegressor()
?models['cart']?=?DecisionTreeRegressor()
?models['svm']?=?SVR()
?return?models
?
#?evaluate?a?given?model?using?cross-validation
def?evaluate_model(model,?X,?y):
?cv?=?RepeatedKFold(n_splits=10,?n_repeats=3,?random_state=1)
?scores?=?cross_val_score(model,?X,?y,?scoring='neg_mean_absolute_error',?cv=cv,?n_jobs=-1,?error_score='raise')
?return?scores
?
#?define?dataset
X,?y?=?get_dataset()
#?get?the?models?to?evaluate
models?=?get_models()
#?evaluate?the?models?and?store?results
results,?names?=?list(),?list()
for?name,?model?in?models.items():
?scores?=?evaluate_model(model,?X,?y)
?results.append(scores)
?names.append(name)
?print('>%s?%.3f?(%.3f)'?%?(name,?mean(scores),?std(scores)))
#?plot?model?performance?for?comparison
pyplot.boxplot(results,?labels=names,?showmeans=True)
pyplot.show()

首先運行示例，報告每個模型的均值和標準差MAE。注意：由于算法或評估程序的隨機性，或者數(shù)值精度的差異，您的結果可能會有所不同。考慮運行該示例幾次并比較平均結果。我們可以看到，在這種情況下，KNN的最佳表現(xiàn)為平均負MAE約為-100。

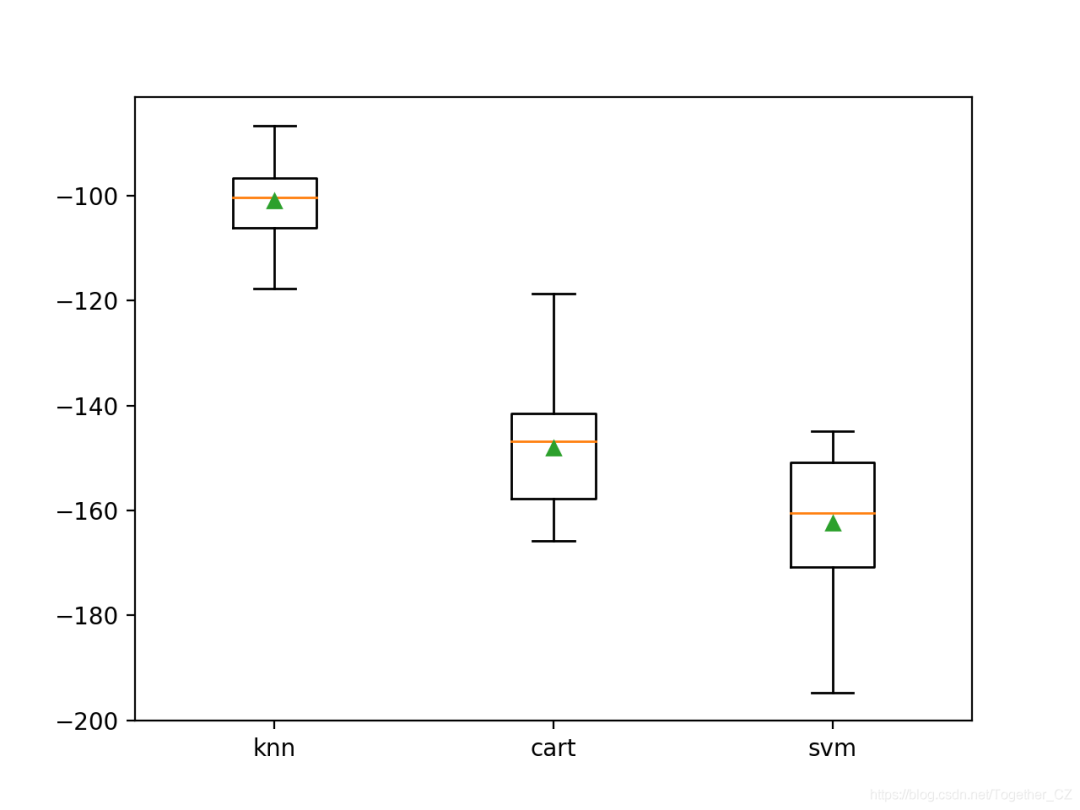
>knn?-101.019?(7.161)
>cart?-148.100?(11.039)
>svm?-162.419?(12.565)

然后創(chuàng)建箱型圖，比較每個模型的分布負MAE得分。

在這里，我們有三種不同的算法可以很好地運行，大概在此數(shù)據(jù)集上以不同的方式運行。

接下來，我們可以嘗試使用堆棧將這三個模型合并為一個整體模型。

我們可以使用線性回歸模型來學習如何最佳地組合來自三個模型的預測。

下面的get_stacking（）函數(shù)通過首先為三個基本模型定義一個元組列表，然后定義線性回歸元模型以使用5倍交叉驗證組合來自基本模型的預測來定義StackingRegressor模型。

#?get?a?stacking?ensemble?of?models
def?get_stacking():
?#?define?the?base?models
?level0?=?list()
?level0.append(('knn',?KNeighborsRegressor()))
?level0.append(('cart',?DecisionTreeRegressor()))
?level0.append(('svm',?SVR()))
?#?define?meta?learner?model
?level1?=?LinearRegression()
?#?define?the?stacking?ensemble
?model?=?StackingRegressor(estimators=level0,?final_estimator=level1,?cv=5)
?return?model

我們可以將堆棧集成與獨立模型一起包括在要評估的模型列表中

#?get?a?list?of?models?to?evaluate
def?get_models():
?models?=?dict()
?models['knn']?=?KNeighborsRegressor()
?models['cart']?=?DecisionTreeRegressor()
?models['svm']?=?SVR()
?models['stacking']?=?get_stacking()
?return?models

我們的期望是，堆疊集成的性能將優(yōu)于任何單個基本模型。情況并非總是如此，如果不是這種情況，則應使用基礎模型以支持集成模型。下面列出了評估堆疊集成模型和獨立模型的完整示例。

#?compare?ensemble?to?each?standalone?models?for?regression
from?numpy?import?mean
from?numpy?import?std
from?sklearn.datasets?import?make_regression
from?sklearn.model_selection?import?cross_val_score
from?sklearn.model_selection?import?RepeatedKFold
from?sklearn.linear_model?import?LinearRegression
from?sklearn.neighbors?import?KNeighborsRegressor
from?sklearn.tree?import?DecisionTreeRegressor
from?sklearn.svm?import?SVR
from?sklearn.ensemble?import?StackingRegressor
from?matplotlib?import?pyplot
?
#?get?the?dataset
def?get_dataset():
?X,?y?=?make_regression(n_samples=1000,?n_features=20,?n_informative=15,?noise=0.1,?random_state=1)
?return?X,?y
?
#?get?a?stacking?ensemble?of?models
def?get_stacking():
?#?define?the?base?models
?level0?=?list()
?level0.append(('knn',?KNeighborsRegressor()))
?level0.append(('cart',?DecisionTreeRegressor()))
?level0.append(('svm',?SVR()))
?#?define?meta?learner?model
?level1?=?LinearRegression()
?#?define?the?stacking?ensemble
?model?=?StackingRegressor(estimators=level0,?final_estimator=level1,?cv=5)
?return?model
?
#?get?a?list?of?models?to?evaluate
def?get_models():
?models?=?dict()
?models['knn']?=?KNeighborsRegressor()
?models['cart']?=?DecisionTreeRegressor()
?models['svm']?=?SVR()
?models['stacking']?=?get_stacking()
?return?models
?
#?evaluate?a?given?model?using?cross-validation
def?evaluate_model(model,?X,?y):
?cv?=?RepeatedKFold(n_splits=10,?n_repeats=3,?random_state=1)
?scores?=?cross_val_score(model,?X,?y,?scoring='neg_mean_absolute_error',?cv=cv,?n_jobs=-1,?error_score='raise')
?return?scores
?
#?define?dataset
X,?y?=?get_dataset()
#?get?the?models?to?evaluate
models?=?get_models()
#?evaluate?the?models?and?store?results
results,?names?=?list(),?list()
for?name,?model?in?models.items():
?scores?=?evaluate_model(model,?X,?y)
?results.append(scores)
?names.append(name)
?print('>%s?%.3f?(%.3f)'?%?(name,?mean(scores),?std(scores)))
#?plot?model?performance?for?comparison
pyplot.boxplot(results,?labels=names,?showmeans=True)
pyplot.show()

首先運行示例將報告每個模型的性能。這包括每個基本模型的性能，然后是堆疊合奏。注意：由于算法或評估程序的隨機性，或者數(shù)值精度的差異，您的結果可能會有所不同。考慮運行該示例幾次并比較平均結果。在這種情況下，我們可以看到堆疊集成的平均表現(xiàn)要好于任何單個模型，平均負MAE約為-56。

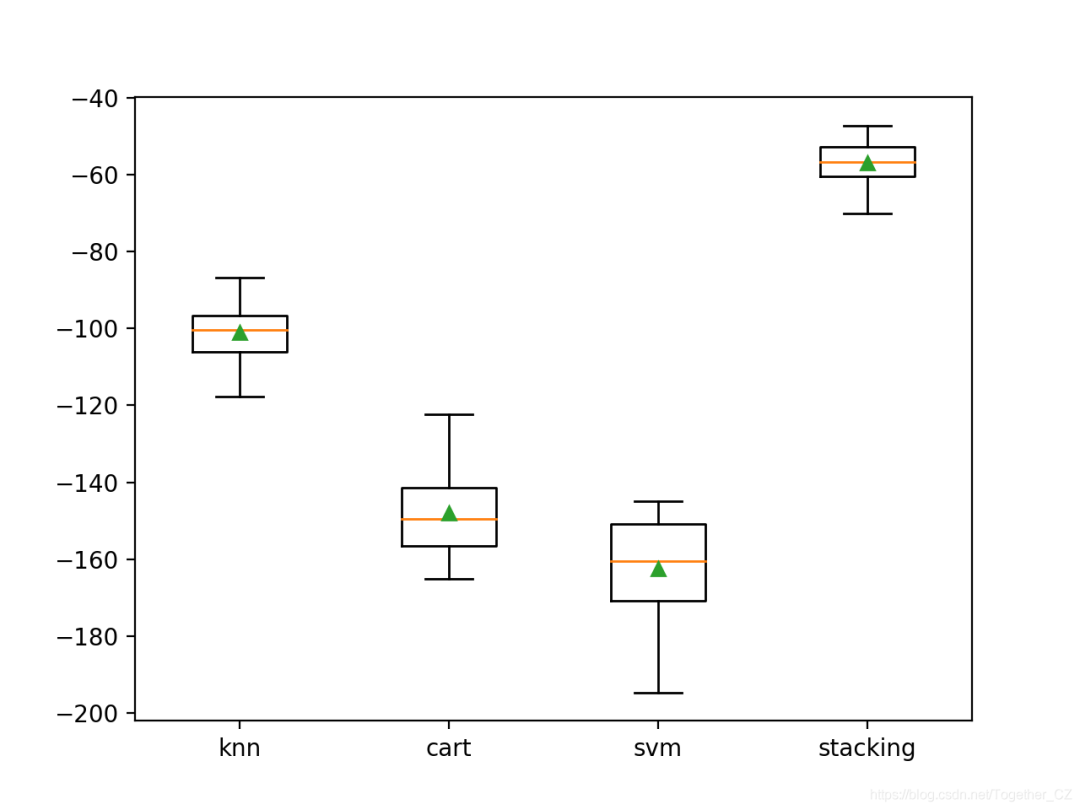
>knn?-101.019?(7.161)
>cart?-148.017?(10.635)
>svm?-162.419?(12.565)
>stacking?-56.893?(5.253)

將創(chuàng)建一個箱形圖，以顯示模型錯誤分數(shù)的分布。在這里，我們可以看到堆疊模型的平均得分和中位數(shù)得分遠高于任何單個模型。

如果我們選擇堆疊集成作為最終模型，則可以像其他任何模型一樣擬合并使用它對新數(shù)據(jù)進行預測。首先，將堆棧集合適合所有可用數(shù)據(jù)，然后可以調用predict（）函數(shù)對新數(shù)據(jù)進行預測。下面的示例在我們的回歸數(shù)據(jù)集中展示了這一點。

#?make?a?prediction?with?a?stacking?ensemble
from?sklearn.datasets?import?make_regression
from?sklearn.linear_model?import?LinearRegression
from?sklearn.neighbors?import?KNeighborsRegressor
from?sklearn.tree?import?DecisionTreeRegressor
from?sklearn.svm?import?SVR
from?sklearn.ensemble?import?StackingRegressor
#?define?dataset
X,?y?=?make_regression(n_samples=1000,?n_features=20,?n_informative=15,?noise=0.1,?random_state=1)
#?define?the?base?models
level0?=?list()
level0.append(('knn',?KNeighborsRegressor()))
level0.append(('cart',?DecisionTreeRegressor()))
level0.append(('svm',?SVR()))
#?define?meta?learner?model
level1?=?LinearRegression()
#?define?the?stacking?ensemble
model?=?StackingRegressor(estimators=level0,?final_estimator=level1,?cv=5)
#?fit?the?model?on?all?available?data
model.fit(X,?y)
#?make?a?prediction?for?one?example
data?=?[[0.59332206,-0.56637507,1.34808718,-0.57054047,-0.72480487,1.05648449,0.77744852,0.07361796,0.88398267,2.02843157,1.01902732,0.11227799,0.94218853,0.26741783,0.91458143,-0.72759572,1.08842814,-0.61450942,-0.69387293,1.69169009]]
yhat?=?model.predict(data)
print('Predicted?Value:?%.3f'?%?(yhat))

運行示例適合整個數(shù)據(jù)集上的堆疊集成模型，然后像在應用程序中使用模型一樣，將其用于對新數(shù)據(jù)行進行預測。

Predicted?Value:?556.264

作者：沂水寒城，CSDN博客專家，個人研究方向：機器學習、深度學習、NLP、CV

Blog:?http://yishuihancheng.blog.csdn.net

贊 賞 作 者

更多閱讀

[視頻]GitHub趨勢榜（2021年1月上旬）

特別推薦

點擊下方閱讀原文加入社區(qū)會員