干貨|變鄰域搜索(VNS)算法求解Max-Mean Dispersion Problem(附...
Part
1
Max-Mean?Dispersion Problem

對(duì)MDP和MMDP還是一頭霧水?不要著急,今天就和小編一起解決這三個(gè)問(wèn)題—
什么是MDP和MMDP?
它們有什么用?
怎樣解決這兩個(gè)問(wèn)題?
1.1
Maximum Diversity Problem
要討論Max-Mean Dispersion Problem,就要首先了解Maximum Diversity Problem (MDP)?。
MDP是一種用來(lái)度量元素中差異的問(wèn)題,通俗來(lái)講,就是要從一個(gè)集合中選擇一個(gè)子集合,使得子集合中的元素差異最大化。
舉個(gè)例子,對(duì)于生態(tài)系統(tǒng)的平衡問(wèn)題,生態(tài)系統(tǒng)的存續(xù)與否就在于多樣性。假如我們擁有任意兩個(gè)生物之間的差異值,通過(guò)找到具有最大多樣性的子集,我們就能方便地建立起可行的生態(tài)系統(tǒng)。
又比如說(shuō)在農(nóng)業(yè)育種中,往往需要在子代中挑選出具有理想多樣性的種群,問(wèn)題就又歸結(jié)到了在子代中找到最大差異化個(gè)體的問(wèn)題上了。
文章開(kāi)頭的表情包,其實(shí)質(zhì)也是一個(gè)MDP。在風(fēng)險(xiǎn)投資中,往往要通過(guò)找到差異最大的幾個(gè)市場(chǎng)來(lái)進(jìn)行投資,避免牽一發(fā)而動(dòng)全身的情況。
例子都是多樣性在生活中發(fā)揮作用的表現(xiàn),那么我們應(yīng)該如何最大化這種多樣性呢?這就是MDP要解決的問(wèn)題了。
更多的應(yīng)用見(jiàn)下圖:

1.2
MDP的數(shù)學(xué)描述
考慮一個(gè)元素的集合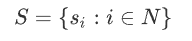 ,索引集
,索引集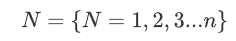 。每個(gè)元素包含著r個(gè)屬性,我們可以將一個(gè)元素用向量
。每個(gè)元素包含著r個(gè)屬性,我們可以將一個(gè)元素用向量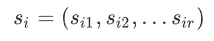 表示。我們的目標(biāo)就是從n個(gè)元素中選擇m個(gè)元素,最大化所選擇的元素的多樣性。為了度量元素之間的多樣性,我們定義值
表示。我們的目標(biāo)就是從n個(gè)元素中選擇m個(gè)元素,最大化所選擇的元素的多樣性。為了度量元素之間的多樣性,我們定義值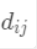 來(lái)代表元素i,j之間的距離。這個(gè)距離有多種算法,如歐幾里得距離,曼哈頓距離等。在這里我們使用最為常用的歐幾里得距離。
來(lái)代表元素i,j之間的距離。這個(gè)距離有多種算法,如歐幾里得距離,曼哈頓距離等。在這里我們使用最為常用的歐幾里得距離。? ? ? ? ? ?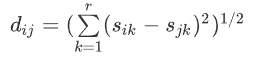
由此,我們可以定義一組元素的多樣性為:
???? ? ??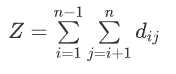
根據(jù)這些約定,我們可以通過(guò)引入0-1變量的方法,將問(wèn)題表達(dá)為:
? ??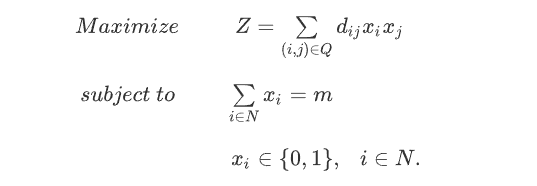
1.3
Max-Mean Dispersion Problem
有了對(duì)MDP問(wèn)題的認(rèn)識(shí),下面我們來(lái)看看MMDP。
和MDP要最大化子集的多樣性不同,MMDP問(wèn)題需要最大化子集多樣性的平均值。在這里值得注意的一點(diǎn)是,MDP中子集的大小是固定的,是問(wèn)題給出的。而MMDP中,子集數(shù)量的多少需要自己確定。當(dāng)子集數(shù)量確定后,MMDP就轉(zhuǎn)化為了MDP。
還是有些云里霧里?更通俗的講,假如說(shuō)問(wèn)題是在10個(gè)人中挑出差異最大的5個(gè)人,這自然是一個(gè)MDP,但假如說(shuō)問(wèn)題是在10個(gè)人中挑出幾個(gè)人,使這幾個(gè)人的差異最大呢?這時(shí)自然不能考慮差異值的和,而是需要考慮差異值的和的平均值,即MMDP了。
我們用一個(gè)簡(jiǎn)單的例子來(lái)具體解釋MDP和MMDP:
假設(shè)給出4個(gè)元素A,B,C,D,給出4個(gè)元素的距離矩陣如下圖:
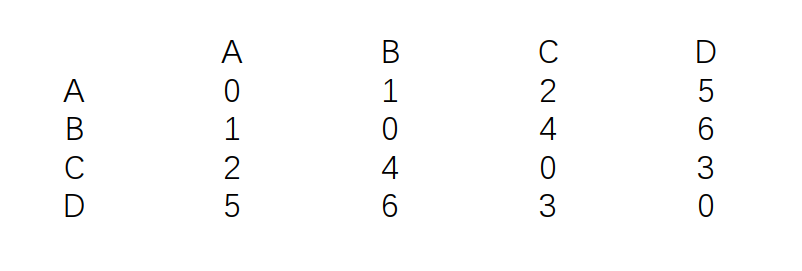
假如要求是從4個(gè)元素中選擇3個(gè)元素,使它們之間的差異最大,這就是一個(gè)MDP。假設(shè)選擇元素A,B,C,則目標(biāo)函數(shù)的值為1+2+4 = 7.
假如要求是從4個(gè)元素中選擇任意個(gè)元素,使他們之間的平均差異最大,這就是一個(gè)MMDP。同樣假設(shè)選擇元素A,B,C,目標(biāo)函數(shù)的值就變?yōu)椋?+2+4)/ 3 = 7/3。
Part
2
變鄰域搜索(VNS)算法再回顧
在之前的推文干貨 | 變鄰域搜索算法(Variable Neighborhood Search,VNS)超詳細(xì)一看就懂中,已經(jīng)對(duì)VNS算法有了詳細(xì)的介紹。
在干貨 | 變鄰域搜索算法(VNS)求解TSP(附C++詳細(xì)代碼及注釋)
中,給出了VNS算法解決問(wèn)題的實(shí)例。
在這里,我們簡(jiǎn)要地復(fù)習(xí)下VNS算法的基本內(nèi)容,詳細(xì)內(nèi)容參見(jiàn)以上推文。
2.1
VNS算法介紹
VNS算法的基本思想是在搜索過(guò)程中系統(tǒng)地改變鄰域結(jié)構(gòu)集來(lái)拓展搜索過(guò)程,獲得局部最優(yōu)解,再基于此局部最優(yōu)解重新系統(tǒng)地改變鄰域結(jié)構(gòu)集拓展搜索范圍找到另一個(gè)局部最優(yōu)解的過(guò)程。基本的流程如下圖:

正如Hansen在論文Variable neighborhood search Principles and applications一文中提到的,VNS算法本質(zhì)上還是一種跳出局部最優(yōu)解的算法。和禁忌搜索與模擬退火算法不同,其算法并不遵循一定的"軌跡",而是通過(guò)shaking動(dòng)作來(lái)跳出當(dāng)前局部最優(yōu)解,在不同的鄰域中找到其他局部最優(yōu)解,當(dāng)且僅當(dāng)該解優(yōu)于當(dāng)前解時(shí)進(jìn)行移動(dòng)。假如鄰域結(jié)構(gòu)可以覆蓋整個(gè)可行解集,則算法可以找到全局最優(yōu)解。
Part
3
具體算法介紹
3.1
初始解生成
對(duì)于初始解,我們使用貪心的方法來(lái)構(gòu)造。最開(kāi)始將所有元素都視為已選擇,計(jì)算出每一元素被移除后,該解目標(biāo)函數(shù)值的提高,不斷地移除能提高最多的元素,不斷循環(huán),直到不再有元素被移除時(shí)目標(biāo)函數(shù)值提高為止。
3.2
鄰域動(dòng)作
我們定義三種鄰域動(dòng)作:
Exchange:從被選擇的元素的集合中隨機(jī)選擇元素i,從不被選擇的元素的集合中隨機(jī)選擇元素j,交換i,j。
Insert:從不被選擇的元素中隨機(jī)選擇元素i,將其從不被選擇的元素的集合中移除,并加入到被選擇的元素的集合中。
Remove:?從被選擇的元素的集合中隨機(jī)選擇元素i,將其從被選擇的元素的集合中移除,并加入到不被選擇的元素的集合中。
3.3
具體流程
shake函數(shù):我們定義shake函數(shù)接受參數(shù)k,隨機(jī)從選擇的元素的集合和不被選擇的元素的集合中選擇k個(gè)元素,并交換他們。
通過(guò)我們?cè)?strong>3.2中定義的鄰域動(dòng)作進(jìn)行進(jìn)行搜索,具體流程如下圖:

Part
4
代碼分享
這里我們分享兩份代碼,第一份是某位西班牙大佬分享的代碼,另一種是小編在他的基礎(chǔ)上改編而來(lái)的代碼,這里展示的是小編實(shí)現(xiàn)的版本。在https://github.com/alexfp95/Max-Mean-Dispersion-Problem/tree/master/src中,可以獲得西班牙大佬寫(xiě)的版本。
具體實(shí)現(xiàn)如下:
1import?java.io.*;
2import?java.util.ArrayList;
3import?java.util.LinkedList;
4import?java.util.Queue;
5import?java.util.Random;
6
7class?Solution //解的類
8{
9????ArrayList?select_set?=?new?ArrayList<>();//存放點(diǎn)的集合
10????ArrayList?unselect_set?=?new?ArrayList<>();//沒(méi)選擇的點(diǎn)
11????double?value;
12????double?getValue()
13????{
14????????double?ans?=?0;
15????????ArrayList?new_set?=?new?ArrayList<>();
16????????new_set.addAll(this.select_set);
17????????while(new_set.size()!=0)
18????????{
19????????????int?i?=?new_set.get(0);
20????????????new_set.remove(0);
21????????????for(Integer?j:new_set)
22????????????{
23????????????????ans+=main.cost_mariax[i][j];
24????????????}
25????????}
26????????ans?=?ans?/?this.select_set.size();
27????????return?ans;?//?返回目標(biāo)函數(shù)值
28????}
29????double?improve_value(int?i)//計(jì)算返回將這個(gè)點(diǎn)轉(zhuǎn)到另一個(gè)集合后,value值的改變
30????{
31????????double?ans;
32????????double?last_ans?=?this.value;
33????????Integer?I?=?Integer.valueOf(i);
34????????Solution?new_solution?=?new?Solution();
35????????new_solution.select_set.addAll(this.select_set);
36????????if(this.select_set.contains(i))
37????????{
38
39????????????new_solution.select_set.remove(I);
40????????????new_solution.unselect_set.add(I);
41????????????ans?=?new_solution.getValue()?-?last_ans;
42????????}
43????????else
44????????{
45????????????new_solution.select_set.remove(I);
46????????????new_solution.unselect_set.add(I);
47????????????ans?=?new_solution.getValue()?-?last_ans;
48
49????????}
50????????return?ans;
51????}
52
53
54}
55abstract?class?Strategy//策略類,存放算法
56{
57
58????static?Solution?ini_solution()//初始化一個(gè)解,采用貪婪的思想,最開(kāi)始所有解都在select_set中,隨后逐漸減少,每次計(jì)算去除點(diǎn)的價(jià)值,由大到小,不再有改進(jìn)
59????{
60????????Solution?solution?=?new?Solution();
61????????for(int?i=1;i<=main.CODE_NUMBER;i++)
62????????????solution.select_set.add(i);//開(kāi)始時(shí)所有解都在select_set中
63????????solution.value?=?solution.getValue();//獲得當(dāng)前解
64????????double?best?=?0;
65????????int?id?=?0;
66????????while(true)?{
67????????????best?=?0;
68????????????for?(int?i?:?solution.select_set)?{
69????????????????//System.out.println(solution.improve_value(i));
70????????????????if?(best? 71????????????????????best?=?solution.improve_value(i);
72????????????????????id?=?i;
73????????????????}
74????????????????//System.out.println(solution.select_set.size());
75????????????}
76????????????if(best?==?0)
77????????????????break;
78????????????solution.select_set.remove(Integer.valueOf(id));//不斷改進(jìn)
79????????????solution.unselect_set.add(Integer.valueOf(id));
80????????????solution.value?=?solution.getValue();
81???????????//?System.out.println(solution.value);
82
83????????}
84????????solution.value?=?solution.getValue();
85????????return?solution;
86????}
87
88????static?Solution?exchange(Solution?solution)//第一種鄰域算子:交換i,j st i在solution中,j不在
89????{
90????????Random?r?=?new?Random();
91????????int?i?=?r.nextInt(solution.select_set.size()-1);
92????????int?j?=?r.nextInt(solution.unselect_set.size()-1);//在i,j中隨機(jī)找兩點(diǎn);
93????????Integer?mid_one?=?solution.select_set.get(i);
94????????Integer?mid_two?=?solution.unselect_set.get(j);
95????????solution.select_set.remove(i);
96????????solution.unselect_set.remove(j);
97????????solution.unselect_set.add(Integer.valueOf(mid_one));
98????????solution.select_set.add(Integer.valueOf(mid_two));
99????????solution.value?=?solution.getValue();
100????????return?solution;
101????}
102????static?Solution?insert(Solution?solution)//第二種鄰域算子:將j從沒(méi)選擇的集合中加入到solution中
103????{
104????????Random?r?=?new?Random();
105????????int?j?=??r.nextInt(solution.unselect_set.size()-1);
106????????int?mid?=?solution.unselect_set.get(j);
107????????solution.unselect_set.remove(j);
108????????solution.select_set.add(Integer.valueOf(mid));
109????????solution.value??=?solution.getValue();
110????????return?solution;
111????}
112????static?Solution?remove(Solution?solution)//第三種鄰域算子:將j從選擇的集合中刪除
113????{
114????????Random?r?=?new?Random();
115????????int?j?=?r.nextInt(solution.select_set.size()-1);
116????????int?mid?=?solution.select_set.get(j);
117????????solution.unselect_set.add(Integer.valueOf(mid));
118????????solution.value?=?solution.getValue();
119????????return?solution;
120????}
121????public??static?Solution?shake(Solution?solution,int?k)//shake動(dòng)作,跳出局部最優(yōu)
122????{
123????????for(int?i=1;i<=k;i++)
124????????{
125????????????solution?=?exchange(solution);
126????????}
127????????return??solution;
128????}
129????public?static?Solution?Local_Search(Solution?solution)//鄰域搜索,獲得局部最優(yōu)
130????{
131????????for(int?i=1;i<=100;i++)
132????????{
133????????????Solution?new_solution?=?new?Solution();
134????????????new_solution.select_set.addAll(solution.select_set);
135????????????new_solution.unselect_set.addAll(solution.unselect_set);
136????????????new_solution.value?=?solution.value;
137????????????if(solution.unselect_set.size()==0)
138????????????{
139????????????????new_solution?=?Strategy.remove(solution);
140????????????}
141????????????else?if(solution.select_set.size()==0)
142????????????{
143????????????????new_solution?=?Strategy.remove(solution);
144????????????}
145????????????else?{
146????????????????Random?r?=??new?Random();
147????????????????double?t?=?r.nextDouble();
148????????????????if(t>0.6)?{
149????????????????????new_solution?=?Strategy.exchange(new_solution);
150????????????????}
151????????????????else?if(t>0.3)
152????????????????{
153????????????????????new_solution?=?Strategy.remove(new_solution);
154
155????????????????}
156????????????????else
157????????????????{
158????????????????????new_solution?=?Strategy.insert(new_solution);
159????????????????}
160
161????????????}
162????????????if(solution.valuevalue)?{
163????????????????solution?=?new_solution;
164????????????????System.out.println(new_solution.value);
165????????????}
166????????}
167????????return?solution;
168????}
169????public?static?Solution?V_N_Search(Solution?solution)//變鄰域搜索
170????{
171????????int?k?=?1;
172????????{
173????????????while(k<=solution.select_set.size())//按照shaking的定義進(jìn)行shake,不斷搜索直到k==被選擇的集合的元素個(gè)數(shù)
174????????????{
175????????????????System.out.println(k);
176????????????????Solution?new_solution?=?new?Solution();
177????????????????new_solution.select_set.addAll(solution.select_set);
178????????????????new_solution.unselect_set.addAll(solution.unselect_set);
179????????????????new_solution.value?=?solution.value;
180????????????????new_solution?=?shake(new_solution,k);
181????????????????new_solution?=?Local_Search(new_solution);
182????????????????if(solution.valuevalue)
183????????????????{
184????????????????????solution?=?new_solution;
185????????????????????k=1;
186????????????????}
187????????????????else{
188????????????????????k++;
189????????????????}
190????????????????System.out.println(solution.value);
191
192????????????}
193????????}
194????????return?solution;
195????}
196}
197public?class?main?{
198????static?double[][]?cost_mariax;//距離矩陣
199????static?int?CODE_NUMBER;
200????public?static?void?main(String[]?args)
201????{
202????????CODE_NUMBER?=?150;
203????????cost_mariax?=?new?double[CODE_NUMBER+1][CODE_NUMBER+1];//初始化
204????????for(int?i=1;i<=CODE_NUMBER;i++)
205????????try?{
206????????????FileReader?fr?=?new?FileReader("MDPI1_150.txt");//讀入數(shù)據(jù)
207????????????BufferedReader?br?=?new?BufferedReader(fr);
208????????????String?line?=?"?";
209????????????while(true)
210????????????{
211????????????????line?=?br.readLine();
212????
213????????????????if(line.equals("end"))break;
214????????????????String?data[]?=?line.split("\t");
215????????????????cost_mariax[Integer.valueOf(data[0])][Integer.valueOf(data[1])]?=?Double.valueOf(data[2]);
216????????????????cost_mariax[Integer.valueOf(data[1])][Integer.valueOf(data[0])]?=?Double.valueOf(data[2]);
217
218????????????}
219????????}
220????????catch(IOException?e)
221????????{
222????????????e.printStackTrace();
223????????}
224
225??????
226????????for(int?i=1;i<=CODE_NUMBER;i++) //初始化
227????????????for(int?j=1;j<=CODE_NUMBER;j++)
228????????????{
229????????????????if(i?==?j)
230????????????????{
231????????????????????cost_mariax[i][j]?=?0;
232????????????????????continue;
233????????????????}
234
235
236????????????}
237????????????Solution?solution?=?Strategy.ini_solution(); //?初始化解;
239????????????solution?=?Strategy.V_N_Search(solution);//VNS搜索
240????????????System.out.println(solution.value);
241????????????System.out.println("當(dāng)前解為"+solution.value);
242????????????System.out.println("被選擇的點(diǎn)集的大小為"?+?solution.select_set.size());
243
244
245????}
246}
結(jié)果如圖:

欲下載本文相關(guān)代碼,測(cè)試樣例,相關(guān)論文,請(qǐng)移步留言區(qū)
參考文獻(xiàn):
[1]Martí, Rafael, and Fernando Sandoya. “GRASP and Path Relinking for the Equitable Dispersion Problem.” Computers & Operations Research 40.12 (2013): 3091–3099. Crossref. Web.
[2] Hansen, Pierre , and N. Mladenovi?. "Variable neighborhood search: Principles and applications."?European Journal of Operational Research?130.3(2001):449-467.
[3]Hansen, Pierre, N. Mladenovi?, and D. Perez-Britos. "Variable Neighborhood Decomposition Search."?Journal of Heuristics?7.4(2001):335-350.


-The End-
文案/代碼/排版?:李博驍
指導(dǎo)老師 / 秦虎 華中科技大學(xué)管理學(xué)院?
如對(duì)代碼有疑問(wèn),可聯(lián)系小編,無(wú)償提供服務(wù)。
李博驍(華中科技大學(xué)管理學(xué)院本科二年級(jí)、[email protected])
