模擬退火(SA)算法求解Max-Minsum Dispersion Problem(附代碼及詳細(xì)注釋?zhuān)?/h1>
Part 1 Max-Minsum Dispersion Problem
先來(lái)看一個(gè)小故事,轉(zhuǎn)自(鏈接:http://blog.csdn.net/fudan_abc/article/details/2052642),假如老板要你解決一個(gè)問(wèn)題,你絞盡腦汁還是想不出來(lái),叫天天不應(yīng),叫地地不靈,這時(shí)你走進(jìn)老板辦公室,可以采取3種策略:

(1)一副倒霉像,神情ws,可憐巴巴的說(shuō):老板,我沒(méi)做出來(lái),我想我是太蠢了。。。
boss:蠢材!滾!
(失敗。。。)

(2)雄赳赳氣昂昂跨進(jìn)老板辦公室,大吼一聲:小樣,你丫給我問(wèn)題根本就無(wú)解,害我白想這么些天,我靠!
boss:我才靠,自己做不出來(lái)就說(shuō)這個(gè)問(wèn)題無(wú)解,要是人人都這樣混,我這老板還當(dāng)個(gè)屁啊,滾!
(做不出來(lái)還如此氣憤,不僅失敗,而且欠扁。。。)

(3)從容不迫的說(shuō):老板,我做不出來(lái),但是,我敢肯定,那些大牛們也照樣做不出來(lái)
boss:原來(lái)是這樣,那也難為你了。
把決策問(wèn)題可以按照難易程度分為幾類(lèi):
(1)P問(wèn)題:可以在多項(xiàng)式( polynomial )時(shí)間內(nèi)解決的問(wèn)題,稱(chēng)為P問(wèn)題。
(2)NP問(wèn)題:對(duì)于一類(lèi)問(wèn)題,我們可能沒(méi)有一個(gè)已知的快速的方法得到問(wèn)題的答案,但給定一個(gè)解,我們可以在P時(shí)間內(nèi)檢查他正確與否的決策問(wèn)題,成為NP( Non-deterministic polynomial)問(wèn)題。
(4)NP-hard問(wèn)題:用一句話概括他們的特征就是“at least as hard as the hardest problems in NP Problem”。
【多項(xiàng)式級(jí)時(shí)間復(fù)雜度:O(1),O(log(n)),O(n^a)等。因?yàn)橐?guī)模n出現(xiàn)在底數(shù)的位置。】
1.1 Max-Minsum Dispersion Problem
Max-Minsum DP就是一個(gè)典型的NP-Hard問(wèn)題,屬Equity-based dispersion problems,試圖從較大的集合中選擇一組元素時(shí)解決公平與效率的平衡,應(yīng)用廣泛然而計(jì)算難度較大。
簡(jiǎn)單來(lái)講,就是要從一個(gè)集合中選擇一個(gè)子集合,使得子集合中某個(gè)所選元素到其他所選元素之間距離的最小和最大化。
舉個(gè)例子,假如說(shuō)你一天要完成5個(gè)任務(wù),現(xiàn)在有10項(xiàng)任務(wù)供你選擇,煮飯30分鐘,做菜30分鐘,衣服機(jī)洗30分鐘,做作業(yè)20分鐘,燒開(kāi)水10分鐘,吃飯15分鐘等,你是個(gè)聰明的無(wú)聊人,知道有些活兒可以一起干以節(jié)省時(shí)間,又想讓這5項(xiàng)任務(wù)占用你更多的時(shí)間以打發(fā)無(wú)聊,這便是個(gè)簡(jiǎn)單的Max-Minsum DP。
再舉個(gè)更貼近實(shí)際的,對(duì)于網(wǎng)頁(yè)排名問(wèn)題,即是標(biāo)識(shí)網(wǎng)頁(yè)等級(jí)或重要性。最早的搜索引擎采用的是分類(lèi)目錄的方法,即通過(guò)人工對(duì)網(wǎng)頁(yè)進(jìn)行分類(lèi)并整理出高質(zhì)量網(wǎng)站。隨著網(wǎng)頁(yè)數(shù)目的急劇增大,這種方法顯然無(wú)法實(shí)現(xiàn),Larry Page和Sergey Brin受學(xué)術(shù)界對(duì)學(xué)術(shù)論文重要性的評(píng)估方法(論文引用次數(shù))的啟發(fā),提出了PageRank算法,如果一個(gè)網(wǎng)頁(yè)被很多其它網(wǎng)頁(yè)鏈接到,說(shuō)明這個(gè)網(wǎng)頁(yè)很重要,它的PageRank值也會(huì)相應(yīng)較高,如果一個(gè)PageRank值很高的網(wǎng)頁(yè)鏈接到另外某個(gè)網(wǎng)頁(yè),那么那個(gè)網(wǎng)頁(yè)的PageRank值也會(huì)相應(yīng)地提高。所以說(shuō)找重要論文、相關(guān)論文就不免涉及到Max-Minsum DP。
更多的應(yīng)用如下圖:
1.2 Max-Minsum DP的數(shù)學(xué)描述
考慮一個(gè)含有n個(gè)元素的集合N={1,2,...,n},每個(gè)元素包含著r個(gè)屬性,我們可以將一個(gè)元素用向量表示。問(wèn)題在于選擇N的一個(gè)子集M,|M|為固定正整數(shù)m(m這個(gè)距離有多種算法,如歐幾里得距離,曼哈頓距離等。在這里我們使用最為常用的歐幾里得距離
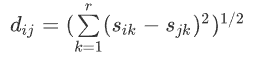
問(wèn)題可以表達(dá)為:
Part 2 模擬退火算法(SA)再回顧
在之前的推文【算法進(jìn)階】用模擬退火(SA, Simulated Annealing)算法解決旅行商問(wèn)題中,已經(jīng)對(duì)模擬退火算法有了詳細(xì)介紹并給出了偽代碼及實(shí)例。在這里,我們簡(jiǎn)要復(fù)習(xí),詳細(xì)參見(jiàn)以上推文。
2.1 SA算法介紹
模擬退火算法的基礎(chǔ)是metropolis算法。metropolis算法又稱(chēng)為metropolis抽樣,其核心思想是:當(dāng)能量增加的時(shí)候以一定概率接納,而非一味拒絕。
所以,當(dāng)Y(i+1)>Y(i),則無(wú)條件接受;
???當(dāng)Y(i+1)??以一定概率接受一個(gè)比當(dāng)前解較差的解,從而在一定程度上避免陷入局部最優(yōu)。
??然而應(yīng)當(dāng)如何計(jì)算這個(gè)概率呢?根據(jù)熱力學(xué)的原理,在溫度為T(mén)時(shí),出現(xiàn)能量差為dE的降溫的概率為P(dE),
表示為:
其中k是一個(gè)常數(shù),且dE<0(溫度總是降低的)。
1)溫度越高,出現(xiàn)一次能量差為dE的降溫的概率就越大。
2)溫度越低,則出現(xiàn)降溫的概率就越小。
3)本問(wèn)題將內(nèi)能E模擬為目標(biāo)函數(shù)值 f。
Part 3 具體算法介紹
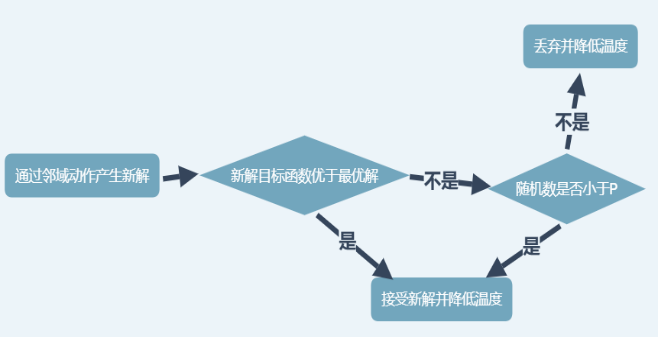
通過(guò)鄰域動(dòng)作產(chǎn)生新的集合M,產(chǎn)生新解及當(dāng)前解,計(jì)算即smallestDelta。 若當(dāng)前解的smallestDelta小于最優(yōu)解的smallestDelta,則更新最優(yōu)解為當(dāng)前解,否則以模擬退火的那個(gè)概率接受當(dāng)前解,然后降溫。 重復(fù)之前步驟,直到滿(mǎn)足退出條件。
現(xiàn)在拿一個(gè)小算例來(lái)操作一下:
現(xiàn)有一點(diǎn)集N={(0,1),(1,2),(3,4),(4,5),(6,6),(8,7)},我們要從中選出m個(gè)點(diǎn)構(gòu)成點(diǎn)集M,就取m=3吧,目標(biāo)函數(shù)是我們挑選的這3個(gè)點(diǎn)中的某一點(diǎn)到其余2個(gè)點(diǎn)的距離之和的最小值,而問(wèn)題在于找到使目標(biāo)函數(shù)值最大的那3個(gè)點(diǎn)。
3.1 初始解生成
就小算例而言,我們就隨機(jī)選3個(gè)點(diǎn),你不妨可以擲骰子,我擲的是5,2,1,那我們就取(6,6), (1,2), (0,1)這三個(gè)點(diǎn),不妨將這三個(gè)點(diǎn)重新標(biāo)記為,
以為中心點(diǎn),則;
以為中心點(diǎn),則;
以為中心點(diǎn),則;
不難看出,smallestDelta為Δ2,故初始解也是當(dāng)前最優(yōu)解即為M={(6,6),(1,2),(0,1)},對(duì)應(yīng)為。
??而就本問(wèn)題而言,對(duì)于初始解,我們亦是隨機(jī)產(chǎn)生,距離矩陣?yán)孟磁扑惴?strong>隨機(jī)生成1-100的距離,隨機(jī)選擇m個(gè)元素構(gòu)成s1,未被選中的即為s0,為了識(shí)別M和N\M,我們利用n維向量?= (?1 , ?2 , . . . , ?n ),其中,則,對(duì)應(yīng)的集合M即為初始解,也作為最優(yōu)解。
3.2 鄰域動(dòng)作
采用exchange算子:從被選擇的元素的集合中隨機(jī)選擇元素u,即u∈M,從不被選擇的元素的集合中隨機(jī)選擇元素v,即v∈N\M,交換u, v。拿上文小算例N={(0,1),(1,2),(3,4),(4,5),(6,6),(8,7)}舉個(gè)例子,從中隨機(jī)選擇,即∈M,從中隨機(jī)選擇,即∈N\M,交換,此時(shí)得到新解,以三點(diǎn)分別為中心點(diǎn),故不變得到
以為中心點(diǎn),則;
以為中心點(diǎn),則;
以為中心點(diǎn),則;
不難看出,smallestDelta為Δ2,故最優(yōu)解更新,變?yōu)镸={(4,5),(1,2),(0,1)},對(duì)應(yīng)為。
3.3 去重優(yōu)化
對(duì)于本問(wèn)題,給定鄰域解和對(duì)應(yīng)向量(?1 , ?2 , . . . , ?n ),目標(biāo)值可以在O(M)時(shí)間內(nèi)計(jì)算,此外,若是兩個(gè)元素u∈M,v∈N\M交換,則向量?= (?1 , ?2 , . . . , ?n )可以在O(N)時(shí)間內(nèi)快速更新,具體可表示為下圖:
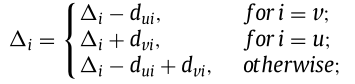
為了通俗易懂,接著拿上文小算例N={(0,1),(1,2),(3,4),(4,5),(6,6),(8,7)}舉例,比較3.1及3.2計(jì)算Δ過(guò)程不難看出,對(duì)于未改變的點(diǎn),即以為中心點(diǎn)、以為中心點(diǎn)時(shí),對(duì)應(yīng)的Δ計(jì)算過(guò)程只改變了一半,這部分就是我們可以?xún)?yōu)化的部分,因?yàn)榱硗庖话胛覀兙筒挥迷僦貜?fù)計(jì)算了,
;
;
當(dāng)數(shù)據(jù)越來(lái)越龐大之后,這部分優(yōu)化帶來(lái)的效益就會(huì)體現(xiàn)得更加明顯,時(shí)間復(fù)雜度大幅減少。
而對(duì)于改變的點(diǎn),
,
基本上就是重算。
Part 4 代碼分享
算例為隨機(jī)生成,具體實(shí)現(xiàn)如下:
#include
#include
#include
#include
#include
const?int?MAX?=?0x7fffffff;
const?int?N?=?1000;??//最大的范圍
const?int?M?=?500;??//要選擇的集合大小
const?int?K?=?100;??//兩點(diǎn)間距離的最大值為K(距離默認(rèn)為1-K)
const?int?max_count?=?10;?//當(dāng)前溫度的最大迭代次數(shù)
const?double?T0?=?50000.0;?//初始溫度
const?double?T_end?=?1e-8;?//退火結(jié)束溫度
const?double?q?=?0.98;?//退火系數(shù)
int*?elements;?//共計(jì)N個(gè)點(diǎn)
int**?distance;??//距離矩陣
clock_t?start_total,?end_total;??//計(jì)時(shí)器,整個(gè)程序
clock_t?start_delta,?end_delta;??//計(jì)時(shí)器,直接計(jì)算delta的步驟
struct?Solution?//解
{
?int*?s0;?//未被選中的數(shù)
?int*?s1;?//被選中的數(shù)
?int*?delta;?//到其他s1中的數(shù)的距離和
?int?smallestDelta;?//最大的delta,及目標(biāo)函數(shù)值
?int?center;?//核心數(shù)
}iniSolution,?bestSolution,solution1;
//分配存儲(chǔ)空間
void?init_solution(Solution*?s)
{
?s->s0?=?new?int[M];
?s->s1?=?new?int[N?-?M];
?s->delta?=?new?int[M];
?s->smallestDelta?=?0;
}
//撤銷(xiāo)iniSolution,?bestSolution,solution1所占存儲(chǔ)空間
void?dispose(Solution*?s)
{
?delete[](s->s0);s->s0?=?NULL;
?delete[](s->s1);s->s1?=?NULL;
?delete[](s->delta);s->delta?=?NULL;
}
//深拷貝solution類(lèi)型
void?copy_solution(Solution*?ini,?Solution*?obj)
{
?for?(int?i?=?0;?i???obj->s1[i]?=?ini->s1[i];
?for?(int?i?=?0;?i???obj->s0[i]?=?ini->s0[i];
?for?(int?i?=?0;?i???obj->delta[i]?=?ini->delta[i];
?obj->smallestDelta?=?ini->smallestDelta;
?obj->center?=?ini->center;
}
//計(jì)算所有delta的值
void?calculate_delta(Solution*?s)
{
?for?(int?i?=?0;?i??{
??s->delta[i]?=?0;
??for?(int?j?=?0;?j????s->delta[i]?+=?distance[s->s1[i]][s->s1[j]];
?}
}
//?在所有delta中找出smallest?delta以及對(duì)應(yīng)的中心數(shù)
void?calculate_sum(Solution*?s)
{
?s->smallestDelta?=?s->delta[0];
?s->center?=?s->s1[0];
?for?(int?i?=?0;?i??{
??if?(s->delta[i]?smallestDelta)
??{
???s->smallestDelta?=?s->delta[i];
???s->center?=?s->s1[i];
??}
?}
}
//更新的方法算出delta的值(將s0[v]與s1[u]交換)
void?update_delta(Solution*?s,?int?u,?int?v,?int?deltav)
{
?for?(int?i?=?0;?i??{
??if?(i?==?u)??//其自身delta的改變
???s->delta[u]?=?deltav?-?distance[s->s0[v]][s->s1[u]];
??else???//其他delta需將與s1[u]的距離轉(zhuǎn)換為與s0[v]的距離
???s->delta[i]?=?s->delta[i]?-?distance[s->s1[u]][s->s1[i]]?+?distance[s->s0[v]][s->s1[i]];
?}
}
void?init()
{
?//為距離矩陣隨機(jī)生成1-100的距離
?for?(int?i?=?0;i???for?(int?j?=?0;j?//因?yàn)榫嚯x矩陣是對(duì)稱(chēng)的
???distance[i][j]?=?distance[j][i]?=?rand()?%?K?+?1;?//距離為1-K
?for?(int?i?=?0;i???distance[i][i]?=?0;
?//隨機(jī)生成初始解
?for?(int?i?=?0;?i???elements[i]?=?i;
?//洗牌算法打亂
?for?(int?i?=?0;?i??{
??int?index?=?rand()?%?(N?-?i)?+?i;
??if?(index?!=?i)
??{
???int?temp?=?elements[i];
???elements[i]?=?elements[index];
???elements[index]?=?temp;
??}
?}
?//初始化,分配數(shù)組空間
?init_solution(&iniSolution);
?//前M個(gè)為s1,后面為s0
?for?(int?i?=?0;i???iniSolution.s1[i]?=?elements[i];
?for?(int?i?=?M,?j?=?0;i???iniSolution.s0[j]?=?elements[i];
?//計(jì)算delta
?start_delta?=?clock();
?calculate_delta(&iniSolution);
?end_delta?=?clock();
?//計(jì)算smallest_delta
?calculate_sum(&iniSolution);
?//bestSolution拷貝iniSolution
?init_solution(&bestSolution);
?copy_solution(&iniSolution,?&bestSolution);
?dispose(&iniSolution);
?//for?(int?i?=?0;i?
}
void?SA_search()?//模擬退火算法Simulated?Annealing
{
?srand((unsigned)time(NULL));?//初始化隨機(jī)數(shù)種子
?double?T?=?T0;?//初始溫度
?int?count_total?=?0;?//記錄降溫次數(shù)
?while?(T?>?T_end)?//?當(dāng)溫度低于結(jié)束溫度時(shí),退火結(jié)束
?{
??for?(int?count?=?0;count?<=?max_count;count++)?//count記錄當(dāng)前溫度迭代次數(shù)
??{
???int?deltav?=?0;?//計(jì)算deltav
???//產(chǎn)生新解solution1
???init_solution(&solution1);
???copy_solution(&bestSolution,?&solution1);
???double?r1?=?((double)rand())?/?(RAND_MAX?+?1.0);
???double?r2?=?((double)rand())?/?(RAND_MAX?+?1.0);
???int?v?=?(int)((N?-?M)?*?r1);?//s0中交換點(diǎn)的位置
???int?u?=?(int)(M?*?r2);?//s1中交換點(diǎn)的位置
???for?(int?u?=?0;u?//對(duì)選中的數(shù)(s1)進(jìn)行循環(huán)
????deltav?+=?distance[bestSolution.s0[v]][bestSolution.s1[u]];
???update_delta(&solution1,?u,?v,?deltav);
???int?temp?=?solution1.s0[v];
???solution1.s0[v]?=?solution1.s1[u];
???solution1.s1[u]?=?temp;
???calculate_sum(&solution1);?//計(jì)算smallest_delta
???double?f1,?f2,?df;
???f1?=?bestSolution.smallestDelta;
???f2?=?solution1.smallestDelta;
???df?=?f2?-?f1;
???double?r?=?((double)rand())?/?(RAND_MAX);?//0-1之間的隨機(jī)數(shù),用來(lái)決定是否接受新解
???if?(df?>=?0)
????copy_solution(&solution1,?&bestSolution);
???else?if?(r?exp(df?/?T))?//若隨機(jī)數(shù)小于p,接受新解
????copy_solution(&solution1,?&bestSolution);
???dispose(&solution1);
???count++;
??}
??T?*=?q;?//降溫
??count_total++;
??std::cout?<"第"?<"次降溫,?當(dāng)前溫度:"?<",當(dāng)前最優(yōu)解:"?<std::endl;
?}
}
void?print_info()
{
?std::cout?<"max-min?sum?answer:"?<std::endl;
?std::cout?<"one?delta?run?time:"?<double)(end_delta?-?start_delta)?/?CLOCKS_PER_SEC?<std::endl;
?std::cout?<"total?run?time:"?<double)(end_total?-?start_total)?/?CLOCKS_PER_SEC?<std::endl;
?std::cout?<"模擬退火算法,初始溫度T0="?<",降溫系數(shù)q="?<",每個(gè)溫度迭代"?<"次"?<std::endl;
}
int?main()
{
?//初始化數(shù)組,分配空間
?elements?=?new?int[N];
?distance?=?new?int*?[N];
?for?(int?i?=?0;i???distance[i]?=?new?int[N];
?init();
?start_total?=?clock();
?SA_search();?//模擬退火算法進(jìn)行搜索
?end_total?=?clock();
?//打印結(jié)果
?print_info();
?dispose(&bestSolution);
?delete[]elements;
?for?(int?i?=?0;i???delete[]distance[i];
?delete[]distance;
?system("pause");
?return?0;
}
結(jié)果如圖: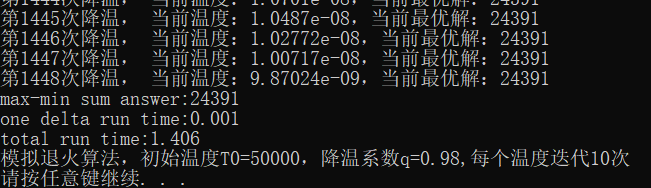
欲下載本文相關(guān)代碼,請(qǐng)移步留言區(qū)
參考文獻(xiàn):
xiangjing Lai,Dong Yue,Jin-Kao Hao,Fred Glover "Solution-based tabu search for the maximum min-sum dispersion problem." Information Sciences 441 (2018) 79-94.
-The End-
文案/代碼/排版:朱正雄
指導(dǎo)學(xué)長(zhǎng):周航
指導(dǎo)老師:秦虎? 華中科技大學(xué)管理學(xué)院
如對(duì)代碼有疑問(wèn),可聯(lián)系這個(gè)初出茅廬的小編。
朱正雄(華中科技大學(xué)管理學(xué)院本科一年級(jí)、[email protected])
瀏覽
56
Part 1 Max-Minsum Dispersion Problem
先來(lái)看一個(gè)小故事,轉(zhuǎn)自(鏈接:http://blog.csdn.net/fudan_abc/article/details/2052642),假如老板要你解決一個(gè)問(wèn)題,你絞盡腦汁還是想不出來(lái),叫天天不應(yīng),叫地地不靈,這時(shí)你走進(jìn)老板辦公室,可以采取3種策略:

(1)一副倒霉像,神情ws,可憐巴巴的說(shuō):老板,我沒(méi)做出來(lái),我想我是太蠢了。。。
boss:蠢材!滾!
(失敗。。。)

(2)雄赳赳氣昂昂跨進(jìn)老板辦公室,大吼一聲:小樣,你丫給我問(wèn)題根本就無(wú)解,害我白想這么些天,我靠!
boss:我才靠,自己做不出來(lái)就說(shuō)這個(gè)問(wèn)題無(wú)解,要是人人都這樣混,我這老板還當(dāng)個(gè)屁啊,滾!
(做不出來(lái)還如此氣憤,不僅失敗,而且欠扁。。。)

(3)從容不迫的說(shuō):老板,我做不出來(lái),但是,我敢肯定,那些大牛們也照樣做不出來(lái)
boss:原來(lái)是這樣,那也難為你了。
把決策問(wèn)題可以按照難易程度分為幾類(lèi):
(1)P問(wèn)題:可以在多項(xiàng)式( polynomial )時(shí)間內(nèi)解決的問(wèn)題,稱(chēng)為P問(wèn)題。
(2)NP問(wèn)題:對(duì)于一類(lèi)問(wèn)題,我們可能沒(méi)有一個(gè)已知的快速的方法得到問(wèn)題的答案,但給定一個(gè)解,我們可以在P時(shí)間內(nèi)檢查他正確與否的決策問(wèn)題,成為NP( Non-deterministic polynomial)問(wèn)題。
(4)NP-hard問(wèn)題:用一句話概括他們的特征就是“at least as hard as the hardest problems in NP Problem”。
【多項(xiàng)式級(jí)時(shí)間復(fù)雜度:O(1),O(log(n)),O(n^a)等。因?yàn)橐?guī)模n出現(xiàn)在底數(shù)的位置。】
1.1 Max-Minsum Dispersion Problem
Max-Minsum DP就是一個(gè)典型的NP-Hard問(wèn)題,屬Equity-based dispersion problems,試圖從較大的集合中選擇一組元素時(shí)解決公平與效率的平衡,應(yīng)用廣泛然而計(jì)算難度較大。
簡(jiǎn)單來(lái)講,就是要從一個(gè)集合中選擇一個(gè)子集合,使得子集合中某個(gè)所選元素到其他所選元素之間距離的最小和最大化。
舉個(gè)例子,假如說(shuō)你一天要完成5個(gè)任務(wù),現(xiàn)在有10項(xiàng)任務(wù)供你選擇,煮飯30分鐘,做菜30分鐘,衣服機(jī)洗30分鐘,做作業(yè)20分鐘,燒開(kāi)水10分鐘,吃飯15分鐘等,你是個(gè)聰明的無(wú)聊人,知道有些活兒可以一起干以節(jié)省時(shí)間,又想讓這5項(xiàng)任務(wù)占用你更多的時(shí)間以打發(fā)無(wú)聊,這便是個(gè)簡(jiǎn)單的Max-Minsum DP。
再舉個(gè)更貼近實(shí)際的,對(duì)于網(wǎng)頁(yè)排名問(wèn)題,即是標(biāo)識(shí)網(wǎng)頁(yè)等級(jí)或重要性。最早的搜索引擎采用的是分類(lèi)目錄的方法,即通過(guò)人工對(duì)網(wǎng)頁(yè)進(jìn)行分類(lèi)并整理出高質(zhì)量網(wǎng)站。隨著網(wǎng)頁(yè)數(shù)目的急劇增大,這種方法顯然無(wú)法實(shí)現(xiàn),Larry Page和Sergey Brin受學(xué)術(shù)界對(duì)學(xué)術(shù)論文重要性的評(píng)估方法(論文引用次數(shù))的啟發(fā),提出了PageRank算法,如果一個(gè)網(wǎng)頁(yè)被很多其它網(wǎng)頁(yè)鏈接到,說(shuō)明這個(gè)網(wǎng)頁(yè)很重要,它的PageRank值也會(huì)相應(yīng)較高,如果一個(gè)PageRank值很高的網(wǎng)頁(yè)鏈接到另外某個(gè)網(wǎng)頁(yè),那么那個(gè)網(wǎng)頁(yè)的PageRank值也會(huì)相應(yīng)地提高。所以說(shuō)找重要論文、相關(guān)論文就不免涉及到Max-Minsum DP。
更多的應(yīng)用如下圖:
1.2 Max-Minsum DP的數(shù)學(xué)描述
考慮一個(gè)含有n個(gè)元素的集合N={1,2,...,n},每個(gè)元素包含著r個(gè)屬性,我們可以將一個(gè)元素用向量表示。問(wèn)題在于選擇N的一個(gè)子集M,|M|為固定正整數(shù)m(m 這個(gè)距離有多種算法,如歐幾里得距離,曼哈頓距離等。在這里我們使用最為常用的歐幾里得距離 問(wèn)題可以表達(dá)為: 在之前的推文【算法進(jìn)階】用模擬退火(SA, Simulated Annealing)算法解決旅行商問(wèn)題中,已經(jīng)對(duì)模擬退火算法有了詳細(xì)介紹并給出了偽代碼及實(shí)例。在這里,我們簡(jiǎn)要復(fù)習(xí),詳細(xì)參見(jiàn)以上推文。 模擬退火算法的基礎(chǔ)是metropolis算法。metropolis算法又稱(chēng)為metropolis抽樣,其核心思想是:當(dāng)能量增加的時(shí)候以一定概率接納,而非一味拒絕。 現(xiàn)在拿一個(gè)小算例來(lái)操作一下: 就小算例而言,我們就隨機(jī)選3個(gè)點(diǎn),你不妨可以擲骰子,我擲的是5,2,1,那我們就取(6,6), (1,2), (0,1)這三個(gè)點(diǎn),不妨將這三個(gè)點(diǎn)重新標(biāo)記為, 采用exchange算子:從被選擇的元素的集合中隨機(jī)選擇元素u,即u∈M,從不被選擇的元素的集合中隨機(jī)選擇元素v,即v∈N\M,交換u, v。拿上文小算例N={(0,1),(1,2),(3,4),(4,5),(6,6),(8,7)}舉個(gè)例子,從中隨機(jī)選擇,即∈M,從中隨機(jī)選擇,即∈N\M,交換,此時(shí)得到新解,以三點(diǎn)分別為中心點(diǎn),故不變得到 對(duì)于本問(wèn)題,給定鄰域解和對(duì)應(yīng)向量(?1 , ?2 , . . . , ?n ),目標(biāo)值可以在O(M)時(shí)間內(nèi)計(jì)算,此外,若是兩個(gè)元素u∈M,v∈N\M交換,則向量?= (?1 , ?2 , . . . , ?n )可以在O(N)時(shí)間內(nèi)快速更新,具體可表示為下圖: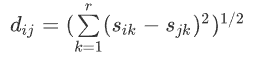

Part 2 模擬退火算法(SA)再回顧
2.1 SA算法介紹
所以,當(dāng)Y(i+1)>Y(i),則無(wú)條件接受;
???當(dāng)Y(i+1)
??然而應(yīng)當(dāng)如何計(jì)算這個(gè)概率呢?根據(jù)熱力學(xué)的原理,在溫度為T(mén)時(shí),出現(xiàn)能量差為dE的降溫的概率為P(dE),
表示為:
1)溫度越高,出現(xiàn)一次能量差為dE的降溫的概率就越大。
2)溫度越低,則出現(xiàn)降溫的概率就越小。
3)本問(wèn)題將內(nèi)能E模擬為目標(biāo)函數(shù)值 f。Part 3 具體算法介紹

現(xiàn)有一點(diǎn)集N={(0,1),(1,2),(3,4),(4,5),(6,6),(8,7)},我們要從中選出m個(gè)點(diǎn)構(gòu)成點(diǎn)集M,就取m=3吧,目標(biāo)函數(shù)是我們挑選的這3個(gè)點(diǎn)中的某一點(diǎn)到其余2個(gè)點(diǎn)的距離之和的最小值,而問(wèn)題在于找到使目標(biāo)函數(shù)值最大的那3個(gè)點(diǎn)。3.1 初始解生成
以為中心點(diǎn),則;
以為中心點(diǎn),則;
以為中心點(diǎn),則;
不難看出,smallestDelta為Δ2,故初始解也是當(dāng)前最優(yōu)解即為M={(6,6),(1,2),(0,1)},對(duì)應(yīng)為。
??而就本問(wèn)題而言,對(duì)于初始解,我們亦是隨機(jī)產(chǎn)生,距離矩陣?yán)孟磁扑惴?strong>隨機(jī)生成1-100的距離,隨機(jī)選擇m個(gè)元素構(gòu)成s1,未被選中的即為s0,為了識(shí)別M和N\M,我們利用n維向量?= (?1 , ?2 , . . . , ?n ),其中,則,對(duì)應(yīng)的集合M即為初始解,也作為最優(yōu)解。3.2 鄰域動(dòng)作
以為中心點(diǎn),則;
以為中心點(diǎn),則;
以為中心點(diǎn),則;
不難看出,smallestDelta為Δ2,故最優(yōu)解更新,變?yōu)镸={(4,5),(1,2),(0,1)},對(duì)應(yīng)為。3.3 去重優(yōu)化
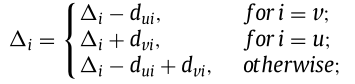
為了通俗易懂,接著拿上文小算例N={(0,1),(1,2),(3,4),(4,5),(6,6),(8,7)}舉例,比較3.1及3.2計(jì)算Δ過(guò)程不難看出,對(duì)于未改變的點(diǎn),即以為中心點(diǎn)、以為中心點(diǎn)時(shí),對(duì)應(yīng)的Δ計(jì)算過(guò)程只改變了一半,這部分就是我們可以?xún)?yōu)化的部分,因?yàn)榱硗庖话胛覀兙筒挥迷僦貜?fù)計(jì)算了,
;
;
當(dāng)數(shù)據(jù)越來(lái)越龐大之后,這部分優(yōu)化帶來(lái)的效益就會(huì)體現(xiàn)得更加明顯,時(shí)間復(fù)雜度大幅減少。
而對(duì)于改變的點(diǎn),
,
基本上就是重算。
Part 4 代碼分享
算例為隨機(jī)生成,具體實(shí)現(xiàn)如下:
#include
#include
#include
#include
#include
const?int?MAX?=?0x7fffffff;
const?int?N?=?1000;??//最大的范圍
const?int?M?=?500;??//要選擇的集合大小
const?int?K?=?100;??//兩點(diǎn)間距離的最大值為K(距離默認(rèn)為1-K)
const?int?max_count?=?10;?//當(dāng)前溫度的最大迭代次數(shù)
const?double?T0?=?50000.0;?//初始溫度
const?double?T_end?=?1e-8;?//退火結(jié)束溫度
const?double?q?=?0.98;?//退火系數(shù)
int*?elements;?//共計(jì)N個(gè)點(diǎn)
int**?distance;??//距離矩陣
clock_t?start_total,?end_total;??//計(jì)時(shí)器,整個(gè)程序
clock_t?start_delta,?end_delta;??//計(jì)時(shí)器,直接計(jì)算delta的步驟
struct?Solution?//解
{
?int*?s0;?//未被選中的數(shù)
?int*?s1;?//被選中的數(shù)
?int*?delta;?//到其他s1中的數(shù)的距離和
?int?smallestDelta;?//最大的delta,及目標(biāo)函數(shù)值
?int?center;?//核心數(shù)
}iniSolution,?bestSolution,solution1;
//分配存儲(chǔ)空間
void?init_solution(Solution*?s)
{
?s->s0?=?new?int[M];
?s->s1?=?new?int[N?-?M];
?s->delta?=?new?int[M];
?s->smallestDelta?=?0;
}
//撤銷(xiāo)iniSolution,?bestSolution,solution1所占存儲(chǔ)空間
void?dispose(Solution*?s)
{
?delete[](s->s0);s->s0?=?NULL;
?delete[](s->s1);s->s1?=?NULL;
?delete[](s->delta);s->delta?=?NULL;
}
//深拷貝solution類(lèi)型
void?copy_solution(Solution*?ini,?Solution*?obj)
{
?for?(int?i?=?0;?i???obj->s1[i]?=?ini->s1[i];
?for?(int?i?=?0;?i???obj->s0[i]?=?ini->s0[i];
?for?(int?i?=?0;?i???obj->delta[i]?=?ini->delta[i];
?obj->smallestDelta?=?ini->smallestDelta;
?obj->center?=?ini->center;
}
//計(jì)算所有delta的值
void?calculate_delta(Solution*?s)
{
?for?(int?i?=?0;?i??{
??s->delta[i]?=?0;
??for?(int?j?=?0;?j????s->delta[i]?+=?distance[s->s1[i]][s->s1[j]];
?}
}
//?在所有delta中找出smallest?delta以及對(duì)應(yīng)的中心數(shù)
void?calculate_sum(Solution*?s)
{
?s->smallestDelta?=?s->delta[0];
?s->center?=?s->s1[0];
?for?(int?i?=?0;?i??{
??if?(s->delta[i]?smallestDelta)
??{
???s->smallestDelta?=?s->delta[i];
???s->center?=?s->s1[i];
??}
?}
}
//更新的方法算出delta的值(將s0[v]與s1[u]交換)
void?update_delta(Solution*?s,?int?u,?int?v,?int?deltav)
{
?for?(int?i?=?0;?i??{
??if?(i?==?u)??//其自身delta的改變
???s->delta[u]?=?deltav?-?distance[s->s0[v]][s->s1[u]];
??else???//其他delta需將與s1[u]的距離轉(zhuǎn)換為與s0[v]的距離
???s->delta[i]?=?s->delta[i]?-?distance[s->s1[u]][s->s1[i]]?+?distance[s->s0[v]][s->s1[i]];
?}
}
void?init()
{
?//為距離矩陣隨機(jī)生成1-100的距離
?for?(int?i?=?0;i???for?(int?j?=?0;j?//因?yàn)榫嚯x矩陣是對(duì)稱(chēng)的
???distance[i][j]?=?distance[j][i]?=?rand()?%?K?+?1;?//距離為1-K
?for?(int?i?=?0;i???distance[i][i]?=?0;
?//隨機(jī)生成初始解
?for?(int?i?=?0;?i???elements[i]?=?i;
?//洗牌算法打亂
?for?(int?i?=?0;?i??{
??int?index?=?rand()?%?(N?-?i)?+?i;
??if?(index?!=?i)
??{
???int?temp?=?elements[i];
???elements[i]?=?elements[index];
???elements[index]?=?temp;
??}
?}
?//初始化,分配數(shù)組空間
?init_solution(&iniSolution);
?//前M個(gè)為s1,后面為s0
?for?(int?i?=?0;i???iniSolution.s1[i]?=?elements[i];
?for?(int?i?=?M,?j?=?0;i???iniSolution.s0[j]?=?elements[i];
?//計(jì)算delta
?start_delta?=?clock();
?calculate_delta(&iniSolution);
?end_delta?=?clock();
?//計(jì)算smallest_delta
?calculate_sum(&iniSolution);
?//bestSolution拷貝iniSolution
?init_solution(&bestSolution);
?copy_solution(&iniSolution,?&bestSolution);
?dispose(&iniSolution);
?//for?(int?i?=?0;i?
}
void?SA_search()?//模擬退火算法Simulated?Annealing
{
?srand((unsigned)time(NULL));?//初始化隨機(jī)數(shù)種子
?double?T?=?T0;?//初始溫度
?int?count_total?=?0;?//記錄降溫次數(shù)
?while?(T?>?T_end)?//?當(dāng)溫度低于結(jié)束溫度時(shí),退火結(jié)束
?{
??for?(int?count?=?0;count?<=?max_count;count++)?//count記錄當(dāng)前溫度迭代次數(shù)
??{
???int?deltav?=?0;?//計(jì)算deltav
???//產(chǎn)生新解solution1
???init_solution(&solution1);
???copy_solution(&bestSolution,?&solution1);
???double?r1?=?((double)rand())?/?(RAND_MAX?+?1.0);
???double?r2?=?((double)rand())?/?(RAND_MAX?+?1.0);
???int?v?=?(int)((N?-?M)?*?r1);?//s0中交換點(diǎn)的位置
???int?u?=?(int)(M?*?r2);?//s1中交換點(diǎn)的位置
???for?(int?u?=?0;u?//對(duì)選中的數(shù)(s1)進(jìn)行循環(huán)
????deltav?+=?distance[bestSolution.s0[v]][bestSolution.s1[u]];
???update_delta(&solution1,?u,?v,?deltav);
???int?temp?=?solution1.s0[v];
???solution1.s0[v]?=?solution1.s1[u];
???solution1.s1[u]?=?temp;
???calculate_sum(&solution1);?//計(jì)算smallest_delta
???double?f1,?f2,?df;
???f1?=?bestSolution.smallestDelta;
???f2?=?solution1.smallestDelta;
???df?=?f2?-?f1;
???double?r?=?((double)rand())?/?(RAND_MAX);?//0-1之間的隨機(jī)數(shù),用來(lái)決定是否接受新解
???if?(df?>=?0)
????copy_solution(&solution1,?&bestSolution);
???else?if?(r?exp(df?/?T))?//若隨機(jī)數(shù)小于p,接受新解
????copy_solution(&solution1,?&bestSolution);
???dispose(&solution1);
???count++;
??}
??T?*=?q;?//降溫
??count_total++;
??std::cout?<"第"?<"次降溫,?當(dāng)前溫度:"?<",當(dāng)前最優(yōu)解:"?<std::endl;
?}
}
void?print_info()
{
?std::cout?<"max-min?sum?answer:"?<std::endl;
?std::cout?<"one?delta?run?time:"?<double)(end_delta?-?start_delta)?/?CLOCKS_PER_SEC?<std::endl;
?std::cout?<"total?run?time:"?<double)(end_total?-?start_total)?/?CLOCKS_PER_SEC?<std::endl;
?std::cout?<"模擬退火算法,初始溫度T0="?<",降溫系數(shù)q="?<",每個(gè)溫度迭代"?<"次"?<std::endl;
}
int?main()
{
?//初始化數(shù)組,分配空間
?elements?=?new?int[N];
?distance?=?new?int*?[N];
?for?(int?i?=?0;i???distance[i]?=?new?int[N];
?init();
?start_total?=?clock();
?SA_search();?//模擬退火算法進(jìn)行搜索
?end_total?=?clock();
?//打印結(jié)果
?print_info();
?dispose(&bestSolution);
?delete[]elements;
?for?(int?i?=?0;i???delete[]distance[i];
?delete[]distance;
?system("pause");
?return?0;
}
結(jié)果如圖:
欲下載本文相關(guān)代碼,請(qǐng)移步留言區(qū)
參考文獻(xiàn):
xiangjing Lai,Dong Yue,Jin-Kao Hao,Fred Glover "Solution-based tabu search for the maximum min-sum dispersion problem." Information Sciences 441 (2018) 79-94.
-The End-
文案/代碼/排版:朱正雄
指導(dǎo)學(xué)長(zhǎng):周航
指導(dǎo)老師:秦虎? 華中科技大學(xué)管理學(xué)院
如對(duì)代碼有疑問(wèn),可聯(lián)系這個(gè)初出茅廬的小編。
朱正雄(華中科技大學(xué)管理學(xué)院本科一年級(jí)、[email protected])
