【機(jī)器學(xué)習(xí)】梯度下降的Python實(shí)現(xiàn)

作者 | Vagif Aliyev?

編譯 | VK?

來源 | Towards Data Science

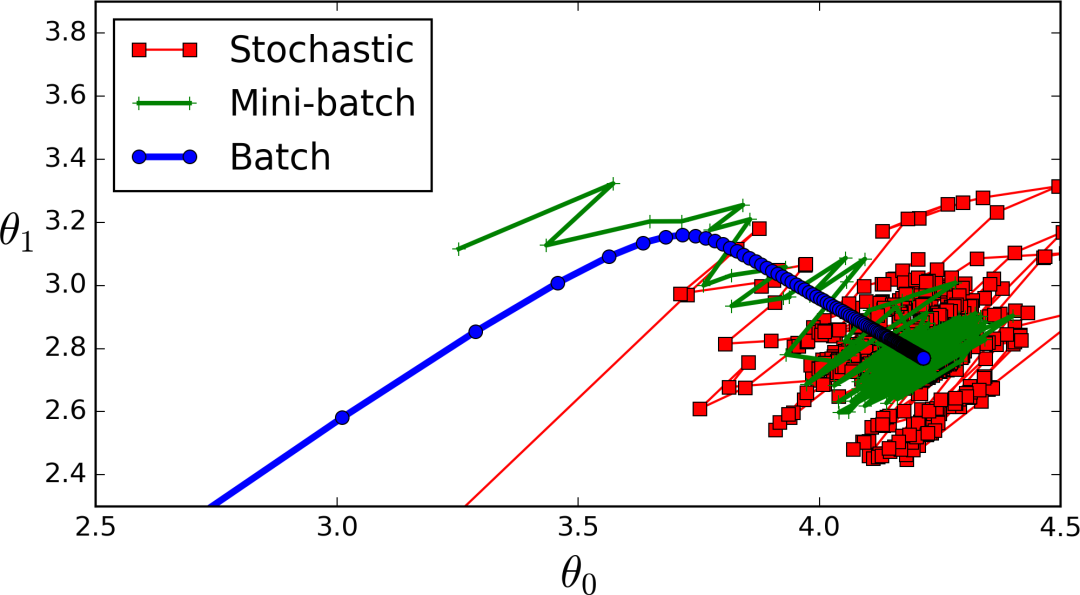
梯度下降是數(shù)據(jù)科學(xué)的基礎(chǔ)，無論是深度學(xué)習(xí)還是機(jī)器學(xué)習(xí)。對(duì)梯度下降原理的深入了解一定會(huì)對(duì)你今后的工作有所幫助。

你將真正了解這些超參數(shù)的作用、在背后發(fā)生的情況以及如何處理使用此算法可能遇到的問題，而不是玩弄超參數(shù)并希望獲得最佳結(jié)果。

然而，梯度下降并不局限于一種算法。另外兩種流行的梯度下降（隨機(jī)和小批量梯度下降）建立在主要算法的基礎(chǔ)上，你可能會(huì)看到比普通批量梯度下降更多的算法。因此，我們也必須對(duì)這些算法有一個(gè)堅(jiān)實(shí)的了解，因?yàn)樗鼈冇幸恍╊~外的超參數(shù)，當(dāng)我們的算法沒有達(dá)到我們期望的性能時(shí)，我們需要理解和分析這些超參數(shù)。

雖然理論對(duì)于深入理解手頭的算法至關(guān)重要，但梯度下降的實(shí)際編碼及其不同的“變體”可能是一項(xiàng)困難的任務(wù)。為了完成這項(xiàng)任務(wù)，本文的格式如下：

1. 簡(jiǎn)要概述每種算法的作用。

2. 算法的代碼

3. 對(duì)規(guī)范不明確部分的進(jìn)一步解釋

我們將使用著名的波士頓住房數(shù)據(jù)集，它是預(yù)先內(nèi)置在scikit learn中的。我們還將從頭開始構(gòu)建一個(gè)線性模型

好的，首先讓我們做一些基本的導(dǎo)入。我不打算在這里做EDA，因?yàn)檫@不是我們文章的真正目的。不過，我會(huì)把一些事情說明白。

import?numpy?as?np
import?pandas?as?pd?
import?plotly.express?as?px
from?sklearn.datasets?import?load_boston
from?sklearn.metrics?import?mean_squared_error

好的，為了讓我們看到數(shù)據(jù)是什么樣子，我將把數(shù)據(jù)轉(zhuǎn)換成一個(gè)數(shù)據(jù)幀并顯示輸出。

data?=?load_boston()

df?=?pd.DataFrame(data['data'],columns=data['feature_names'])
df.insert(13,'target',data['target'])
df.head(5)

好吧，這里沒什么特別的，我敢肯定你之前已經(jīng)類似實(shí)現(xiàn)過了。

現(xiàn)在，我們將定義我們的特征（X）和目標(biāo)（y）。我們還將定義我們的參數(shù)向量，將其命名為thetas，并將它們初始化為零。

X,y?=?df.drop('target',axis=1),df['target']

thetas?=?np.zeros(X.shape[1])

成本函數(shù)

回想一下，成本函數(shù)是衡量模型性能的東西，也是梯度下降的目標(biāo)。我們將使用的代價(jià)函數(shù)稱為均方誤差。公式如下：

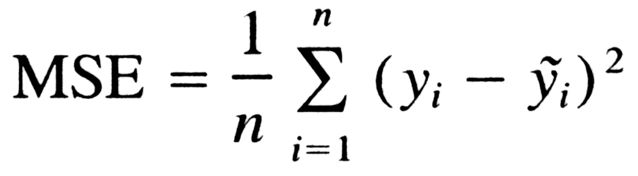
好吧，我們把它寫出來：

def?cost_function(X,Y,B):
????predictions?=?np.dot(X,B.T)
????
????cost?=?(1/len(Y))?*?np.sum((predictions?-?Y)?**?2)
????return?cost

在這里，我們將輸入、標(biāo)簽和參數(shù)作為輸入，并使用線性模型進(jìn)行預(yù)測(cè)，得到成本，然后返回。如果第二行讓你困惑，回想一下線性回歸公式：

所以，我們基本上是得到每個(gè)特征和它們相應(yīng)權(quán)重之間的點(diǎn)積。如果你還不確定我在說什么，看看這個(gè)視頻：https://www.youtube.com/watch?v=kHwlB_j7Hkc

很好，現(xiàn)在讓我們測(cè)試一下我們的成本函數(shù)，看看它是否真的有效。為了做到這一點(diǎn)，我們將使用scikit learn的均方誤差，得到結(jié)果，并將其與我們的算法進(jìn)行比較。

mean_squared_error(np.dot(X,thetas.T),y)

OUT:?592.14691169960474

cost_function(X,y,thetas)

OUT:?592.14691169960474

太棒了，我們的成本函數(shù)起作用了！

特征縮放

特征縮放是線性模型（線性回歸、KNN、SVM）的重要預(yù)處理技術(shù)。本質(zhì)上，特征被縮小到更小的范圍，并且特征也在一定的范圍內(nèi)。可以這樣考慮特征縮放：

1. 你有一座很大的建筑物

2. 你希望保持建筑的形狀，但希望將其調(diào)整為較小的比例

特征縮放通常用于以下場(chǎng)景：

1. 如果一個(gè)算法使用歐幾里德距離，那么由于歐幾里德距離對(duì)較大的量值敏感，因此需要對(duì)特征進(jìn)行縮放

2. 特征縮放還可以用于數(shù)據(jù)標(biāo)準(zhǔn)化

3. 特征縮放還可以提高算法的速度

雖然有許多不同的特征縮放方法，但我們將使用以下公式構(gòu)建MinMaxScaler的自定義實(shí)現(xiàn)：

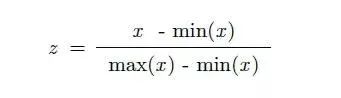
由于上述原因，我們將使用縮放。

現(xiàn)在，對(duì)于python實(shí)現(xiàn)：

X_norm?=?(X?-?X.min())?/?(X.max()?-?X.min())
X?=?X_norm

這里沒什么特別的，我們只是把公式翻譯成代碼。現(xiàn)在，節(jié)目真正開始了：梯度下降！

梯度下降

具體地說，梯度下降是一種優(yōu)化算法，它通過迭代遍歷數(shù)據(jù)并獲得偏導(dǎo)數(shù)來尋求函數(shù)的最小值（在我們的例子中是MSE）。

如果這有點(diǎn)復(fù)雜，試著把梯度下降想象成是一個(gè)人站在山頂上，他們?cè)囍宰羁斓乃俣葟纳缴吓老聛恚刂降呢?fù)方向不斷地“走”，直到到達(dá)底部。

現(xiàn)在，梯度下降有不同的版本，但是你會(huì)遇到最多的是：

1. 批量梯度下降

2. 隨機(jī)梯度下降法

3. 小批量梯度下降

現(xiàn)在我們將按順序討論、實(shí)現(xiàn)和分析每一項(xiàng)，所以讓我們開始吧！

批量梯度下降

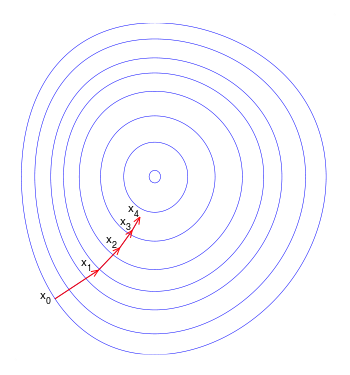
批量梯度下降可能是你遇到的第一種梯度下降類型。現(xiàn)在，我在這篇文章中并不是很理論化（你可以參考我以前的文章：https://medium.com/@vagifaliyev/gradient-descent-clearly-explained-in-python-part-1-the-troubling-theory-49a7fa2c4c06），但實(shí)際上它計(jì)算的是整個(gè)（批處理）數(shù)據(jù)集上系數(shù)的偏導(dǎo)數(shù)。你可能已經(jīng)猜到這樣做很慢了。

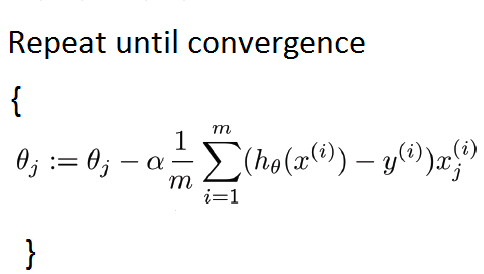
我們的數(shù)據(jù)集很小，所以我們可以像這樣實(shí)現(xiàn)批量梯度下降：

def?batch_gradient_descent(X,Y,theta,alpha,iters):
????cost_history?=?[0]?*?iters??#?初始化歷史損失列表
????for?i?in?range(iters):?????????
????????prediction?=?np.dot(X,theta.T)??????????????????
????????theta?=?theta?-?(alpha/len(Y))?*?np.dot(prediction?-?Y,X)???
????????cost_history[i]?=?cost_function(X,Y,theta)???????????????
????return?theta,cost_history

要澄清一些術(shù)語(yǔ)：

alpha：這是指學(xué)習(xí)率。

iters：迭代運(yùn)行的數(shù)量。

太好了，現(xiàn)在讓我們看看結(jié)果吧！

batch_theta,batch_history=batch_gradient_descent(X,y,theta,0.05,500)

好吧，不是很快，但也不是很慢。讓我們用我們新的和改進(jìn)的參數(shù)來可視化和成本：

cost_function(X,y,batch_theta)

OUT:?27.537447130784262

哇，從592到27！這只是一個(gè)梯度下降的力量的一瞥！讓我們對(duì)迭代次數(shù)的成本函數(shù)進(jìn)行可視化：

fig?=?px.line(batch_history,x=range(5000),y=batch_history,labels={'x':'no.?of?iterations','y':'cost?function'})
fig.show()

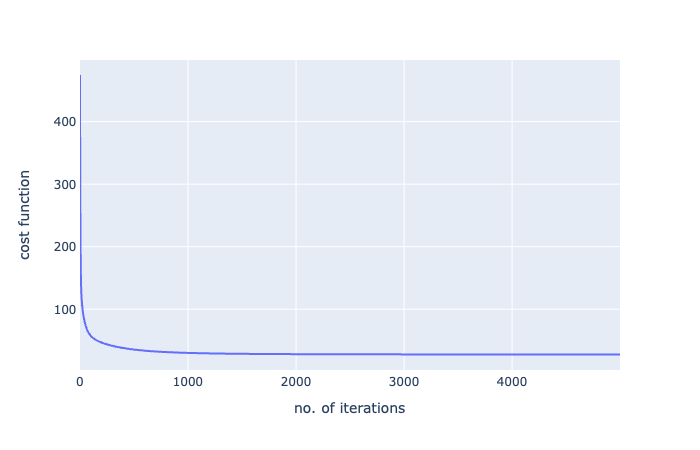
好的，看看這個(gè)圖表，我們?cè)诖蠹s100次迭代之后達(dá)到了一個(gè)大的下降，從那里開始，它一直在逐漸減少。

所以，批量梯度下降到此結(jié)束：

優(yōu)點(diǎn)

1. 有效且曲線平滑

2. 最準(zhǔn)確，最有可能達(dá)到全局最低值

缺點(diǎn)

1. 對(duì)于大型數(shù)據(jù)集可能會(huì)很慢

2. 計(jì)算成本高

隨機(jī)梯度下降法

這里，不是計(jì)算整個(gè)訓(xùn)練集的偏導(dǎo)數(shù)，而是只計(jì)算一個(gè)隨機(jī)樣本（隨機(jī)意義上的隨機(jī)）。

這是很好的，因?yàn)橛?jì)算只需要在一個(gè)訓(xùn)練示例上進(jìn)行，而不是在整個(gè)訓(xùn)練集上進(jìn)行，這使得計(jì)算速度更快，而且對(duì)于大型數(shù)據(jù)集來說非常理想。

然而，由于其隨機(jī)性，隨機(jī)梯度下降并不像批量梯度下降那樣具有平滑的曲線，雖然它可以返回良好的參數(shù)，但不能保證達(dá)到全局最小值。

學(xué)習(xí)率調(diào)整

解決隨機(jī)梯度下降問題的一種方法是學(xué)習(xí)率調(diào)整。

基本上，這會(huì)逐漸降低學(xué)習(xí)率。因此，學(xué)習(xí)率一開始很大（這有助于避免局部極小值），當(dāng)學(xué)習(xí)率接近全局最小值時(shí)，學(xué)習(xí)率逐漸降低。但是，你必須小心：

1. 如果學(xué)習(xí)速率降低得太快，那么算法可能會(huì)陷入局部極小，或者在達(dá)到最小值的一半時(shí)停滯不前。

2. 如果學(xué)習(xí)速率降低太慢，可能會(huì)在很長(zhǎng)一段時(shí)間內(nèi)跳轉(zhuǎn)到最小值附近，仍然無法得到最佳參數(shù)

現(xiàn)在，我們將使用簡(jiǎn)易的學(xué)習(xí)率調(diào)整策略實(shí)現(xiàn)隨機(jī)梯度下降：

t0,t1?=?5,50?#?學(xué)習(xí)率超參數(shù)

def?learning_schedule(t):
????return?t0/(t+t1)
????
def?stochastic_gradient_descent(X,y,thetas,n_epochs=30):
????c_hist?=?[0]?*?n_epochs?#?歷史成本
????for?epoch?in?range(n_epochs):
????????for?i?in?range(len(y)):
????????????random_index?=?np.random.randint(len(Y))
????????????xi?=?X[random_index:random_index+1]
????????????yi?=?y[random_index:random_index+1]
????????????
????????????prediction?=?xi.dot(thetas)
????????????
????????????gradient?=?2?*?xi.T.dot(prediction-yi)
????????????eta?=?learning_schedule(epoch?*?len(Y)?+?i)
????????????thetas?=?thetas?-?eta?*?gradient
????????????c_hist[epoch]?=?cost_function(xi,yi,thetas)
????return?thetas,c_hist

現(xiàn)在運(yùn)行函數(shù)：

sdg_thetas,sgd_cost_hist?=?stochastic_gradient_descent(X,Y,theta)

好吧，太好了，這樣就行了！現(xiàn)在讓我們看看結(jié)果：

cost_function(X,y,sdg_thetas)

OUT:
29.833230764634493

哇！我們從592到29，但是請(qǐng)注意：我們只進(jìn)行了30次迭代。批量梯度下降，500次迭代后得到27次！這只是對(duì)隨機(jī)梯度下降的非凡力量的一瞥。

讓我們用一個(gè)圖再次將其可視化：

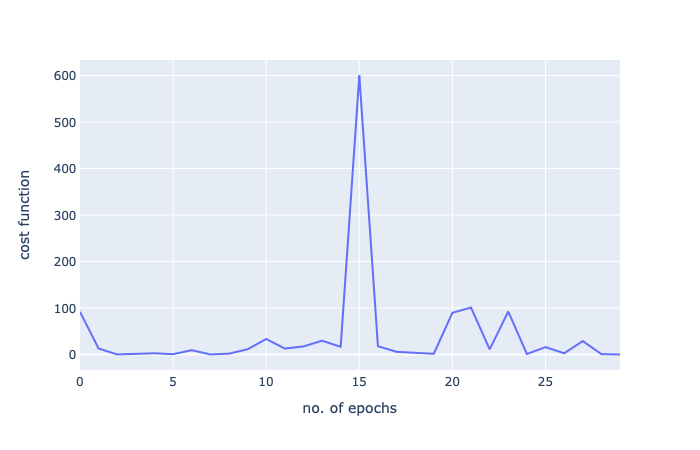
由于這是一個(gè)小數(shù)據(jù)集，批量梯度下降就足夠了，但這只是顯示了隨機(jī)梯度下降的力量。

優(yōu)點(diǎn)：

1. 與批量梯度下降相比更快

2. 更好地處理更大的數(shù)據(jù)集

缺點(diǎn)：

1. 在某個(gè)最小值上很難跳出

2. 并不總是有一個(gè)清晰的圖，可以在一個(gè)最小值附近反彈，但永遠(yuǎn)不會(huì)達(dá)到最佳的最小值

小批量梯度下降

好了，快到了，還有一個(gè)要通過！現(xiàn)在，在小批量梯度下降中，我們不再計(jì)算整個(gè)訓(xùn)練集或隨機(jī)樣本的偏導(dǎo)數(shù)，而是在整個(gè)訓(xùn)練集的小子集上計(jì)算。

這給了我們比批量梯度下降更快的速度，因?yàn)樗幌耠S機(jī)梯度下降那樣隨機(jī)，所以我們更接近于最小值。然而，它很容易陷入局部極小值。

同樣，為了解決陷入局部最小值的問題，我們將在實(shí)現(xiàn)中使用簡(jiǎn)易的學(xué)習(xí)率調(diào)整。

np.random.seed(42)?#?所以我們得到相同的結(jié)果

t0,?t1?=?200,?1000
def?learning_schedule(t):
????return?t0?/?(t?+?t1)
????
def?mini_batch_gradient_descent(X,y,thetas,n_iters=100,batch_size=20):
????t?=?0
????c_hist?=?[0]?*?n_iters
????for?epoch?in?range(n_iters):
????????shuffled_indices?=?np.random.permutation(len(y))
????????X_shuffled?=?X_scaled[shuffled_indices]
????????y_shuffled?=?y[shuffled_indices]
????????
????????for?i?in?range(0,len(Y),batch_size):
????????????t+=1
????????????xi?=?X_shuffled[i:i+batch_size]
????????????yi?=?y_shuffled[i:i+batch_size]
????????????
????????????gradient?=?2/batch_size?*?xi.T.dot(xi.dot(thetas)?-?yi)
????????????eta?=?learning_schedule(t)
????????????thetas?=?thetas?-?eta?*?gradient
????????????c_hist[epoch]?=?cost_function(xi,yi,thetas)
????return?thetas,c_hist

讓我們運(yùn)行并獲得結(jié)果：

mini_batch_gd_thetas,mini_batch_gd_cost?=?mini_batch_gradient_descent(X,y,theta)

以及新參數(shù)下的成本函數(shù)：

cost_function(X,Y,mini_batch_gd_thetas)

OUT:?27.509689139167012

又一次真的很棒。我們運(yùn)行了1/5的迭代，我們得到了一個(gè)更好的分?jǐn)?shù)！

讓我們?cè)佼嫵龊瘮?shù)：

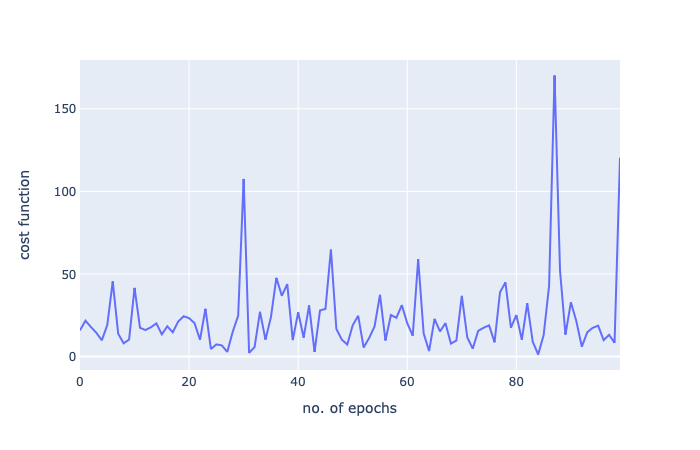
好了，我的梯度下降系列到此結(jié)束！感謝閱讀！