NeurIPS 2019杰出論文深度解讀:窺視機(jī)器學(xué)習(xí)的核心問題

??新智元推薦??

來源：學(xué)術(shù)頭條（ID：SciTouTiao）

作者：AMiner編輯部

【新智元導(dǎo)讀】在NeurIPS 2019一千多篇入選論文中，有那么1篇杰出論文值得長時(shí)間、深入、反復(fù)學(xué)習(xí)。這篇杰出論文的出彩之處在哪里呢？我們又能從中學(xué)到什么呢？現(xiàn)在戳右邊鏈接上新智元小程序??了解更多！

該論文的作者是：Ilias Diakonikolas（威斯康辛大學(xué)麥迪遜分校）、Themis Gouleakis（馬克斯普朗克計(jì)算機(jī)科學(xué)研究所）、Christos Tzamos（威斯康辛大學(xué)麥迪遜分校）。

論文地址：https://papers.nips.cc/paper/8722-distribution-independent-pac-learning-of- halfspaces-with-massart-noise

前言

本文將對(duì)NeurIPS 2019杰出論文《Distribution-Independent PAC Learning of Halfspaces with Massart Noise》進(jìn)行解讀，該論文在半空間學(xué)習(xí)上取得了顯著進(jìn)展。作者研究了存在Massart噪聲的半空間（halfspaces）分布獨(dú)立的PAC學(xué)習(xí)問題。具體而言，給定從R^d+1上的分布D中提取的一組有標(biāo)簽樣本(x, y)，使無標(biāo)記點(diǎn)x上的邊緣分布是任意的，且標(biāo)簽y由未知半空間生成，該空間被噪聲率為η＜1/2的Massart噪聲破壞。最終目標(biāo)是找到一個(gè)分類器h，使錯(cuò)誤分類誤差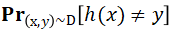最小。對(duì)于具有錯(cuò)誤分類誤差η+ε的問題，作者給出了一個(gè)poly(d, 1/ε)時(shí)間算法。作者還證明了對(duì)算法的誤差保證進(jìn)行改進(jìn)可能很難實(shí)現(xiàn)。在此工作之前，即使是析取類，在這個(gè)模型中也沒有有效的弱學(xué)習(xí)方法（分布獨(dú)立）。

研究現(xiàn)狀

Massart 噪聲與RCN

隨機(jī)分類噪聲（Random Classification Noise ，RCN）【1】是Massart噪聲的特殊情況，其每個(gè)標(biāo)簽的翻轉(zhuǎn)概率恰好為η＜1/2。似乎Massart噪聲比RCN更易于處理。但實(shí)際上，Massart對(duì)抗需要選擇是否擾動(dòng)給定的標(biāo)簽，如擾動(dòng)，以何種概率進(jìn)行，因此，在該模型中設(shè)計(jì)有效的算法具有很大挑戰(zhàn)性。尤其是，RCN學(xué)習(xí)與統(tǒng)計(jì)查詢（Statistical Query，SQ）模型【2】【3】之間的聯(lián)系不再成立，即，作為SQ算法的性質(zhì)已不能自動(dòng)滿足用Massart噪聲進(jìn)行噪聲容忍學(xué)習(xí)（noise-tolerant learning）的需要。而【4】【5】中正是利用了RCN與SQ模型的關(guān)系，得到了用RCN學(xué)習(xí)半空間的多項(xiàng)式時(shí)間算法。

相關(guān)工作介紹

Bylander【6】給出了多項(xiàng)式時(shí)間算法來學(xué)習(xí)帶有RCN的大邊界半空間（large margin halfspaces）（在附加的反集中假設(shè)下）。布魯姆等人【7】給出了第一個(gè)多項(xiàng)式時(shí)間算法，用于在無任何邊界假設(shè)情況下使用RCN對(duì)半空間進(jìn)行與分布獨(dú)立的學(xué)習(xí)。此后不久，Cohen【8】針對(duì)該問題給出了多項(xiàng)式時(shí)間適當(dāng)?shù)膶W(xué)習(xí)算法。隨后，Dunagan和Vempala【9】提出了一種重縮放的感知器算法，用于求解線性規(guī)劃，從而轉(zhuǎn)化為更簡單和快速的適當(dāng)學(xué)習(xí)算法。

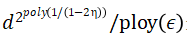在這項(xiàng)工作之前，在分布獨(dú)立的Massart噪聲模型中，基本上沒有具有非平凡誤差保證的有效算法。應(yīng)該注意的是，當(dāng)未標(biāo)記數(shù)據(jù)上的邊界分布在單位球面上時(shí)，具有誤差OPT +ε的多項(xiàng)式時(shí)間算法是已知的【10】【11】【12】。對(duì)于未標(biāo)記數(shù)據(jù)來自各向同性對(duì)數(shù)凹分布的情況，【13】給出了采樣和時(shí)間算法。

方法

相關(guān)基礎(chǔ)

帶Massart噪聲的半空間學(xué)習(xí)算法

學(xué)習(xí)大邊界半空間

一般情況

主要結(jié)果

作者主要結(jié)果是以下定理：

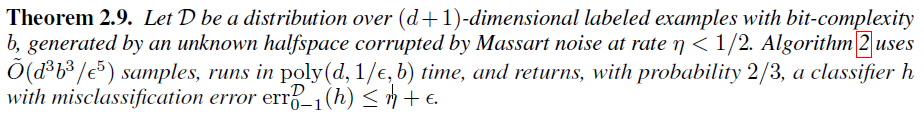
令D為（d + 1）維度的帶標(biāo)簽樣本在b-bit復(fù)雜度上的分布，由一個(gè)未知的半空間所產(chǎn)生，該空間被噪聲率為η＜1/2的Massart噪聲破壞。算法2使用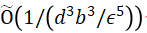個(gè)樣本，運(yùn)行時(shí)間為poly(d, 1/ε,?b)，最終以2/3的概率返回一個(gè)分類器h，且其誤分類誤差。

總結(jié)

作者提出了首個(gè)在帶Massart噪聲的半空間（halfspaces）的分布獨(dú)立的PAC學(xué)習(xí)的方法，即對(duì)具有錯(cuò)誤分類誤差η+ε的問題，給出了一個(gè)poly(d, 1/ε)時(shí)間算法。作者還證明對(duì)算法的錯(cuò)誤保證而進(jìn)行的改進(jìn)可能很難實(shí)現(xiàn)。

參考文獻(xiàn)：
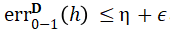【1】D. Angluin and P. Laird. Learning from noisy examples. Mach. Learn., 2(4):343–370,1988.【2】M. J. Kearns. Efficient noise-tolerant learning from statistical queries. In Proceedings of the Twenty-Fifth Annual ACM Symposium on Theory of Computing, pages 392–401,1993.【3】M. J. Kearns. Efficient noise-tolerant learning from statistical queries. Journal of the ACM, 45(6):983–1006, 1998.【4】A. Blum, A. M. Frieze, R. Kannan, and S. Vempala. A polynomial-time algorithm for learning noisy linear threshold functions. In 37th Annual Symposium on Foundations of Computer Science, FOCS ’96, pages 330–338, 1996.【5】A. Blum, A. Frieze, R. Kannan, and S. Vempala. A polynomial time algorithm for learning noisy linear threshold functions. Algorithmica, 22(1/2):35–52, 1997.【6】T. Bylander. Learning linear threshold functions in the presence of classification noise.In Proceedings of the Seventh Annual ACM Conference on Computational Learning Theory, COLT 1994, pages 340–347, 1994.【7】A. Blum, A. M. Frieze, R. Kannan, and S. Vempala. A polynomial-time algorithm for learning noisy linear threshold functions. In 37th Annual Symposium on Foundations of Computer Science, FOCS ’96, pages 330–338, 1996.【8】E. Cohen. Learning noisy perceptrons by a perceptron in polynomial time. In Proceedings of the Thirty-Eighth Symposium on Foundations of Computer Science, pages 514–521,1997.【9】J. Dunagan and S. Vempala. A simple polynomial-time rescaling algorithm for solving linear programs. In Proceedings of the 36th Annual ACM Symposium on Theory of Computing, pages 315–320, 2004【10】P. Awasthi, M. F. Balcan, N. Haghtalab, and R. Urner. Efficient learning of linear separators under bounded noise. In Proceedings of The 28th Conference on Learning Theory, COLT 2015, pages 167–190, 2015.【11】Y. Zhang, P. Liang, and M. Charikar. A hitting time analysis of stochastic gradient langevin dynamics. In Proceedings of the 30th Conference on Learning Theory, COLT 2017, pages 1980–2022, 2017.【12】Y. Zhang, P. Liang, and M. Charikar. A hitting time analysis of stochastic gradient langevin dynamics. In Proceedings of the 30th Conference on Learning Theory, COLT 2017, pages 1980–2022, 2017.【13】P. Awasthi, M. F. Balcan, N. Haghtalab, and H. Zhang. Learning and 1-bit compressed sensing under asymmetric noise. In Proceedings of the 29th Conference on Learning Theory, COLT 2016, pages 152–192, 2016.【14】A. Dvoretzky, J. Kiefer, and J. Wolfowitz. Asymptotic minimax character of the sample distribution function and of the classical multinomial estimator. Ann. Mathematical Statistics, 27(3):642–669, 1956.【15】J. Dunagan and S. Vempala. Optimal outlier removal in high-dimensional spaces. J.Computer & System Sciences, 68(2):335–373, 2004.
本文經(jīng)授權(quán)轉(zhuǎn)載自：學(xué)術(shù)頭條