【論文解讀】解讀TRPO論文,深度強(qiáng)化學(xué)習(xí)結(jié)合傳統(tǒng)優(yōu)化方法

導(dǎo)讀:本論文由Berkeley 的幾位大神于2015年發(fā)表于 JMLR(Journal of Machine Learning Research)。深度強(qiáng)化學(xué)習(xí)算法例如DQN或者PG(Policy Gradient)都無法避免訓(xùn)練不穩(wěn)定的問題:在訓(xùn)練過程中效果容易退化并且很難恢復(fù)。針對(duì)這個(gè)通病,TRPO采用了傳統(tǒng)優(yōu)化算法中的trust region方法,以保證每一步迭代能夠獲得效果提升,直至收斂到局部最優(yōu)點(diǎn)。
本篇論文涉及到的知識(shí)點(diǎn)比較多,不僅建立在強(qiáng)化學(xué)習(xí)領(lǐng)域經(jīng)典論文的結(jié)論:Kakade & Langford 于2002 年發(fā)表的 Approximately Optimal Approximate Reinforcement Learning 關(guān)于優(yōu)化目標(biāo)的近似目標(biāo)和重要性采樣,也涉及到傳統(tǒng)優(yōu)化方法 trust region 的建模和其具體的矩陣近似數(shù)值算法。讀懂本論文,對(duì)于深度強(qiáng)化學(xué)習(xí)及其優(yōu)化方法可以有比較深入的理解。本論文附錄的證明部分由于更為深?yuàn)W和冗長,在本文中不做具體講解,但是也建議大家能夠仔細(xì)研讀。
閱讀本論文需要注意的是,這里解讀的版本是arxiv的版本,這個(gè)版本帶有附錄,不同于 JMLR的版本的是,arxiv版本中用reward函數(shù)而后者用cost函數(shù),優(yōu)化方向相反。
arxiv 下載鏈接為 https://arxiv.org/pdf/1502.05477.pdf
0. 論文框架
本論文解決的目標(biāo)是希望每次迭代參數(shù)能保證提升效果,具體想法是利用優(yōu)化領(lǐng)域的 trust region方法(中文可以翻譯成置信域方法或信賴域方法),通過參數(shù)在trust region范圍中去找到一定能提升的下一次迭代。
本論文框架如下
首先,引入Kakade & Langford 論文 Approximately Optimal Approximate Reinforcement Learning 中關(guān)于近似優(yōu)化目標(biāo)的結(jié)論。(論文第二部分)
基于 Kakade 論文中使用mixture policy保證每一步效果提升的方法,擴(kuò)展到一般隨機(jī)策略,引入策略分布的total variation divergence作為約束。(論文第三部分)
將total variation divergence約束替換成平均 KL divergence 約束,便于使用蒙特卡洛方法通過采樣來生成每一步的具體優(yōu)化問題。(論文第四,五部分)
給出解決優(yōu)化問題的具體算法,將優(yōu)化目標(biāo)用first order來近似,約束項(xiàng)用second order 來近似,由于second order涉及到構(gòu)造Hessian matrix,計(jì)算量巨大,論文給出了 conjugate gradient + Fisher information matrix的近似快速實(shí)現(xiàn)方案。(論文第六部分)
從理論角度指出,Kakade 在2002年提出的方法natrual policy gradient 和經(jīng)典的policy gradient 都是TRPO的特別形式。(論文第七部分)
評(píng)價(jià)TRPO在兩種強(qiáng)化學(xué)習(xí)模式下的最終效果,一種是MuJoCo模擬器中能得到真實(shí)狀態(tài)的模式,一種是Atari游戲環(huán)境,即觀察到的屏幕像素可以信息完全地表達(dá)潛在真實(shí)狀態(tài)的模式。(論文第八部分)
本文下面的小結(jié)序號(hào)和論文小結(jié)序號(hào)相同,便于對(duì)照查閱。
1. 介紹
TRPO 第一次證明了最小化某種 surrogate 目標(biāo)函數(shù)且采用non-trivial的步長,一定可以保證策略提升。進(jìn)一步將此 surrogate 目標(biāo)函數(shù)轉(zhuǎn)換成trust region約束下的優(yōu)化問題。TRPO是一種on-policy 的算法,因?yàn)槊恳徊降枰谛碌牟呗韵峦ㄟ^采樣數(shù)據(jù)來構(gòu)建具體優(yōu)化問題。
2. 已有理論基礎(chǔ)
第二部分主要回顧了 Kakade & Langford 于2002 年的論文 Approximately Optimal Approximate Reinforcement Learning 中的一系列結(jié)論。
先來定義幾個(gè)重要概念的數(shù)學(xué)定義
是策略 的目標(biāo),即discounted reward 和的期望。

然后是策略的Q值和V值
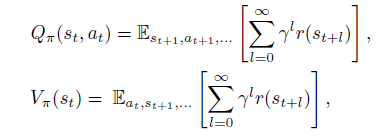
最后是策略的advantage函數(shù)
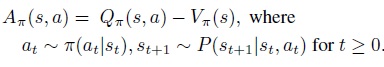
接著,開始引入 Kakade & Langford 論文結(jié)論,即下式(公式1)。
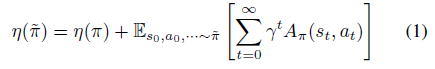
公式1表明,下一次迭代策略的目標(biāo)可以分解成現(xiàn)有策略的目標(biāo) 和現(xiàn)有advantage 函數(shù)在新策略trajectory分布下的期望。
公式1可以很容易從trajectory分布轉(zhuǎn)換成新策略在狀態(tài)的訪問頻率,即公式2
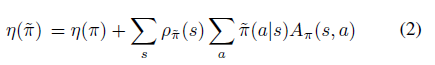
狀態(tài)的訪問頻率或穩(wěn)定狀態(tài)分布定義成
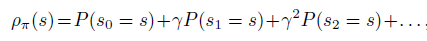 ?
?注意到公式2中狀態(tài)的期望依然依賴于新策略 的穩(wěn)定狀態(tài)分布,不方便實(shí)現(xiàn)。原因如下,期望形式有利于采樣來解決問題,但是由于采樣數(shù)據(jù)源于 on-policy 而非 ,因此無法直接采樣未知的策略 ?。
幸好,Kakade 論文中證明了,可以用 的代替 ?并且證明了這種代替下的近似目標(biāo)函數(shù) 是原來函數(shù)的一階近似
即滿足
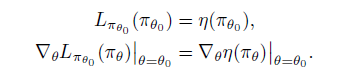 ?
?具體定義表達(dá)式為
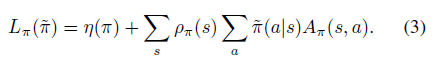 ?
?是一階近似意味著在小范圍區(qū)域中一定是可以得到提升的,但是范圍是多大,是否能保證 的提升?Kakade的論文中不僅給出了通過mix新老策略的提升方式,還給出了這個(gè)方式對(duì)原目標(biāo) 較 的提升下屆。
策略更新規(guī)則如下
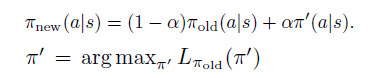 ?
?公式6為具體提升下屆為
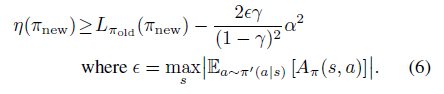 ?
?3. 擴(kuò)展到隨機(jī)策略
論文的這一部分將Kakade的mix policy update 擴(kuò)展到一般的隨機(jī)策略,同時(shí)依然保證每次迭代能得到目標(biāo)提升。
首先,每次策略迭代必須不能和現(xiàn)有策略變化太大,因此,引入分布間常見的TV divergence,即 total variation divergence。
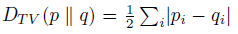 ?
?有了兩個(gè)分布距離的定義,就可以定義兩個(gè)策略的距離。離散狀態(tài)下,一個(gè)策略是狀態(tài)到動(dòng)作分布的 map 或者 dict,因此,可以定義兩個(gè)策略的距離為所有狀態(tài)中最大的動(dòng)作分布的 ,即
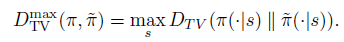 ?
?至此,可以引出定理一:在一般隨機(jī)策略下,Kakade 的surrogate函數(shù)較原目標(biāo)的提升下屆依然成立,即公式8在新的定義下可以從公示6推導(dǎo)而來。
 ?
?進(jìn)一步將 TV divergence 轉(zhuǎn)換成 KL divergence,轉(zhuǎn)換成KL divergence 的目的是為了后續(xù)使用傳統(tǒng)且成熟的 trust region 蒙特卡洛方法和 conjugate gradient 的優(yōu)化近似解法。
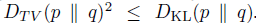 ?
?由于上面兩種距離的大小關(guān)系,可以推導(dǎo)出用KL divergence表示的 較 的提升下屆
 ?
?根據(jù)公式9,就可以形成初步的概念上的算法一,通過每一步形成無約束優(yōu)化問題,同時(shí)保證每次迭代的 對(duì)應(yīng)的 是遞增的。
 ?
?4. Trust Region Policy Optimization
看到這里已經(jīng)不容易了,盡管算法一給出了一個(gè)解決方案,但是本論文的主角TRPO 還未登場。TRPO算法的作用依然是近似!
算法一對(duì)于下面的目標(biāo)函數(shù)做優(yōu)化,即每次找到下一個(gè) 最大化下式, 每一步一定能得到提升。
問題是在實(shí)踐中,懲罰系數(shù) 會(huì)導(dǎo)致步長非常小,一種穩(wěn)定的使用較大步長的方法是將懲罰項(xiàng)變成約束項(xiàng),即:
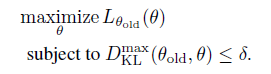 ?
?將 放入約束項(xiàng)中符合trust region 這種傳統(tǒng)優(yōu)化解法。
關(guān)于 約束,再補(bǔ)充兩點(diǎn)
的定義是兩個(gè)策略中所有狀態(tài)中最大的動(dòng)作分布的 ,因此它約束了所有狀態(tài)下新老策略動(dòng)作分布的KL散度,也就意味著有和狀態(tài)數(shù)目相同數(shù)量的約束項(xiàng),海量的約束項(xiàng)導(dǎo)致算法很難應(yīng)用到實(shí)際中。
約束項(xiàng)的 trust region 不是參數(shù) 的空間,而是其KL散度的空間。
基于第一點(diǎn),再次使用近似法,在約束項(xiàng)中用KL期望 來代替各個(gè)狀態(tài)下的KL散度,權(quán)重為on-policy 策略的分布
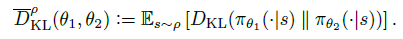 ?
?最終,得到TRPO在實(shí)際中的優(yōu)化目標(biāo)(12式):
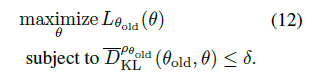 ?
?5. 用采樣方法來Trust Region約束優(yōu)化
論文第五部分,將TRPO優(yōu)化目標(biāo)12式改寫成期望形式,引入兩種蒙特卡洛方法 single path 和 vine 來采樣。
具體來說, 由兩項(xiàng)組成
第一項(xiàng)是常量,只需優(yōu)化第二項(xiàng),即優(yōu)化問題等價(jià)為13式
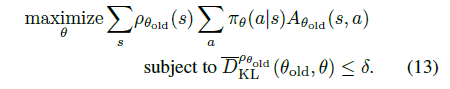 ?
?隨后,為了可以適用非 on-policy 的動(dòng)作分布來任意采樣,引入采樣的動(dòng)作分布 ,將13式中的 部分通過重要性采樣改成以下形式:
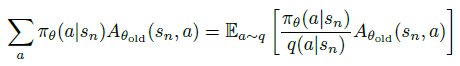 ?
?再將13式中的 改成期望形式 ,并將 改成 值,得14式。
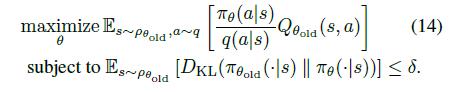 ?
?至此,我們得到trust region優(yōu)化的期望形式:優(yōu)化目標(biāo)中期望的狀態(tài)空間是基于 on-policy ,動(dòng)作空間是基于任意采樣分布 ,優(yōu)化約束中的期望是基于 on-policy 。
5.1 Single path采樣
根據(jù)14式,single path 是最基本的的蒙特卡洛采樣方法,和REINFORCE算法一樣, 通過on-policy 生成采樣的 trajectory數(shù)據(jù):,然后代入14式。注意,此時(shí) ,即用現(xiàn)有策略的動(dòng)作分布直接代替采樣分布。
 ?
?5.2 Vine 采樣
雖然single path方法簡單明了,但是有著online monte carlo方法固有的缺陷,即variance較大。Vine方法通過在一個(gè)狀態(tài)多次采樣來改善此缺陷。Vine的翻譯是藤,寓意從一個(gè)狀態(tài)多次出發(fā)來采樣,如下圖, 狀態(tài)下采樣多個(gè)rollouts,很像植物的藤長出多分叉。當(dāng)然,vine方法要求環(huán)境能restart 到某一狀態(tài),比如游戲環(huán)境通過save load返回先前的狀態(tài)。
 ?
?具體來說,vine 方法首先通過生成多個(gè)on-policy 的trajectories來確定一個(gè)狀態(tài)集合 。對(duì)于狀態(tài)集合的每一個(gè)狀態(tài) 采樣K個(gè)動(dòng)作,服從 。接著,對(duì)于每一個(gè) 再去生成一次 rollout 來估計(jì) 。試驗(yàn)證明,在連續(xù)動(dòng)作空間問題中, 直接使用 on-policy 可以取得不錯(cuò)效果,在離散空間問題中,使用uniform分布效果更好。
6. 轉(zhuǎn)換成具體優(yōu)化問題
再回顧一下現(xiàn)在的進(jìn)度,12式定義了優(yōu)化目標(biāo),約束項(xiàng)是KL divergence空間的trust region 形式。14式改寫成了等價(jià)的期望形式,通過兩種蒙特卡洛方法生成 state-action 數(shù)據(jù)集,可以代入14式得到每一步的具體數(shù)值的優(yōu)化問題。論文這一部分簡單敘述了如何高效但近似的解此類問題,詳細(xì)的一些步驟在附錄中闡述。我們把相關(guān)解讀都放在下一節(jié)。
7. 和已有理論的聯(lián)系
7.1 簡化成 Natural Policy Gradient
再回到12式,即約束項(xiàng)是KL divergence空間的trust region 形式
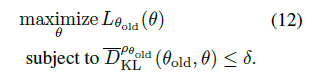 ?
?對(duì)于這種形式的優(yōu)化問題,一般的做法是通過對(duì)優(yōu)化目標(biāo)做一階函數(shù)近似,即
并對(duì)約束函數(shù)做二階函數(shù)近似,因?yàn)榧s束函數(shù)在 點(diǎn)取到極值,因此一階導(dǎo)為0。
12式的優(yōu)化目標(biāo)可以轉(zhuǎn)換成17式
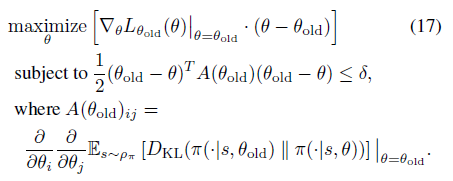 ?
?對(duì)應(yīng)參數(shù)迭代更新公式如下
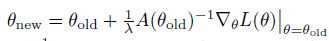 ?
?這個(gè)方法便是Kakade在2002年發(fā)表的 natrual policy gradient 論文。
7.2 簡化成 Policy Gradient
注意,的一階近似的梯度
即PG定理
因此,PG定理等價(jià)于的一階近似的梯度在 空間 約束下的優(yōu)化問題,即18式
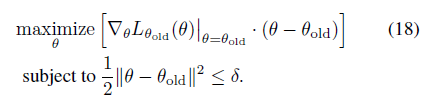 ?
?7.3 近似數(shù)值解法
這里簡單描述關(guān)于17式及其參數(shù)更新規(guī)則中的大矩陣數(shù)值計(jì)算近似方式。
二階近似中的 是 Hessian 方形矩陣,維度為 個(gè)數(shù)的平方。
 ?
?直接構(gòu)建 矩陣或者其逆矩陣 都是計(jì)算量巨大的, 注出現(xiàn)在natural policy update 更新公式中, 。
一種方法是通過構(gòu)建Fisher Information Matrix,引入期望形式便于采樣
另一種方式是使用conjugate gradient 方法,通過矩陣乘以向量快速計(jì)算法迭代逼近 。
8. 試驗(yàn)結(jié)果
在兩種強(qiáng)化學(xué)習(xí)模式下,比較TRPO和其他模型的效果。模式一是在MuJoCo模擬器中,這種環(huán)境下能得到真實(shí)狀態(tài)的情況。
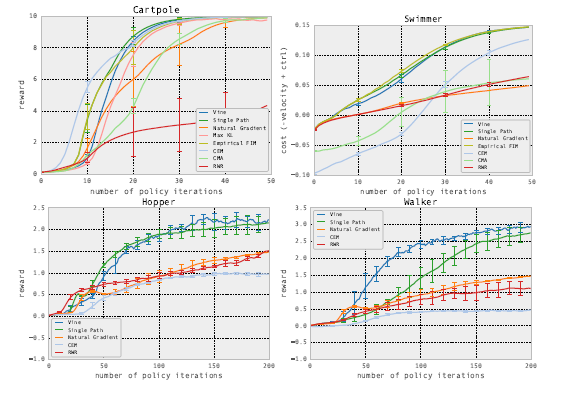 ?
?另一種模式是完全信息下的Atari游戲環(huán)境,這種環(huán)境下觀察到的屏幕像素可以信息完全地表達(dá)潛在真實(shí)狀態(tài)。
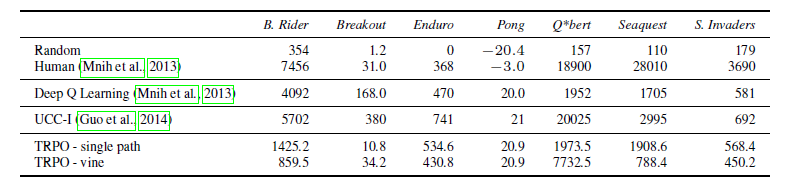 ?
?往期精彩回顧
獲取本站知識(shí)星球優(yōu)惠券,復(fù)制鏈接直接打開:
https://t.zsxq.com/qFiUFMV
本站qq群704220115。
加入微信群請掃碼:
