機器學(xué)習(xí)基礎(chǔ):樸素貝葉斯及經(jīng)典實例講解
點擊上方“小白學(xué)視覺”,選擇加"星標(biāo)"或“置頂”
重磅干貨,第一時間送達(dá)
原文連接:?
https://www.cnblogs.com/lliuye/p/9178090.htmlhttps://www.cnblogs.com/huangyc/p/10327209.html
樸素貝葉斯法(Naive Bayes)是基于貝葉斯定理與特征條件獨立假設(shè)的分類方法。對于給定的訓(xùn)練數(shù)據(jù)集,首先基于特征條件獨立假設(shè)學(xué)習(xí)輸入/輸出的聯(lián)合概率分布;然后基于此模型,對給定的輸入 x ,利用貝葉斯定理求出后驗概率最大的輸出 y ,即為對應(yīng)的類別。
在夏季,某公園男性穿涼鞋的概率為 1/2 ,女性穿涼鞋的概率為 2/3 ,并且該公園中男女比例通常為 2:1 ,問題:若你在公園中隨機遇到一個穿涼鞋的人,請問他的性別為男性或女性的概率分別為多少?
先驗概率
我們使用以上例子來解釋一下什么是先驗概率。根據(jù)以上例子我們設(shè)定:假設(shè)某公園中一個人是男性為事件 Y=ymen ,是女性則是 Y=ywomen ;一個人穿涼鞋為事件 X=x1 ,未穿涼鞋為事件 X=x0 。而一個人的性別與是否穿涼鞋這兩個事件之間是相互獨立的。于是我們可以看到該例子中存在四個先驗概率:
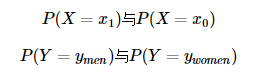
由于男女生的比例是2:1,那么P(Y=ymen)自然等于2/3,P(Y=ywomen)同理。而先驗概率 P(Y=ymen)與P(Y=ywomen) 并不能直接得出,需要根據(jù)全概率公式來求解。在學(xué)習(xí)全概率公式之前,我們先了解一下條件概率。
條件概率
條件概率是指在事件 Y=y 已經(jīng)發(fā)生的條件下,事件 X=x 發(fā)生的概率。條件概率可表示為:P(X=x|Y=y) 。而條件概率計算公式為:
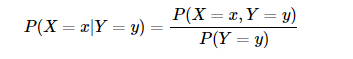
其中 P(X=x,Y=y) 是聯(lián)合概率,也就是兩個事件共同發(fā)生的概率。而 P(Y=y)以及P(X=x) 是先驗概率。我們用例子來說明一下就是:“某公園男性穿涼鞋的概率為 1/2 ”,也就是說“是男性的前提下,穿涼鞋的概率是 1/2 ”,此概率為條件概率,即 P(X=x1|Y=ymen)=1/2 。同理“女性穿涼鞋的概率為 2/3 ” 為條件概率 P(X=x1|Y=ywomen)=1/2 。
全概率公式是指:如果事件 Y=y1,Y=y2,...,Y=yn 可構(gòu)成一個完備事件組,即它們兩兩互不相容,其和為全集。則對于事件 X=x 有:
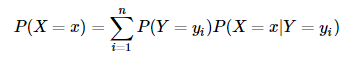
因此對于上面的例子,我們可以根據(jù)全概率公式求得:
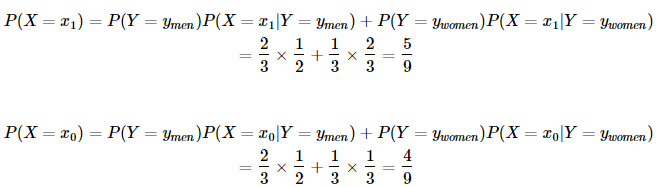
也就是說不考慮性別的情況下,公園中穿拖鞋的概率為 5/9 ,不穿拖鞋的概率為 4/9 。
后驗概率
后驗概率是指,某事件 X=x 已經(jīng)發(fā)生,那么該事件是因為事件 Y=y 的而發(fā)生的概率。也就是上例中所需要求解的“在知道一個人穿拖鞋的前提下,這個人是男性的概率或者是女性的概率是多少”。后驗概率形式化便是:
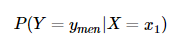
后驗概率的計算要以先驗概率為基礎(chǔ)。后驗概率可以根據(jù)通過貝葉斯公式,用先驗概率和似然函數(shù)計算出來。
貝葉斯公式如下:
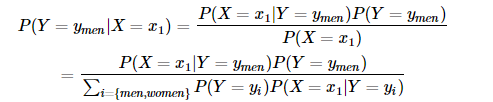
說明:分母的變形是使用全概率公式,Y事件取值范圍為:{men, women},即男生和女生;分子的變現(xiàn)是根據(jù)獨立條件概率(貝葉斯定理):
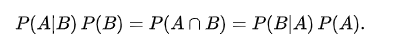
兩邊同時除以P(B)得到,上節(jié)有證明?貝葉斯定理的通俗理解。
根據(jù)前面的約定,X=x1表示穿穿拖鞋,Y=ymen?表示男生,該公式即為,穿拖鞋情況下,是男生的概率,正式題目需要我們求的。
而樸素貝葉斯算法正是利用以上信息求解后驗概率,并依據(jù)后驗概率的值來進(jìn)行分類。使用上面的例子來進(jìn)行理解,將先驗概率和條件概率帶入得,后驗概率為:
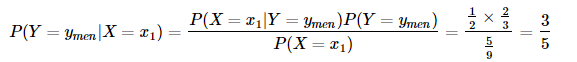
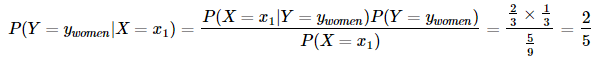
即,在x1(一個人穿拖鞋的情況下),是男生概率是3/5,是女生的概率為2/5,那么,對于分類情況,作為單選題的話,我們有理由將這個人歸類為男性,因為是男性的概率大些。
樸素貝葉斯
對于樣本集:
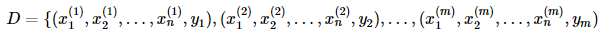
其中 m 表示有 m 個樣本, n 表示有 n 個特征。yi,i=1,2,..,m 表示樣本類別,取值為 {C1,C2,...,CK} 。
(怎么理解呢,yi?我們可以理解為前例的男生,女生,特征可以看成,穿拖鞋)
樸素貝葉斯分類的基本公式
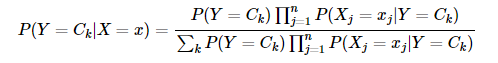
化簡一下,樸素貝葉斯分類器可表示為:
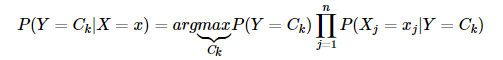
樸素貝葉斯算法過程
1)計算先驗概率:求出樣本類別的個數(shù) K 。對于每一個樣本 Y=Ck ,計算出 P(Y=Ck) 。其為類別 Ck 在總樣本集中的頻率(對于前例男生女生,k=2,男生概率,女生概率)。
2)計算條件概率:將樣本集劃分成 K 個子樣本集,分別對屬于 Ck 的子樣本集進(jìn)行計算,計算出其中特征 Xj=ajl 的概率:P(Xj=ajl|Y=Ck)。其為該子集中特征取值為 ajl 的樣本數(shù)與該子集樣本數(shù)的比值。(前例中,穿拖鞋與否就是一個特征,對于男生,需要計算穿拖鞋的條件概率,女生也一樣)
3)針對待預(yù)測樣本 xtest ,計算其對于每個類別 Ck 的后驗概率:
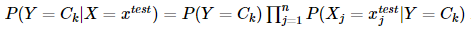
計算結(jié)果,概率值最大的類別即為待預(yù)測樣本的預(yù)測類別。(前例中,由于計算出來,男生概率大,對于分類問題,我們認(rèn)為是男生)
樸素貝葉斯算法分析
優(yōu)點:
(1)樸素貝葉斯模型發(fā)源于古典數(shù)學(xué)理論,有穩(wěn)定的分類效率。
(2)對小規(guī)模的數(shù)據(jù)表現(xiàn)很好,能個處理多分類任務(wù),適合增量式訓(xùn)練,尤其是數(shù)據(jù)量超出內(nèi)存時,我們可以一批批的去增量訓(xùn)練。
(3)對缺失數(shù)據(jù)不太敏感,算法也比較簡單,常用于文本分類。
缺點:
(1)理論上,樸素貝葉斯模型與其他分類方法相比具有最小的誤差率。但是實際上并非總是如此,這是因為樸素貝葉斯模型給定輸出類別的情況下,假設(shè)屬性之間相互獨立,這個假設(shè)在實際應(yīng)用中往往是不成立的,在屬性個數(shù)比較多或者屬性之間相關(guān)性較大時,分類效果不好。而在屬性相關(guān)性較小時,樸素貝葉斯性能最為良好。對于這一點,有半樸素貝葉斯之類的算法通過考慮部分關(guān)聯(lián)性適度改進(jìn)。
(2)需要知道先驗概率,且先驗概率很多時候取決于假設(shè),假設(shè)的模型可以有很多種,因此在某些時候會由于假設(shè)的先驗?zāi)P偷脑驅(qū)е骂A(yù)測效果不佳。
(3)由于我們是通過先驗和數(shù)據(jù)來決定后驗的概率從而決定分類,所以分類決策存在一定的錯誤率。
(4)對輸入數(shù)據(jù)的表達(dá)形式很敏感。
垃圾郵件分類實現(xiàn)
樸素貝葉斯 (naive Bayes) 法是基于貝葉斯定理與特征條件獨立假設(shè)的分類的方法。對于給定的訓(xùn)練數(shù)據(jù)集,首先基于特征條件獨立假設(shè)學(xué)習(xí)輸入/輸出的聯(lián)合概率分布;然后基于此模型,對于給定的輸入
輸入:
#垃圾郵件的內(nèi)容
posting_list = [
['my', 'dog', 'has', 'flea', 'problem', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'ny', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']
]
#是否是垃圾郵件的標(biāo)簽
labels = [0, 1, 0, 1, 0, 1]首先得根據(jù)上述文本建立一個詞匯表,即把重復(fù)的詞匯剔除。代碼如下:
def createVocabList(dataSet):
'''
創(chuàng)建所有文檔中出現(xiàn)的不重復(fù)詞匯列表
Args:
dataSet: 所有文檔
Return:
包含所有文檔的不重復(fù)詞列表,即詞匯表
'''
vocabSet = set([])
# 創(chuàng)建兩個集合的并集
for document in dataSet:
vocabSet = vocabSet | set(document)
return list(vocabSet)然后需要把每句話轉(zhuǎn)化為詞袋模型(bag-of-words model):
# 詞袋模型(bag-of-words model):詞在文檔中出現(xiàn)的次數(shù)
def bagOfWords2Vec(vocabList, inputSet):
'''
依據(jù)詞匯表,將輸入文本轉(zhuǎn)化成詞袋模型詞向量
Args:
vocabList: 詞匯表
inputSet: 當(dāng)前輸入文檔
Return:
returnVec: 轉(zhuǎn)換成詞向量的文檔
例子:
vocabList = ['I', 'love', 'python', 'and', 'machine', 'learning']
inputset = ['python', 'machine', 'learning', 'python', 'machine']
returnVec = [0, 0, 2, 0, 2, 1]
長度與詞匯表一樣長,出現(xiàn)了的位置為1,未出現(xiàn)為0,如果詞匯表中無該單詞則print
'''
returnVec = [0] * len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] += 1
else:
print("the word: %s is not in my vocabulary!" % word)
return returnVec目前為止,我們把每份郵件轉(zhuǎn)化成了一系列的向量形式,向量的長度是詞表里面的詞的個數(shù),是稀疏矩陣。
接下去就是樸素貝葉斯的步驟了,也就是訓(xùn)練的過程:
def fit(self, trainMatrix, trainCategory):
'''
樸素貝葉斯分類器訓(xùn)練函數(shù),求:p(Ci),基于詞匯表的p(w|Ci)
Args:
trainMatrix : 訓(xùn)練矩陣,即向量化表示后的文檔(詞條集合)
trainCategory : 文檔中每個詞條的列表標(biāo)注
Return:
p0Vect : 屬于0類別的概率向量(p(w1|C0),p(w2|C0),...,p(wn|C0))
p1Vect : 屬于1類別的概率向量(p(w1|C1),p(w2|C1),...,p(wn|C1))
pAbusive : 屬于1類別文檔的概率
'''
numTrainDocs = len(trainMatrix)
# 長度為詞匯表長度
numWords = len(trainMatrix[0])
# p(ci)
self.pAbusive = sum(trainCategory) / float(numTrainDocs)
# 由于后期要計算p(w|Ci)=p(w1|Ci)*p(w2|Ci)*...*p(wn|Ci),若wj未出現(xiàn),則p(wj|Ci)=0,因此p(w|Ci)=0,這樣顯然是不對的
# 故在初始化時,將所有詞的出現(xiàn)數(shù)初始化為1,分母即出現(xiàn)詞條總數(shù)初始化為2
p0Num = np.ones(numWords)
p1Num = np.ones(numWords)
p0Denom = 2.0
p1Denom = 2.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
# p(wi | c1)
# 為了避免下溢出(當(dāng)所有的p都很小時,再相乘會得到0.0,使用log則會避免得到0.0)
self.p1Vect = np.log(p1Num / p1Denom)
# p(wi | c2)
self.p0Vect = np.log(p0Num / p0Denom)
return self訓(xùn)練完了,剩下的是對新數(shù)據(jù)的預(yù)測過程:
def predict(self, testX):
'''
樸素貝葉斯分類器
Args:
testX : 待分類的文檔向量(已轉(zhuǎn)換成array)
p0Vect : p(w|C0)
p1Vect : p(w|C1)
pAbusive : p(C1)
Return:
1 : 為侮辱性文檔 (基于當(dāng)前文檔的p(w|C1)*p(C1)=log(基于當(dāng)前文檔的p(w|C1))+log(p(C1)))
0 : 非侮辱性文檔 (基于當(dāng)前文檔的p(w|C0)*p(C0)=log(基于當(dāng)前文檔的p(w|C0))+log(p(C0)))
'''
p1 = np.sum(testX * self.p1Vect) + np.log(self.pAbusive)
p0 = np.sum(testX * self.p0Vect) + np.log(1 - self.pAbusive)
if p1 > p0:
return 1
else:
return 0下載1:OpenCV-Contrib擴展模塊中文版教程 在「小白學(xué)視覺」公眾號后臺回復(fù):擴展模塊中文教程,即可下載全網(wǎng)第一份OpenCV擴展模塊教程中文版,涵蓋擴展模塊安裝、SFM算法、立體視覺、目標(biāo)跟蹤、生物視覺、超分辨率處理等二十多章內(nèi)容。 下載2:Python視覺實戰(zhàn)項目52講 在「小白學(xué)視覺」公眾號后臺回復(fù):Python視覺實戰(zhàn)項目,即可下載包括圖像分割、口罩檢測、車道線檢測、車輛計數(shù)、添加眼線、車牌識別、字符識別、情緒檢測、文本內(nèi)容提取、面部識別等31個視覺實戰(zhàn)項目,助力快速學(xué)校計算機視覺。 下載3:OpenCV實戰(zhàn)項目20講 在「小白學(xué)視覺」公眾號后臺回復(fù):OpenCV實戰(zhàn)項目20講,即可下載含有20個基于OpenCV實現(xiàn)20個實戰(zhàn)項目,實現(xiàn)OpenCV學(xué)習(xí)進(jìn)階。 交流群
歡迎加入公眾號讀者群一起和同行交流,目前有SLAM、三維視覺、傳感器、自動駕駛、計算攝影、檢測、分割、識別、醫(yī)學(xué)影像、GAN、算法競賽等微信群(以后會逐漸細(xì)分),請掃描下面微信號加群,備注:”昵稱+學(xué)校/公司+研究方向“,例如:”張三?+?上海交大?+?視覺SLAM“。請按照格式備注,否則不予通過。添加成功后會根據(jù)研究方向邀請進(jìn)入相關(guān)微信群。請勿在群內(nèi)發(fā)送廣告,否則會請出群,謝謝理解~

