青青草综合视频,成人三级久久久,黄色视频网站在线,无码翔田千里,国产精品无码天天爽视频,三级久久三级久久三级,久热国产在线,一区二区天堂

來源：碼海

作者：碼海

如果說數(shù)據(jù)結構是算法的基礎，那么數(shù)組和鏈表就是數(shù)據(jù)結構的基礎。因為像堆，棧，樹，圖等比較復雜的數(shù)組結基本上都可以由數(shù)組和鏈表來表示，所以掌握數(shù)組和鏈表的基本操作十分重要。

鏈表的知識點蠻多的，所以分成上下兩篇，這篇主要講解鏈表翻轉的解題技巧，下篇主要講關于鏈表快慢指針的知識點，干貨很多，建議先收藏再看。認真看完保證收獲滿滿！

今天就來看看鏈表的基本操作及其在面試中的常見解題思路,本文將從以下幾個點來講解鏈表的核心知識

什么是鏈表，鏈表的優(yōu)缺點
鏈表的表示及基本操作
面試中鏈表的常見解題思路---翻轉

什么是鏈表

相信大家已經(jīng)開始迫不及待地想用鏈表解題了，不過在開始之前我們還是要先來溫習下鏈表的定義，以及它的優(yōu)勢與劣勢，磨刀不誤砍柴功！

鏈表的定義

鏈表是物理存儲單元上非連續(xù)的、非順序的存儲結構，它是由一個個結點，通過指針來聯(lián)系起來的，其中每個結點包括數(shù)據(jù)和指針。

鏈表的非連續(xù)，非順序，對應數(shù)組的連續(xù)，順序，我們來看看整型數(shù)組 1，2，3，4 在內存中是如何表示的

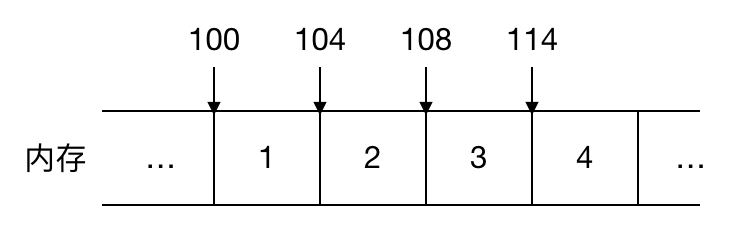可以看到數(shù)組的每個元素都是連續(xù)緊鄰分配的，這叫連續(xù)性，同時由于數(shù)組的元素占用的大小是一樣的，在 Java 中 int 型大小固定為 4 個字節(jié),所以如果數(shù)組的起始地址是 100，由于這些元素在內存中都是連續(xù)緊鄰分配的，大小也一樣，可以很容易地找出數(shù)組中任意一個元素的位置，比如數(shù)組中的第三個元素起始地址為 100 + 2 * 4 = 108,這就叫順序性。查找的時間復雜度是O(1),效率很高！

那鏈表在內存中是怎么表示的呢

可以看到每個結點都分配在非連續(xù)的位置，結點與結點之間通過指針連在了一起，所以如果我們要找比如值為 3 ?的結點時，只能通過結點 1 從頭到尾遍歷尋找，如果元素少還好，如果元素太多（比如超過一萬個），每個元素的查找都要從頭開始查找，時間復雜度是O(n)，比起數(shù)組的 O(1)，差距不小。

除了查找性能鏈表不如數(shù)組外，還有一個優(yōu)勢讓數(shù)組的性能高于鏈表,這里引入程序局部性原理，啥叫程序局部性原理。

我們知道 CPU 運行速度是非常快的，如果 CPU 每次運算都要到內存里去取數(shù)據(jù)無疑是很耗時的，所以在 CPU 與內存之間往往集成了挺多層級的緩存，這些緩存越接近CPU，速度越快，所以如果能提前把內存中的數(shù)據(jù)加載到如下圖中的 L1, L2, L3 緩存中，那么下一次 CPU 取數(shù)的話直接從這些緩存里取即可，能讓CPU執(zhí)行速度加快，那什么情況下內存中的數(shù)據(jù)會被提前加載到 L1,L2,L3 緩存中呢，答案是當某個元素被用到的時候，那么這個元素地址附近的的元素會被提前加載到緩存中

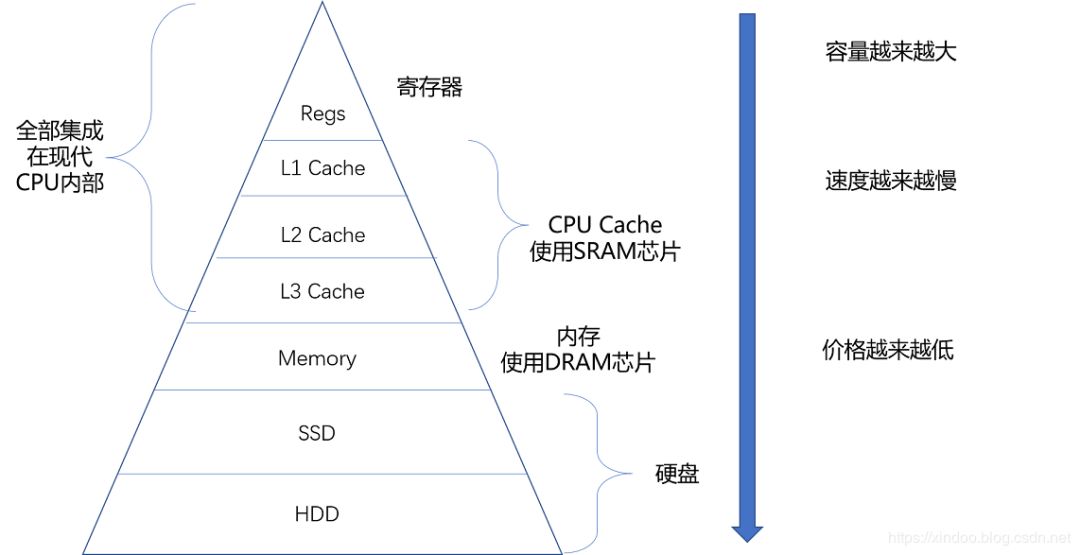
以上文整型數(shù)組 1，2，3，4為例，當程序用到了數(shù)組中的第一個元素（即 1）時，由于 CPU 認為既然 1 被用到了，那么緊鄰它的元素 2，3，4 被用到的概率會很大，所以會提前把 2，3，4 加到 L1,L2,L3 緩存中去，這樣 CPU 再次執(zhí)行的時候如果用到 2，3，4，直接從 L1,L2,L3 緩存里取就行了，能提升不少性能

畫外音：如果把 CPU 的一個時種看成一秒，則從 L1 讀取數(shù)據(jù)需要 3 秒，從 L2 讀取需要 11 秒，L3讀取需要 25秒，而從內存讀取呢，需要 1 分 40 秒，所以程序局部性原理能對 CPU 執(zhí)行性能有很大的提升

而鏈表呢，由于鏈表的每個結點在內存里都是隨機分布的，只是通過指針聯(lián)系在一起，所以這些結點的地址并不相鄰，自然無法利用 程序局部性原理 來提前加載到 L1,L2,L3 緩存中來提升程序性能。

畫外音：程序局部性原理是計算機中非常重要的原理，這里不做展開，建議大家查閱相關資料詳細了解一下

如上所述，相比數(shù)組，鏈表的非連續(xù)，非順序確實讓它在性能上處于劣勢，那什么情況下該使用鏈表呢？考慮以下情況

大內存空間分配

由于數(shù)組空間的連續(xù)性，如果要為數(shù)組分配 500M 的空間，這 500M 的空間必須是連續(xù)的，未使用的，所以在內存空間的分配上數(shù)組的要求會比較嚴格，如果內存碎片太多，分配連續(xù)的大空間很可能導致失敗。而鏈表由于是非連續(xù)的，所以這種情況下選擇鏈表更合適。

元素頻繁刪除和插入

如果涉及到元素的頻繁刪除和插入，用鏈表就會高效很多，對于數(shù)組來說，如果要在元素間插入一個元素，需要把其余元素一個個往后移（如圖示），以為新元素騰空間（同理，如果是刪除則需要把被刪除元素之后的元素一個個往前移），效率上無疑是比較低的。

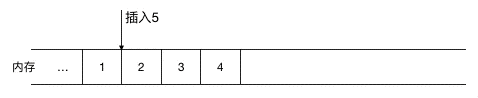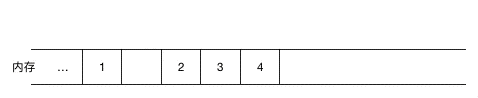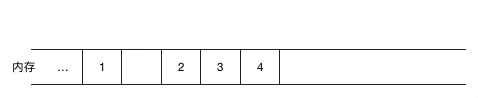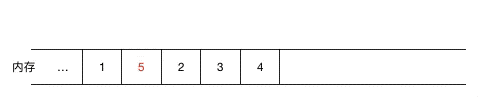(在 1，2 間插入 5，需要把2，3，4 同時往后移一位)

而鏈表的插入刪除相對來說就比較簡單了，修改指針位置即可，其他元素無需做任何移動操作（如圖示：以插入為例）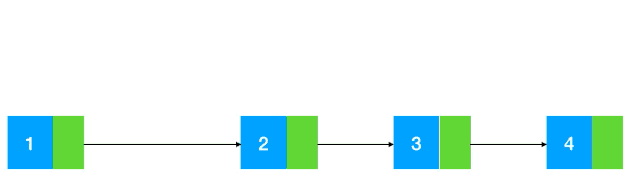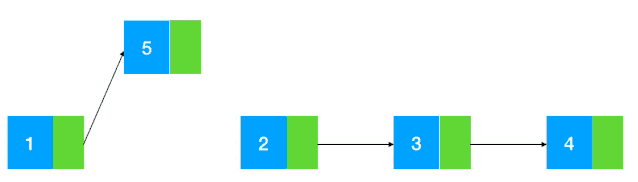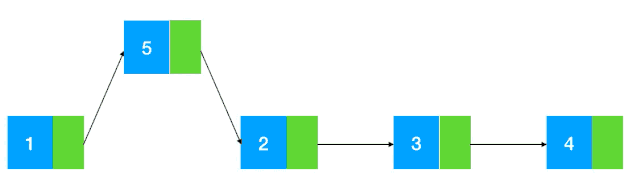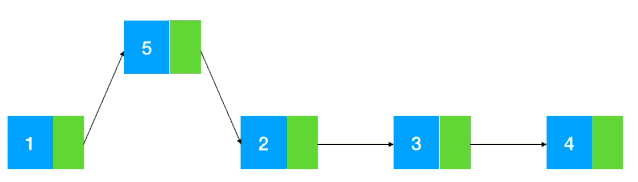

綜上所述：如果數(shù)據(jù)以查為主，很少涉及到增和刪，選擇數(shù)組，如果數(shù)據(jù)涉及到頻繁的插入和刪除，或元素所需分配空間過大，傾向于選擇鏈表。

說了這么多理論，相信讀者對數(shù)組和鏈表的區(qū)別應該有了更深刻地認識了，尤其是 程序局部性原理，是不是開了不少眼界^_^，如果面試中問到數(shù)組和鏈表的區(qū)別能回答到程序局部性原理，會是一個非常大的亮點！

接下來我們來看看鏈表的表現(xiàn)形式和解題技巧

需要說明的是有些代碼像打印鏈表等限于篇幅的關系沒有在文中展示，我把文中所有相關代碼都放到 github 中了，大家如果需要，可以訪問我的 github 地址: https://github.com/allentofight/algorithm 下載運行（微信不支持外鏈，建議大家 copy 之后瀏覽器打開再下載運行），文中所有代碼均已用 Java 實現(xiàn)并運行通過

鏈表的表示

由于鏈表的特點（查詢或刪除元素都要從頭結點開始）,所以我們只要在鏈表中定義頭結點即可,另外如果要頻繁用到鏈表的長度，還可以額外定義一個變量來表示。

需要注意的是這個頭結點的定義是有講究的，一般來說頭結點有兩種定義形式，一種是直接以某個元素結點為頭結點,如下

一種是以一個虛擬的節(jié)點作為頭結點，即我們常說的哨兵，如下

定義這個哨兵有啥好處呢，假設我們不定義這個哨兵，來看看鏈表及添加元素的基本操作怎么定義的

/**
* 鏈表中的結點，data代表節(jié)點的值，next是指向下一個節(jié)點的引用
 */
class Node {
int data;// 結點的數(shù)組域，值
    Node next = null;// 節(jié)點的引用，指向下一個節(jié)點
public Node(int data) {
this.data = data;
    }
}

/**
* 鏈表
 */
public class LinkedList {
int length = 0; // 鏈表長度，非必須，可不加
    Node head = null; // 頭結點

public void addNode(int val) {
if (head == null) {
            head = new Node(val);
        } else {
            Node tmp = head;
while (tmp.next != null) {
                tmp = tmp.next;
            }
            tmp.next = new Node(val);
        }
    }
}

發(fā)現(xiàn)問題了嗎，注意看下面代碼

有兩個問題：

每插入一個元素都要對頭結點進行判空比較，如果一個鏈表有很多元素需要插入，就需要進行很多次的判空處理，不是那么高效
頭結點與其他結點插入邏輯不統(tǒng)一（一個需要判空后再插入，一個不需要判空直接插入）,從程序邏輯性來說不是那么合理（因為結點與結點是平級，添加邏輯理應相同）

如果定義了哨兵結點，以上兩個問題都可解決，來看下使用哨兵結點的鏈表定義

public class LinkedList {
int length = 0; // 鏈表長度，非必須，可不加
    Node head = new Node(0); // 哨兵結點
public void addNode(int val) {
        Node tmp = head;
while (tmp.next != null) {
            tmp = tmp.next;
        }
        tmp.next = new Node(val);
    }
}

可以看到，定義了哨兵結點的鏈表邏輯上清楚了很多,不用每次插入元素都對頭結點進行判空，也統(tǒng)一了每一個結點的添加邏輯。

所以之后的習題講解中我們使用的鏈表都是使用定義了哨兵結點的形式。

做了這么多前期的準備工作，終于要開始我們的正餐了：鏈表解題常用套路--翻轉！

鏈表常見解題套路

熱身賽

既然我們要用鏈表解題，那我們首先就構造一個鏈表吧?

題目：給定數(shù)組 1，2，3，4 構造如下鏈表 head-->4---->3---->2---->1

看清楚了，是逆序構造鏈表！順序構造我們都知道怎么構造，對每個元素持續(xù)調用上文代碼定義的 addNode 方法即可（即尾插法），與尾插法對應的，是頭插法，即把每一個元素插到頭節(jié)點后面即可，這樣就能做到逆序構造鏈表，如圖示（以插入1，2 為例）

頭插法比較簡單，直接上代碼,直接按以上動圖的步驟來完成邏輯，如下

public class LinkedList {
int length = 0; // 鏈表長度，非必須，可不加
    Node head = new Node(0); // 哨兵節(jié)點

// 頭插法
public void headInsert(int val) {
// 1.構造新結點
        Node newNode = new Node(val);
// 2.新結點指向頭結點之后的結點
        newNode.next = head.next;
// 3.頭結點指向新結點
        head.next = newNode;
    }

public static void main(String[] args) {
        LinkedList linkedList = new LinkedList();
int[] arr = {1,2,3,4};
// 頭插法構造鏈表
for (int i = 0; i < arr.length; i++) {
            linkedList.headInsert(arr[i]);
        }
// 打印鏈表,將打印 4-->3-->2-->1
        linkedList.printList();
    }
}

小試牛刀

現(xiàn)在我們加大一下難度，來看下曾經(jīng)的 Google 面試題：給定單向鏈表的頭指針和一個節(jié)點指針，定義一個函數(shù)在 O(1) 內刪除這個節(jié)點。

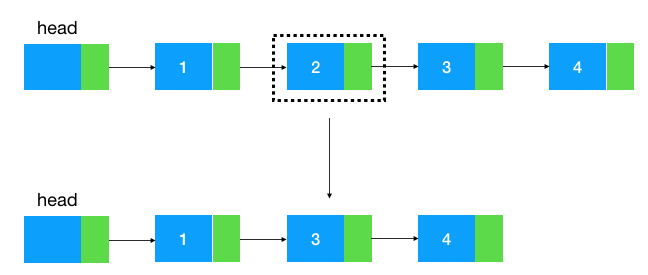如圖示：給定值為 2 的結點，如何把這個結點給刪了。

我們知道，如果給定一個結點要刪除它的后繼結點是很簡單的，只要把這個結點的指針指向后繼結點的后繼結點即可

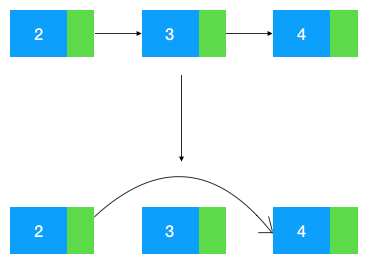
如圖示：給定結點 2，刪除它的后繼結點 3，把結點 2 的 next 指針指向 3 的后繼結點 4 即可。

但給定結點 2，該怎么刪除結點 2 本身呢，注意題目沒有規(guī)定說不能改變結點中的值，所以有一種很巧妙的方法，貍貓換太子！我們先通過結點 2 找到結點 3，再把節(jié)點 3 的值賦給結點 2，此時結點 2 的值變成了 3，這時候問題就轉化成了上圖這種比較簡單的需求，即根據(jù)結點 2 把結點 3 移除即可，看圖

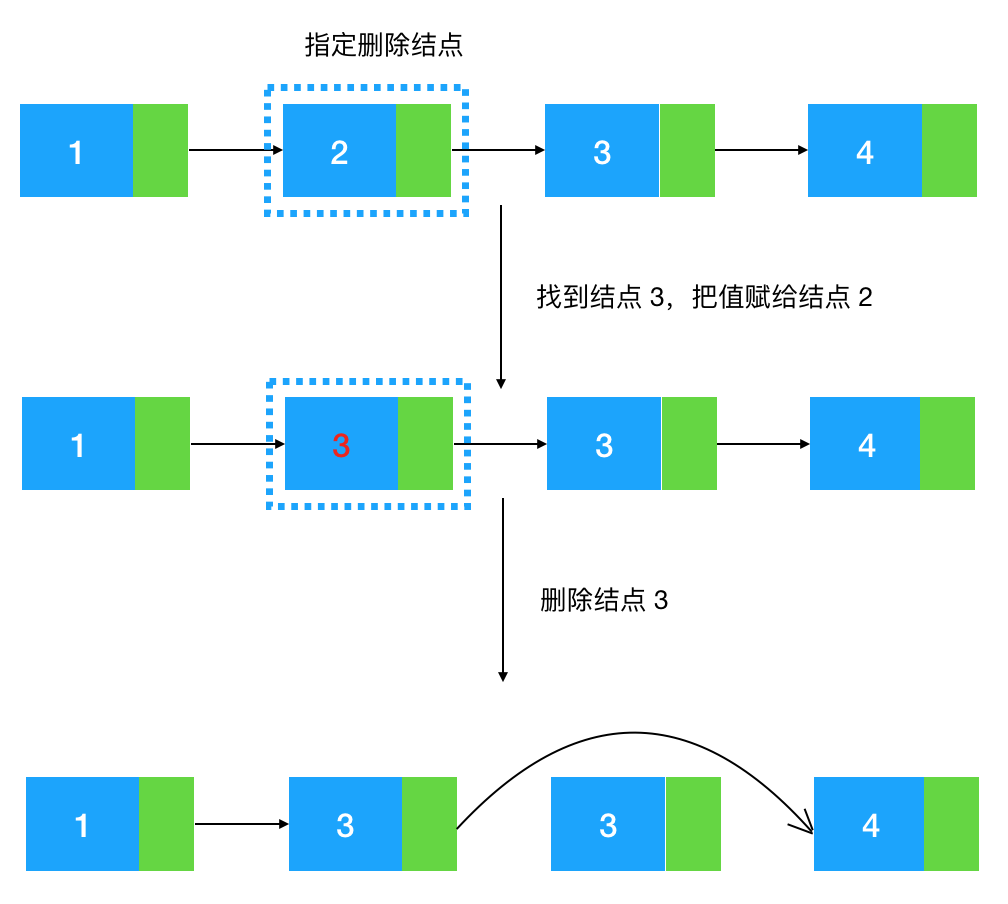
不過需要注意的是這種解題技巧只適用于被刪除的指定結點是中間結點的情況，如果指定結點是尾結點，還是要老老實實地找到尾結點的前繼結點，再把尾結點刪除，代碼如下

/**
 * 刪除指定的結點
 * @param deletedNode
 */
public void removeSelectedNode(Node deletedNode) {
// 如果此結點是尾結點我們還是要從頭遍歷到尾結點的前繼結點，再將尾結點刪除
if (deletedNode.next == null) {
        Node tmp = head;
while (tmp.next != deletedNode) {
            tmp = tmp.next;
        }
// 找到尾結點的前繼結點，把尾結點刪除
        tmp.next = null;
    } else {
        Node nextNode = deletedNode.next;
// 將刪除結點的后繼結點的值賦給被刪除結點
        deletedNode.data = nextNode.data;
// 將 nextNode 結點刪除
        deletedNode.next = nextNode.next;
        nextNode.next = null;
    }
}

入門到進階:鏈表翻轉

接下來我們會重點看一下鏈表的翻轉，鏈表的翻轉可以衍生出很多的變形，是面試中非常熱門的考點，基本上考鏈表必考翻轉！所以掌握鏈表的翻轉是必修課！

什么是鏈表的翻轉:給定鏈表 head-->4--->3-->2-->1，將其翻轉成 head-->1-->2-->3-->4 ，由于翻轉鏈表是如此常見，如此重要，所以我們分別詳細講解下如何用遞歸和非遞歸這兩種方式來解題

遞歸翻轉

關于遞歸的文章之前寫了三篇，如果之前沒讀過的，強烈建議點擊這里查看，總結了遞歸的常見解題套路,給出了遞歸解題的常見四步曲，如果看完對以下遞歸的解題套路會更加深刻，這里不做贅述了，我們直接套遞歸的解題思路：

首先我們要查看翻轉鏈表是否符合遞歸規(guī)律：問題可以分解成具有相同解決思路的子問題，子子問題...，直到最終的子問題再也無法分解。

要翻轉 head--->4--->3-->2-->1 鏈表，不考慮 head 結點，分析 4--->3-->2-->1，仔細觀察我們發(fā)現(xiàn)只要先把 3-->2-->1 翻轉成 3<----2<----1，之后再把 3 指向 4 即可（如下圖示）

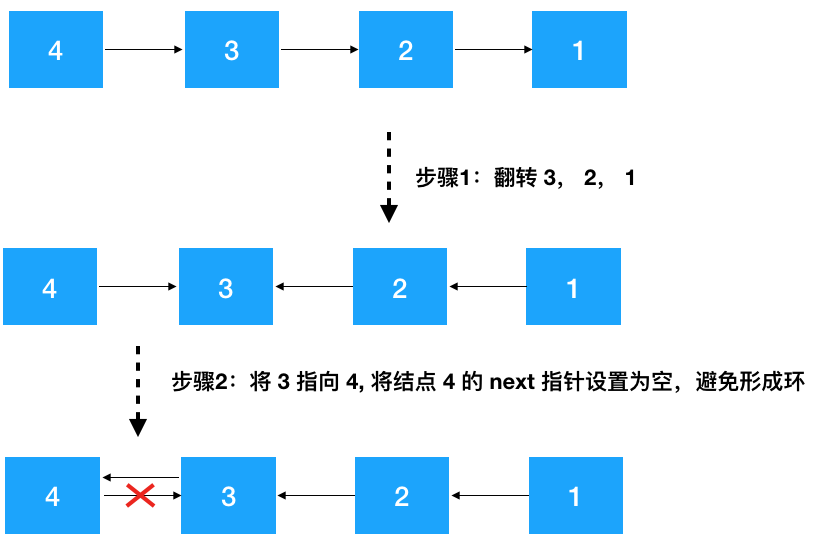
圖：翻轉鏈表主要三步驟

只要按以上步驟定義好這個翻轉函數(shù)的功能即可，這樣由于子問題與最初的問題具有相同的解決思路，拆分后的子問題持續(xù)調用這個翻轉函數(shù)即可達到目的。

注意看上面的步驟1，問題的規(guī)模是不是縮小了（如下圖），從翻轉整個鏈表變成了只翻轉部分鏈表！問題與子問題都是從某個結點開始翻轉，具有相同的解決思路，另外當縮小到只翻轉一個結點時，顯然是終止條件，符合遞歸的條件！之后的翻轉 3-->2-->1, 2-->1 持續(xù)調用這個定義好的遞歸函數(shù)即可！

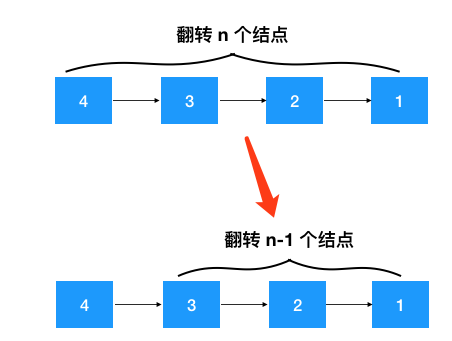
既然符合遞歸的條件，那我們就可以套用遞歸四步曲來解題了（注意翻轉之后 head 的后繼節(jié)點變了，需要重新設置！別忘了這一步）

1、定義遞歸函數(shù),明確函數(shù)的功能根據(jù)以上分析，這個遞歸函數(shù)的功能顯然是翻轉某個節(jié)點開始的鏈表，然后返回新的頭結點

/**
 * 翻轉結點 node 開始的鏈表
 */
public Node invertLinkedList(Node node) {
}

2、尋找遞推公式上文中已經(jīng)詳細畫出了翻轉鏈表的步驟，簡單總結一下遞推步驟如下

針對結點 node (值為 4), 先翻轉 node 之后的結點 ? invert(node->next) ,翻轉之后 4--->3--->2--->1 變成了 4--->3<---2<---1
再把 node 節(jié)點的下個節(jié)點（3）指向 node，node 的后繼節(jié)點設置為空（避免形成環(huán)），此時變成了 4<---3<---2<---1
返回新的頭結點，因為此時新的頭節(jié)點從原來的 4 變成了 1，需要重新設置一下 head

3、將遞推公式代入第一步定義好的函數(shù)中，如下 (invertLinkedList)

/**
 * 遞歸翻轉結點 node 開始的鏈表
 */
public Node invertLinkedList(Node node) {
if (node.next == null) {
return node;
    }

// 步驟 1: 先翻轉 node 之后的鏈表
    Node newHead = invertLinkedList(node.next);

// 步驟 2: 再把原 node 節(jié)點后繼結點的后繼結點指向 node，node 的后繼節(jié)點設置為空(防止形成環(huán))
    node.next.next = node;
    node.next = null;

// 步驟 3: 返回翻轉后的頭結點
return newHead;
}

public static void main(String[] args) {
    LinkedList linkedList = new LinkedList();
int[] arr = {4,3,2,1};
for (int i = 0; i < arr.length; i++) {
        linkedList.addNode(arr[i]);
    }
    Node newHead = linkedList.invertLinkedList(linkedList.head.next);
// 翻轉后別忘了設置頭結點的后繼結點！
    linkedList.head.next = newHead;
    linkedList.printList();      // 打印 1，2，3，4
}

畫外音：翻轉后由于 head 的后繼結點變了，別忘了重新設置哦！

4、計算時間/空間復雜度由于遞歸調用了 n 次 invertLinkedList 函數(shù)，所以時間復雜度顯然是 O(n), 空間復雜度呢，沒有用到額外的空間，但是由于遞歸調用了 ?n 次 invertLinkedList 函數(shù)，壓了 n 次棧，所以空間復雜度也是 O(n)。

遞歸一定要從函數(shù)的功能去理解，從函數(shù)的功能看，定義的遞歸函數(shù)清晰易懂，定義好了之后，由于問題與被拆分的子問題具有相同的解決思路，所以子問題只要持續(xù)調用定義好的功能函數(shù)即可，切勿層層展開子問題，此乃遞歸常見的陷阱！仔細看函數(shù)的功能，其實就是按照下圖實現(xiàn)的。(對照著代碼看，是不是清晰易懂^_^)

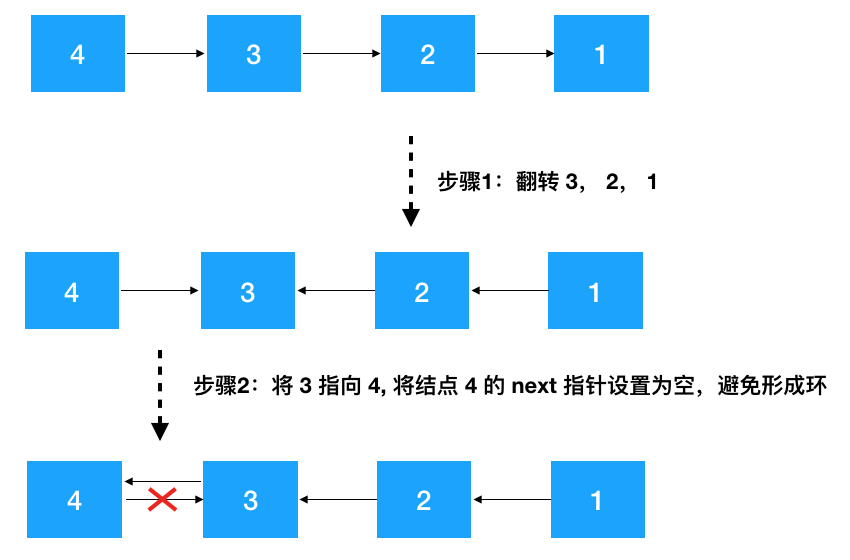
非遞歸翻轉鏈表（迭代解法）

我們知道遞歸比較容易造成棧溢出，所以如果有其他時間/空間復雜度相近或更好的算法，應該優(yōu)先選擇非遞歸的解法,那我們看看如何用迭代來翻轉鏈表，主要思路如下

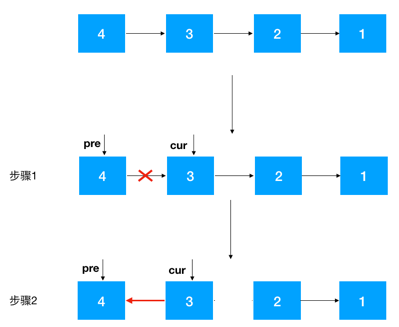
步驟 1：定義兩個節(jié)點：pre, cur ，其中 cur 是 pre 的后繼結點，如果是首次定義，需要把 pre 指向 cur 的指針去掉，否則由于之后鏈表翻轉，cur 會指向 pre，就進行了一個環(huán)(如下)，這一點需要注意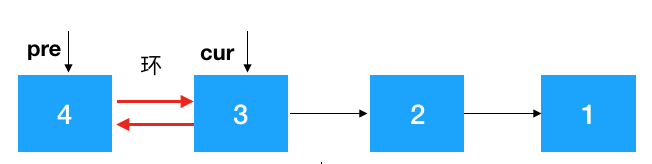

步驟2：知道了 cur 和 pre,翻轉就容易了，把 cur 指向 pre 即可，之后把 cur 設置為 pre ，cur 的后繼結點設置為 cur 一直往前重復此步驟即可,完整動圖如下

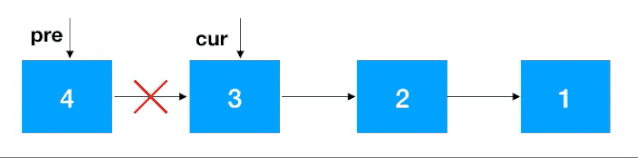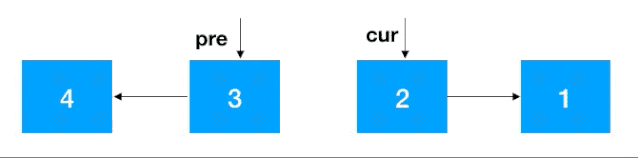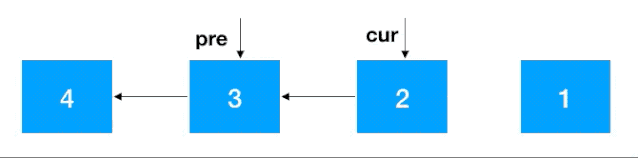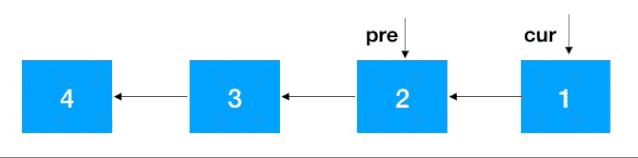
注意：同遞歸翻轉一樣，迭代翻轉完了之后 head 的后繼結點從 4 變成了 1，記得重新設置一下。

知道了解題思路，實現(xiàn)代碼就容易多了，直接上代碼

/**
 * 迭代翻轉
 */
public void iterationInvertLinkedList() {
// 步驟 1
    Node pre = head;
    Node cur = pre.getNext();
    pre.setNext(null);   // pre 是頭結點，避免翻轉鏈表后形成環(huán)

// 步驟 2
while (cur != null) {
/**
         * 務必注意!!!：在 cur 指向 pre 之前一定要先保留 cur 的后繼結點，不然如果 cur 先指向 pre，之后就再也找不到后繼結點了
         */
        Node next = cur.getNext();
        cur.setNext(pre);
        pre = cur;
        cur = next;
    }
// 此時 pre 指向的是原鏈表的尾結點，翻轉后即為鏈表 head 的后繼結點
    head.next = pre;
}

用迭代的思路來做由于循環(huán)了 n 次，顯然時間復雜度為 O(n),另外由于沒有額外的空間使用，也未像遞歸那樣調用遞歸函數(shù)不斷壓棧，所以空間復雜度是 O(1),對比遞歸，顯然應該使用迭代的方式來處理！

花了這么大的精力我們總算把翻轉鏈表給搞懂了，如果大家看了之后幾道翻轉鏈表的變形，會發(fā)現(xiàn)我們花了這么大篇幅講解翻轉鏈表是值得的。

接下來我們來看看鏈表翻轉的變形

變形題 1：給定一個鏈表的頭結點 head,以及兩個整數(shù) from 和 to ,在鏈表上把第 from 個節(jié)點和第 to 個節(jié)點這一部分進行翻轉。例如：給定如下鏈表，from = 2, to = 4 head-->5-->4-->3-->2-->1 將其翻轉后，鏈表變成 head-->5--->2-->3-->4-->1

有了之前翻轉整個鏈表的解題思路，現(xiàn)在要翻轉部分鏈表就相對簡單多了,主要步驟如下:

根據(jù) from 和 to 找到 from-1, from, to, ?to+1 四個結點(注意臨界條件，如果 from 從頭結點開始，則 from-1 結點為空, 翻轉后需要把 to 設置為頭結點的后繼結點， from 和 to 結點也可能超過尾結點,這兩種情況不符合條件不翻轉)。
對 from 到 to 的結點進行翻轉
將 from-1 節(jié)點指向 to 結點，將 from 結點指向 to + 1 結點

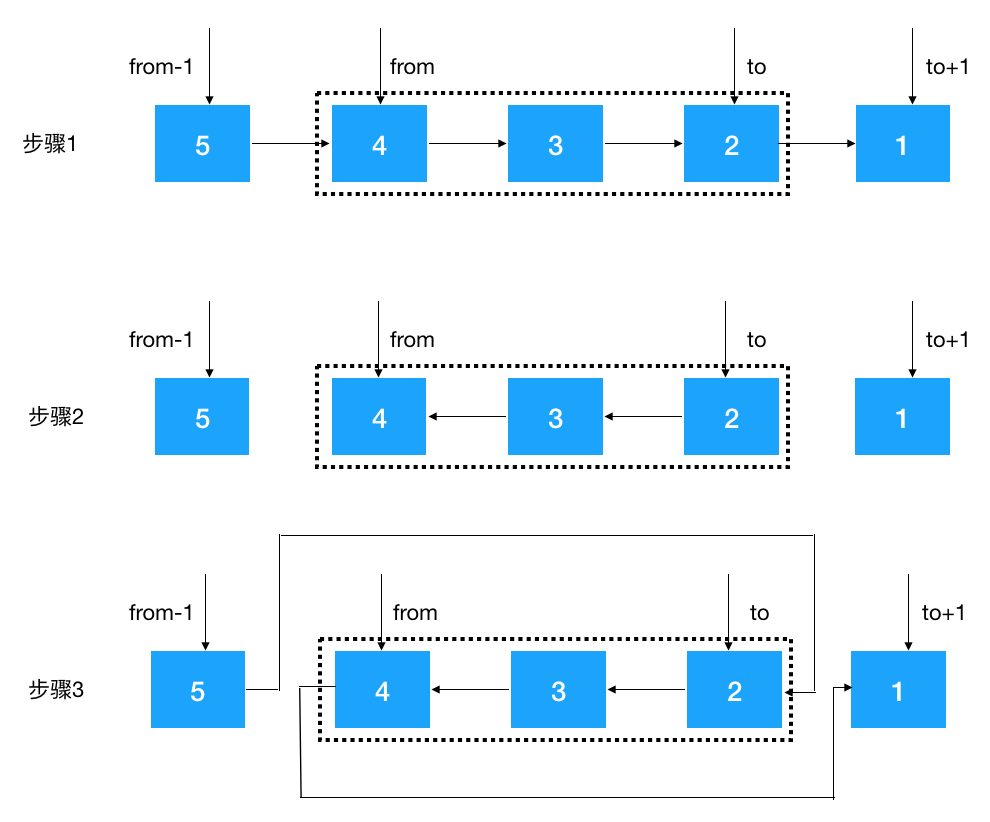
知道了以上的思路，代碼就簡單了,按上面的步驟1，2，3 實現(xiàn)，注釋也寫得很詳細，看以下代碼（對 from 到 to 結點的翻轉我們使用迭代翻轉，當然使用遞歸也是可以的，限于篇幅關系不展開，大家可以嘗試一下）。

/**
 * 迭代翻轉 from 到 to 的結點
 */
public void iterationInvertLinkedList(int fromIndex, int toIndex) throws Exception {

    Node fromPre = null;            // from-1結點
    Node from = null;               // from 結點
    Node to = null;                 // to 結點
    Node toNext = null;             // to+1 結點

// 步驟 1：找到  from-1, from, to,  to+1 這四個結點
    Node tmp = head.next;
int curIndex = 1;      // 頭結點的index為1
while (tmp != null) {
if (curIndex == fromIndex-1) {
            fromPre = tmp;
        } else if (curIndex == fromIndex) {
            from = tmp;
        } else if (curIndex == toIndex) {
            to = tmp;
        } else if (curIndex == toIndex+1) {
            toNext = tmp;
        }
        tmp = tmp.next;
        curIndex++;
    }

if (from == null || to == null) {
// from 或 to 都超過尾結點不翻轉
throw new Exception("不符合條件");
    }

// 步驟2：以下使用循環(huán)迭代法翻轉從 from 到 to 的結點
    Node pre = from;
    Node cur = pre.next;
while (cur != toNext) {
        Node next = cur.next;
        cur.next = pre;
        pre = cur;
        cur = next;
    }

// 步驟3：將 from-1 節(jié)點指向 to 結點（如果從 head 的后繼結點開始翻轉，則需要重新設置 head 的后繼結點），將 from 結點指向 to + 1 結點
if (fromPre != null) {
        fromPre.next = to;
    } else {
        head.next = to;
    }
    from.next = toNext;
}

變形題 2：給出一個鏈表，每 k 個節(jié)點一組進行翻轉，并返回翻轉后的鏈表。k 是一個正整數(shù)，它的值小于或等于鏈表的長度。如果節(jié)點總數(shù)不是 k 的整數(shù)倍，那么將最后剩余節(jié)點保持原有順序。

示例 : 給定這個鏈表：head-->1->2->3->4->5 當 k = 2 時，應當返回: head-->2->1->4->3->5 當 k = 3 時，應當返回: head-->3->2->1->4->5 說明 :

你的算法只能使用常數(shù)的額外空間。
你不能只是單純的改變節(jié)點內部的值，而是需要實際的進行節(jié)點交換。

這道題是 LeetCode 的原題,屬于 hard 級別，如果這一題你懂了，那對鏈表的翻轉應該基本沒問題了，有了之前的翻轉鏈表基礎，相信這題不難。

只要我們能找到翻一組 k 個結點的方法，問題就解決了（之后只要重復對 k 個結點一組的鏈表進行翻轉即可）。

接下來，我們以以下鏈表為例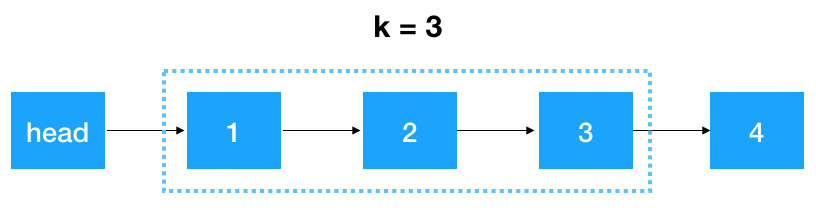來看看怎么翻轉 3 個一組的鏈表（此例中 k = 3）

首先，我們要記錄 3 個一組這一段鏈表的前繼結點,定義為 startKPre,然后再定義一個 step, 從這一段的頭結點 (1）開始遍歷 2 次，找出這段鏈表的起始和終止結點，如下圖示
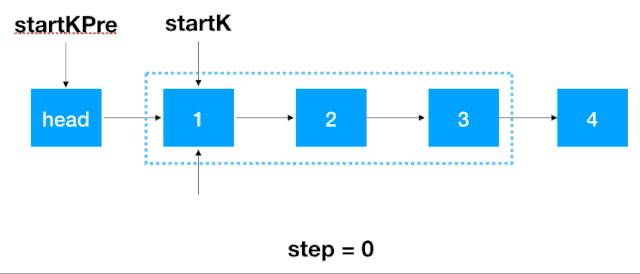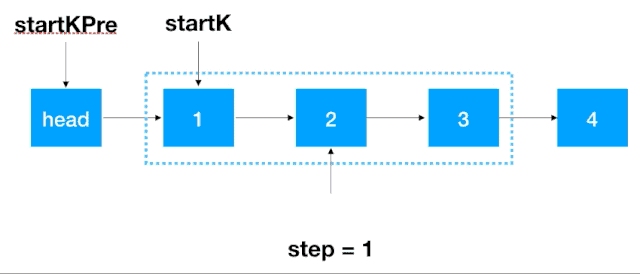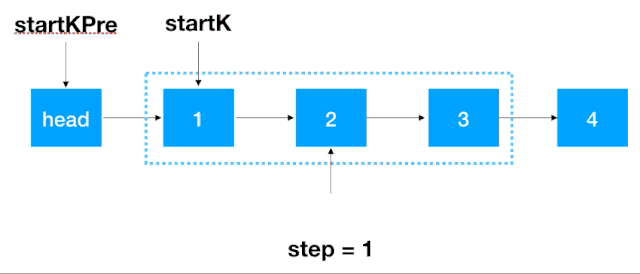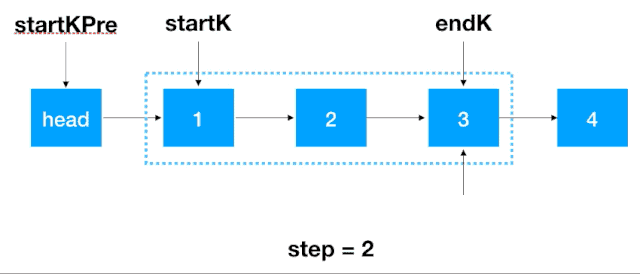
找到 startK 和 endK 之后，根據(jù)之前的迭代翻轉法對 startK 和 endK 的這段鏈表進行翻轉
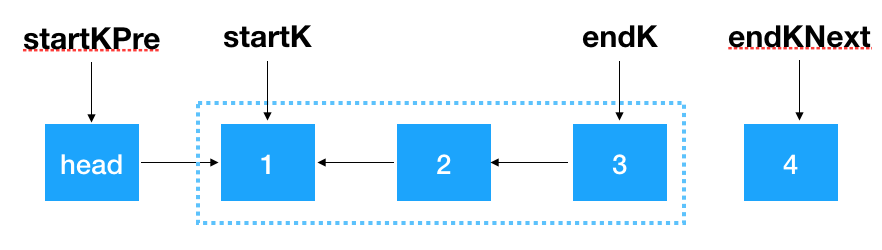
然后將 startKPre 指向 endK,將 startK 指向 endKNext，即完成了對 k 個一組結點的翻轉。

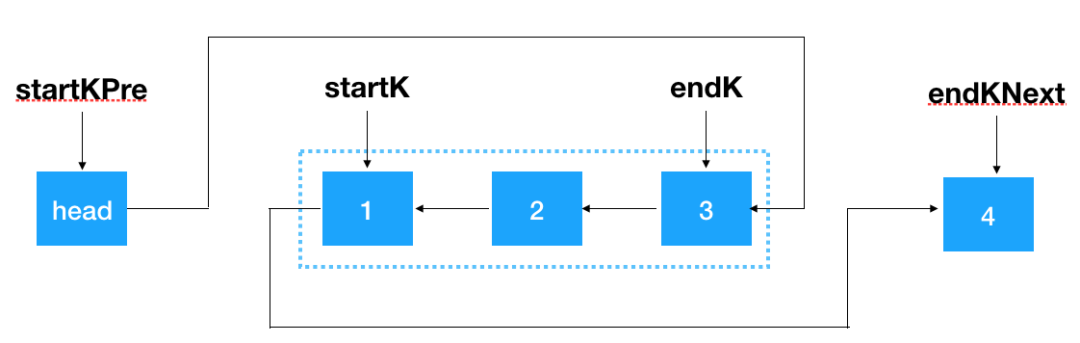
知道了一組 k 個怎么翻轉，之后只要重復對 k 個結點一組的鏈表進行翻轉即可，對照圖示看如下代碼應該還是比較容易理解的

/**
 * 每 k 個一組翻轉鏈表
 * @param k
 */
public void iterationInvertLinkedListEveryK(int k) {
    Node tmp = head.next;
int step = 0;               // 計數(shù)，用來找出首結點和尾結點

    Node startK = null;         // k個一組鏈表中的頭結點
    Node startKPre = head;      // k個一組鏈表頭結點的前置結點
    Node endK;                  // k個一組鏈表中的尾結點
while (tmp != null) {
// tmp 的下一個節(jié)點,因為由于翻轉，tmp 的后繼結點會變,要提前保存
        Node tmpNext = tmp.next;
if (step == 0) {
// k 個一組鏈表區(qū)間的頭結點
            startK = tmp;
            step++;
        } else if (step == k-1) {
// 此時找到了 k 個一組鏈表區(qū)間的尾結點（endK）,對這段鏈表用迭代進行翻轉
            endK = tmp;
            Node pre = startK;
            Node cur = startK.next;
if (cur == null) {
break;
            }
            Node endKNext = endK.next;
while (cur != endKNext) {
                Node next = cur.next;
                cur.next = pre;
                pre = cur;
                cur = next;
            }
// 翻轉后此時 endK 和 startK 分別是是 k 個一組鏈表中的首尾結點
            startKPre.next = endK;
            startK.next = endKNext;

// 當前的 k 個一組翻轉完了，開始下一個 k 個一組的翻轉
            startKPre = startK;
            step = 0;
        } else {
            step++;
        }
        tmp = tmpNext;
    }
}

時間復雜度是多少呢，對鏈表從頭到尾循環(huán)了 n 次，同時每 k 個結點翻轉一次，可以認為總共翻轉了 n 次，所以時間復雜度是O(2n),去掉常數(shù)項，即為 O(n)。注：這題時間復雜度比較誤認為是O(k * n),實際上并不是每一次鏈表的循環(huán)都會翻轉鏈表，只是在循環(huán)鏈表元素每 k 個結點的時候才會翻轉

變形題 3: 變形 2 針對的是順序的 k 個一組翻轉，那如何逆序 k 個一組進行翻轉呢

例如：給定如下鏈表， head-->1-->2-->3-->4-->5 逆序 k 個一組翻轉后，鏈表變成

head-->1--->3-->2-->5-->4?（k = 2 時）?

這道題是字節(jié)跳動的面試題，確實夠變態(tài)的，順序 k 個一組翻轉都已經(jīng)屬于 hard 級別了，逆序 k 個一組翻轉更是屬于 super hard 級別了，不過其實有了之前知識的鋪墊，應該不難，只是稍微變形了一下，只要對鏈表做如下變形即可

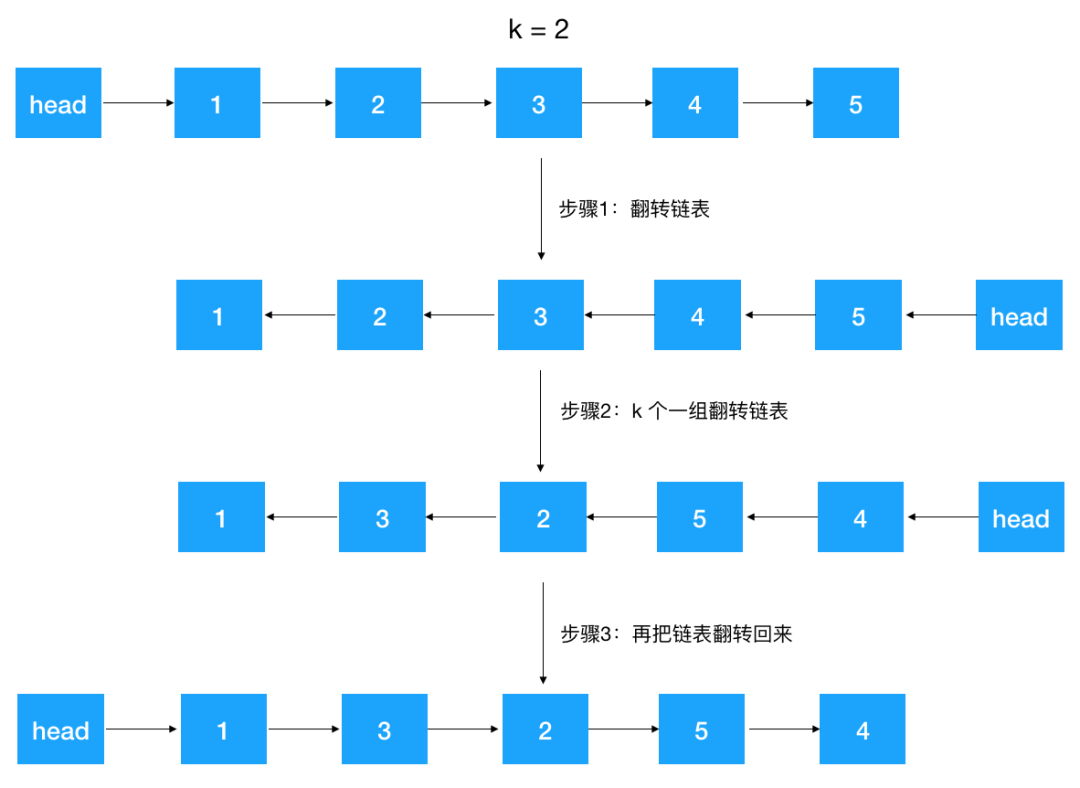
代碼的每一步其實都是用了我們之前實現(xiàn)好的函數(shù)，所以我們之前做的每一步都是有伏筆的哦！就是為了解決字節(jié)跳動這道終極面試題！

/**
 * 逆序每 k 個一組翻轉鏈表
 * @param k
 */
public void reverseIterationInvertLinkedListEveryK(int k) {
// 先翻轉鏈表
    iterationInvertLinkedList();
// k 個一組翻轉鏈表
    iterationInvertLinkedListEveryK(k);
// 再次翻轉鏈表
    iterationInvertLinkedList();
}

由此可見，掌握基本的鏈表翻轉非常重要！難題多是在此基礎了做了相應的變形而已

總結

本文詳細講解了鏈表與數(shù)組的本質區(qū)別，相信大家對兩者的區(qū)別應該有了比較深刻的認識，尤其是程序局部性原理，相信大家看了應該會眼前一亮，之后通過對鏈表的翻轉由淺入深地介紹，相信之后的鏈表翻轉對大家應該不是什么難事了，不過建議大家親自實現(xiàn)一遍文中的代碼哦，這樣印象會更深刻一些！有時候看起來思路是這么一回事，但真正操作起來還是會有不少坑，紙上得來終覺淺，絕知此事要躬行！

文中的所有代碼均已更新在我的 github 地址上: ?https://github.com/allentofight/algorithm,大家如果需要，可以下載運行

其他基礎數(shù)據(jù)結構

1、三分鐘基礎：什么是 2-3-4 樹
2、三分鐘基礎：什么是 2-3 樹？
3、三分鐘基礎：什么是隊列？
4、三分鐘基礎知識：什么是棧？
5、三分鐘基礎：什么是二叉堆？

超詳細:從認識鏈表到學會反轉鏈表