淺談先驗分布和后驗分布

   

    

     

      

       

        
本文約1300字，建議閱讀7分鐘
        
本文通過二項式分布的例子來形象的表達如何選擇先驗分布和計算后驗分布，并闡述了先驗分布和后驗分布是如何轉(zhuǎn)換的，最后對本文進行總結(jié)。
       
      
     
    
   

【例】用一個二值隨機變量x表示拋硬幣的結(jié)果，1表示正面，0表示反面。假設(shè)該硬幣的正反兩面的概率不相同，且正面概率為參數(shù)u，若拋擲N次，正面向上的次數(shù)為m，反面向上的此時為l。求（1）參數(shù)u的后驗概率分布，（2）若連續(xù)拋擲硬幣，求先驗分布和后驗分布參數(shù)的關(guān)系，（3）正面向上的概率

解：（1）多次拋硬幣符合二項式分布，正面向上次數(shù)為m的概率為：

為了滿足共軛先驗的條件，參數(shù)u的先驗分布也應(yīng)與似然函數(shù)的分布相同。即選擇參數(shù)u的先驗分布為beta分布，如下：

等式右邊的系數(shù)部分是為了滿足先驗分布的標準化，即：

參數(shù)u的先驗分布的期望：

后驗分布等于前驗分布和似然函數(shù)的乘積，并對該結(jié)果進行標準化，得到該參數(shù)的后驗分布。

后驗分布形式：

標準化后的結(jié)果：

（2）連續(xù)拋擲硬幣時，當前的參數(shù)分布為先驗分布，與新采樣數(shù)據(jù)的似然函數(shù)進行乘積，再對該結(jié)果進行標準化。容易知道，后驗分布的形式保持不變，指數(shù)發(fā)生變化。

比較數(shù)據(jù)集似然函數(shù)的二項式分布和beta分布，可知a表示正面向上的次數(shù)，b表示反面向上的次數(shù)，由（1）的后驗概率分布可知，當新數(shù)據(jù)的拋擲結(jié)果為m次正面向上，l次反面向上，那么后驗概率分布的指數(shù)表示m+a次正面向上，l+b次反面向上，以此遞推。

若a=1，b=1，參數(shù)u的先驗分布為：

當觀測新數(shù)據(jù)為1次正面向上(m=1)，2次反面向上(l=2)，則后驗分布的指數(shù)表示2次正面向上，3次反面向上。

后驗分布如下圖：

（3）根據(jù)貝葉斯的求和準則與求積準則，參數(shù)u的分布采用后驗分布，得：

參考先驗分布的參數(shù)u的期望，可得后驗分布：

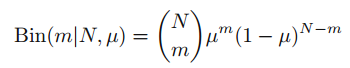
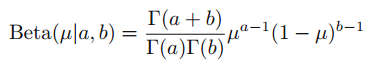
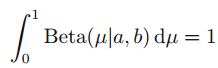
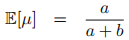
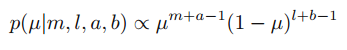
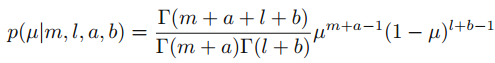
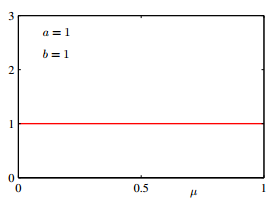
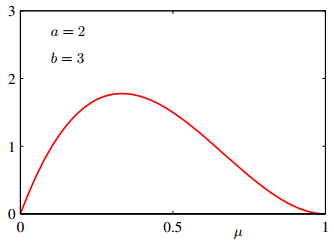
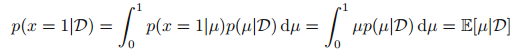
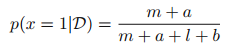
參考：

Christopher M.Bishop <<Pattern Reconition and Machine Learning>>