你以為用了BigDecimal后,計算結(jié)果就一定精確了?


BigDecimal,相信對于很多人來說都不陌生,很多人都知道他的用法,這是一種java.math包中提供的一種可以用來進行精確運算的類型。
很多人都知道,在進行金額表示、金額計算等場景,不能使用double、float等類型,而是要使用對精度支持的更好的BigDecimal。
所以,很多支付、電商、金融等業(yè)務(wù)中,BigDecimal的使用非常頻繁。但是,如果誤以為只要使用BigDecimal表示數(shù)字,結(jié)果就一定精確,那就大錯特錯了!
在之前的一篇文章中,我們介紹過,使用BigDecimal的equals方法并不能驗證兩個數(shù)是否真的相等(為什么阿里巴巴禁止使用BigDecimal的equals方法做等值比較?)。
除了這個情況,BigDecimal的使用的第一步就是創(chuàng)建一個BigDecimal對象,如果這一步都有問題,那么后面怎么算都是錯的!
那到底應(yīng)該如何正確的創(chuàng)建一個BigDecimal?
關(guān)于這個問題,我Review過很多代碼,也面試過很多一線開發(fā),很多人都掉進坑里過。這是一個很容易被忽略,但是又影響重大的問題。
關(guān)于這個問題,在《阿里巴巴Java開發(fā)手冊》中有一條建議,或者說是要求:

?
這是一條【強制】建議,那么,這背后的原理是什么呢?
想要搞清楚這個問題,主要需要弄清楚以下幾個問題:
1、為什么說double不精確?
2、BigDecimal是如何保證精確的?
在知道這兩個問題的答案之后,我們也就大概知道為什么不能使用BigDecimal(double)來創(chuàng)建一個BigDecimal了。
首先,計算機是只認識二進制的,即0和1,這個大家一定都知道。
那么,所有數(shù)字,包括整數(shù)和小數(shù),想要在計算機中存儲和展示,都需要轉(zhuǎn)成二進制。
十進制整數(shù)轉(zhuǎn)成二進制很簡單,通常采用"除2取余,逆序排列"即可,如10的二進制為1010。
但是,小數(shù)的二進制如何表示呢?
十進制小數(shù)轉(zhuǎn)成二進制,一般采用"乘2取整,順序排列"方法,如0.625轉(zhuǎn)成二進制的表示為0.101。
但是,并不是所有小數(shù)都能轉(zhuǎn)成二進制,如0.1就不能直接用二進制表示,他的二進制是0.000110011001100… 這是一個無限循環(huán)小數(shù)。
所以,計算機是沒辦法用二進制精確的表示0.1的。也就是說,在計算機中,很多小數(shù)沒辦法精確的使用二進制表示出來。
那么,這個問題總要解決吧。那么,人們想出了一種采用一定的精度,使用近似值表示一個小數(shù)的辦法。這就是IEEE 754(IEEE二進制浮點數(shù)算術(shù)標(biāo)準)規(guī)范的主要思想。
IEEE 754規(guī)定了多種表示浮點數(shù)值的方式,其中最常用的就是32位單精度浮點數(shù)和64位雙精度浮點數(shù)。
在Java中,使用float和double分別用來表示單精度浮點數(shù)和雙精度浮點數(shù)。
所謂精度不同,可以簡單的理解為保留有效位數(shù)不同。采用保留有效位數(shù)的方式近似的表示小數(shù)。
所以,大家也就知道為什么double表示的小數(shù)不精確了。
接下來,再回到BigDecimal的介紹,我們接下來看看是如何表示一個數(shù)的,他如何保證精確呢?
如果大家看過BigDecimal的源碼,其實可以發(fā)現(xiàn),實際上一個BigDecimal是通過一個"無標(biāo)度值"和一個"標(biāo)度"來表示一個數(shù)的。
在BigDecimal中,標(biāo)度是通過scale字段來表示的。
而無標(biāo)度值的表示比較復(fù)雜。當(dāng)unscaled value超過閾值(默認為Long.MAX_VALUE)時采用intVal字段存儲unscaled value,intCompact字段存儲Long.MIN_VALUE,否則對unscaled value進行壓縮存儲到long型的intCompact字段用于后續(xù)計算,intVal為空。
涉及到的字段就是這幾個:
?public?class?BigDecimal?extends?Number?implements?Comparable<BigDecimal>?{
????????private?final?BigInteger?intVal;
????????private?final?int?scale;?
????????private?final?transient?long?intCompact;
????}
關(guān)于無標(biāo)度值的壓縮機制大家了解即可,不是本文的重點,大家只需要知道BigDecimal主要是通過一個無標(biāo)度值和標(biāo)度來表示的就行了。
除了scale這個字段,在BigDecimal中還提供了scale()方法,用來返回這個BigDecimal的標(biāo)度。
?/**
?????*?Returns?the?scale?of?this?{@code?BigDecimal}.??If?zero
?????*?or?positive,?the?scale?is?the?number?of?digits?to?the?right?of
?????*?the?decimal?point.??If?negative,?the?unscaled?value?of?the
?????*?number?is?multiplied?by?ten?to?the?power?of?the?negation?of?the
?????*?scale.??For?example,?a?scale?of?{@code?-3}?means?the?unscaled
?????*?value?is?multiplied?by?1000.
?????*
?????*?@return?the?scale?of?this?{@code?BigDecimal}.
?????*/
????public?int?scale()?{
????????return?scale;
????}
那么,scale到底表示的是什么,其實上面的注釋已經(jīng)說的很清楚了:
如果scale為零或正值,則該值表示這個數(shù)字小數(shù)點右側(cè)的位數(shù)。如果scale為負數(shù),則該數(shù)字的真實值需要乘以10的該負數(shù)的絕對值的冪。例如,scale為-3,則這個數(shù)需要乘1000,即在末尾有3個0。
如123.123,那么如果使用BigDecimal表示,那么他的無標(biāo)度值為123123,他的標(biāo)度為3。
而二進制無法表示的0.1,使用BigDecimal就可以表示了,及通過無標(biāo)度值1和標(biāo)度1來表示。
我們都知道,想要創(chuàng)建一個對象,需要使用該類的構(gòu)造方法,在BigDecimal中一共有以下4個構(gòu)造方法:
????BigDecimal(int)
????BigDecimal(double)?
????BigDecimal(long)?
????BigDecimal(String)
以上四個方法,創(chuàng)建出來的的BigDecimal的標(biāo)度(scale)是不同的。
其中 BigDecimal(int)和BigDecimal(long) 比較簡單,因為都是整數(shù),所以他們的標(biāo)度都是0。
而BigDecimal(double) 和BigDecimal(String)的標(biāo)度就有很多學(xué)問了。
BigDecimal中提供了一個通過double創(chuàng)建BigDecimal的方法——BigDecimal(double) ,但是,同時也給我們留了一個坑!
因為我們知道,double表示的小數(shù)是不精確的,如0.1這個數(shù)字,double只能表示他的近似值。
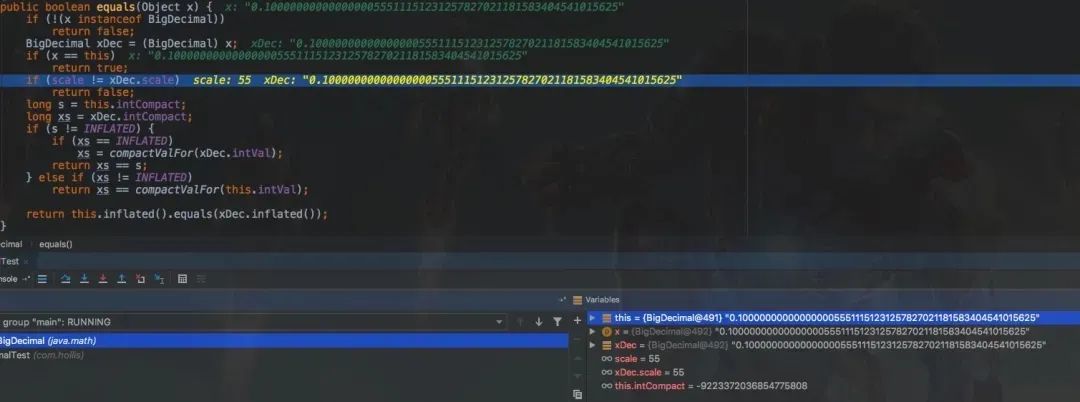
所以,當(dāng)我們使用new BigDecimal(0.1)創(chuàng)建一個BigDecimal 的時候,其實創(chuàng)建出來的值并不是正好等于0.1的。
而是0.1000000000000000055511151231257827021181583404541015625。這是因為doule自身表示的只是一個近似值。
?
所以,如果我們在代碼中,使用BigDecimal(double) 來創(chuàng)建一個BigDecimal的話,那么是損失了精度的,這是極其嚴重的。
那么,該如何創(chuàng)建一個精確的BigDecimal來表示小數(shù)呢,答案是使用String創(chuàng)建。
而對于BigDecimal(String) ,當(dāng)我們使用new BigDecimal("0.1")創(chuàng)建一個BigDecimal 的時候,其實創(chuàng)建出來的值正好就是等于0.1的。
那么他的標(biāo)度也就是1。
但是需要注意的是,new BigDecimal("0.10000")和new BigDecimal("0.1")這兩個數(shù)的標(biāo)度分別是5和1,如果使用BigDecimal的equals方法比較,得到的結(jié)果是false,具體原因和解決辦法參考為什么阿里巴巴禁止使用BigDecimal的equals方法做等值比較?
那么,想要創(chuàng)建一個能精確的表示0.1的BigDecimal,請使用以下兩種方式:
????BigDecimal?recommend1?=?new?BigDecimal("0.1");
????BigDecimal?recommend2?=?BigDecimal.valueOf(0.1);
這里,留一個思考題,BigDecimal.valueOf()是調(diào)用Double.toString方法實現(xiàn)的,那么,既然double都是不精確的,BigDecimal.valueOf(0.1)怎么保證精確呢?
因為計算機采用二進制處理數(shù)據(jù),但是很多小數(shù),如0.1的二進制是一個無線循環(huán)小數(shù),而這種數(shù)字在計算機中是無法精確表示的。
所以,人們采用了一種通過近似值的方式在計算機中表示,于是就有了單精度浮點數(shù)和雙精度浮點數(shù)等。
所以,作為單精度浮點數(shù)的float和雙精度浮點數(shù)的double,在表示小數(shù)的時候只是近似值,并不是真實值。
所以,當(dāng)使用BigDecimal(Double)創(chuàng)建一個的時候,得到的BigDecimal是損失了精度的。
而使用一個損失了精度的數(shù)字進行計算,得到的結(jié)果也是不精確的。
想要避免這個問題,可以通過BigDecimal(String)的方式創(chuàng)建BigDecimal,這樣的情況下,0.1就會被精確的表示出來。
其表現(xiàn)形式是一個無標(biāo)度數(shù)值1,和一個標(biāo)度1的組合。
歡迎關(guān)注微信公眾號:互聯(lián)網(wǎng)全棧架構(gòu),收取更多有價值的信息。
