9個提高代碼運行效率的小技巧你知道幾個?
通常,我們必須在程序的簡潔性與它的運行速度之間做出權(quán)衡。今天我們就來聊一聊如何優(yōu)化程序的性能。
1. 減小程序計算量
1.1 示例代碼
1.2 分析代碼
1.3 改進代碼
2. 提取代碼中的公共部分
2.1 示例代碼
2.2 分析代碼
2.3 改進代碼
3. 消除循環(huán)中低效代碼
3.1 示例代碼
3.2 分析代碼
3.3 改進代碼
4. 消除不必要的內(nèi)存引用
4.1 示例代碼
4.2 分析代碼
4.3 改進代碼
5. 減小不必要的調(diào)用
5.1 示例代碼
5.2 分析代碼
5.3 改進代碼
6. 循環(huán)展開
6.1 示例代碼
6.2 分析代碼
6.3 改進代碼
7. 累計變量,多路并行
7.1 示例代碼
7.2 分析代碼
7.3 改進代碼
8. 重新結(jié)合變換
8.1 示例代碼
8.2 分析代碼
8.3 改進代碼
9 條件傳送風格的代碼
9.1 示例代碼
9.2 分析代碼
9.3 改進代碼
10. 總結(jié)
1. 減小程序計算量
1.1 示例代碼
for (i = 0; i < n; i++) {
int ni = n*i;
for (j = 0; j < n; j++)
a[ni + j] = b[j];
}
1.2 分析代碼
??代碼如上所示,外循環(huán)每執(zhí)行一次,我們要進行一次乘法計算。i = 0,ni = 0;i = 1,ni = n;i = 2,ni = 2n。因此,我們可以把乘法換成加法,以n為步長,這樣就減小了外循環(huán)的代碼量。
1.3 改進代碼
int ni = 0;
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++)
a[ni + j] = b[j];
ni += n; //乘法改加法
}
計算機中乘法指令要比加法指令慢得多。
2. 提取代碼中的公共部分
2.1 示例代碼
??想象一下,我們有一個圖像,我們把圖像表示為二維數(shù)組,數(shù)組元素代表像素點。我們想要得到給定像素的東、南、西、北四個鄰居的總和。并求他們的平均值或他們的和。代碼如下所示。
up = val[(i-1)*n + j ];
down = val[(i+1)*n + j ];
left = val[i*n + j-1];
right = val[i*n + j+1];
sum = up + down + left + right;
2.2 分析代碼
??將以上代碼編譯后得到匯編代碼如下所示,注意下3,4,5行,有三個乘以n的乘法運算。我們把上面的up和down展開后會發(fā)現(xiàn)四格表達式中都有i*n + j。因此,可以提取出公共部分,再通過加減運算分別得出up、down等的值。
leaq 1(%rsi), %rax # i+1
leaq -1(%rsi), %r8 # i-1
imulq %rcx, %rsi # i*n
imulq %rcx, %rax # (i+1)*n
imulq %rcx, %r8 # (i-1)*n
addq %rdx, %rsi # i*n+j
addq %rdx, %rax # (i+1)*n+j
addq %rdx, %r8 # (i-1)*n+j
2.3 改進代碼
long inj = i*n + j;
up = val[inj - n];
down = val[inj + n];
left = val[inj - 1];
right = val[inj + 1];
sum = up + down + left + right;
??改進后的代碼的匯編如下所示。編譯后只有一個乘法。減少了6個時鐘周期(一個乘法周期大約為3個時鐘周期)。
imulq %rcx, %rsi # i*n
addq %rdx, %rsi # i*n+j
movq %rsi, %rax # i*n+j
subq %rcx, %rax # i*n+j-n
leaq (%rsi,%rcx), %rcx # i*n+j+n
...
??對于GCC編譯器來說,編譯器可以根據(jù)不同的優(yōu)化等級,有不同的優(yōu)化方式,會自動完成以上的優(yōu)化操作。下面我們介紹下,那些必須是我們要手動優(yōu)化的。
3. 消除循環(huán)中低效代碼
3.1 示例代碼
??程序看起來沒什么問題,一個很平常的大小寫轉(zhuǎn)換的代碼,但是為什么隨著字符串輸入長度的變長,代碼的執(zhí)行時間會呈指數(shù)式增長呢?
void lower1(char *s)
{
size_t i;
for (i = 0; i < strlen(s); i++)
if (s[i] >= 'A' && s[i] <= 'Z')
s[i] -= ('A' - 'a');
}
3.2 分析代碼
??那么我們就測試下代碼,輸入一系列字符串。
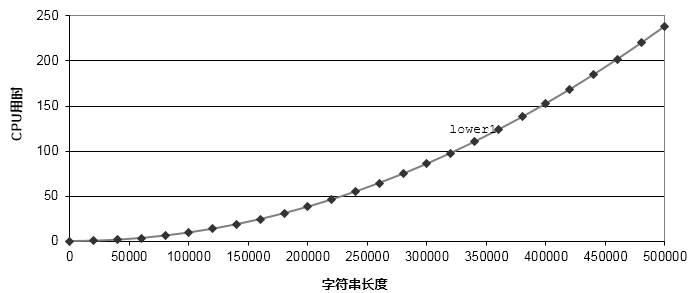
??當輸入字符串長度低于100000時,程序運行時間差別不大。但是,隨著字符串長度的增加,程序的運行時間呈指數(shù)時增長。
??我們把代碼轉(zhuǎn)換成goto形式看下。
void lower1(char *s)
{
size_t i = 0;
if (i >= strlen(s))
goto done;
loop:
if (s[i] >= 'A' && s[i] <= 'Z')
s[i] -= ('A' - 'a');
i++;
if (i < strlen(s))
goto loop;
done:
}
??以上代碼分為初始化(第3行),測試(第4行),更新(第9,10行)三部分。初始化只會執(zhí)行一次。但是測試和更新每次都會執(zhí)行。每進行一次循環(huán),都會對strlen調(diào)用一次。
??下面我們看下strlen函數(shù)的源碼是如何計算字符串長度的。
size_t strlen(const char *s)
{
size_t length = 0;
while (*s != '\0') {
s++;
length++;
}
return length;
}
??strlen函數(shù)計算字符串長度的原理為:遍歷字符串,直到遇到‘\0’才會停止。因此,strlen函數(shù)的時間復(fù)雜度為O(N)。lower1中,對于長度為N的字符串來說,strlen 的調(diào)用次數(shù)為N,N-1,N-2 ... 1。對于一個線性時間的函數(shù)調(diào)用N次,其時間復(fù)雜度接近于O(N2)。
3.3 改進代碼
??對于循環(huán)中出現(xiàn)的這種冗余調(diào)用,我們可以將其移動到循環(huán)外。將計算結(jié)果用于循環(huán)中。改進后的代碼如下所示。
void lower2(char *s)
{
size_t i;
size_t len = strlen(s);
for (i = 0; i < len; i++)
if (s[i] >= 'A' && s[i] <= 'Z')
s[i] -= ('A' - 'a');
}
??將兩個函數(shù)對比下,如下圖所示。lower2函數(shù)的執(zhí)行時間得到明顯提升。
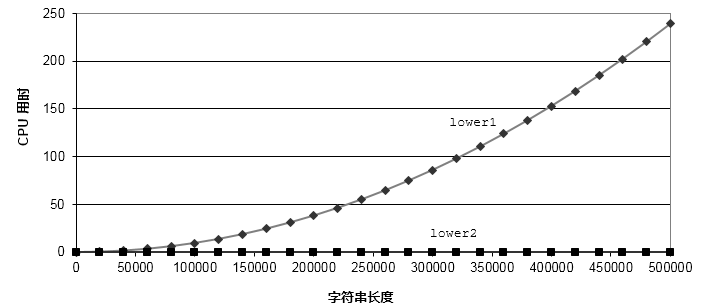
4. 消除不必要的內(nèi)存引用
4.1 示例代碼
??以下代碼作用為,計算a數(shù)組中每一行所有元素的和存在b[i]中。
void sum_rows1(double *a, double *b, long n) {
long i, j;
for (i = 0; i < n; i++) {
b[i] = 0;
for (j = 0; j < n; j++)
b[i] += a[i*n + j];
}
}
4.2 分析代碼
??匯編代碼如下所示。
# sum_rows1 inner loop
.L4:
movsd (%rsi,%rax,8), %xmm0 # 從內(nèi)存中讀取某個值放到%xmm0
addsd (%rdi), %xmm0 # %xmm0 加上某個值
movsd %xmm0, (%rsi,%rax,8) # %xmm0 的值寫回內(nèi)存,其實就是b[i]
addq $8, %rdi
cmpq %rcx, %rdi
jne .L4
??這意味著每次循環(huán)都需要從內(nèi)存中讀取b[i],然后再把b[i]寫回內(nèi)存 。b[i] += b[i] + a[i*n + j]; 其實每次循環(huán)開始的時候,b[i]就是上一次的值。為什么每次都要從內(nèi)存中讀取出來再寫回呢?
4.3 改進代碼
/* Sum rows is of n X n matrix a
and store in vector b */
void sum_rows2(double *a, double *b, long n) {
long i, j;
for (i = 0; i < n; i++) {
double val = 0;
for (j = 0; j < n; j++)
val += a[i*n + j];
b[i] = val;
}
}
??匯編如下所示。
# sum_rows2 inner loop
.L10:
addsd (%rdi), %xmm0 # FP load + add
addq $8, %rdi
cmpq %rax, %rdi
jne .L10
??改進后的代碼引入了臨時變量來保存中間結(jié)果,只有在最后的值計算出來時,才將結(jié)果存放到數(shù)組或全局變量中。
5. 減小不必要的調(diào)用
5.1 示例代碼
??為了方便舉例,我們定義一個包含數(shù)組和數(shù)組長度的結(jié)構(gòu)體,主要是為了防止數(shù)組訪問越界,data_t可以是int,long等類型。具體如下所示。
typedef struct{
size_t len;
data_t *data;
} vec;

??get_vec_element函數(shù)的作用是遍歷data數(shù)組中元素并存儲在val中。
int get_vec_element (*vec v, size_t idx, data_t *val)
{
if (idx >= v->len)
return 0;
*val = v->data[idx];
return 1;
}
??我們將以以下代碼為例開始一步步優(yōu)化程序。
void combine1(vec_ptr v, data_t *dest)
{
long int i;
*dest = NULL;
for (i = 0; i < vec_length(v); i++) {
data_t val;
get_vec_element(v, i, &val);
*dest = *dest * val;
}
}
5.2 分析代碼
??get_vec_element函數(shù)的作用是獲取下一個元素,在get_vec_element函數(shù)中,每次循環(huán)都要與v->len作比較,防止越界。進行邊界檢查是個好習慣,但是每次都進行就會造成效率降低。
5.3 改進代碼
??我們可以把求向量長度的代碼移到循環(huán)體外,同時抽象數(shù)據(jù)類型增加一個函數(shù)get_vec_start。這個函數(shù)返回數(shù)組的起始地址。這樣在循環(huán)體中就沒有了函數(shù)調(diào)用,而是直接訪問數(shù)組。
data_t *get_vec_start(vec_ptr v)
{
return v->data;
}
void combine2 (vec_ptr v, data_t *dest)
{
long i;
long length = vec_length(v);
data_t *data = get_vec_start(v);
*dest = NULL;
for (i=0;i < length;i++)
{
*dest = *dest * data[i];
}
}
6. 循環(huán)展開
6.1 示例代碼
??我們在combine2的代碼上進行改進。
6.2 分析代碼
??循環(huán)展開是通過增加每次迭代計算的元素的數(shù)量,減少循環(huán)的迭代次數(shù)。
6.3 改進代碼
void combine3(vec_ptr v, data_t *dest)
{
long i;
long length = vec_length(v);
long limit = length-1;
data_t *data = get_vec_start(v);
data_t acc = NULL;
/* 一次循環(huán)處理兩個元素 */
for (i = 0; i < limit; i+=2) {
acc = (acc * data[i]) * data[i+1];
}
/* 完成剩余數(shù)組元素的計算 */
for (; i < length; i++) {
acc = acc * data[i];
}
*dest = acc;
}
??在改進后的代碼中,第一個循環(huán)每次處理數(shù)組的兩個元素。也就是每次迭代,循環(huán)索引i加2,在一次迭代中,對數(shù)組元素i和i+1使用合并運算。一般我們稱這種為2×1循環(huán)展開,這種變換能減小循環(huán)開銷的影響。
注意訪問不要越界,正確設(shè)置limit,n個元素,一般設(shè)置界限n-1
7. 累計變量,多路并行
7.1 示例代碼
??我們在combine3的代碼上進行改進。
7.2 分析代碼
??對于一個可結(jié)合和可交換的合并運算來說,比如說整數(shù)加法或乘法,我們可以通過將一組合并運算分割成兩個或更多的部分,并在最后合并結(jié)果來提高性能。
特別注意:不要輕易對浮點數(shù)進行結(jié)合。浮點數(shù)的編碼格式和其他整型數(shù)等都不一樣。
7.3 改進代碼
void combine4(vec_ptr v, data_t *dest)
{
long i;
long length = vec_length(v);
long limit = length-1;
data_t *data = get_vec_start(v);
data_t acc0 = 0;
data_t acc1 = 0;
/* 循環(huán)展開,并維護兩個累計變量 */
for (i = 0; i < limit; i+=2) {
acc0 = acc0 * data[i];
acc1 = acc1 * data[i+1];
}
/* 完成剩余數(shù)組元素的計算 */
for (; i < length; i++) {
acc0 = acc0 * data[i];
}
*dest = acc0 * acc1;
}
??上述代碼用了兩次循環(huán)展開,以使每次迭代合并更多的元素,也使用了兩路并行,將索引值為偶數(shù)的元素累積在變量acc0中,而索引值為奇數(shù)的元素累積在變量acc1中。因此,我們將其稱為”2×2循環(huán)展開”。運用2×2循環(huán)展開。通過維護多個累積變量,這種方法利用了多個功能單元以及它們的流水線能力
8. 重新結(jié)合變換
8.1 示例代碼
??我們在combine3的代碼上進行改進。
8.2 分析代碼
??到這里其實代碼的性能已經(jīng)基本接近極限了,就算做再多的循環(huán)展開性能提升已經(jīng)不明顯了。我們需要換個思路,注意下combine3代碼中第12行的代碼,我們可以改變下向量元素合并的順序(浮點數(shù)不適用)。重新結(jié)合前combine3代碼的關(guān)鍵路徑如下圖所示。
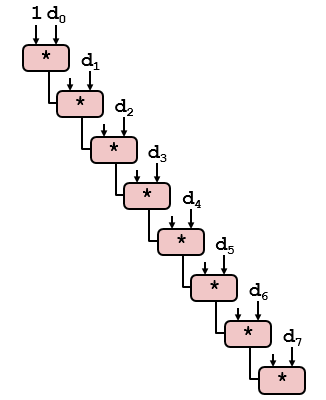
8.3 改進代碼
void combine7(vec_ptr v, data_t *dest)
{
long i;
long length = vec_length(v);
long limit = length-1;
data_t *data = get_vec_start(v);
data_t acc = IDENT;
/* Combine 2 elements at a time */
for (i = 0; i < limit; i+=2) {
acc = acc * (data[i] * data[i+1]);
}
/* Finish any remaining elements */
for (; i < length; i++) {
acc = acc * data[i];
}
*dest = acc;
}
??重新結(jié)合變換能夠減少計算中關(guān)鍵路徑上操作的數(shù)量,這種方法增加了可以并行執(zhí)行的操作數(shù)量了,更好地利用功能單元的流水線能力得到更好的性能。重新結(jié)合后關(guān)鍵路徑如下所示。
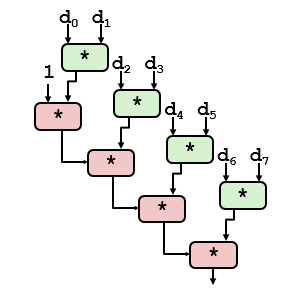
9 條件傳送風格的代碼
9.1 示例代碼
void minmax1(long a[],long b[],long n){
long i;
for(i = 0;i<n;i++){
if(a[i]>b[i]){
long t = a[i];
a[i] = b[i];
b[i] = t;
}
}
}
9.2 分析代碼
??現(xiàn)代處理器的流水線性能使得處理器的工作遠遠超前于當前正在執(zhí)行的指令。處理器中的分支預(yù)測在遇到比較指令時會進行預(yù)測下一步跳轉(zhuǎn)到哪里。如果預(yù)測錯誤,就要重新回到分支跳轉(zhuǎn)的原地。分支預(yù)測錯誤會嚴重影響程序的執(zhí)行效率。因此,我們應(yīng)該編寫讓處理器預(yù)測準確率提高的代碼,即使用條件傳送指令。我們用條件操作來計算值,然后用這些值來更新程序狀態(tài),具體如改進后的代碼所示。
9.3 改進代碼
void minmax2(long a[],long b[],long n){
long i;
for(i = 0;i<n;i++){
long min = a[i] < b[i] ? a[i]:b[i];
long max = a[i] < b[i] ? b[i]:a[i];
a[i] = min;
b[i] = max;
}
}
??在原代碼的第4行中,需要對a[i]和b[i]進行比較,再進行下一步操作,這樣的后果是每次都要進行預(yù)測。改進后的代碼實現(xiàn)這個函數(shù)是計算每個位置i的最大值和最小值,然后將這些值分別賦給a[i]和b[i],而不是進行分支預(yù)測。
10. 總結(jié)
??我們介紹了幾種提高代碼效率的技巧,有些是編譯器可以自動優(yōu)化的,有些是需要我們自己實現(xiàn)的。現(xiàn)總結(jié)如下。
消除連續(xù)的函數(shù)調(diào)用。在可能時,將計算移到循環(huán)外。考慮有選擇地妥協(xié)程序的模塊性以獲得更大的效率。
消除不必要的內(nèi)存引用。引入臨時變量來保存中間結(jié)果。只有在最后的值計算出來時,才將結(jié)果存放到數(shù)組或全局變量中。
展開循環(huán),降低開銷,并且使得進一步的優(yōu)化成為可能。
通過使用例如多個累積變量和重新結(jié)合等技術(shù),找到方法 提高指令級并行。
用功能性的風格重寫條件操作,使得編譯采用條件數(shù)據(jù)傳送。
?------------------------------------------------
雙一流高校研究生團隊創(chuàng)建 ↓
專注于計算機視覺原創(chuàng)并分享相關(guān)知識 ?
聞道有先后,術(shù)業(yè)有專攻,如是而已 ╮(╯_╰)╭
