力扣 (LeetCode)-對稱二叉樹,樹｜刷題打卡

Github來源：力扣 (LeetCode)｜刷題打卡 | 求星星 ? | 給個??關(guān)注，??點贊，??鼓勵一下作者

[已開啟]任務(wù)一：刷題打卡 * 10 篇

哪吒人生信條：如果你所學的東西 處于喜歡 才會有強大的動力支撐。

每天學習編程，讓你離夢想更新一步，感謝不負每一份熱愛編程的程序員，不論知識點多么奇葩，和我一起，讓那一顆四處流蕩的心定下來，一直走下去，加油，2021加油！歡迎關(guān)注加我vx:xiaoda0423，歡迎點贊、收藏和評論

時間：3 月 1 日 ～ 3 月 13 日

• 力扣 (LeetCode)-兩數(shù)之和,有效的括號,兩數(shù)相加｜刷題打卡-3月1日
• 力扣 (LeetCode)-合并兩個有序鏈表,刪除排序數(shù)組中的重復(fù)項,JavaScript筆記｜刷題打卡-3月2日
• 力扣 (LeetCode)-最大子序和,JavaScript數(shù)據(jù)結(jié)構(gòu)與算法（數(shù)組）｜刷題打卡-3月3日
• 針對CSS說一說｜技術(shù)點評-3月4日
• 力扣 (LeetCode)-棧,括號生成 ｜刷題打卡-3月5日
• 原來也沒有那么難！Vue商城開發(fā) | 技術(shù)點評-3月6日
• 力扣 (LeetCode)-加一，隊列 ｜刷題打卡-3月7日
• JavaScript數(shù)據(jù)結(jié)構(gòu)之鏈表 | 技術(shù)點評-3月8日
• JavaScript的數(shù)據(jù)結(jié)構(gòu)-集合 ｜技術(shù)點評-3月9號
• 力扣 (LeetCode)-合并兩個有序數(shù)組,字典,散列表｜刷題打卡-3月10號

前言

如果這篇文章有幫助到你，給個??關(guān)注，??點贊，??鼓勵一下作者，接收好挑戰(zhàn)了嗎？文章公眾號首發(fā)，關(guān)注 程序員哆啦A夢 第一時間獲取最新的文章

??筆芯??~

棧，隊列，鏈表，集合，字典和散列表

樹

樹是一種分層數(shù)據(jù)的抽象模型，最常見的樹的例子是家譜或是公司的組織架構(gòu)圖。

• 一個樹結(jié)構(gòu)包含一些列存在父子關(guān)系的節(jié)點
• 位于樹頂部的節(jié)點叫做根節(jié)點，它沒有父節(jié)點
• 樹中的每個元素都叫作節(jié)點，節(jié)點分內(nèi)部節(jié)點和外部節(jié)點
• 至少有一個子節(jié)點的節(jié)點稱為內(nèi)部節(jié)點
• 沒有子元素的節(jié)點稱為外部節(jié)點或葉節(jié)點
• 子樹由節(jié)點和它的后代構(gòu)成
• 節(jié)點的一個屬性是深度，節(jié)點的深度取決于它的祖先節(jié)點的數(shù)量
• 樹的高度取決于所有節(jié)點深度的最大值

二叉樹和二叉搜索樹

• 二叉樹中的節(jié)點最多只能有兩個子節(jié)點：一個是左側(cè)子節(jié)點，另一個是右側(cè)子節(jié)點
• 二叉搜索樹是二叉樹的一種，但是它只允許你在左側(cè)節(jié)點存儲小的值，在右側(cè)節(jié)點存儲大的值

二叉搜索樹數(shù)據(jù)結(jié)構(gòu)

創(chuàng)建BinarySearchTree類

function BinarySearchTree() {
 var Node = function(key){
 // 聲明一個Node類來表示樹中的每個節(jié)點
  this.key = key;
  this.left = null;
  this.right = null;
 };
 var root = null;
}

• 鏈表：將通過指針來表示節(jié)點之間的關(guān)系
• 雙向鏈表：每個節(jié)點包含兩個指針，一個指向下一個節(jié)點，另一個指向上一個節(jié)點
• 樹，一個指向左側(cè)子節(jié)點，另一個指向右側(cè)子節(jié)點
• insert(key)，向樹中插入一個新的鍵
• search(key)，在樹中查找一個鍵，如果節(jié)點存在，則返回true；如果不存在，則返回false
• inOrderTraverse，通過中序遍歷方式遍歷所有節(jié)點
• preOrderTraverse，通過先序遍歷方式遍歷所有節(jié)點
• postOrderTraverse，通過后序遍歷方式遍歷所有節(jié)點
• min，返回樹中最小的值/鍵
• max，返回樹中最大的值/鍵
• remove(key)，從樹中移除某個鍵

向樹中插入一個鍵

示例：

// 向樹插入一個新鍵的算法
// 要向樹中插入一個新的節(jié)點
this.insert = function(key){ 
 var newNode = new Node(key); //創(chuàng)建用來表示新節(jié)點的Node類實例 
 // 只需要向構(gòu)造函數(shù)傳遞我們想用來插入樹的節(jié)點值，它的左指針和右指針的值會由構(gòu)造函數(shù)自動設(shè)置為null
 if (root === null){ //第二步要驗證這個插入操作是否為一種特殊情況。
 //這個特殊情況就是我們要插入的節(jié)點是樹的第一個節(jié)點 
 root = newNode; 
 } else { 
 insertNode(root,newNode); //將節(jié)點加在非根節(jié)點的其他位置
 } 
};

// 將節(jié)點加在非根節(jié)點的其他位置
var insertNode = function(node, newNode){ 
//  傳入樹的根節(jié)點和要插入的節(jié)點
 if (newNode.key < node.key){ //如果新節(jié)點的鍵小于當前節(jié)點的鍵 
 if (node.left === null){ //需要檢查當前節(jié)點的左側(cè)子節(jié)點
 // 如果它沒有左側(cè)子節(jié)點
 node.left = newNode; //就在那里插入新的節(jié)點
 } else { 
 // 如果有左側(cè)子節(jié)點，需要通過遞歸調(diào)用insertNode方法
 insertNode(node.left, newNode); //繼續(xù)找到樹的下一層
 // 下次將要比較的節(jié)點將會是當前節(jié)點的左側(cè)子節(jié)點
 } 
 } else { 
 if (node.right === null){ 
 //如果節(jié)點的鍵比當前節(jié)點的鍵大，同時當前節(jié)點沒有右側(cè)子節(jié)點
 node.right = newNode; //就在那里插入新的節(jié)點
 } else { 
 insertNode(node.right, newNode); 
 //如果有右側(cè)子節(jié)點，同樣需要遞歸調(diào)用insertNode方法，但是要用來和新節(jié)點比較的節(jié)點將會是右側(cè)子節(jié)點
 } 
 } 
};

示例：

var tree = new BinarySearchTree(); 
tree.insert(11);

樹的遍歷，遍歷一棵樹是指訪問樹的每個節(jié)點并對它們進行某種操作的過程（中序遍歷的一種應(yīng)用就是對樹進行排序操作）

訪問樹的所有節(jié)點有三種方式：中序、先序和后序。

• 中序遍歷是一種以上行順序訪問BST所有節(jié)點的遍歷方式（就是以從最小到最大的順序訪 問所有節(jié)點）

// 中序遍歷的一種應(yīng)用就是對樹進行排序操作
this.inOrderTraverse = function(callback){ 
// 接收一個回調(diào)函數(shù)作為參數(shù)
// 回調(diào)函數(shù)用來定義我們對遍歷到的每個節(jié)點進行的操作
 inOrderTraverseNode(root, callback); //接收一個節(jié)點和對應(yīng)的回調(diào)函數(shù)作為參數(shù)
};

var inOrderTraverseNode = function (node, callback) { 
 if (node !== null) {
 //要通過中序遍歷的方法遍歷一棵樹，首先要檢查以參數(shù)形式傳入的節(jié)點是否為null
 inOrderTraverseNode(node.left, callback); //遞歸調(diào)用相同的函數(shù)來訪問左側(cè)子節(jié)點
 callback(node.key); //接著對這個節(jié)點進行一些操作
 inOrderTraverseNode(node.right, callback); //然后再訪問右側(cè)子節(jié)點
 } 
};

function printNode(value){ //需要創(chuàng)建一個回調(diào)函數(shù) 
 console.log(value); 
} 
tree.inOrderTraverse(printNode); 
//調(diào)用inOrderTraverse方法并將回調(diào)函數(shù)作為參數(shù)傳入

• 先序遍歷是以優(yōu)先于后代節(jié)點的順序訪問每個節(jié)點的。（先序遍歷的一種應(yīng)用是打印一個結(jié)構(gòu)化的文檔）

示例:

this.preOrderTraverse = function(callback){ 
 preOrderTraverseNode(root, callback); 
}; 

preOrderTraverseNode方法的實現(xiàn)如下：

var preOrderTraverseNode = function (node, callback) { 
 if (node !== null) { 
 callback(node.key); //先序遍歷和中序遍歷的不同點是，先序遍歷會先訪問節(jié)點本身 
 preOrderTraverseNode(node.left, callback); 
 //然后再訪問它的左側(cè)子節(jié)點 
 preOrderTraverseNode(node.right, callback); //最后是右側(cè)子節(jié)點 
 } 
};

• 后序遍歷則是先訪問節(jié)點的后代節(jié)點，再訪問節(jié)點本身。（后序遍歷的一種應(yīng)用是計算一個目錄和它的子目錄中所有文件所占空間的大小。）

示例：

this.postOrderTraverse = function(callback){ 
 postOrderTraverseNode(root, callback); 
}; 

postOrderTraverseNode方法的實現(xiàn)如下：

var postOrderTraverseNode = function (node, callback) { 
 if (node !== null) { 
 postOrderTraverseNode(node.left, callback); //后序遍歷會先訪問左側(cè)子節(jié)點 
 postOrderTraverseNode(node.right, callback); //然后是右側(cè)子節(jié)點
 callback(node.key); //最后是父節(jié)點本身 
 } 
};

搜索樹中的值

有三種執(zhí)行的搜索類型：搜索最小值,搜索最大值,搜索特定的值

示例：

// 尋找樹的最小鍵的方法
this.min = function() { 
 return minNode(root); //調(diào)用了minNode方法
 // 傳入樹的根節(jié)點
};

var minNode = function (node) { 
// 允許我們從樹中任意一個節(jié)點開始尋找最小的鍵
 if (node){ 
 while (node && node.left !== null) { //遍歷樹的左邊
 node = node.left; //遍歷樹的左邊 
 } 
 return node.key; 
 } 
 return null; //直到找到樹的最下層
};

// 實現(xiàn)max方法
this.max = function() { 
 return maxNode(root); 
}; 

var maxNode = function (node) { 
 if (node){ 
 while (node && node.right !== null) { //沿著樹的右邊進行遍歷
 node = node.right; // 直到找到最右端的節(jié)點
 } 
 return node.key; 
 } 
 return null; 
};

搜索一個特定的值

// find、search或get方法來查找數(shù)據(jù)結(jié)構(gòu)中的一個特定的值
this.search = function(key){ 
 return searchNode(root, key); 
 //searchNode方法可以用來尋找一棵樹或它的任意子樹中的一個特定的值
}; 

var searchNode = function(node, key){ 
 if (node === null){ 
 //先要驗證作為參數(shù)傳入的node是否合法（不是null）。
 //如果是null的話，說明要找的鍵沒有找到，返回false。 
 return false; 
 } 
 if (key < node.key){ //如果要找的鍵比當前的節(jié)點小
 return searchNode(node.left, key); 
 //那么繼續(xù)在左側(cè)的子樹上搜索 
 
 } else if (key > node.key){ 
 //如果要找的鍵比當前的節(jié)點大，那么就從右側(cè)子節(jié)點開始繼續(xù)搜索
 return searchNode(node.right, key); 
 } else { 
 return true; //否則就說明要找的鍵和當前節(jié)點的鍵相等
 // 就返回true來表示找到了這個鍵
 } 
};

移除一個節(jié)點

示例：

this.remove = function(key){ 
 root = removeNode(root, key); //傳入root和要移除的鍵作為參數(shù)
 // root被賦值為removeNode方法的返回值
};

// removeNode方法的實現(xiàn)

var removeNode = function(node, key){ 

 if (node === null){ 
 //如果正在檢測的節(jié)點是null，那么說明鍵不存在于樹中，所以返回null
 return null; 
 } 
 
 if (key < node.key) { 
 //如果要找的鍵比當前節(jié)點的值小
  node.left = removeNode(node.left, key); 
  //就沿著樹的左邊找到下一個節(jié)點
  return node; //
 } else if (key > node.key){ 
 //如果要找的鍵比當前節(jié)點的值大 
  node.right = removeNode(node.right, key); 
  //那么就沿著樹的右邊找到下一個節(jié)點
  return node; //
 } else { //鍵等于node.key 
  //第一種情況——一個葉節(jié)點 移除一個葉節(jié)點
     if (node.left === null && node.right === null){ 
     //第一種情況是該節(jié)點是一個沒有左側(cè)或右側(cè)子節(jié)點的葉節(jié)點
     // 給這個節(jié)點賦予null值來移除它
     // 還需要處理指針
       node = null; //  需要通過返回null來將對應(yīng)的父節(jié)點指針賦予null值
       return node; //  值已經(jīng)是null了，父節(jié)點指向它的指針也會接收到這個值
       // 要在函數(shù)中返回節(jié)點的值的原因
     } 
 
     //第二種情況——一個只有一個子節(jié)點的節(jié)點
    // 移除有一個左側(cè)或右側(cè)子節(jié)點的節(jié)點
    
     if (node.left === null){ //如果這個節(jié)點沒有左側(cè)子節(jié)點
      node = node.right; //也就是說它有一個右側(cè)子節(jié)點
      // 把對它的引用改為對它右側(cè)子節(jié)點的引用
      return node; //并返回更新后的節(jié)點
     } else if (node.right === null){ 
     //如果這個節(jié)點沒有右側(cè)子節(jié)點 
      node = node.left; //把對它的引用改為對它左側(cè)子節(jié)點的引用 
      return node; //并返回更新后的值 
     } 
 
     //第三種情況——一個有兩個子節(jié)點的節(jié)點
     // 移除有兩個子節(jié)點的節(jié)點
     var aux = findMinNode(node.right); //  

     node.key = aux.key; // 

     node.right = removeNode(node.right, aux.key); // 

     return node; // 
 } 
};

要移除有兩個子節(jié)點的節(jié)點，需要執(zhí)行四個步驟

• 當找到了需要移除的節(jié)點后，需要找到它右邊子樹中最小的節(jié)點
• 然后，用它右側(cè)子樹中最小節(jié)點的鍵去更新這個節(jié)點的值
• 繼續(xù)把右側(cè)子樹中的最小節(jié)點移除，畢竟它已經(jīng)被移至要移除的節(jié)點的位置了
• 向它的父節(jié)點返回更新后節(jié)點的引用

// 找到了要找的鍵（鍵和node.key相等）
var findMinNode = function(node){ 
 while (node && node.left !== null) { 
 node = node.left; 
 } 
 return node; // 在findMinNode中返回了節(jié)點
};

• 二叉搜索樹

自平衡樹

BST存在一個問題：樹的一條分支會有很多層，而其他的分支卻只有幾層的情況。

• Adelson-Velskii-Landi 樹（AVL 樹）
• AVL樹是一種自平衡二叉搜索樹(任何一個節(jié)點左右兩側(cè)子樹的高度之差最多為1)
• AVL樹的不同之處在于我們需要檢驗它的平衡因子，如果有需要，則將其邏輯應(yīng)用于樹的自平衡
• 計算平衡因子
• 需要對每個節(jié)點計算右子樹高度（hr）和左子樹高度（hl）的差值，該值（hr－h(huán)l）應(yīng)為0、1或1
• 如果結(jié)果不是這三個值之一，則需要平衡該AVL樹-這就是平衡因子的概念。

// 計算節(jié)點高度
var heightNode = function(node) { 
 if (node === null) { 
 return -1;
 } else { 
 return Math.max(heightNode(node.left), 
 heightNode(node.right)) + 1; 
 } 
};

// 替換insertNode方法的行 
if ((heightNode(node.left) - heightNode(node.right)) > 1) { 
 // 旋轉(zhuǎn) 
} 

向右子樹插入新節(jié)點時，應(yīng)用同樣的邏輯

// 替換insertNode方法的行 
if ((heightNode(node.right) - heightNode(node.left)) > 1) { 
 // 旋轉(zhuǎn) 
}

• AVL旋轉(zhuǎn):可以執(zhí)行單旋轉(zhuǎn)或雙旋轉(zhuǎn)兩種平衡操作

1. 向左的單旋轉(zhuǎn)
2. 向右的單旋轉(zhuǎn)
3. 向右的雙旋轉(zhuǎn)
4. 向左的雙旋轉(zhuǎn)

示例：

var insertNode = function(node, element) { 

 if (node === null) { 
  node = new Node(element); 
 } else if (element < node.key) { 
  node.left = insertNode(node.left, element); 
     if (node.left !== null) { 
      // 確認是否需要平衡
     } 
 } else if (element > node.key) { 
     node.right = insertNode(node.right, element); 
     if (node.right !== null) { 
      // 確認是否需要平衡
     } 
 } 
 
 return node; 
};

101. 對稱二叉樹

一、題目描述

給定一個二叉樹，檢查它是否是鏡像對稱的。

二、思路分析

• 用遞歸：一棵樹是對稱的 等價于 它的左子樹和右子樹兩棵樹是對稱的，問題就轉(zhuǎn)變?yōu)榕袛鄡煽脴涫欠駥ΨQ。

• 遍歷每一個節(jié)點的時候，如果我都可以通過某種方法知道它對應(yīng)的對稱節(jié)點是誰，這樣的話我直接比較兩者是否一致就行了。

• 第一次遍歷的同時將遍歷結(jié)果存儲到哈希表中，然后第二次遍歷去哈希表取。

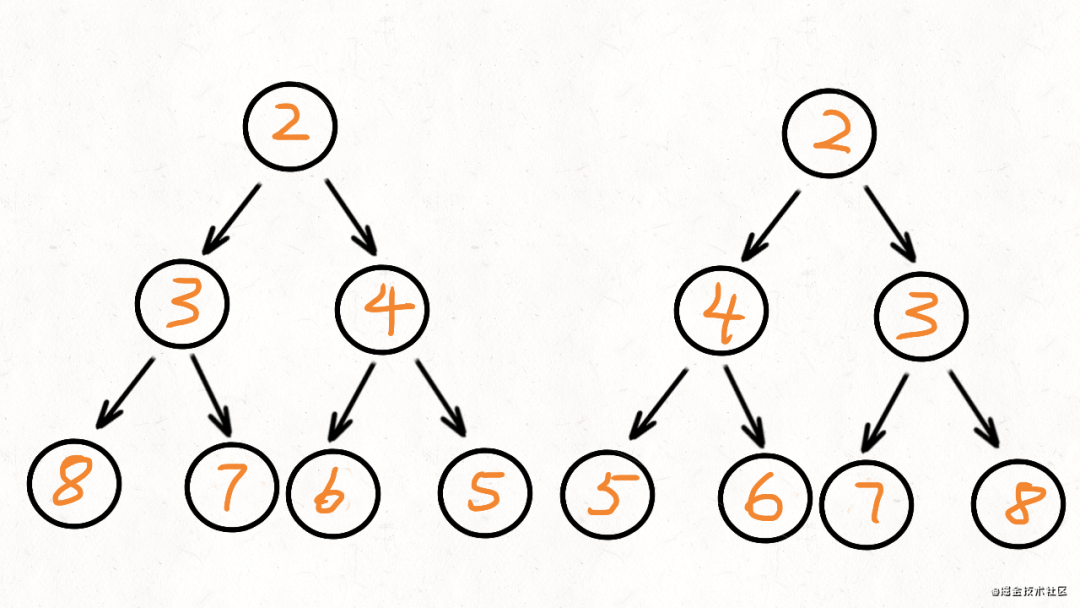
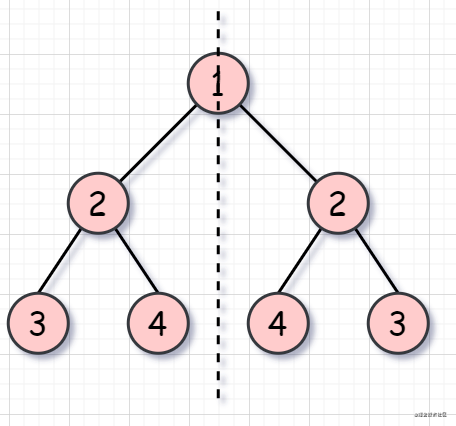
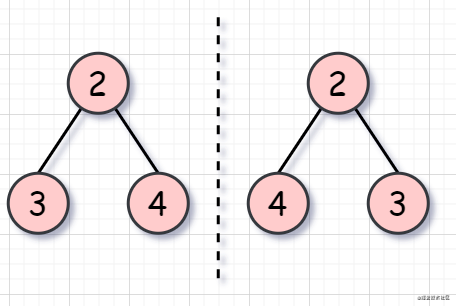
如果同時滿足下面的條件，兩個樹互為鏡像：

• 它們的兩個根結(jié)點具有相同的值
• 每個樹的右子樹都與另一個樹的左子樹鏡像對稱

我們將根節(jié)點的左子樹記做 left，右子樹記做 right。比較 left 是否等于 right，不等的話直接返回就可以了。

如果相當，比較 left 的左節(jié)點和 right 的右節(jié)點，再比較 left 的右節(jié)點和 right 的左節(jié)點。

終止條件：

• left 和 right 不等，或者 left 和 right 都為空
• 遞歸的比較 left，left 和 right.right，遞歸比較 left，right 和 right.left

三、答案代碼

var isSymmetric = function(root) {
    if(!root) return true;
    var stack = [root.left,root.right];
    while(stack.length){
        var p = stack.pop();
        var q = stack.pop();
        if (p === q) continue;
        if (p && q && p.val === q.val) {
            stack.push(p.left, q.right, p.right, q.left);
        } else {
            return false;
        }
    }
    return true;

};

四、總結(jié)

對稱二叉樹,樹

回看筆者往期高贊文章，也許能收獲更多喔！

• 一個合格的初級前端工程師需要掌握的模塊筆記
• Vue.js筆試題解決業(yè)務(wù)中常見問題
• 【初級】個人分享Vue前端開發(fā)教程筆記
• 長篇總結(jié)之JavaScript，鞏固前端基礎(chǔ)
• 前端面試必備ES6全方位總結(jié)
• 達達前端個人web分享92道JavaScript面試題附加回答
• 【圖文并茂，點贊收藏哦！】重學鞏固你的Vuejs知識體系
• 【思維導圖】前端開發(fā)-鞏固你的JavaScript知識體系
• 14期-連肝7個晚上，總結(jié)了計算機網(wǎng)絡(luò)的知識點！（共66條）
• 這是我的第一次JavaScript初級技巧
• localStorage和sessionStorage本地存儲
• HTML5中的拖放功能
• 挑戰(zhàn)前端知識點HTTP/ECMAScript
• 必學必會-音頻和視頻
• 前端170面試題+答案學習整理（良心制作）
• 前端HTML5面試官和應(yīng)試者一問一答
• 哪吒鬧海，席卷圖文學習前端Flex布局
• 騰訊位置服務(wù)開發(fā)應(yīng)用
• 【進階】面試官問我Chrome瀏覽器的渲染原理（6000字長文）
• 面試官一上來就問我Chrome底層原理和HTTP協(xié)議（萬字長文）
• 熬夜總結(jié)了 “HTML5畫布” 的知識點
• this/call/apply/bind（萬字長文）
• HTTP/HTTPS/HTTP2/DNS/TCP/經(jīng)典題
• 執(zhí)行上下文/作用域鏈/閉包/一等公民
• Web頁面制作基礎(chǔ)
• 學習總結(jié)之HTML5劍指前端（建議收藏，圖文并茂）

??關(guān)注+點贊+收藏+評論+轉(zhuǎn)發(fā)??，原創(chuàng)不易，鼓勵筆者創(chuàng)作更好的文章

點贊、收藏和評論

我是Jeskson(達達前端)，感謝各位人才的：點贊、收藏和評論，我們下期見！(如本文內(nèi)容有地方講解有誤，歡迎指出?謝謝，一起學習了)

我們下期見！

文章持續(xù)更新，可以微信搜一搜「 程序員哆啦A夢 」第一時間閱讀，回復(fù)【資料】有我準備的一線大廠資料，本文 http://www.dadaqianduan.cn/#/ 已經(jīng)收錄

github收錄，歡迎Star：https://github.com/webVueBlog/WebFamily