阿基米德為什么沒(méi)能撬開積分學(xué)的大門?
上一篇，我們回顧了歷史上的幾個(gè)計(jì)算事件，見識(shí)了各種計(jì)算表格，但其實(shí)是讓大家一睹幾個(gè)初等函數(shù)那草創(chuàng)未就的時(shí)刻。
即冪函數(shù)、三角函數(shù)、對(duì)數(shù)函數(shù)以及它們的反函數(shù)。這些函數(shù)不僅本身挺有用，還能用來(lái)逼近其他函數(shù)。
最后說(shuō)到開普勒使用對(duì)數(shù)從天文觀測(cè)數(shù)據(jù)中成功發(fā)現(xiàn)了行星運(yùn)動(dòng)第三定律，這不失為一種化曲為直的妙方。
今天，我們?cè)賮?lái)見識(shí)一種以直邊圖形逼近曲邊圖形，以至于求得后者面積的方法。
但是，這么做會(huì)遇到兩個(gè)刺頭，無(wú)窮多項(xiàng)和無(wú)窮小，且看古人怎么破。
1 古人如何求面積
微積分的英文名叫
Calculus
，計(jì)算、演算的意思。而這個(gè)英文單詞來(lái)自拉丁文，是指用作計(jì)算計(jì)數(shù)器的小卵石。
一般認(rèn)為，現(xiàn)代微積分是由 17 世紀(jì)的牛頓和萊布尼茨在前人的大量工作之上獨(dú)立發(fā)展起來(lái)的，包含某種 演算法則 的一門理論。
但就其思想而言，早在古希臘、古代中國(guó)和印度等地已經(jīng)出現(xiàn)，因此我們先來(lái)回顧一下千百年前的相關(guān)工作。
微積分這個(gè)詞義而言，它是一個(gè)縮寫，包括兩部分：
Differential calculus
和
Integral calculus
。其中一部分就是積分演算，從幾何角度看就是求面積，
我們先來(lái)回顧它。
? 窮竭法
我們來(lái)看看古人計(jì)算面積的幾個(gè)典型案例。由于古巴比倫和古埃及過(guò)于遙遠(yuǎn)，此處略過(guò)。
還是從古希臘那會(huì)說(shuō)起吧。
畢達(dá)哥拉斯學(xué)派，信仰萬(wàn)物皆數(shù)。但發(fā)現(xiàn)數(shù)中存在不可公度性問(wèn)題，直接摧毀了他們的信仰。
除了 ，也有說(shuō)法是他們崇尚的圖形五角星（logo）里也被人發(fā)現(xiàn)了不可公度量，隱藏著黃金分割比例以及無(wú)理數(shù) 。
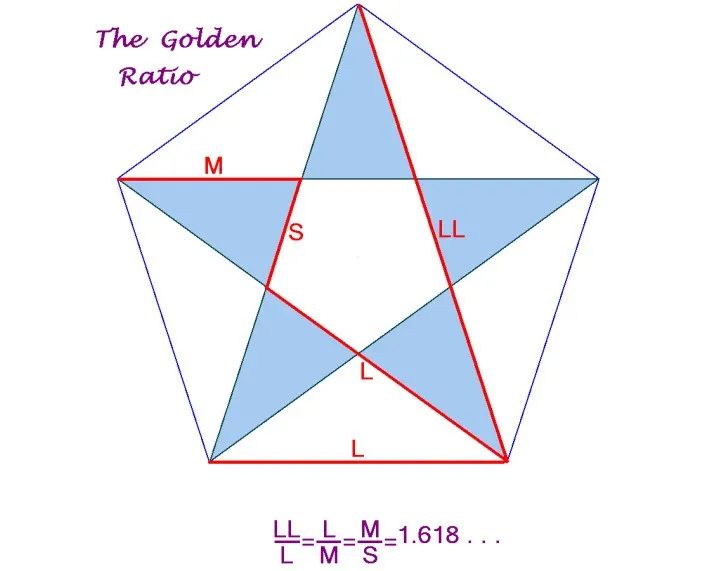
年代久遠(yuǎn)，也只是傳說(shuō)，但如果是真，將直接摧毀他們的信仰。因?yàn)樵谖覀兛磥?lái)這是黃金分割，是美的化身，而在他們眼里這可是魔鬼的利劍，直刺他們的胸口。
之后的古希臘數(shù)學(xué)家似乎患上了焦慮癥，普遍具有對(duì)于無(wú)理數(shù)以及無(wú)窮數(shù)列求和的抗拒心理，因此一度讓畢達(dá)哥拉斯學(xué)派開創(chuàng)的數(shù)學(xué)陷入危機(jī)。
這之間應(yīng)該還受到了著名“杠精”芝諾的影響，他提出了令人十分頭痛的一系列悖論（見附錄）。
為了應(yīng)對(duì)這些挑戰(zhàn)，偉大的歐多克索斯提出了幾何量為基礎(chǔ)的比例論，被歐幾里得收錄于《原本》中。
為了避免無(wú)理數(shù)，比例論不使用數(shù)字來(lái)表示這種比，只拿整數(shù)來(lái)論證比例間的等式關(guān)系，比和比例的觀念是緊密地與幾何連在一起的。
為什么將幾何和算術(shù)加以區(qū)分？可能幾何更具直觀性，如單位正方形的對(duì)角線這樣的無(wú)理長(zhǎng)度，在幾何直觀上很清楚，作圖也是有限的過(guò)程，而根號(hào)
2
?無(wú)論它的表達(dá)形式是序列、小數(shù)還是連分?jǐn)?shù)，都會(huì)表現(xiàn)為一個(gè)無(wú)窮步驟的過(guò)程。
而像論證畢達(dá)哥拉斯這種定理，只需要論證邊長(zhǎng)乘積（面積）之間的關(guān)系，不需要將其量化，數(shù)字似乎可以被邊緣化。
歐多克索斯這么做一定意義上挽救了古希臘數(shù)學(xué)，但也帶來(lái)了后遺癥，例如硬把數(shù)同幾何割裂開了。使得此后兩千多年里幾何學(xué)成為嚴(yán)密數(shù)學(xué)的基礎(chǔ)，而算術(shù)和代數(shù)成為附庸，相關(guān)問(wèn)題往往被轉(zhuǎn)化為幾何問(wèn)題加以研究。
后世幾何學(xué)家如歐幾里得的大作《原本》，以 及阿波羅尼奧斯的大作《 圓錐曲線論》，無(wú)不說(shuō)明歐多克索斯建立的理論框架是成功的。
歐多克索斯的另一個(gè)功勞是建立了數(shù)學(xué)上以明確公理為推理依據(jù)的演繹論證體系，其主要?jiǎng)訖C(jī)是為他的比例論提供邏輯依據(jù)。這點(diǎn)亦被后人歐幾里得所發(fā)揚(yáng)光大。
可見，歐多克索斯的確是古希臘數(shù)學(xué)史上繼往開來(lái)的一位最重要的大數(shù)學(xué)家。
歐多克索斯之后沒(méi)幾十年，亞歷山大大帝開啟希臘化時(shí)代，古希臘的數(shù)學(xué)似乎也跟著發(fā)生了一些微妙的變化。
之前的數(shù)學(xué)家將數(shù)學(xué)思維同實(shí)際需求割裂開來(lái)，他們可以從幾何學(xué)角度考察所有矩形的啥啥性質(zhì)而不去關(guān)心一個(gè)矩形的實(shí)際大小。而希臘化時(shí)代，數(shù)學(xué)向工程化方向演變，更接地氣了。
打造了若無(wú)則萬(wàn)古如長(zhǎng)夜的巨作《原本》的歐幾里得正是處在這個(gè)時(shí)代的前期。
歐幾里得幾何雖然冠絕天下，但等你大功練成準(zhǔn)備大干一場(chǎng)時(shí)，你會(huì)發(fā)現(xiàn)，貌似連圓的面積都不會(huì)計(jì)算啊。
歐幾里得的《原本》里記錄了歐多克索斯使用窮竭法，用圓的內(nèi)接和外接正多邊形證明了圓周率是一個(gè)常數(shù)，但并沒(méi)有去具體計(jì)算。
歐幾里得雖然屬于希臘化時(shí)代，但他的著作還是以匯集前人成果和思想為主。 數(shù)學(xué)上的微妙變化更體現(xiàn)在后面年代以阿基米德為代表的那些數(shù)學(xué)家身上。他們會(huì)更專注于計(jì)算長(zhǎng)度、面積和體積以及在力學(xué)上計(jì)算重心等有用的更加接地氣的問(wèn)題。由于窮竭法在后面會(huì)讓阿基米德如魚得水，此處有必要作個(gè)介紹。
古希臘的安提芬（Antiphon，約前 480 - 前 403）最早表述了窮竭法的樸素思想，他在研究化圓為方問(wèn)題時(shí)，提出了使用圓內(nèi)接正多邊形面積去窮竭圓面積的思想。
歐多克索斯提出一個(gè)命題：任意給定兩個(gè)正的量，在第一個(gè)量中減去比其一半還大的量，不斷重復(fù)這個(gè)過(guò)程，當(dāng)重復(fù)次數(shù)足夠多的時(shí)候，剩下的量必定小于第二個(gè)量。
也就是說(shuō)通過(guò)重復(fù)這種方式可以使得第一個(gè)量變得任意小。這個(gè)定理相當(dāng)于排除了無(wú)窮小量。因?yàn)槿绻鲜雒}中第二個(gè)量取無(wú)窮小量，將與無(wú)窮小量的定義相矛盾。
歐多克索斯將自己的比例理論和安提芬的想法相結(jié)合，正式提出了窮竭法，特別用于論證幾何體的長(zhǎng)度、 面積及體積 相關(guān)的比例問(wèn)題。
正如一個(gè)無(wú)理長(zhǎng)度由它兩邊的有理長(zhǎng)度來(lái)確定一樣，更一般的末知量也可用已知的圖形來(lái)任意地逼近。特別是，用直邊的圖形去逼近曲邊的圖形。
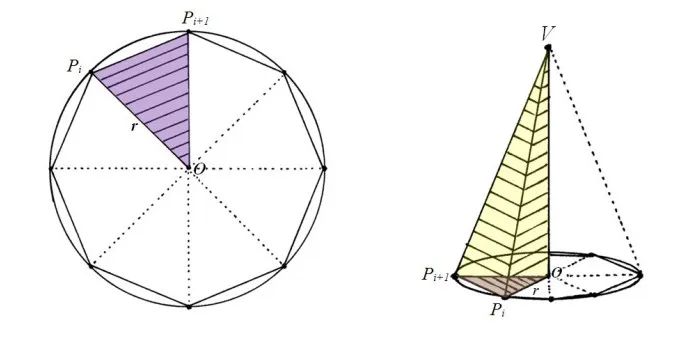
歐多克索斯給出的例子是用內(nèi)接和外切多邊形來(lái)逼近圓，以及用一層層的棱柱來(lái)逼近棱錐。基于比例理論和三角形面積公式，上述兩種情形中的逼近圖形，即多邊形和棱柱的面積和體積都是已知量。
歐多克索斯還使用內(nèi)接和外接多邊形來(lái)逼近圓周，從而證明任一圓的面積跟它的半徑的平方成比例。
窮竭法并不意味著使用無(wú)窮多步驟來(lái)證明面積跟半徑的平方成比例，而是在有限步驟內(nèi)可以否定不成比例性，因此期間往往需要用到歸謬法。窮竭法在論證時(shí)也會(huì)避免涉及無(wú)窮序列。
他那個(gè)時(shí)代貌似對(duì)圓的具體計(jì)算并不感興趣，因?yàn)樗C明了圓周率是常數(shù)，但并沒(méi)有去計(jì)算它的值。
后來(lái)處于希臘化時(shí)代的阿基米德正是繼承這一思想將窮竭法應(yīng)用到實(shí)際計(jì)算中。
? 以直代曲求面積
我們古代相對(duì)比較務(wù)實(shí)，所著的《九章算術(shù)》里就會(huì)涉及計(jì)算圓周的面積，里面提到 徑一而周三，即使用常數(shù) 。
同樣也將圓周率視為常數(shù)，但并沒(méi)有去整虛頭巴腦的證明那套。
之后，東西方分別想辦法計(jì)算圓周率的近似值。
阿基米德（Archimedes，約前 287 - 前 212）進(jìn)一步發(fā)展窮竭法，并用于計(jì)算幾何體的面積和體積問(wèn)題。
阿基米德在靜力學(xué)上的工作是獨(dú)創(chuàng)的，但在數(shù)學(xué)方面的很多工作并沒(méi)有特別新穎之處，他往往受前人啟發(fā)去研究相關(guān)問(wèn)題，進(jìn)而處理了很難的或者前人沒(méi)搞定的問(wèn)題。
阿基米德經(jīng)常談到他是讀了前人著作后得到啟發(fā)想起搞這些問(wèn)題的。例如，歐多克索斯關(guān)于棱錐、圓錐以及圓柱的著作啟發(fā)他去研究球和圓柱，化圓為方的問(wèn)題啟發(fā)他搞拋物線弓形的求積問(wèn)題。
阿基米德在幾何證明中需要的概念，比例論和窮竭法，均是出自前人歐多克索斯之手。但也有他的獨(dú)到之處，例如用多變形來(lái)窮竭拋物線弓形，類似于歐多克索斯對(duì)圓的窮竭，但也有所不同，他是直接求得圖形的面積，不僅僅是為了論證它跟另一個(gè)圖形成比例。
用內(nèi)接正多邊形的周長(zhǎng)來(lái)窮盡圓周長(zhǎng)，從而求得圓周率的近似值；阿基米德最終計(jì)算到正 邊形，并得出 的結(jié)果。
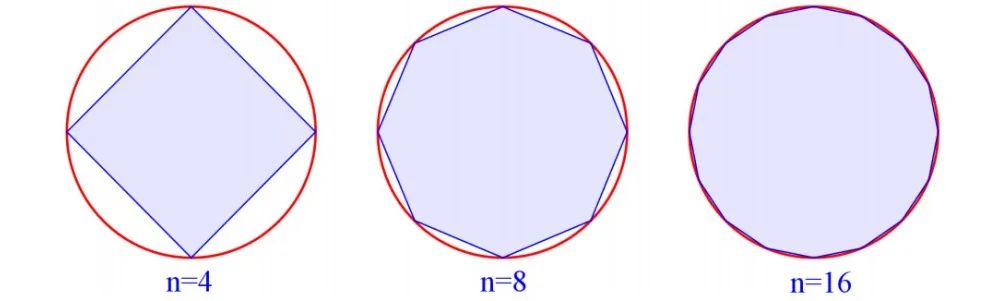看個(gè)動(dòng)圖感受一下不同正多邊形對(duì)圓周率的近似情況，
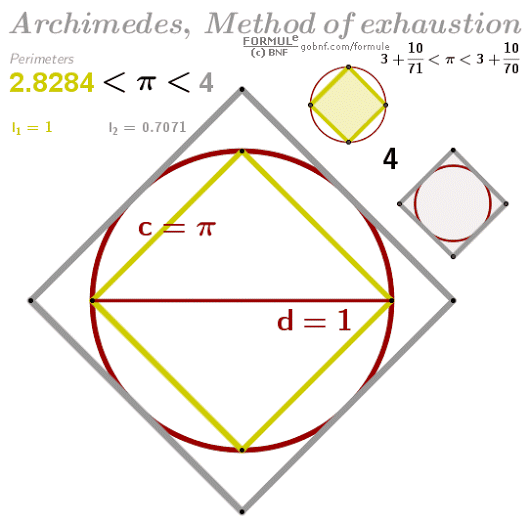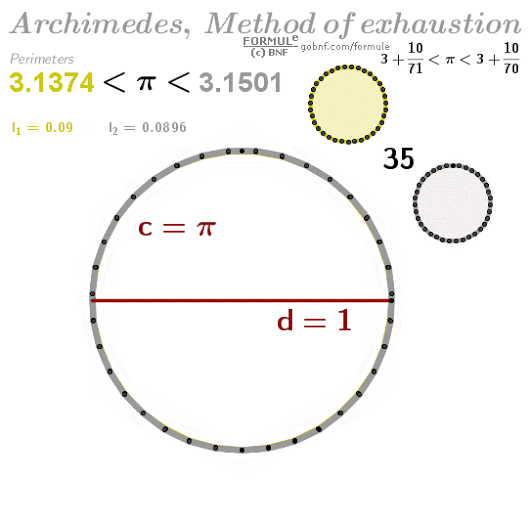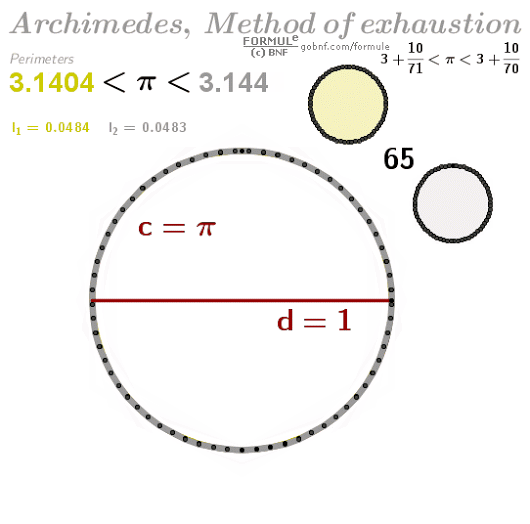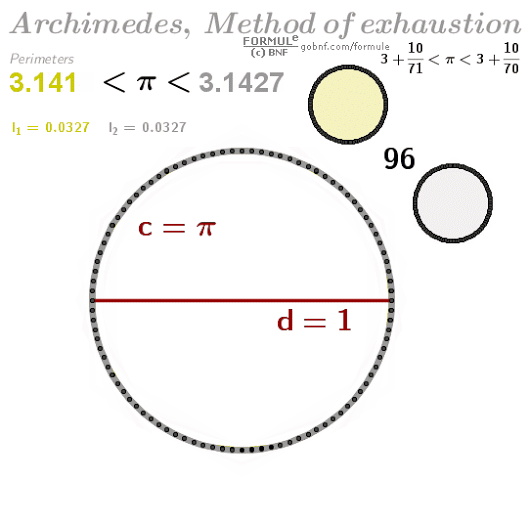
他以內(nèi)接正六邊形開始，逐次加倍邊數(shù)以至逼近圓周率。
劉徽使用正 邊形，先得到圓周率的近似值為 ，后再用圓周率捷法計(jì)算出正 3072 邊形的面積，求得 。
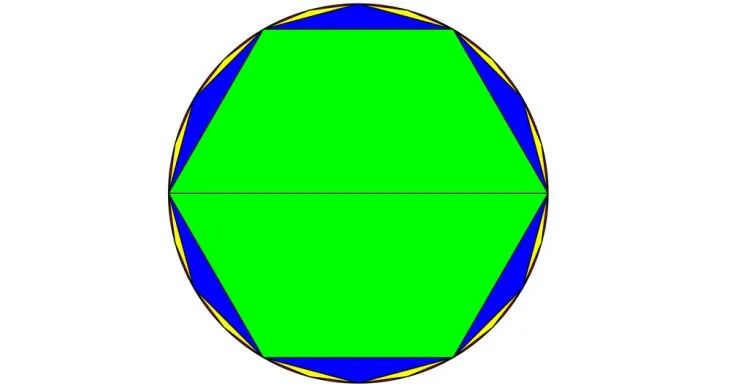
之后的事情大家都知道，南北朝時(shí)期的數(shù)學(xué)家祖沖之進(jìn)一步提升了 精度，此處不展開。
圓的面積大家都想到類似的方法來(lái)逼近了，那如果是其他曲線呢？如何計(jì)算它們圍成的面積呢？
這種問(wèn)題，總體思路還是類似的： 用面積容易求解的直邊圖形（如矩形、三角形等）去填充曲線圍成的區(qū)域 ，用這些直邊圖形面積之和去逼近曲邊圖形的面積。
直觀上看，只要剖得足夠細(xì)致，空隙小到可忽略，總能逼近到讓人滿意。
那這個(gè)方法能不能拿來(lái)計(jì)算其他曲線圍成的面積呢？
接下來(lái)我們來(lái)看看阿基米德如何計(jì)算拋物線與一條直線段圍成的弓形圖形的面積。
阿基米德就這個(gè)問(wèn)題從物理和數(shù)學(xué)兩方面給以了解答。
對(duì)于數(shù)學(xué)方法，阿基米德選擇一系列三角形來(lái)填充拋物線圍起來(lái)的圖形，試圖用已知搏未知。
就是使用面積可求的、相互不重疊的三角形塞滿這個(gè)弓形，這個(gè)弓形的某些邊緣是曲線，因此有限個(gè)三角形無(wú)法填滿它，只能用無(wú)數(shù)個(gè)三角形去窮竭它。
證明的主要思想是將拋物線弓形剖分成無(wú)窮多個(gè)三角形，然后把所有三角形的面積加起來(lái)。
但為了使得構(gòu)造出來(lái)的一系列三角形的面積容易計(jì)算，這些三角形的剖法是有講究的。
例如，下圖中最大的那個(gè)淺藍(lán)色三角形（）的頂點(diǎn) 不是隨意選的，而是該點(diǎn)處的切線與底邊 平行。
阿基米德證明了每個(gè)淺綠色三角形（ 和 ）的面積是藍(lán)色三角形面積的八分之一。
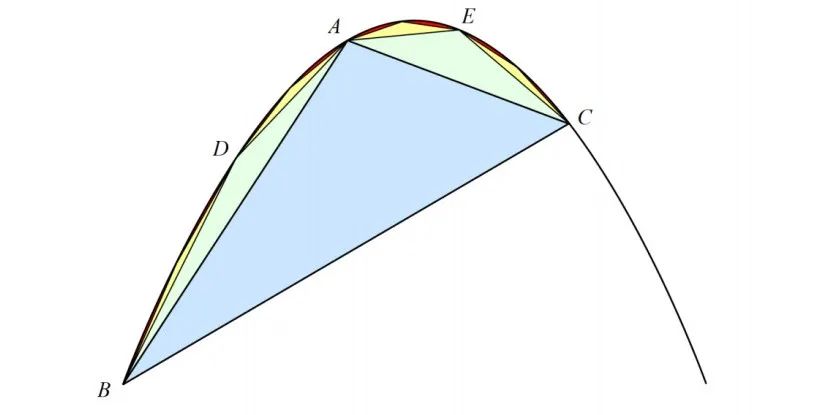
阿基米德通過(guò)計(jì)算發(fā)現(xiàn)：每論新增加的三角形們的面積是上一輪三角形們面積的 。
對(duì)照?qǐng)D來(lái)看，就是 個(gè)淺綠色三角形的面積之和剛好是 個(gè)淺藍(lán)色三角形面積的 ， 個(gè)淺黃色的三角形的面積之和是 個(gè)淺綠色三角形的 ，也就是 個(gè)淺藍(lán)色三角形面積的，一直以這樣的比例增下去。
我們可以看個(gè)特例，選一個(gè)特殊的弓形，如下圖所示，再結(jié)合坐標(biāo)系，用后世的坐標(biāo)幾何（解析幾何）很容易驗(yàn)證上述結(jié)論。
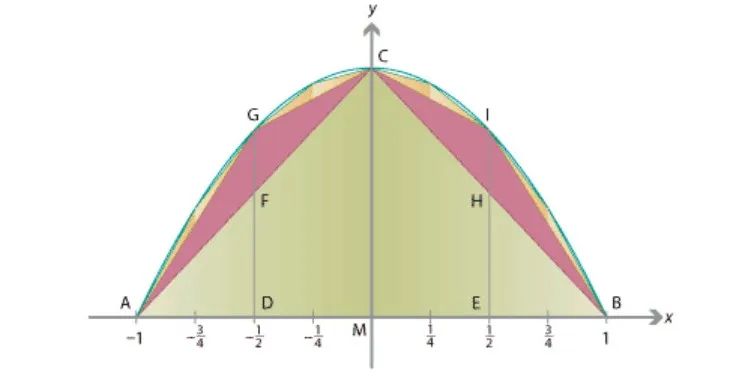
現(xiàn)在可以說(shuō)拋物線弓形可用這樣的多邊形面積來(lái)逼近， 它是在原來(lái)的三角形 上加添一系列三角形而得出的，即所求弓形的面積為
然后，它的值怎么算呢？畢竟有無(wú)窮多項(xiàng)啊。這是一個(gè)幾何級(jí)數(shù)，即等比數(shù)列，用我們現(xiàn)在的知識(shí)自然很容易計(jì)算。
有些資料說(shuō)，阿基米德使用幾何方法求解下式，
上式從幾何上看對(duì)應(yīng)下圖，
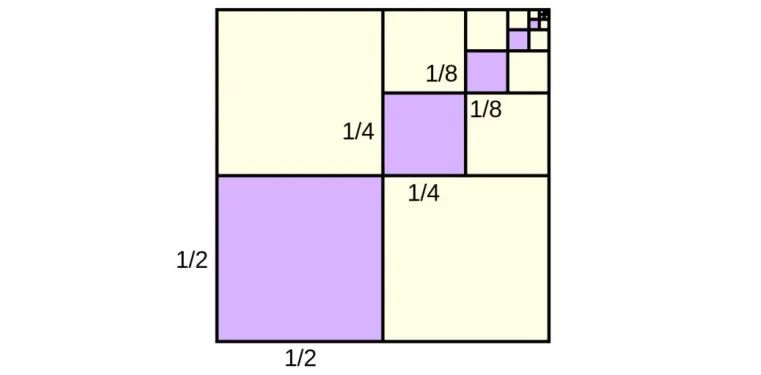
這圖顯示了一個(gè)單位正方形，該正方形已被分解為無(wú)數(shù)個(gè)較小的正方形。每個(gè)連續(xù)的紫色方塊的面積是前一個(gè)方塊的四分之一，拿掉右上角那塊，紫色塊占三分之一，它們的總面積正是我們上面要求的和。
然而，紫色方塊與任何一組黃色方塊全等，因此覆蓋了單位方塊面積的 。因此，弓形面積為三角形 面積的 倍。
這看似合理，也貌似符合古希臘數(shù)學(xué)家慣用幾何方法處理代數(shù)問(wèn)題的思路。
但這實(shí)際上這是后來(lái)人的思想了，雖然可以說(shuō)是等價(jià)，但這樣子并不能反映出古希臘人的邏輯。
古希臘人對(duì)無(wú)窮非常謹(jǐn)慎，一方面反映在不可公度性（無(wú)理數(shù)），另一方面可能深受芝諾悖論（見附錄）的影響。
對(duì)于無(wú)窮，他們是很認(rèn)真的，概念上還提出了潛無(wú)窮和實(shí)無(wú)窮之分。那揮散不盡的無(wú)窮項(xiàng)像幽靈一樣的總是讓嚴(yán)謹(jǐn)?shù)墓畔ＥD人心理抗拒。
那么疑問(wèn)來(lái)了，阿基米德如何應(yīng)對(duì)這個(gè)棘手的問(wèn)題呢？雖然現(xiàn)在已經(jīng)不再使用，但還是有必要了解一下他們所謂的窮竭法的套路，以有窮論證潛在的無(wú)窮。
簡(jiǎn)而言之：阿基米德處理的是這個(gè)級(jí)數(shù)的前面若干項(xiàng)的部分和，并使用雙重歸謬法論證這個(gè)部分和與 可以任意接近。
取有限項(xiàng)來(lái)任意逼近某個(gè)值，就這里的問(wèn)題而言，即弓形面積與 中取有限項(xiàng)之和的差是可以比任何預(yù)先指定的量要小。
然后，阿基米德用歸謬法證明拋物線弓形的面積 不能大于也不能小于 ，其中 是三角形 的面積。
他首先證明該等比數(shù)列的前 項(xiàng)滿足下式，
即前 項(xiàng)再加一項(xiàng) ，把剩余的無(wú)窮多項(xiàng)一次性補(bǔ)足，從而實(shí)現(xiàn)避免處理無(wú)窮項(xiàng)。
我們可以用幾何級(jí)數(shù)前 項(xiàng)之和的公式來(lái)證明。
（1）證明：若面積 大于 ，那他可以取有限個(gè)三角形，使其和與弓形面積之差小于任一給定的量，因此可使有限個(gè)三角形的面積和 大于 ，即
假設(shè) 有 項(xiàng)，則但據(jù)式 有，
因此，
與前面式子矛盾。
（2）假設(shè)拋物線弓形面積 小于 ，則 是一個(gè)確定的數(shù)。由于阿基米德所作的三角形是越來(lái)越小趨近于 的，于是可以得到一系列內(nèi)接三角形，使得它們滿足
其中 是序列中的第 項(xiàng)，它在幾何上代表 個(gè)三角形之和。但由式 有，
于是
從而得出，
與內(nèi)接三角形之和總是小于弓形面積矛盾，因此 不成立。
這一步證明的直觀思路是：只要取得足夠多項(xiàng)，讓 盡可能小， 與 之間的差距也會(huì)盡可能地小，因此 隨著三角形的增多逐漸趨近于 。
當(dāng)然，阿基米德實(shí)際上求出了無(wú)窮幾何級(jí)數(shù)的和，因當(dāng)式 中的 變?yōu)闊o(wú)窮時(shí) 趨于 ，于是無(wú)窮級(jí)數(shù)之和為 。
這證明是不是相當(dāng)漂亮和完美！感覺(jué)內(nèi)含極限思想，并且比較好地規(guī)避了無(wú)窮項(xiàng)求和的心理障礙。
這個(gè)方法如此優(yōu)秀，為什么在后來(lái)的教材中沒(méi)有流行呢？
我們不妨反過(guò)來(lái)思考一下，這種方法有什么不足之處呢？
它能否也可以拿來(lái)計(jì)算圓的面積啊。但你可以試一下，它似乎又不行，能出來(lái) 這樣的有理數(shù)嗎？
阿基米德的三角形窮竭式逼近法在計(jì)算拋物線弓形面積時(shí)取得了輝煌的成功，但它并不適合其它更多曲線，即便在古希臘人那里并沒(méi)有那么多種曲線，但這個(gè)方法并不適用于計(jì)算它們的面積。
阿基米德也想到用矩形來(lái)逼近曲線下的面積，但在處理像拋物線弓形面積時(shí)并沒(méi)有用三角形來(lái)得優(yōu)美，因此并沒(méi)有成為一種通用方案。
這種技法似乎還缺了點(diǎn)火候，像一壇老酒那樣還需要醞釀，只不過(guò)這時(shí)間似乎長(zhǎng)了點(diǎn)，將近兩千年。
總之，阿基米德的這個(gè)方法需要針對(duì)正涉及的圖形設(shè)計(jì)專門的求和方案，因此缺乏通用性。
這是市場(chǎng)最大的痛點(diǎn)，好的理論工具就得有通用性。常見的曲線（圖形）拿來(lái)，可以使用同一個(gè)方法求面積。
除此之外，阿基米德還各個(gè)擊破地搞定了很多面積公式和體積公式，離創(chuàng)立積分學(xué)似乎似乎只有一步之遙，但其實(shí)他也有時(shí)代局限性。
阿基米德的局限：導(dǎo)致他的方法缺乏通用性的原因是多方面的，比如對(duì)無(wú)窮級(jí)數(shù)的規(guī)避，更不用說(shuō)對(duì)其進(jìn)行運(yùn)算，這將在牛頓時(shí)代興起；古希臘那個(gè)時(shí)代的整體局限性，對(duì)無(wú)理數(shù)的抗拒，以至于令代數(shù)方法的獨(dú)立發(fā)展幾乎停滯，更不用說(shuō)坐標(biāo)幾何以及函數(shù)這些概念和方法。
阿基米德使用了 窮竭法 成功計(jì)算了拋物線弓形面積，避免了直面 無(wú)窮級(jí)數(shù) 和 無(wú)窮小 ，似乎非常完美，但似乎又錯(cuò)過(guò)了什么。
阿基米德有句名言：給我一個(gè)支點(diǎn)，我就能撬動(dòng)地球。
那么，給阿基米德什么工具，他就能撬開積分學(xué)呢？
2 附錄
? 1、窮竭法
窮竭法是一種求圖形面積的方法，其通過(guò)構(gòu)造一個(gè)內(nèi)接多邊形序列，使這些多邊形的面積收斂到所求圖形面積。
如果這個(gè)多邊形序列構(gòu)造得當(dāng)，那么其第 項(xiàng)的面積與所求圖形面積之差在 足夠大時(shí)便可以小于任意給定正數(shù)。
因?yàn)檫@個(gè)面積差可以任意小，是故該圖形面積的可能值便系統(tǒng)性的被該多邊形序列中的成員的面積所給出的一系列下界窮竭掉。
窮竭法在應(yīng)用時(shí)一般須配合歸謬法。具體來(lái)說(shuō)，為了求某圖形面積，而將其與第二個(gè)圖形來(lái)作比較。證明過(guò)程牽涉到先假定所求面積大于第二圖形的面積，并證明其偽，接下來(lái)假定所求面積小于第二圖形的面積，并將其也證偽。
? 2、芝諾悖論
二分法悖論：由于運(yùn)動(dòng)的物體在到達(dá)目的地前必須到達(dá)其半路上的點(diǎn)，若假設(shè)空間無(wú)限可分則有限距離包括無(wú)窮多點(diǎn)，于是運(yùn)動(dòng)的物體會(huì)在有限時(shí)間內(nèi)經(jīng)過(guò)無(wú)限多點(diǎn)。因此，運(yùn)動(dòng)不可能開始。
相當(dāng)于產(chǎn)生了如下數(shù)列，
這種描述要求一個(gè)人完成無(wú)限數(shù)量的任務(wù)，芝諾認(rèn)為這是不可能的。
該序列還提出了第二個(gè)問(wèn)題，因?yàn)樗话\(yùn)動(dòng)的第一距離，因?yàn)槿魏?strong style="color:rgb(51,85,119);">可能的第一距離都可以分成兩半，它成不了第一距離。因此，運(yùn)動(dòng)甚至無(wú)法開始。那么自相矛盾的結(jié)論將是，在任何有限距離上的運(yùn)動(dòng)既不能完成也不能開始，因此所有運(yùn)動(dòng)都必須是一種幻覺(jué)。
阿喀琉斯悖論：阿喀琉斯是古希臘神話中善跑的英雄。在他和烏龜?shù)母?jìng)賽中，他速度為烏龜十倍，烏龜在前面 米跑，他在后面追，但他不可能追上烏龜。因?yàn)樵诟?jìng)賽中，追者首先必須到達(dá)被追者的出發(fā)點(diǎn)，當(dāng)阿基里斯追到 米時(shí)，烏龜已經(jīng)又向前爬了 米，于是，一個(gè)新的起點(diǎn)產(chǎn)生了；阿基里斯必須繼續(xù)追，而當(dāng)他追到烏龜爬的這 米時(shí)，烏龜又已經(jīng)向前爬了 米，阿基里斯只能再追向那個(gè) 米。就這樣，烏龜會(huì)制造出無(wú)窮個(gè)起點(diǎn)，它總能在起點(diǎn)與自己之間制造出一個(gè)距離，不管這個(gè)距離有多小，但只要烏龜不停地奮力向前爬，阿基里斯就永遠(yuǎn)也追不上烏龜！
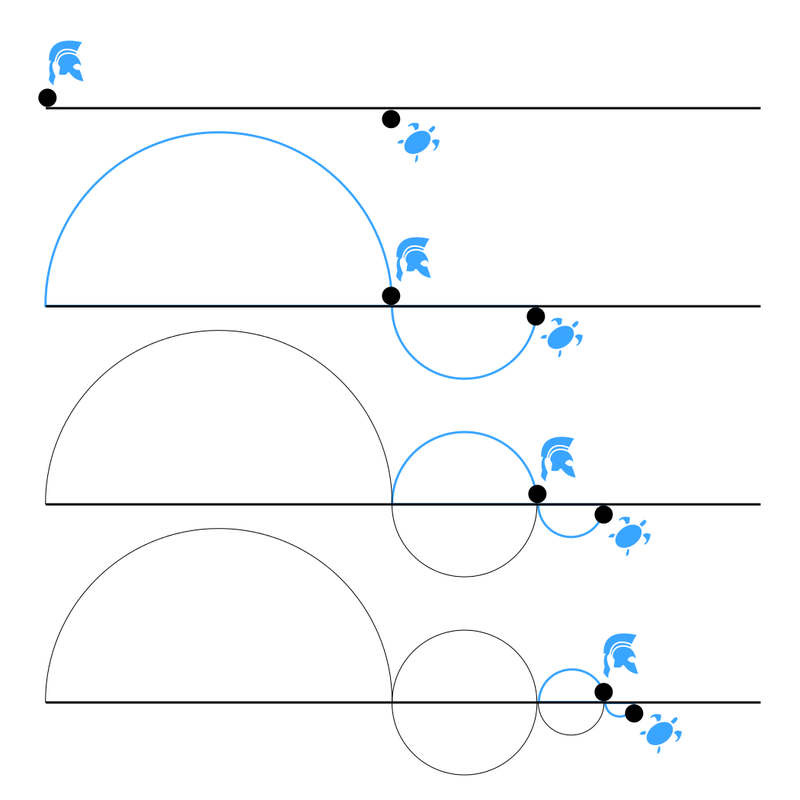
這些悖論是古希臘數(shù)學(xué)家對(duì)無(wú)窮級(jí)數(shù)可以產(chǎn)生有限和的想法產(chǎn)生抗拒心理的原因。
不可能在有限的時(shí)間內(nèi)遍歷無(wú)窮多個(gè)事物。這里的問(wèn)題并不是有限的總量，這可以通過(guò)求極限來(lái)應(yīng)對(duì)，而是完成一項(xiàng)具有無(wú)限步數(shù)的任務(wù)，由無(wú)限的定義可知，達(dá)不到最后一個(gè)步驟，因此該任務(wù)無(wú)法完成。
飛矢不動(dòng): 芝諾認(rèn)為，物體為了發(fā)生運(yùn)動(dòng)，必須改變它所占據(jù)的位置。他舉了一個(gè)飛行中的箭的例子。在任何一個(gè)瞬間，箭頭既不會(huì)移動(dòng)到它所在的位置，也不會(huì)移動(dòng)到它不移動(dòng)的位置。它不能移動(dòng)到它不存在的地方，因?yàn)樗苿?dòng)到那里沒(méi)有時(shí)間流逝；它不能移動(dòng)到它所在的地方，因?yàn)樗呀?jīng)在那里了。換句話說(shuō)，在每一個(gè)瞬間都沒(méi)有運(yùn)動(dòng)發(fā)生。如果一切在每一瞬間都是靜止的，而時(shí)間完全是由瞬間組成的，那么運(yùn)動(dòng)是不可能的。
前兩個(gè)悖論劃分空間，而這個(gè)悖論從劃分時(shí)間開始 — 不是劃分為片段，而是劃分為點(diǎn)。
三個(gè)悖論，一個(gè)說(shuō)沒(méi)有第一步，因此運(yùn)動(dòng)不能開始；一個(gè)說(shuō)沒(méi)有最后結(jié)束那步，因此任務(wù)完不成；一個(gè)說(shuō)每一個(gè)瞬間都是靜止的，運(yùn)動(dòng)在任何時(shí)刻都不能發(fā)生。
芝諾對(duì)數(shù)學(xué)的影響
嚴(yán)格來(lái)說(shuō)，芝諾并不是數(shù)學(xué)家，用現(xiàn)在的話說(shuō)更像個(gè)杠精。但他是否影響了古希臘的數(shù)學(xué)發(fā)展呢？影響肯定是有的，他那些悖論至少讓古希臘人對(duì)實(shí)無(wú)窮產(chǎn)生了敬畏和抗拒，甚至因此而改變了主流研究方向。
柏拉圖的《巴門尼德》討論的主要話題之一是芝諾的觀點(diǎn)，芝諾也是書中的主角之一，因此在柏拉圖學(xué)園中討論芝諾悖論應(yīng)該是常事。
而歐多克索斯有段時(shí)間正是在柏拉圖學(xué)園中攻讀和研究數(shù)學(xué)與哲學(xué)。在稍后的時(shí)間里創(chuàng)立了幾何量的比例論（《原本》第五卷中的主要內(nèi)容），從而克服了因發(fā)現(xiàn)不可公度量而出現(xiàn)的數(shù)學(xué)危機(jī)；并完善了窮竭法，巧妙地處理了無(wú)窮小問(wèn)題。
在希臘數(shù)學(xué)發(fā)展的這個(gè)關(guān)鍵時(shí)刻，很難說(shuō)芝諾沒(méi)有對(duì)它的發(fā)展作出過(guò)有意義的貢獻(xiàn)。
畢達(dá)哥拉斯學(xué)派曾假定存在無(wú)窮小的基本線段（初等線段），想以此來(lái)克服因發(fā)現(xiàn)不可公度量而引起的困難。芝諾所反對(duì)的正是這種處理無(wú)窮小的不準(zhǔn)確的做法，從而迫使畢達(dá)哥拉斯學(xué)派的下一代數(shù)學(xué)家去探求更好、更準(zhǔn)確的基礎(chǔ)。
因此，有數(shù)學(xué)史家說(shuō)：芝諾畢竟以非數(shù)學(xué)的語(yǔ)言，記錄下了最早同連續(xù)性和無(wú)限性格斗的人們所遭遇到的困難。芝諾的功績(jī)?cè)谟诎褎?dòng)和靜的關(guān)系、無(wú)限和有限的關(guān)系、連續(xù)和離散的關(guān)系明顯地?cái)[了出來(lái)，并進(jìn)行了辨證。
休息一下，未完待續(xù)