在本文中，我們試圖更好地理解批量大小對訓(xùn)練神經(jīng)網(wǎng)絡(luò)的影響。具體而言，我們將涵蓋以下內(nèi)容：

1. 什么是Batch Size？
2. 為什么Batch Size很重要？
3. 小批量和大批量如何憑經(jīng)驗(yàn)執(zhí)行？
4. 為什么大批量往往性能更差，如何縮小性能差距？

什么是Batch Size？

訓(xùn)練神經(jīng)網(wǎng)絡(luò)以最小化以下形式的損失函數(shù)：

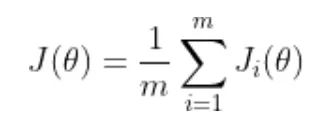
• theta 代表模型參數(shù)
• m 是訓(xùn)練數(shù)據(jù)樣本的數(shù)量
• i 的每個值代表一個單一的訓(xùn)練數(shù)據(jù)樣本
• J_i 表示應(yīng)用于單個訓(xùn)練樣本的損失函數(shù)

通常，這是使用梯度下降來完成的，它計算損失函數(shù)相對于參數(shù)的梯度，并在該方向上邁出一步。隨機(jī)梯度下降計算訓(xùn)練數(shù)據(jù)子集 B_k 上的梯度，而不是整個訓(xùn)練數(shù)據(jù)集。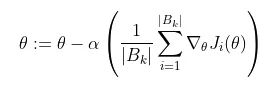

B_k 是從訓(xùn)練數(shù)據(jù)集中采樣的一批，其大小可以從 1 到 m（訓(xùn)練數(shù)據(jù)點(diǎn)的總數(shù)）。這通常稱為批量大小為 |B_k| 的小批量訓(xùn)練。我們可以將這些批次級梯度視為“true”梯度的近似值，即整體損失函數(shù)相對于 theta 的梯度。我們使用小批量是因?yàn)樗鼉A向于更快地收斂，因?yàn)樗恍枰耆闅v訓(xùn)練數(shù)據(jù)來更新權(quán)重。

為什么Batch Size很重要？

Keskar 等人指出，隨機(jī)梯度下降是連續(xù)的，且使用小批量，因此不容易并行化 。使用更大的批量大小可以讓我們在更大程度上并行計算，因?yàn)槲覀兛梢栽诓煌墓ぷ鞴?jié)點(diǎn)之間拆分訓(xùn)練示例。這反過來可以顯著加快模型訓(xùn)練。

然而，較大的批大小雖然能夠達(dá)到與較小的批大小相似的訓(xùn)練誤差，但往往對測試數(shù)據(jù)的泛化效果更差 。訓(xùn)練誤差和測試誤差之間的差距被稱為“泛化差距”。因此，“holy grail”是使用大批量實(shí)現(xiàn)與小批量相同的測試誤差。這將使我們能夠在不犧牲模型準(zhǔn)確性的情況下顯著加快訓(xùn)練速度。

實(shí)驗(yàn)是如何設(shè)置的？

我們將使用不同的批量大小訓(xùn)練神經(jīng)網(wǎng)絡(luò)并比較它們的性能。

數(shù)據(jù)集：我們使用 Cats and Dogs 數(shù)據(jù)集，該數(shù)據(jù)集包含 23,262 張貓和狗的圖像，在兩個類之間的比例約為 50/50。由于圖像大小不同，我們將它們?nèi)空{(diào)整為相同大小。我們使用 20% 的數(shù)據(jù)集作為驗(yàn)證數(shù)據(jù)，其余作為訓(xùn)練數(shù)據(jù)。

評估指標(biāo)：我們使用驗(yàn)證數(shù)據(jù)上的二元交叉熵?fù)p失作為衡量模型性能的主要指標(biāo)。

基礎(chǔ)模型：定義了一個受 VGG16 啟發(fā)的基礎(chǔ)模型，在其中重復(fù)應(yīng)用 (convolution ->max-pool) 操作，使用 ReLU 作為卷積的激活函數(shù)。然后，將輸出量展平并將其送入兩個完全連接的層，最后是一個帶有 sigmoid 激活的單神經(jīng)元層，產(chǎn)生一個介于 0 和 1 之間的輸出，它表明模型是預(yù)測貓（0）還是 狗 (1).

訓(xùn)練：使用學(xué)習(xí)率為 0.01 的 SGD。一直訓(xùn)練到驗(yàn)證損失在 100 次迭代中都沒有改善為止。

Batch Size如何影響訓(xùn)練？

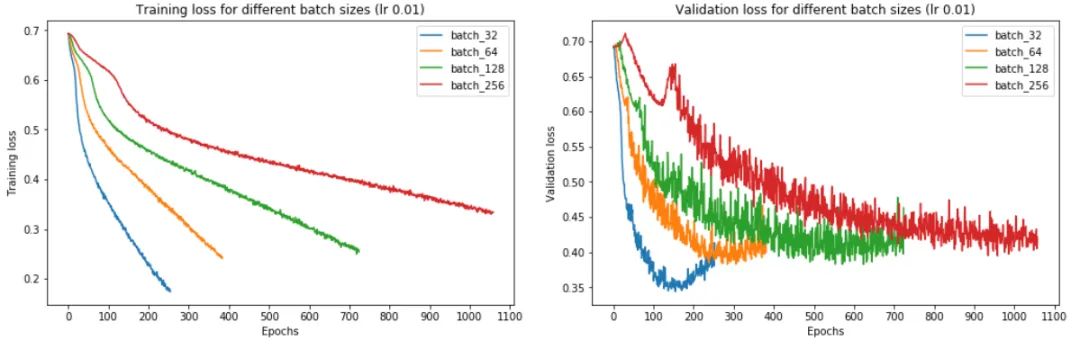
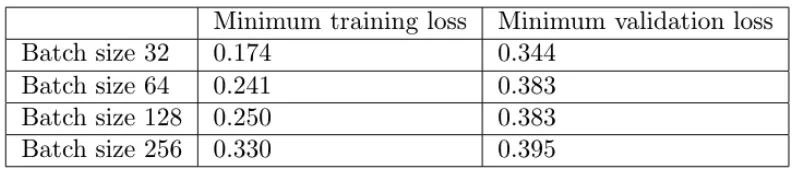
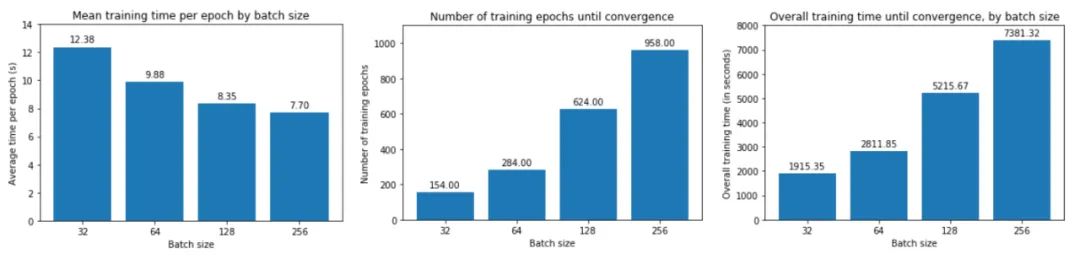
從上圖中，我們可以得出結(jié)論，batch size越大：

• 訓(xùn)練損失減少的越慢。

• 最小驗(yàn)證損失越高。

• 每個時期訓(xùn)練所需的時間越少。

• 收斂到最小驗(yàn)證損失所需的 epoch 越多。

讓我們一一了解這些。首先，在大批量訓(xùn)練中，訓(xùn)練損失下降得更慢，如紅線（批量大小 256）和藍(lán)線（批量大小 32）之間的斜率差異所示。

其次，大批量訓(xùn)練比小批量訓(xùn)練實(shí)現(xiàn)更糟糕的最小驗(yàn)證損失。例如，批量大小為 256 的最小驗(yàn)證損失為 0.395，而批量大小為 32 時為 0.344。

第三，大批量訓(xùn)練的每個 epoch 花費(fèi)的時間略少——批量大小 256 為 7.7 秒，而批量大小 256 為 12.4 秒，這反映了與加載少量大批量相關(guān)的開銷較低，而不是許多小批量依次。如果我們使用多個 GPU 進(jìn)行并行訓(xùn)練，這種時間差異會更加明顯。

然而，大批量訓(xùn)練需要更多的 epoch 才能收斂到最小值——批量大小 256 為 958，批量大小 32 為 158。因此，大批量訓(xùn)練總體上花費(fèi)的時間更長：批量大小 256 花費(fèi)的時間幾乎是 32 的四倍！請注意，我們沒有在這里并行化訓(xùn)練——如果我們這樣做了，那么大批量訓(xùn)練的訓(xùn)練速度可能與小批量訓(xùn)練一樣快。

如果我們并行化訓(xùn)練運(yùn)行會發(fā)生什么？為了回答這個問題，我們使用 TensorFlow 中的 MirroredStrategy 在四個 GPU 上并行訓(xùn)練：

with tf.distribute.MirroredStrategy().scope():   # Create, compile, and fit model   # ...

MirroredStrategy 將模型的所有變量復(fù)制到每個 GPU，并將前向/后向傳遞計算批量分發(fā)到所有 GPU。然后，它使用 all-reduce 組合來自每個 GPU 的梯度，然后將結(jié)果應(yīng)用于每個 GPU 的模型副本。本質(zhì)上，它正在劃分批次并將每個塊分配給 GPU。

我們發(fā)現(xiàn)并行化使每個 epoch 的小批量訓(xùn)練速度稍慢，而它使大批量訓(xùn)練速度更快——對于 256 批大小，每個 epoch 需要 3.97 秒，低于 7.70 秒。然而，即使有 per-epoch 加速，它也無法在總訓(xùn)練時間方面匹配批量大小 32——當(dāng)我們乘以總訓(xùn)練時間 (958) 時，我們得到大約 3700 秒的總訓(xùn)練時間，即 仍然遠(yuǎn)大于批大小 32 的 1915 秒。

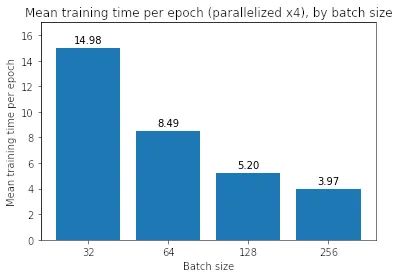
到目前為止，大批量訓(xùn)練看起來并不值得，因?yàn)樗鼈冃枰L的時間來訓(xùn)練，并且訓(xùn)練和驗(yàn)證損失更嚴(yán)重。 為什么會這樣？有什么辦法可以縮小性能差距嗎？

為什么較小的批量性能更好？

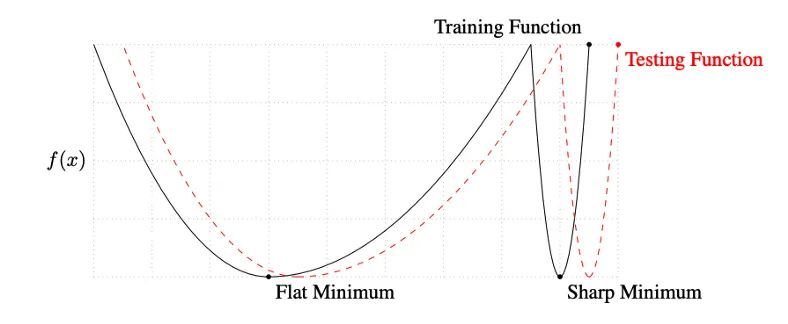
Keskar 等人對小批量和大批量之間的性能差距提出了一種解釋：使用小批量的訓(xùn)練傾向于收斂到平坦的極小化，該極小化在極小化的小鄰域內(nèi)僅略有變化，而大批量則收斂到尖銳的極小化，這變化很大。平面minimizers 傾向于更好地泛化，因?yàn)樗鼈儗τ?xùn)練集和測試集之間的變化更加魯棒 。

此外，他們發(fā)現(xiàn)與大批量訓(xùn)練相比，小批量訓(xùn)練可以找到距離初始權(quán)重更遠(yuǎn)的最小值。他們解釋說，小批量訓(xùn)練可能會為訓(xùn)練引入足夠的噪聲，以退出銳化minimizers 的損失池，而是找到可能更遠(yuǎn)的平坦minimizers 。

讓我們驗(yàn)證這些假設(shè)。

假設(shè) 1：與大批量最小化器相比，小批量minimizers 離初始權(quán)重更遠(yuǎn)。

我們首先測量初始權(quán)重和每個模型找到的最小值之間的歐幾里德距離。

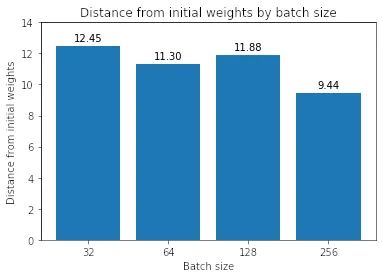
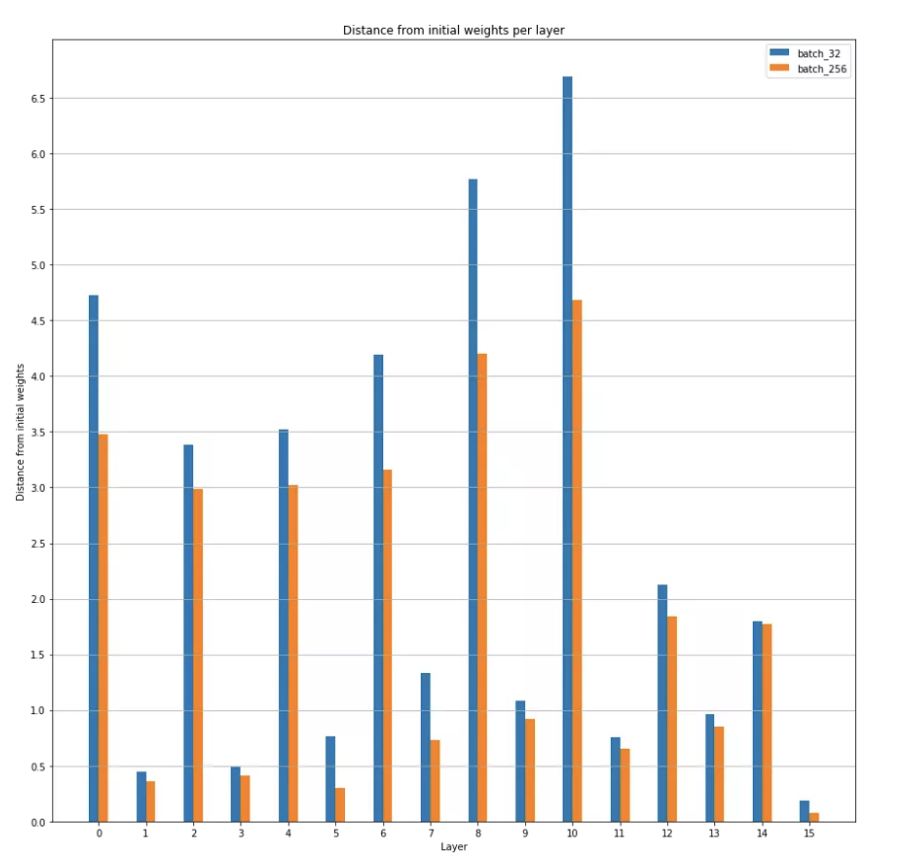
按層與初始權(quán)重的距離，批大小 32 和 256 的比較

事實(shí)上，我們發(fā)現(xiàn)一般來說，批量越大，最小值越接近初始權(quán)重。（除了批量大小 128 比批量大小 64 離初始權(quán)重更遠(yuǎn)）。我們還在圖 11 中看到，模型中的不同層都是如此。

為什么大批量訓(xùn)練最終更接近初始權(quán)重？是否采取較小的更新步驟？讓我們通過測量epoch距離——即epoch i 中的最終權(quán)重與epoch i 中的初始權(quán)重之間的距離——找出批量大小 32 和 256 的原因。

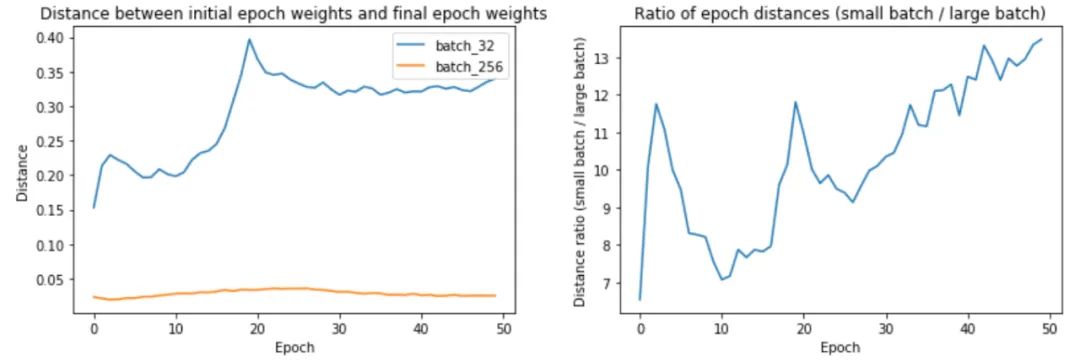
上面的第一幅圖顯示，較大的批次大小確實(shí)確實(shí)在每個 epoch 中遍歷的距離更短。第 32 批訓(xùn)練的 epoch 距離從 0.15 到 0.4 不等，而第 256 批訓(xùn)練的距離約為 0.02–0.04。事實(shí)上，正如我們在第二個圖中所看到的，epoch距離的比率隨著時間的推移而增加！

但是為什么大批量訓(xùn)練每個 epoch 遍歷的距離更短呢？是因?yàn)槲覀兊呐屋^少，因此每個 epoch 的更新較少嗎？還是因?yàn)槊看闻扛卤闅v的距離更短？或者，答案是兩者的結(jié)合？

為了回答這個問題，讓我們測量每個批量更新的大小。

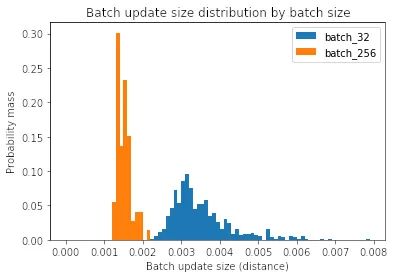
Median batch update norm for batch size 32: 3.3e-3Median batch update norm for batch size 256: 1.5e-3

我們可以看到，當(dāng)批大小較大時，每次批更新較小。為什么會這樣？

為了理解這種行為，讓我們設(shè)置一個虛擬場景，其中我們有兩個梯度向量 a 和 b，每個表示一個訓(xùn)練示例的梯度。讓我們考慮一下批量大小 = 1 的平均批量更新大小與批量大小 = 2 的情況相比如何。

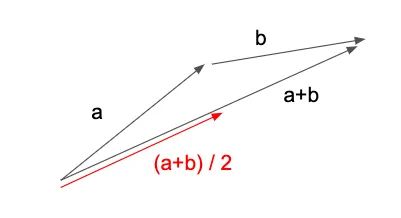
如果我們使用 1 的批量大小，我們將在 a 的方向上邁出一步，然后是 b，最終在 a+b 表示的點(diǎn)上。（從技術(shù)上講，b 的梯度將在應(yīng)用 a 后重新計算，但我們現(xiàn)在先忽略它）。這導(dǎo)致平均批量更新大小為 (|a|+|b|)/2 — 批量更新大小的總和除以批量更新的數(shù)量。

但是，如果我們使用批量大小為 2，批量更新將改為由向量 (a+b)/2 表示 — 圖 12 中的紅色箭頭。因此，平均批量更新大小為 |(a+b)/ 2| / 1 = |a+b|/2。

現(xiàn)在，讓我們比較兩個平均批量更新大小：

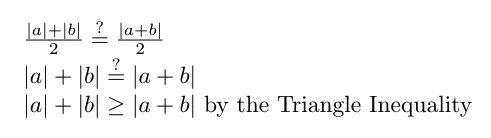
在最后一行中，我們使用三角不等式來表明批量大小 1 的平均批量更新大小始終大于或等于批量大小 2 的平均批量更新大小。

換句話說，為了使批量大小 1 和批量大小 2 的平均批量大小相等，向量 a 和 b 必須指向相同的方向，因?yàn)槟鞘?|a| 的時候。+ |b| = |a+b|。我們可以將此參數(shù)擴(kuò)展到 n 個向量——只有當(dāng)所有 n 個向量都指向同一方向時，batch size=1 和 batch size=n 的平均批量更新大小才相同。然而，這幾乎從來都不是這樣的，因?yàn)樘荻认蛄坎惶赡苤赶蛲耆嗤姆较颉?/p>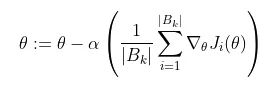

如果我們回到圖 16 中的小批量更新方程，我們在某種意義上說，當(dāng)我們擴(kuò)大批量大小 |B_k| 時，梯度總和的大小相對較慢地擴(kuò)大。這是因?yàn)樘荻认蛄恐赶虿煌姆较颍虼藢⑴看笮。匆釉谝黄鸬奶荻认蛄康臄?shù)量）加倍并不會使生成的梯度向量總和的大小加倍。同時，我們除以分母 |B_k|這是兩倍大，導(dǎo)致整體更新步驟更小。

這可以解釋為什么更大批量的批量更新往往更小——梯度向量的總和變得更大，但不能完全抵消更大的分母|B_k|。

假設(shè) 2：小批量訓(xùn)練找到更平坦的最小值

現(xiàn)在讓我們測量兩個minimizers的銳度，并評估小批量訓(xùn)練找到更平坦的minimizers的說法。（請注意，第二個假設(shè)可以與第一個假設(shè)共存——它們并不相互排斥。）為此，我們從 Keskar 等人那里借用了兩種方法。

在第一個中，我們沿著小批量minimizers（批量大小 32）和大批量minimizers（批量大小 256）之間的線繪制訓(xùn)練和驗(yàn)證損失。這條線由以下等式描述：

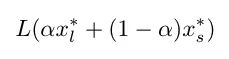
其中 x_l* 是大批量minimizers，x_s* 是小批量minimizers，alpha 是一個介于 -1 和 2 之間的系數(shù)。

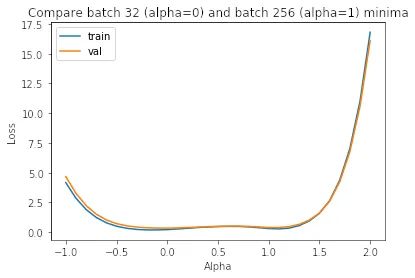
正如我們在圖中所見，小批量minimizers (alpha=0) 比大批量minimizers (alpha=1) 平坦得多，后者的變化更加劇烈。

請注意，這是一種相當(dāng)簡單的銳度測量方法，因?yàn)樗豢紤]一個方向。因此，Keskar 等人提出了一個銳度度量，用于衡量損失函數(shù)在最小值附近的鄰域內(nèi)的變化程度。首先，我們定義鄰域如下：

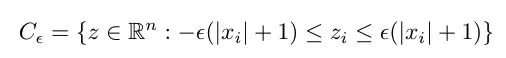
其中 epsilon 是定義鄰域大小的參數(shù)，x 是最小值（權(quán)重）。

然后，我們將銳度度量定義為最小值附近的最大損失：

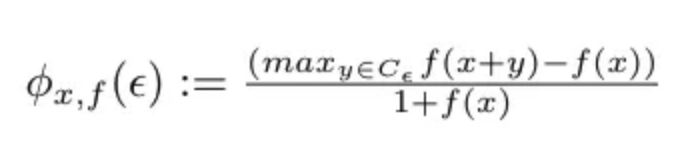
其中 f 是損失函數(shù)，輸入是權(quán)重。

使用上面的定義，讓我們計算各種批量大小下的最小化器的銳度，epsilon 值為 1e-3：

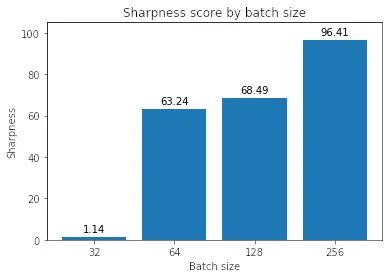
這表明大批量最小化器確實(shí)更清晰，正如我們在插值圖中看到的那樣。

最后，讓我們嘗試用 Li 等人制定的過濾器歸一化損失可視化來繪制最小化器。這種類型的圖選擇兩個與模型權(quán)重具有相同維度的隨機(jī)方向，然后將每個卷積濾波器（或神經(jīng)元，在 FC 層的情況下）歸一化為與模型權(quán)重中的相應(yīng)濾波器具有相同的范數(shù)。這確保了最小化器的銳度不受其權(quán)重大小的影響。然后，它沿著這兩個方向繪制損失，圖的中心是我們希望表征的最小值。

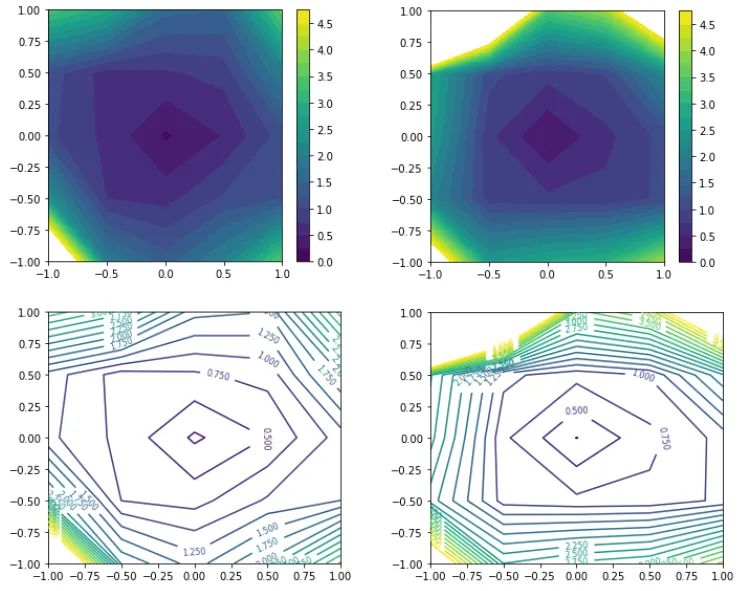
同樣，我們可以從等高線圖中看到，對于大批量最小化器，損失變化更加劇烈。

通過提高學(xué)習(xí)率可以提高大批量的性能嗎

在假設(shè) 1 中，我們看到大批量的更新大小和每個 epoch 的更新頻率都較低，而在假設(shè) 2 中，我們看到大批量無法探索與小批量一樣大的區(qū)域。知道了這一點(diǎn)，我們是否可以通過簡單地提高學(xué)習(xí)率來使大批量訓(xùn)練表現(xiàn)更好？

這種方法以前曾被建議過，例如 Goyal 等人提出：“線性縮放規(guī)則：當(dāng) minibatch 大小乘以 k 時，將學(xué)習(xí)率乘以 k。”

讓我們試試這個，批量大小為 32、64、128 和 256。我們將對批量大小 32 使用 0.01 的基本學(xué)習(xí)率，并相應(yīng)地縮放其他批量大小。

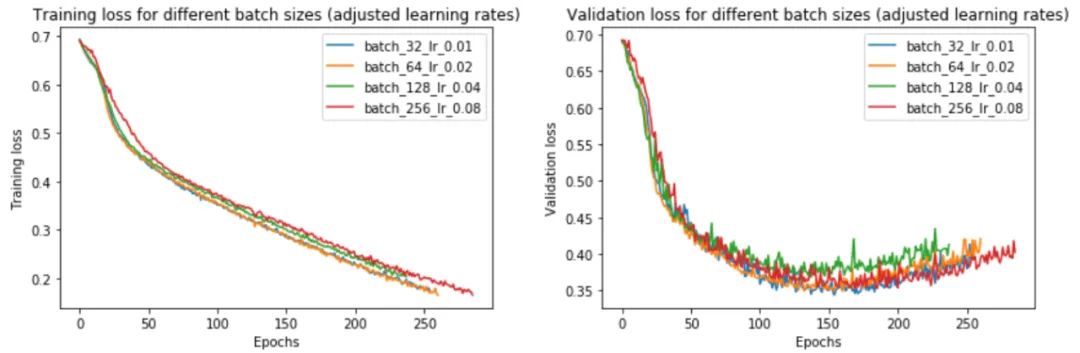
事實(shí)上，我們發(fā)現(xiàn)調(diào)整學(xué)習(xí)率確實(shí)消除了小批量和大批量之間的大部分性能差距。現(xiàn)在，批量大小 256 的驗(yàn)證損失為 0.352 而不是 0.395——更接近批量大小 32 的損失 0.345。

提高學(xué)習(xí)率如何影響訓(xùn)練時間？由于大批量訓(xùn)練現(xiàn)在可以在與小批量訓(xùn)練大致相同的迭代次數(shù)中收斂，如圖 25 中的左圖所示，現(xiàn)在總體訓(xùn)練時間更短——批量大小 256 為 2197 秒，而批量為 3156 大小為 32。如果我們跨 4 個 GPU 并行化，則加速更加明顯。

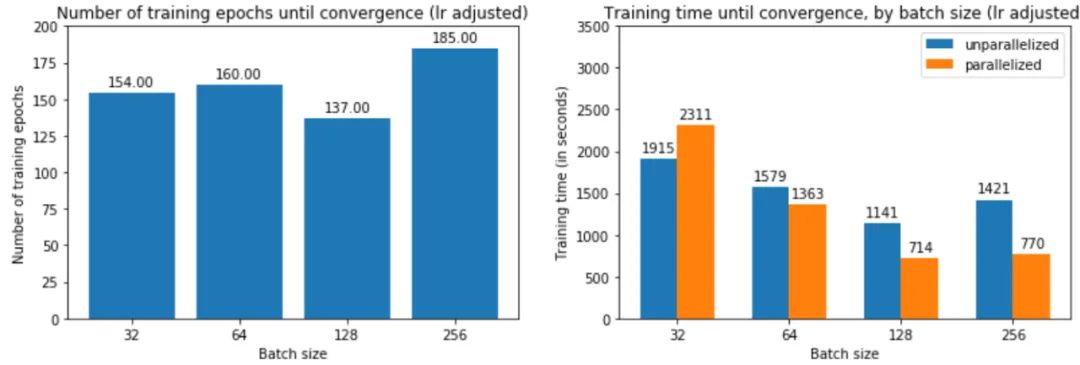
這是否意味著大批量現(xiàn)在正在收斂到平面minimizers？如果我們繪制銳度分?jǐn)?shù)，我們可以看到調(diào)整學(xué)習(xí)率確實(shí)使大批量最小化器更平坦：

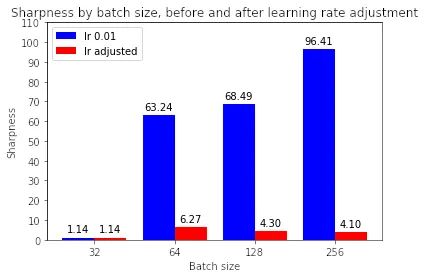
有趣的是，雖然調(diào)整學(xué)習(xí)率使大批量minimizers更平坦，但它們?nèi)匀槐茸钚∨孔钚』鞲J利（4-7 與 1.14 相比）。為什么會這樣仍然是未來調(diào)查的問題。

較大批量的訓(xùn)練運(yùn)行現(xiàn)在是否與小批量的初始權(quán)重相差甚遠(yuǎn)？

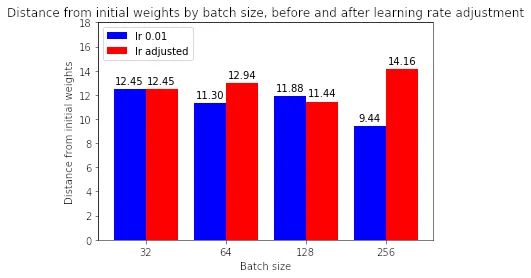
大多數(shù)情況下，答案是肯定的。如果我們看上面的圖，調(diào)整學(xué)習(xí)率有助于縮小批量大小 32 與其他批量大小之間在與初始權(quán)重的距離方面的差距。（請注意，128 似乎是一個異常，其中增加學(xué)習(xí)率會降低距離——為什么會出現(xiàn)這種情況，有待未來調(diào)查。）

小批量訓(xùn)練總是優(yōu)于大批量訓(xùn)練嗎？

鑒于上述觀察和文獻(xiàn)，如果我們保持學(xué)習(xí)率不變，我們可能會期望小批量訓(xùn)練總是優(yōu)于大批量訓(xùn)練。事實(shí)上，事實(shí)并非如此，正如我們在使用學(xué)習(xí)率 0.08 時所看到的：

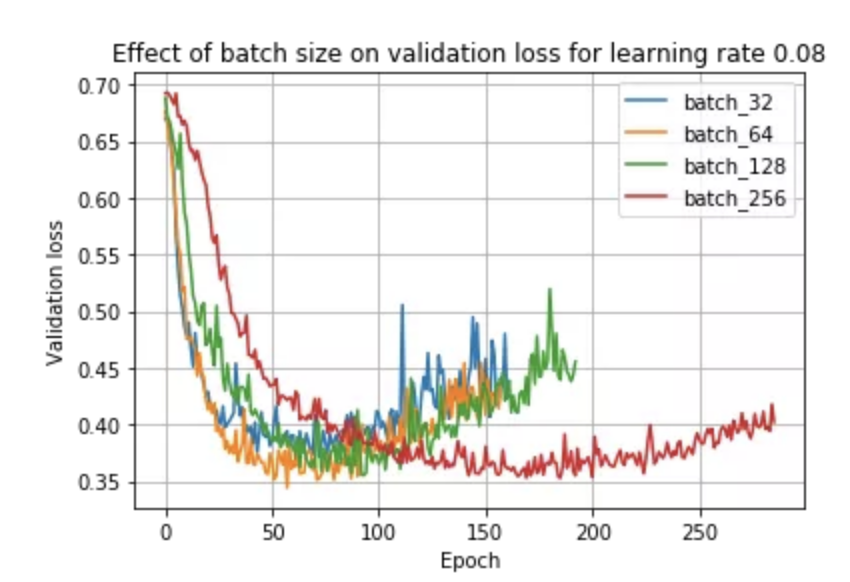
在這里，我們看到批量大小 64 實(shí)際上優(yōu)于批量大小 32！這是因?yàn)閷W(xué)習(xí)率和批量大小密切相關(guān)——小批量在較小的學(xué)習(xí)率下表現(xiàn)最好，而大批量在較大的學(xué)習(xí)率下表現(xiàn)最好。我們可以在下面看到這種現(xiàn)象：

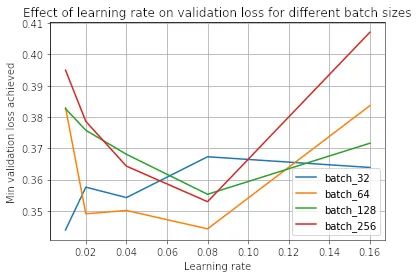
我們看到，0.01 的學(xué)習(xí)率對于批大小 32 是最好的，而 0.08 對于其他批大小是最好的。

因此，如果您注意到大批量訓(xùn)練在相同學(xué)習(xí)率下優(yōu)于小批量訓(xùn)練，這可能表明學(xué)習(xí)率大于小批量訓(xùn)練的最佳值。

結(jié)論

那么，這意味著什么？我們可以從這些實(shí)驗(yàn)中得到什么？

線性縮放規(guī)則：當(dāng) minibatch 大小乘以 k 時，將學(xué)習(xí)率乘以 k。盡管我們最初發(fā)現(xiàn)大批量性能更差，但我們能夠通過提高學(xué)習(xí)率來縮小大部分差距。我們看到這是由于較大的批次大小應(yīng)用了較小的批次更新，這是由于批次內(nèi)梯度向量之間的梯度競爭。

選擇合適的學(xué)習(xí)率時，較大的批量尺寸可以更快地訓(xùn)練，特別是在并行化時。對于大批量，我們不受 SGD 更新的順序性質(zhì)的限制，因?yàn)槲覀儾粫龅脚c將許多小批量順序加載到內(nèi)存中相關(guān)的開銷。我們還可以跨訓(xùn)練示例并行化計算。

然而，當(dāng)學(xué)習(xí)率沒有針對較大的批量大小向上調(diào)整時，大批量訓(xùn)練可能比小批量訓(xùn)練花費(fèi)的時間更長，因?yàn)樗枰嗟挠?xùn)練時期來收斂。因此，您需要調(diào)整學(xué)習(xí)率以實(shí)現(xiàn)更大批量和并行化的加速。

大批量，即使調(diào)整了學(xué)習(xí)率，在我們的實(shí)驗(yàn)中表現(xiàn)稍差，但需要更多的數(shù)據(jù)來確定更大的批量是否總體上表現(xiàn)更差。我們?nèi)匀挥^察到最小批量大小（val loss 0.343）和最大批量大小（val loss 0.352）之間的輕微性能差距。一些人認(rèn)為小批量具有正則化效果，因?yàn)樗鼈儗⒃肼曇敫拢瑤椭?xùn)練擺脫次優(yōu)局部最小值的吸引力 。然而，這些實(shí)驗(yàn)的結(jié)果表明，性能差距相對較小，至少對于這個數(shù)據(jù)集。這表明，只要您為批量大小找到合適的學(xué)習(xí)率，您就可以專注于可能對性能產(chǎn)生更大影響的其他方面的訓(xùn)練。

參考論文

1. Keskar, Nocedal, Mudigere, Smelyanskiy, and Tang. On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima. https://arxiv.org/pdf/1609.04836.pdf
2. Li, Xu, Taylor, Studer, and Goldstein. Visualizing the Loss Landscape of Neural Nets. https://papers.nips.cc/paper/7875-visualizing-the-loss-landscape-of-neural-nets.pdf.
3. Goyal, Dollar, Girshick, Noordhuis, Wesolowski, Kyrola, Tulloch, Jia, and He. Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour. https://research.fb.com/wp-content/uploads/2017/06/imagenet1kin1h5.pdf.

如果覺得有用，就請分享到朋友圈吧！