深度學(xué)習(xí)以及卷積基礎(chǔ)
點(diǎn)擊上方“小白學(xué)視覺”,選擇加"星標(biāo)"或“置頂”
重磅干貨,第一時間送達(dá)
作者:石文華
編輯:龔? ?賽
介? ? 紹
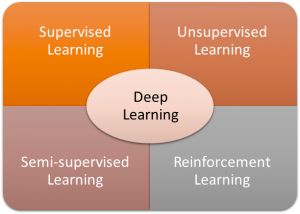
深度學(xué)習(xí)是機(jī)器學(xué)習(xí)的一個分支,是基于數(shù)據(jù)來學(xué)習(xí)表示數(shù)據(jù)的一組算法。下面我們列出最受歡迎的一些深度學(xué)習(xí)算法。
卷積神經(jīng)網(wǎng)絡(luò)
深度信念網(wǎng)絡(luò)
自動編碼器
遞歸神經(jīng)網(wǎng)絡(luò)(RNN / LSTM / GRU)
對抗生成網(wǎng)絡(luò)(GAN)?
深度學(xué)習(xí)的目的之一是他們將取代手工制作的特征提取。這個想法是,他們將從給定的數(shù)據(jù)中“學(xué)習(xí)”到所需的最佳特征。?
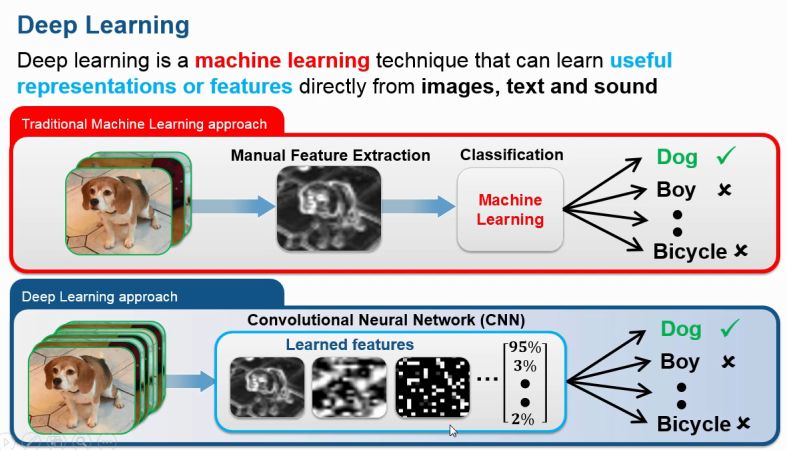
層與層
深度學(xué)習(xí)模型由多層構(gòu)成,在人工神經(jīng)網(wǎng)絡(luò)的情況下,具有2個以上隱藏層的多層感知器(MLP)已經(jīng)是深度模型。?
作為一個經(jīng)驗(yàn)法則,深層模型有可能比淺層模型表現(xiàn)更好。但是,越深的神經(jīng)網(wǎng)絡(luò)你需要越多的數(shù)據(jù)來避免過擬合。?
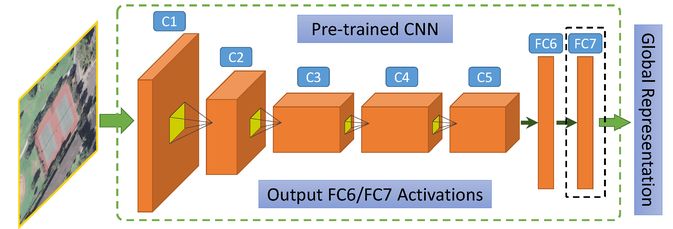
層類型
卷積層?
最大/平均池化層?
Dropout層?
批量標(biāo)準(zhǔn)化層?
全連接層?
Relu,Tanh,Sigmoid層(非線性層)?
Softmax,交叉熵,SVM,歐幾里得(損失層)
避免過擬合(正則化)
除了獲得更多的數(shù)據(jù)之外,還有一些技巧用于解決過度擬合問題,這里列出了一些最常見的技術(shù):
Dropout
L2正則化
數(shù)據(jù)增強(qiáng)
Dropout
這是一種在訓(xùn)練期間隨機(jī)關(guān)閉全連接層中一些神經(jīng)元的技術(shù)。?
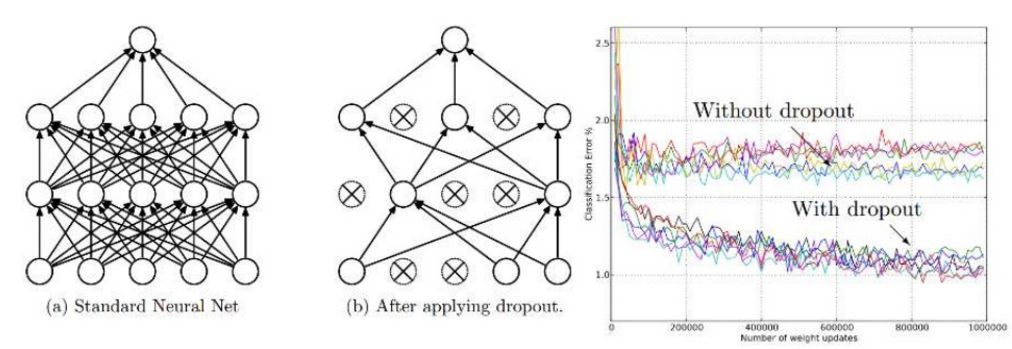
Dropout迫使全連接層以不同的方式學(xué)習(xí)相同的概念。
L2正則化
最常見的正則化形式是L2正則化,L2正則化是給損失函數(shù)添加一個額外的懲罰項(xiàng),這個懲罰項(xiàng)也就是我們正在優(yōu)化的所有權(quán)重/參數(shù)的平方值。對于神經(jīng)網(wǎng)絡(luò)的每一個參數(shù)ω,我們加入一項(xiàng)0.5λω2到損失函數(shù)中去,λ表示正則化強(qiáng)度的參數(shù),當(dāng)我們反向傳播計算導(dǎo)數(shù)時,我們只是用了0.5λ作為正則化的強(qiáng)度。由于使用這種正規(guī)化,非常高價值的權(quán)重受到嚴(yán)重懲罰。所以我們更傾向于使用一層的所有權(quán)重作為輸入,而不是少數(shù)一些權(quán)重帶替代。這種方法的效果比較好,因?yàn)槲覀兊哪P蜋?quán)重將被最大限度地利用,并且我們有更少未使用的權(quán)重。
除了L2正則化之外,還有L1正則化和Max Norm,但這里沒有討論,因?yàn)長2一般表現(xiàn)更好。
數(shù)據(jù)增強(qiáng)
通過對輸入數(shù)據(jù)進(jìn)行一些轉(zhuǎn)換,可以合成新的訓(xùn)練樣例。例如,進(jìn)行圖像翻轉(zhuǎn)或隨機(jī)移動RGB值。在2012年Imagenet競賽期間,Alex Krizhevesky(Alexnet)使用了2048倍的因子進(jìn)行數(shù)據(jù)增強(qiáng),這意味著用于訓(xùn)練其模型的數(shù)據(jù)集實(shí)際上比開始時大2048倍,并且在不使用數(shù)據(jù)增強(qiáng)的情況下改進(jìn)了泛化。?


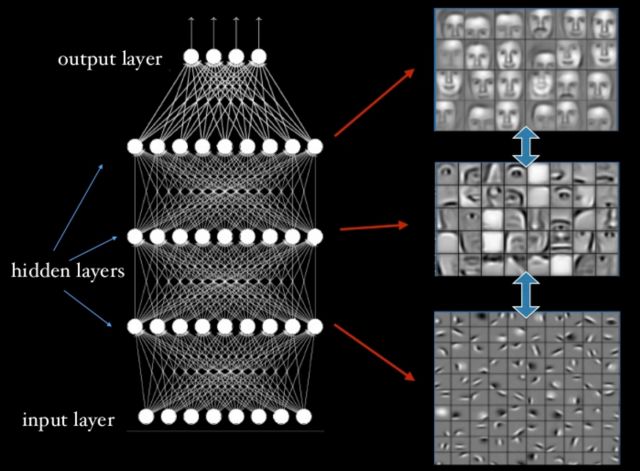
分層的特征表示
它是讓學(xué)習(xí)算法找到從輸入到更深層的最佳表示。?
淺層學(xué)會用簡單的形式表示數(shù)據(jù),深層用前面學(xué)到的特征來學(xué)習(xí)更高緯度的特征來表示數(shù)據(jù)。?

卷? 積
卷積是一種數(shù)學(xué)運(yùn)算,它對兩個函數(shù)(信號)乘積進(jìn)行積分,其中一個信號是被翻轉(zhuǎn)。例如下面我們對2個信號f(t)和g(t)進(jìn)行卷積。?

首先要做的是水平翻轉(zhuǎn)(180度)信號g,然后將翻轉(zhuǎn)后的g滑過f,對應(yīng)相乘并累加所有的值。?
conv(a,b)== conv(b,a)的結(jié)果是一樣的,?
在這種情況下,規(guī)定藍(lán)色信號 F(τ)F(τ) 是我們的輸入信號和 G(t )G(?) 作為我們的卷積核,當(dāng)使用卷積來過濾信號時使用術(shù)語卷積核。
輸出一維信號
在一維卷積的情況下,輸出尺寸計算如下:?
outputSize=(InputSize?KernelSize)+1
卷積的應(yīng)用
人們在以下用例中對信號處理使用卷積:
濾波器信號(1D音頻,2D圖像處理)
檢查一個信號與另一個信號的相關(guān)程度
在信號中查找模式
在matlab和python(numpy)中的簡單例子
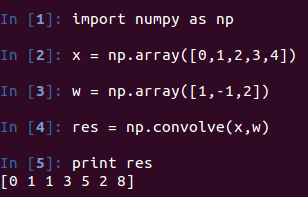
下面我們將兩個信號x =(0,1,2,3,4)與w =(1,-1,2)進(jìn)行卷積。?

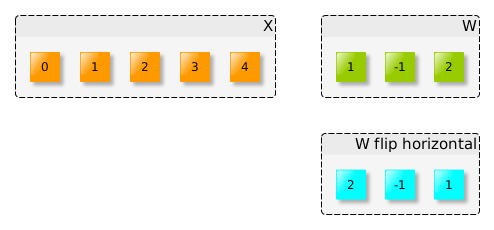
手工操作
為了更好地理解卷積的概念,我們手工完成上面的例子。我們要卷積2個信號(x,w)。首先是水平翻轉(zhuǎn)W(或向左旋轉(zhuǎn)180度)?
之后,我們將翻轉(zhuǎn)的W滑過輸入X.?
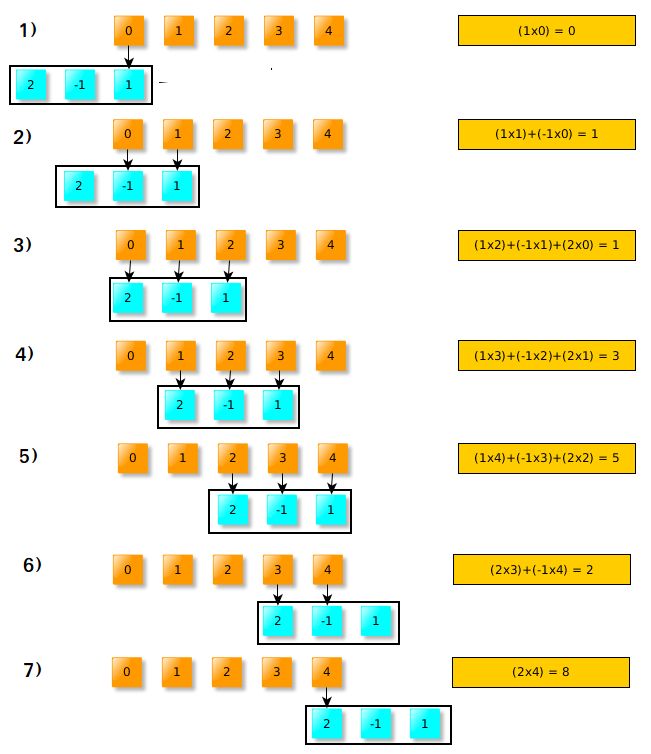
注意到在步驟3,4,5中,翻轉(zhuǎn)后的窗口完全位于輸入信號的內(nèi)部。稱為“有效”卷積。在翻轉(zhuǎn)窗口不完全位于輸入窗口(X)內(nèi)部的情況下,我們可以將其視為零,只計算位于窗口內(nèi)的數(shù)據(jù),例如在步驟1中,我們將1乘以零,其余部分將被忽略。
對輸入進(jìn)行填充
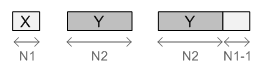
為了保持卷積結(jié)果大小與輸入大小相同,并避免稱為循環(huán)卷積的效應(yīng),我們用零填充信號。?
你把零放在哪個位置取決于你想要做什么,例如:在1D的情況下,你可以在每一端連接它們,但在2D上它通常放置在原始信號周圍。?
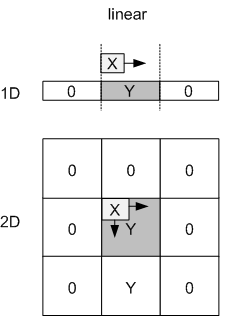
在matlab上,你可以使用命令'padarray'來填充輸入信號:?
>> x
x(:,:,1) =
1 ? ? 1 ? ? 0 ? ? 2 ? ? 0
2 ? ? 2 ? ? 2 ? ? 2 ? ? 1
0 ? ? 0 ? ? 0 ? ? 2 ? ? 1
2 ? ? 2 ? ? 2 ? ? 2 ? ? 1
2 ? ? 0 ? ? 2 ? ? 2 ? ? 1x(:,:,2) =
2 ? ? 1 ? ? 0 ? ? 0 ? ? 0
0 ? ? 2 ? ? 0 ? ? 1 ? ? 0
1 ? ? 0 ? ? 1 ? ? 2 ? ? 0
1 ? ? 2 ? ? 0 ? ? 2 ? ? 1
1 ? ? 2 ? ? 1 ? ? 2 ? ? 2x(:,:,3) =
2 ? ? 1 ? ? 1 ? ? 2 ? ? 2
1 ? ? 1 ? ? 1 ? ? 0 ? ? 0
2 ? ? 0 ? ? 1 ? ? 0 ? ? 2
0 ? ? 2 ? ? 0 ? ? 2 ? ? 1
0 ? ? 0 ? ? 2 ? ? 1 ? ? 0>> padarray(x,[1 1])
ans(:,:,1) =
0 ? ? 0 ? ? 0 ? ? 0 ? ? 0 ? ? 0 ? ? 0
0 ? ? 1 ? ? 1 ? ? 0 ? ? 2 ? ? 0 ? ? 0
0 ? ? 2 ? ? 2 ? ? 2 ? ? 2 ? ? 1 ? ? 0
0 ? ? 0 ? ? 0 ? ? 0 ? ? 2 ? ? 1 ? ? 0
0 ? ? 2 ? ? 2 ? ? 2 ? ? 2 ? ? 1 ? ? 0
0 ? ? 2 ? ? 0 ? ? 2 ? ? 2 ? ? 1 ? ? 0
0 ? ? 0 ? ? 0 ? ? 0 ? ? 0 ? ? 0 ? ? 0ans(:,:,2) =
0 ? ? 0 ? ? 0 ? ? 0 ? ? 0 ? ? 0 ? ? 0
0 ? ? 2 ? ? 1 ? ? 0 ? ? 0 ? ? 0 ? ? 0
0 ? ? 0 ? ? 2 ? ? 0 ? ? 1 ? ? 0 ? ? 0
0 ? ? 1 ? ? 0 ? ? 1 ? ? 2 ? ? 0 ? ? 0
0 ? ? 1 ? ? 2 ? ? 0 ? ? 2 ? ? 1 ? ? 0
0 ? ? 1 ? ? 2 ? ? 1 ? ? 2 ? ? 2 ? ? 0
0 ? ? 0 ? ? 0 ? ? 0 ? ? 0 ? ? 0 ? ? 0ans(:,:,3) =
0 ? ? 0 ? ? 0 ? ? 0 ? ? 0 ? ? 0 ? ? 0
0 ? ? 2 ? ? 1 ? ? 1 ? ? 2 ? ? 2 ? ? 0
0 ? ? 1 ? ? 1 ? ? 1 ? ? 0 ? ? 0 ? ? 0
0 ? ? 2 ? ? 0 ? ? 1 ? ? 0 ? ? 2 ? ? 0
0 ? ? 0 ? ? 2 ? ? 0 ? ? 2 ? ? 1 ? ? 0
0 ? ? 0 ? ? 0 ? ? 2 ? ? 1 ? ? 0 ? ? 0
0 ? ? 0 ? ? 0 ? ? 0 ? ? 0 ? ? 0 ? ? 0將卷積轉(zhuǎn)化為計算圖
將操作轉(zhuǎn)化為計算圖,更容易計算每個節(jié)點(diǎn)參數(shù)的偏導(dǎo)數(shù),這里我們演示將之前的一維卷積轉(zhuǎn)化為計算圖,這也可以擴(kuò)展到二維卷積。?
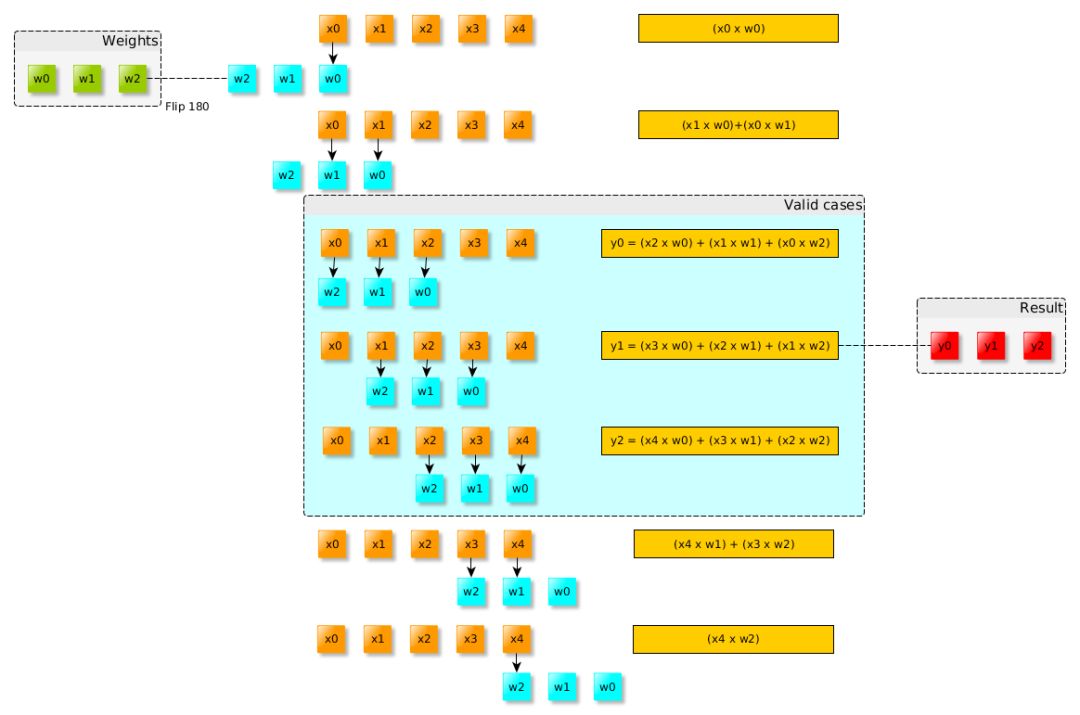
計算圖的創(chuàng)建是在翻轉(zhuǎn)的內(nèi)核完全插入被卷積的數(shù)據(jù)之前的。?
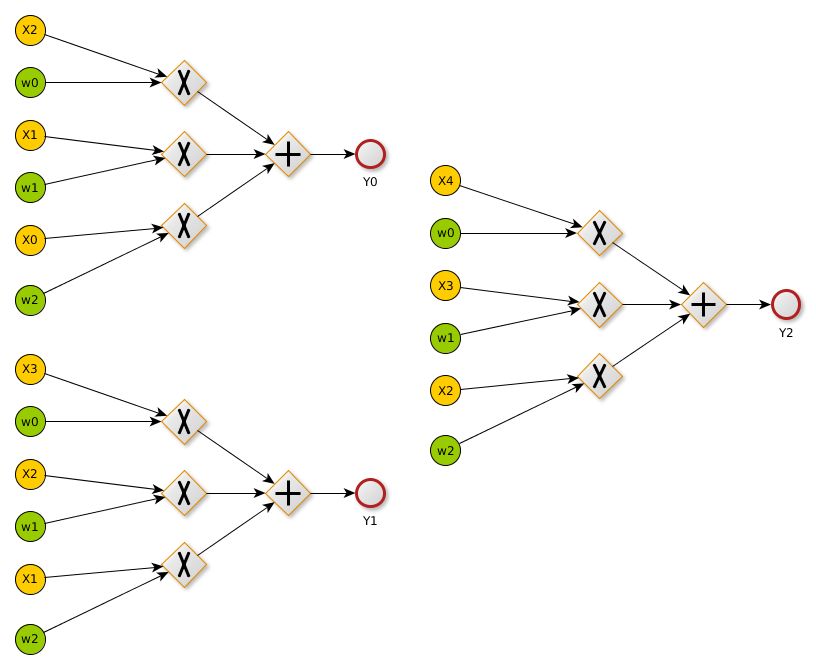
之后我們將使用這個圖來推斷卷積層的輸入(x)和權(quán)重(w)的梯度。
2D卷積
現(xiàn)在我們延伸到第二個維度。2D卷積被用作圖像濾波器。下面是一個2D圖像卷積的例子:?

Matlab與Python示例
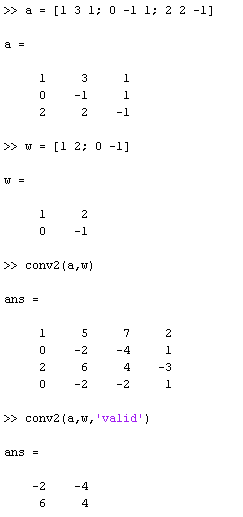
手工操作
首先,我們應(yīng)該翻轉(zhuǎn)內(nèi)核,然后在輸入信號上滑動內(nèi)核。?


步? 長
默認(rèn)情況下,當(dāng)我們進(jìn)行卷積運(yùn)算時,我們的窗口每次移動一個像素(步幅= 1),但是在卷積神經(jīng)網(wǎng)絡(luò)中我們需要移動多個像素。例如,在使用大小為2的內(nèi)核進(jìn)行卷積時,我們將使用2的步幅。將步幅和內(nèi)核大小都設(shè)置為2將導(dǎo)致輸出沿著兩個維度恰好為輸入大小的一半。?
觀察紅色內(nèi)核窗口下方的移動遠(yuǎn)遠(yuǎn)多于一個像素。?
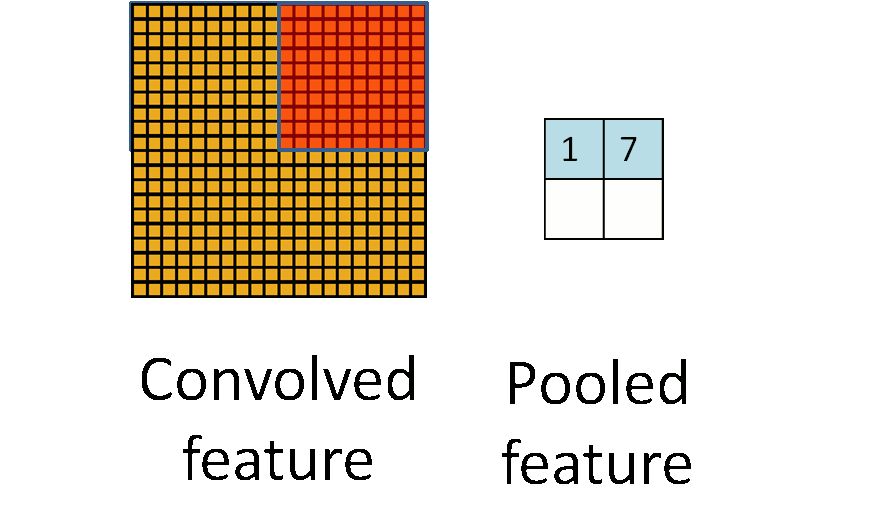
2D的輸出尺寸
下面提供了一個公式計算我們卷積之后的輸出尺寸 。
如果我們考慮將由P填充的空間大小[H,W]的輸入與大小為F的方形核并使用步長S進(jìn)行卷積,那么卷積的輸出大小被定義為:?
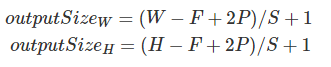
F是內(nèi)核的大小,通常我們使用方形內(nèi)核,所以F既是內(nèi)核的寬度又是高度。
實(shí)現(xiàn)卷積運(yùn)算
下面的示例將對一個5x5x3的輸入進(jìn)行卷積,其中具有以下參數(shù)Stride=2,Pad=1,F(xiàn)=3(3x3內(nèi)核)和K=2(兩個濾波器)的conv層。?
我們的輸入有3個通道,所以需要3x3x3的內(nèi)核權(quán)重。有2個過濾器(K = 2),所以最后會有2個輸出。計算這兩個輸出的大小為:(5 - 3 + 2)/ 2 + 1 = 3。得到最終的尺寸(3x3x2)。
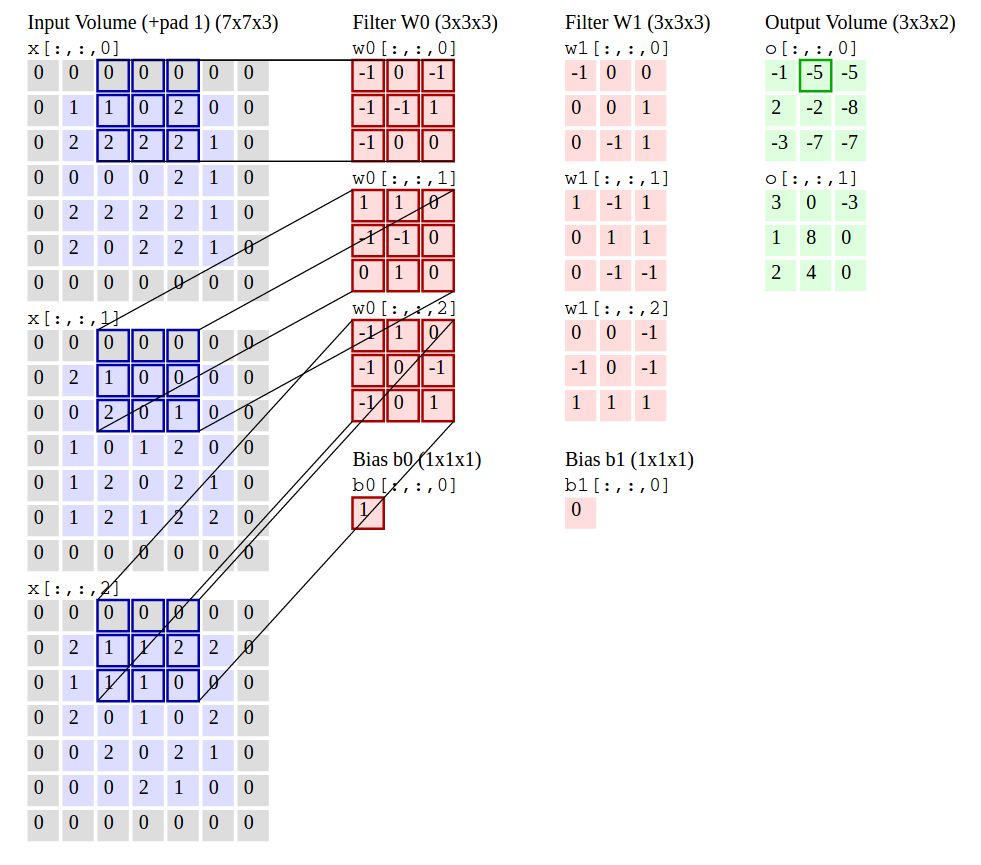
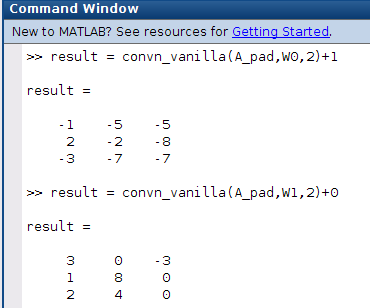
仔細(xì)看看這個例子,我們需要計算2個卷積,不要忘了給每個3x3x3濾波器(w0,w1)添加偏差。
參考文獻(xiàn)
https://en.wikipedia.org/wiki/Convolution
https://www.khanacademy.org/math/differential-equations/laplace-transform/convolution-integral/v/introduction-to-the-convolution
http://www.dspguide.com/ch6/2.htm
交流群
歡迎加入公眾號讀者群一起和同行交流,目前有SLAM、三維視覺、傳感器、自動駕駛、計算攝影、檢測、分割、識別、醫(yī)學(xué)影像、GAN、算法競賽等微信群(以后會逐漸細(xì)分),請掃描下面微信號加群,備注:”昵稱+學(xué)校/公司+研究方向“,例如:”張三?+?上海交大?+?視覺SLAM“。請按照格式備注,否則不予通過。添加成功后會根據(jù)研究方向邀請進(jìn)入相關(guān)微信群。請勿在群內(nèi)發(fā)送廣告,否則會請出群,謝謝理解~

