計算機中有哪些令人拍案叫絕的設(shè)計?
大家好!
前天日本前首相安倍晉三在演講過程中遇刺,這可能會成為2022年世界政壇上最熱門的一個新聞,但是隨后美國居然下半旗哀悼這位「盟友」,讓人想起難道美國忘記了八十年前那場偷襲了嗎?網(wǎng)上也是眾說紛紜,但是咱不太關(guān)心政治,今天咱們談?wù)摰脑掝}跟政壇也沒有關(guān)系,但是今天這篇文章就從那場偷襲使用的飛機開始吧。
那場偷襲早在2001年已經(jīng)被拍攝成了電影——《珍珠港》,絕對是一部精彩的空戰(zhàn)電影。但是在觀影的過程中,你有沒有想過這個問題:二戰(zhàn)時期的飛機,在進行空戰(zhàn)過程中自己飛機射出的子彈難道不會擊中自己飛機的槳葉嗎?其實我小時候看這部電影就有這樣的疑問,直到后來我在大學(xué)學(xué)習了《機械原理》后,解其背后的原理后:

機槍射擊協(xié)調(diào)器:它是一戰(zhàn)中在盟軍中服役的荷蘭人安東尼·福克發(fā)明的,他把凸輪安裝在螺旋槳軸上面,凸輪的三個凸起與槳葉剛好錯開一個角度,當突起部分碰到金屬棒后,金屬棒后端連接的機槍發(fā)射裝置就會被激活,繼而完成子彈發(fā)射,反之,當槳葉與槍管形成一條直線時,機槍自動停止射擊。這個巧妙的設(shè)計完美地避開了戰(zhàn)斗機出現(xiàn)自殘的事故。
當時我知道它的原理后,反應(yīng)是這樣的:
臥槽,還有這種操作!
臥槽,這么簡單我怎么沒想到!
的確,讓人虎軀一震的發(fā)明往往看上去都非常簡單,而且你經(jīng)常會想,這么簡單,嗯,我怎么沒想到?
我還是那句話,簡單即是美,但是簡單往往比復(fù)雜困難得多。
其實計算機的設(shè)計也是一門藝術(shù)的博弈,我們今天聊的話題就是計算機補碼的運算,它看似簡單,但是這個設(shè)計也是精妙絕倫。
一,邏輯電路是如何計算加法的
1938年,香農(nóng)(這個人不用說了吧,計算機行業(yè)的人沒人沒聽過他吧)在麻省理工學(xué)院發(fā)表了那篇題為《繼電器和開關(guān)電路的符號分析》(A Symbolic Analysis of Relay and Switching Circuits)的著名碩士論文,這是一篇具有劃時代意義的論文,他在文中清晰地闡述:電子工程師可以運用布爾代數(shù)的所有工具去設(shè)計開關(guān)電路。也就是說邏輯運算居然可以用電路來進行實現(xiàn),隨后人們根據(jù)這一理論設(shè)計出了各種邏輯門(Logic Gate)來進行數(shù)據(jù)運算,后期的電子計算機的運算原理都是基于這一理論進行實現(xiàn)的,比如人們根據(jù)繼電器或者晶體管的特性,設(shè)計了異或門(關(guān)于異或運算的本質(zhì)請參考 如何通俗理解異或運算 ):
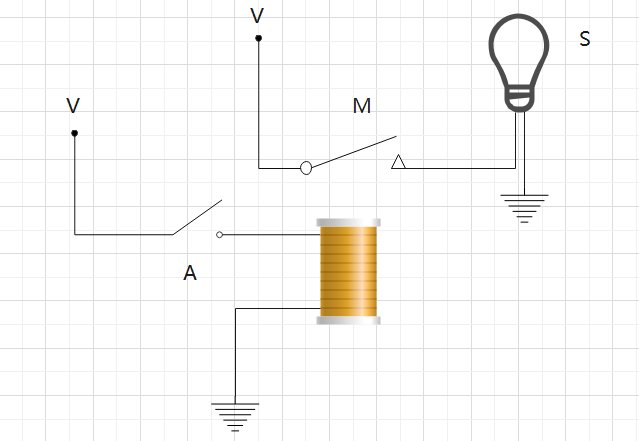
當開關(guān) A 閉合,線圈產(chǎn)生磁性將開關(guān) M 吸合,接通燈泡的回路,燈泡就會亮,這是一個最簡單的邏輯回路。你能想象人類發(fā)明CPU甚至所有的存儲設(shè)備其實就是這一堆堆開關(guān)組合成的嗎,雖然現(xiàn)代CPU用的是晶體管(速度更快、體積更小),但是原理都是一樣的。比如蘋果最新發(fā)布的M2芯片上面集成了200億個晶體管,翻譯成人話就是上面放了200億個開關(guān)。
這就像咱們老祖宗說的那句話,一生二,二生三,三生萬物。
后來人們根據(jù)上面那個電路進行簡單改造,無非就是開關(guān)的常開變常閉,或者常閉變常開等等,發(fā)明出了各種不同的邏輯門,可以實現(xiàn)更多的邏輯回路,比如與門(AND)、與非門(NAND)、或門(OR)、或非門(NOR)、異或門(XOR)等等。
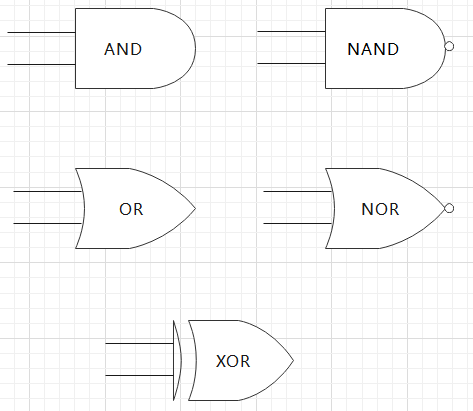
比如下面這個與門就是連個開關(guān)A與B必須同時閉合燈泡才能亮:
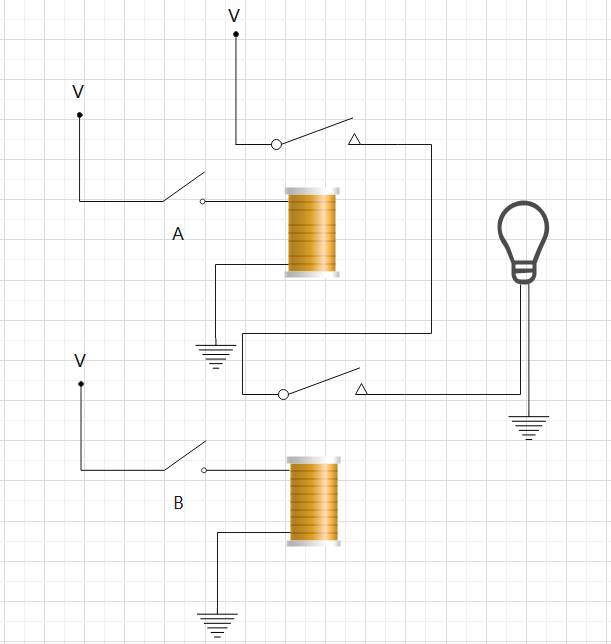
這樣的電路人們沒想到居然會與二進制的加法存在著某些聯(lián)系,比如二進制1+1=10的進位是1,而這個與門電路雙開關(guān)必須同時閉合才會亮,如果閉合代表1,斷開代表2,那么邏輯關(guān)系就是1 AND 1 = 1.
有一天,人們驚奇地發(fā)現(xiàn),一個異或門并聯(lián)一個與門居然能做簡單的二進制位的加法運算,給它命名叫半加器。之所以叫半加器,是因為它還沒有辦法將進位的輸出納入下一位的運算,比如 1+1=10,等號右邊的進位暫時還不能納入下一位的運算。
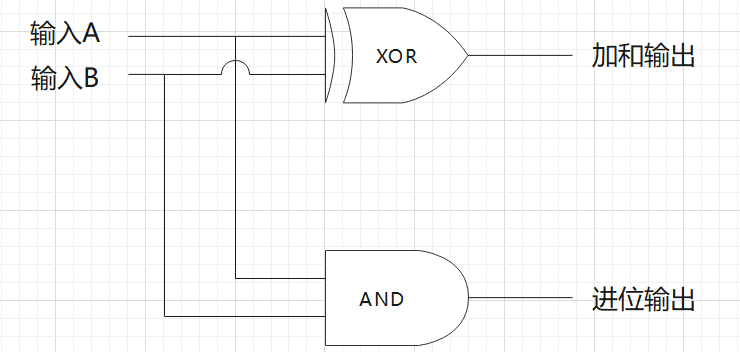
我們把這一堆符號合成一個整體:

半加器
后來,人們改進了這個電路,用兩個半加器再加一個或門,組成一個全加器,這次就厲害了,全加器彌補了半加器不能計算讓進位參與運算的缺點,可以將前一位的進位納入本位進行一塊計算,所以全加器輸入端有三個輸入:
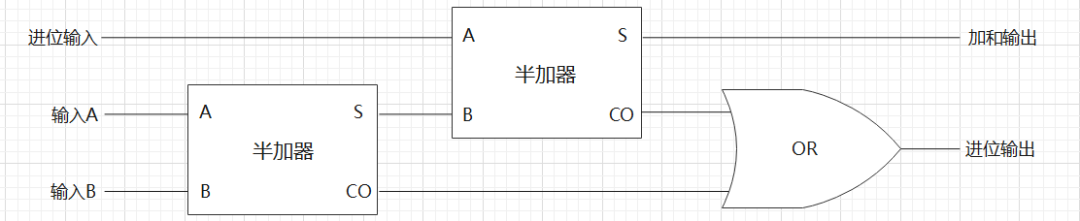
我們把上面這一堆符號合成一個整體:

全加器
多個全加器組合在一塊就能計算多位的二進制加法,下面這組加法器就能計算四位二進制的加法:
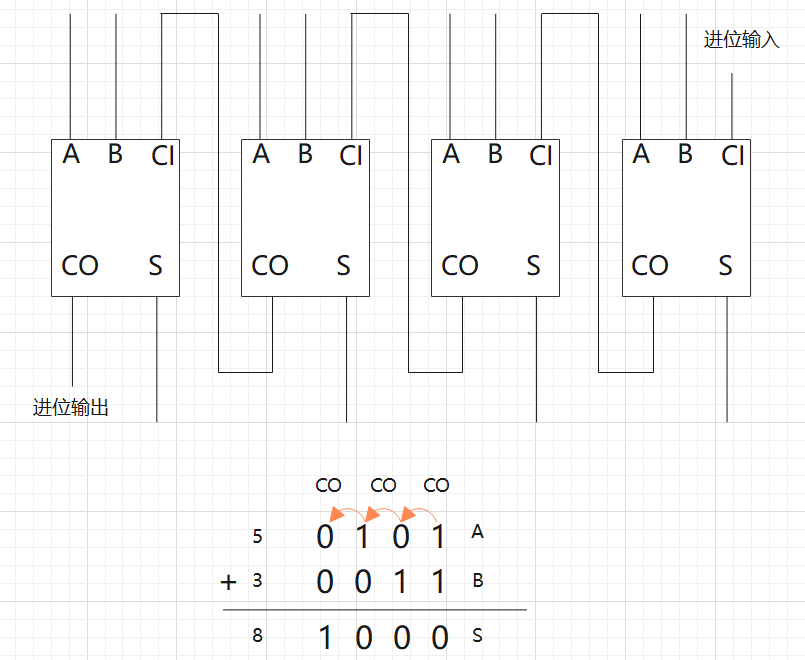
通過這組加法器的組合,我們就能計算十進制的 5+3=8 運算,很難想象,這樣的運算居然是我們通過幾個開關(guān)實現(xiàn)的!實際上這正是現(xiàn)代計算機進行加法計算的原理。
這里,你有沒驚呼:
臥槽,還有這種操作!
臥槽,這么簡單我怎么沒想到!
不過先別驚訝的太早,后面還有更讓你驚訝的。
到這里,我們已經(jīng)能夠通過我們設(shè)計的邏輯電路來計算加法了,但是還有個重要的問題:減法如何計算呢?因為計算減法涉及到借位這種繁瑣的操作,而上面我們設(shè)計的電路只能進位,難道我們還要為減法設(shè)計特定的邏輯電路嗎,答案肯定是否定的,那樣我們的電路就會非常復(fù)雜,我們考慮的是如何通過現(xiàn)有的邏輯電路,也就是如何通過加法來計算減法呢?
這個問題特別有意思,有人會說了,減去一個數(shù)等于加上這個數(shù)的負數(shù),比如 5-3=2 這個式子,可問題是這樣的說法實際上還是在計算減法,按照我們目前設(shè)計的開關(guān)電路是實現(xiàn)不了的,那怎么辦呢?
想象一下,我們上小學(xué)的時候,剛開始學(xué)習三位數(shù)的減法的時候,我們都不喜歡一些帶有借位的減法,比如
我們這里用一個技巧,先用 999 減去減數(shù) 147,顯然這個算式不會產(chǎn)生借位:
為什么這個間接的運算會正確呢?這是因為的原題目可以化成下面的運算:
到這里,你可能會有疑惑:可這個式子還用到了減法啊,而且是兩次,難道計算機在計算的時候還會有技巧跳過這個減法嗎?
在這里,神奇的事情發(fā)生了,由于計算機采用的是二進制,第一個減法也就是求補數(shù)是從一串1的數(shù)字中減去的,而二進制求補的運算不像十進制那樣,前者根本不需要做減法,而是將原來二進制中的數(shù)字1變?yōu)?, 0變?yōu)?即可(這與直接計算減法結(jié)果是一樣的,但是這個技巧對計算機來說就省下了做減法的運算),這個求相反數(shù)我們可以稱為反碼,可以通過邏輯電路中的反向器來實現(xiàn),第二個減法在二進制中減的是最高位,而這個對計算機來說我們只需要通過一個邏輯門電路來限制最高位輸出即可實現(xiàn)。
下面我們來看一下使用二進制計算這一過程有多奇妙
第一步,求補運算:

第二步,將結(jié)果加上被減數(shù) 213:

第三步,將第二步的結(jié)果加 1:
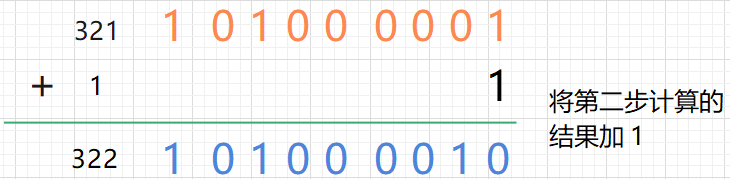
第四步,將第三步的結(jié)果最高位取反,相當于減去了256:

這樣就最終得出了我們想要的結(jié)果:66,整個過程雖然采用了兩次減法,但是在二進制看來,根本沒有使用減法。
二,為什么采用補碼來存儲整數(shù)
但是,上面這個電路還有局限性,它只能計算被減數(shù)大于減數(shù)的運算,而且不能表示負數(shù),我們想要的結(jié)果是使用現(xiàn)有的電路,讓它能夠計算加法、減法、還有負數(shù),換句話說,讓所有的運算都按照加法來實現(xiàn),該如何實現(xiàn)呢?
這時候,補碼運算就登場了。
首先,計算機為了區(qū)分整數(shù)與負數(shù),規(guī)定了符號位,規(guī)定最高位為「符號位」,0代表正數(shù),1代表負數(shù),剩下的才是「數(shù)字位」。例如對于兩個字節(jié) short 類型數(shù)字 1 在計算機內(nèi)部是這樣表示的:

而整數(shù) -1 的表示方法是這樣的,只是符號位變?yōu)榱?1:
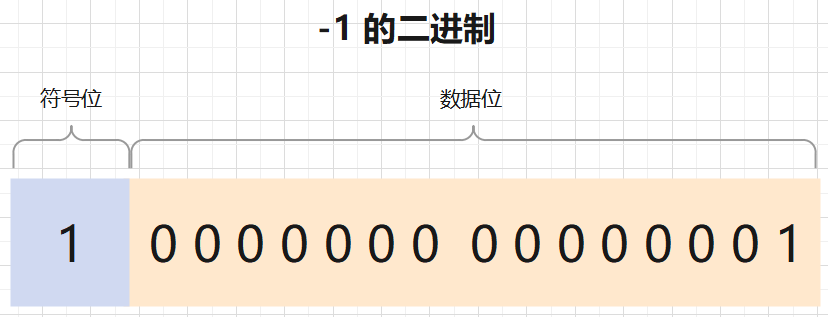
但這樣做是有代價的,意味著我們數(shù)據(jù)位的表示實際上是少了一位,導(dǎo)致我們原本能表示的數(shù)字沒那么大了。例如單字節(jié)原本能表示 0 ~ 255 之間的數(shù)字,但是因為符號位占據(jù)了 1 位,實際我們表示數(shù)據(jù)的位數(shù)變?yōu)榱?7 位,最大只能表示 127.
這時候,我們引出反碼還有補碼這個概念:正數(shù)的反碼補碼都是其原碼,而復(fù)數(shù)的反碼比較特殊,符號位不變,數(shù)據(jù)位取反就是反碼,反碼加 1 就是補碼:
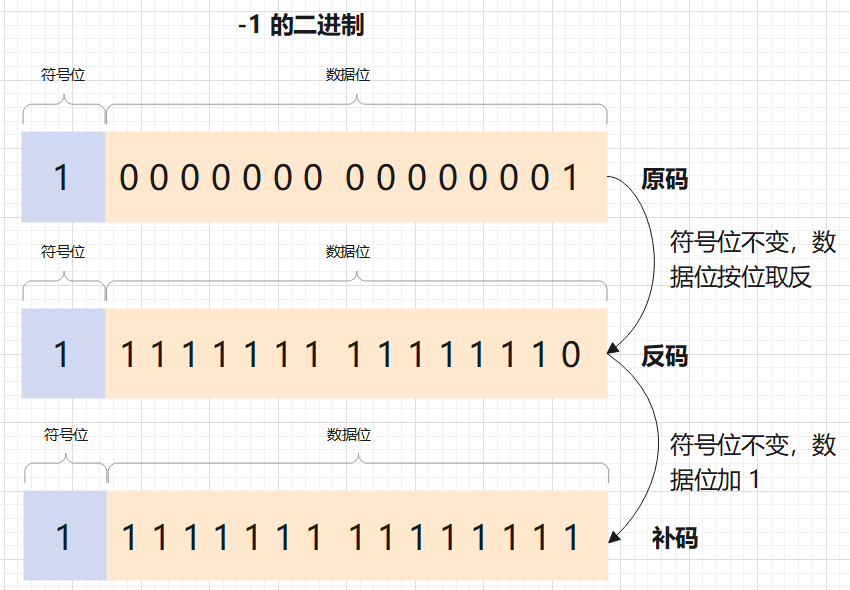
計算機內(nèi)部所有的運算都采用補碼的形式,那么為什么要這樣呢?
我們先來看如果采用原碼的形式進行計算,假設(shè)我們要計算 1 - 3,實際上就是1+(-3):

這樣得出的結(jié)果竟然是 1 + (-3) = -4,結(jié)果顯然是不正確的
那么如果我們采用反碼進行計算,會怎樣呢?

這樣得出的結(jié)果就是正確的,與我們預(yù)期的一樣,但是如果我們計算 3-1 會怎么樣呢,再試試:

最后居然得出 3+(-1)=1 的結(jié)果,這說明采用反碼運算,小數(shù)減大數(shù)沒問題,但是大數(shù)減小數(shù)結(jié)果就出了問題,直覺告訴我們,結(jié)果差了1.
隨后,人們想出了補碼這種神奇般的操作,我們看一下它的結(jié)果是怎樣的:

這樣計算的結(jié)果就與我們期待的一樣,是正確的。
再細品一下,為什么補碼運算會正確呢,我們仔細分析一下:
當大數(shù)減去小數(shù)的時候,結(jié)果一定是正數(shù)。而之前我們采用的反碼運算,結(jié)果總是少了1,如果采用補碼來計算的話,負數(shù)從反碼轉(zhuǎn)為補碼要加上1,在計算出結(jié)果后,因為正數(shù)的補碼與反碼相同,所以不用再減去,所以剛好相當于把結(jié)果加了1. 妙,不可言;
當小數(shù)減去大數(shù)的時候,結(jié)果一定是負數(shù)。如果采用補碼運算,負數(shù)從反碼轉(zhuǎn)化為補碼要加上1,而恰恰,結(jié)果是負數(shù),這個負數(shù)從補碼轉(zhuǎn)為原碼又要減去1, 剛好抵消,結(jié)果不受影響。妙,不可言。
補碼的發(fā)明,徹底簡化了我們的硬件電路,不必為減法設(shè)計額外的電路,讓我們僅僅通過加法電路就能計算減法,真是太神奇了。
看到這里,你有沒有驚呼開頭那兩句話:
臥槽,還有這種操作!
臥槽,這么簡單我怎么沒想到!
