【機(jī)器學(xué)習(xí)】線性回歸:不能忽視的三個(gè)問(wèn)題

前言

線性回歸是比較簡(jiǎn)單的機(jī)器學(xué)習(xí)算法，很多書籍介紹的第一種機(jī)器學(xué)習(xí)算法就是線性回歸算法，筆者查閱的中文書籍都是給出線性回歸的表達(dá)式，然后告訴你怎么求參數(shù)最優(yōu)化，可能部分同學(xué)會(huì)忽視一些問(wèn)題，至少筆者忽視了。因此，本文重點(diǎn)介紹了平常容易忽視的三類問(wèn)題，（1）線性回歸的理論依據(jù)是什么，（2）過(guò)擬合意味著什么。 （3）模型優(yōu)化的方向

目錄

---

1、線性回歸的理論依據(jù)是什么

2、過(guò)擬合意味著什么

3、模型優(yōu)化的方向

4、總結(jié)

線性回歸的理論依據(jù)

泰勒公式

若函數(shù) f(x)在包含x0的某個(gè)閉區(qū)間[a,b]上具有n階導(dǎo)數(shù)，且在開(kāi)區(qū)間(a,b)上具有(n+1)階 導(dǎo)數(shù) ，則對(duì) 閉區(qū)間 [a,b]上任意一點(diǎn)x，成立下式：

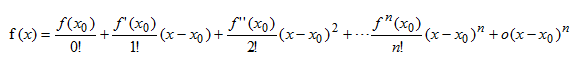
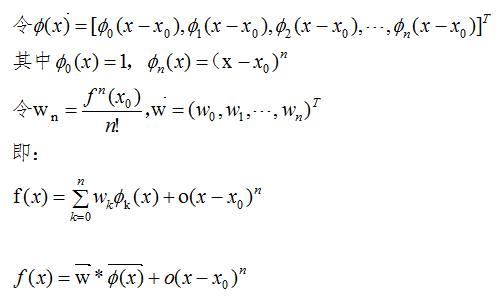
結(jié)論： 對(duì)于區(qū)間[a,b]上任意一點(diǎn)，函數(shù)值都可以用兩個(gè)向量?jī)?nèi)積的表達(dá)式近似，其中

是基函數(shù)（basis function）， 是相應(yīng)的系數(shù)。

高階表達(dá)式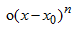表示兩者值的誤差（請(qǐng)回想您學(xué)過(guò)的線性回歸表達(dá)式）。

傅里葉級(jí)數(shù)

周期函數(shù)f(x)可以用向量?jī)?nèi)積近似， 表示基函數(shù)， 表示相應(yīng)的系數(shù)， 表示誤差。

線性回歸

由泰勒公式和傅里葉級(jí)數(shù)可知，當(dāng)基函數(shù)的數(shù)量足夠多時(shí)，向量?jī)?nèi)積無(wú)限接近于函數(shù)值。線性回歸的向量?jī)?nèi)積表達(dá)式如下：

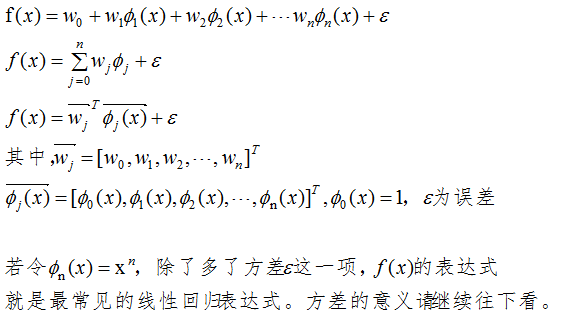
過(guò)擬合問(wèn)題

過(guò)擬合定義

構(gòu)建模型的訓(xùn)練誤差很小或?yàn)?，測(cè)試誤差很大，這一現(xiàn)象稱為過(guò)擬合。

高斯噪聲數(shù)據(jù)模型

我們采集的樣本數(shù)據(jù)其實(shí)包含了噪聲，假設(shè)該噪聲的高斯噪聲模型，均值為0，方差為。

若樣本數(shù)據(jù)的標(biāo)記為y1，理論標(biāo)記為y，噪聲為η，則有：

y1 = y +?η，（其中，η是高斯分布的抽樣）

上節(jié)的線性回歸表達(dá)式的方差 表示的意義是噪聲高斯分布的隨機(jī)抽樣，書本的線性回歸表達(dá)式把方差也包含進(jìn)去了。

過(guò)擬合原因

數(shù)學(xué)術(shù)語(yǔ)： 當(dāng)基函數(shù)的個(gè)數(shù)足夠大時(shí)，線性回歸表達(dá)式的方程恒相等。

如下圖：

機(jī)器學(xué)習(xí)術(shù)語(yǔ)：模型太過(guò)復(fù)雜以致于把無(wú)關(guān)緊要的噪聲也學(xué)進(jìn)去了。

當(dāng)線性回歸的系數(shù)向量間差異比較大時(shí)，則大概率設(shè)計(jì)的模型處于過(guò)擬合了。用數(shù)學(xué)角度去考慮，若某個(gè)系數(shù)很大，對(duì)于相差很近的x值，結(jié)果會(huì)有較大的差異，這是較明顯的過(guò)擬合現(xiàn)象。

過(guò)擬合的解決辦法是降低復(fù)雜度，后期會(huì)有相應(yīng)的公眾號(hào)文章，請(qǐng)繼續(xù)關(guān)注。

模型的優(yōu)化方向

模型的不同主要是體現(xiàn)在參數(shù)個(gè)數(shù)，參數(shù)大小以及正則化參數(shù)λ，優(yōu)化模型的方法是調(diào)節(jié)上面三個(gè)參數(shù)（但不僅限于此，如核函數(shù)），目的是找到最優(yōu)模型。

總結(jié)

本文通過(guò)泰勒公式和傅里葉級(jí)數(shù)的例子說(shuō)明線性回歸的合理性，線性回歸表達(dá)式包含了方差項(xiàng)，該方差是高斯噪聲模型的隨機(jī)采樣，若訓(xùn)練數(shù)據(jù)在線性回歸的表達(dá)式恒相等，那么就要考慮過(guò)擬合問(wèn)題了，回歸系數(shù)間差異比較大也是判斷過(guò)擬合的一種方式。模型優(yōu)化的方法有很多種，比較常見(jiàn)的方法是調(diào)節(jié)參數(shù)個(gè)數(shù)，參數(shù)大小以及正則化參數(shù)λ。

參考：

Christopher M.Bishop <<Pattern Reconition and Machine Learning>>

                      
                                          往期
                                          精彩
                                          回顧
                                        
                                      

• 適合初學(xué)者入門人工智能的路線及資料下載
• (圖文+視頻)機(jī)器學(xué)習(xí)入門系列下載
• 機(jī)器學(xué)習(xí)及深度學(xué)習(xí)筆記等資料打印
• 《統(tǒng)計(jì)學(xué)習(xí)方法》的代碼復(fù)現(xiàn)專輯
• 機(jī)器學(xué)習(xí)交流qq群955171419，加入微信群請(qǐng) 掃碼