面試官：為什么 HashMap 的加載因子是0.75？

有很多東西之前在學的時候沒怎么注意，筆者也是在重溫HashMap的時候發(fā)現(xiàn)有很多可以去細究的問題，最終是會回歸于數(shù)學的，如HashMap的加載因子為什么是0.75？

本文主要對以下內(nèi)容進行介紹：

• 為什么HashMap需要加載因子？
• 解決沖突有什么方法？
• 為什么加載因子一定是0.75？而不是0.8，0.6？

為什么HashMap需要加載因子？

HashMap的底層是哈希表，是存儲鍵值對的結(jié)構(gòu)類型，它需要通過一定的計算才可以確定數(shù)據(jù)在哈希表中的存儲位置：

static?final?int?hash(Object?key)?{
????int?h;
????return?(key?==?null)???0?:?(h?=?key.hashCode())?^?(h?>>>?16);
}
//?AbstractMap
public?int?hashCode()?{
?????int?h?=?0;
?????Iterator>?i?=?entrySet().iterator();
?????while?(i.hasNext())
?????????h?+=?i.next().hashCode();

?????return?h;
}

一般的數(shù)據(jù)結(jié)構(gòu)，不是查詢快就是插入快，HashMap就是一個插入慢、查詢快的數(shù)據(jù)結(jié)構(gòu)。

但這種數(shù)據(jù)結(jié)構(gòu)容易產(chǎn)生兩種問題：① 如果空間利用率高，那么經(jīng)過的哈希算法計算存儲位置的時候，會發(fā)現(xiàn)很多存儲位置已經(jīng)有數(shù)據(jù)了（哈希沖突）；② 如果為了避免發(fā)生哈希沖突，增大數(shù)組容量，就會導(dǎo)致空間利用率不高。

而加載因子就是表示Hash表中元素的填滿程度。

加載因子 = 填入表中的元素個數(shù) / 散列表的長度

加載因子越大，填滿的元素越多，空間利用率越高，但發(fā)生沖突的機會變大了；

加載因子越小，填滿的元素越少，沖突發(fā)生的機會減小，但空間浪費了更多了，而且還會提高擴容rehash操作的次數(shù)。

沖突的機會越大，說明需要查找的數(shù)據(jù)還需要通過另一個途徑查找，這樣查找的成本就越高。因此，必須在“沖突的機會”與“空間利用率”之間，尋找一種平衡與折衷。

所以我們也能知道，影響查找效率的因素主要有這幾種：

• 散列函數(shù)是否可以將哈希表中的數(shù)據(jù)均勻地散列？
• 怎么處理沖突？
• 哈希表的加載因子怎么選擇？

本文主要對后兩個問題進行介紹。

解決沖突有什么方法？

1. 開放定址法

Hi?=?(H(key)?+?di)?MOD?m，其中i=1,2,…,k(k<=m-1)

H(key)為哈希函數(shù)，m為哈希表表長，di為增量序列，i為已發(fā)生沖突的次數(shù)。其中，開放定址法根據(jù)步長不同可以分為3種：

1.1 線性探查法（Linear Probing）：di = 1,2,3,…,m-1

簡單地說，就是以當前沖突位置為起點，步長為1循環(huán)查找，直到找到一個空的位置，如果循環(huán)完了都占不到位置，就說明容器已經(jīng)滿了。舉個栗子，就像你在飯點去街上吃飯，挨家去看是否有位置一樣。

1.2 平方探測法（Quadratic Probing）：di = ±12, ±22，±32，…，±k2（k≤m/2）

相對于線性探查法，這就相當于的步長為di = i2來循環(huán)查找，直到找到空的位置。以上面那個例子來看，現(xiàn)在你不是挨家去看有沒有位置了，而是拿手機算去第i2家店，然后去問這家店有沒有位置。

1.3 偽隨機探測法：di = 偽隨機數(shù)序列

這個就是取隨機數(shù)來作為步長。還是用上面的例子，這次就是完全按心情去選一家店問有沒有位置了。

但開放定址法有這些缺點：

• 這種方法建立起來的哈希表，當沖突多的時候數(shù)據(jù)容易堆集在一起，這時候?qū)Σ檎也挥押茫?/section>
• 刪除結(jié)點的時候不能簡單將結(jié)點的空間置空，否則將截斷在它填入散列表之后的同義詞結(jié)點查找路徑。因此如果要刪除結(jié)點，只能在被刪結(jié)點上添加刪除標記，而不能真正刪除結(jié)點；
• 如果哈希表的空間已經(jīng)滿了，還需要建立一個溢出表，來存入多出來的元素。

2. 再哈希法

Hi?=?RHi(key),?其中i=1,2,…,k

RHi()函數(shù)是不同于H()的哈希函數(shù)，用于同義詞發(fā)生地址沖突時，計算出另一個哈希函數(shù)地址，直到不發(fā)生沖突位置。這種方法不容易產(chǎn)生堆集，但是會增加計算時間。

所以再哈希法的缺點是：增加了計算時間。

3. 建立一個公共溢出區(qū)

假設(shè)哈希函數(shù)的值域為[0, m-1]，設(shè)向量HashTable[0,…,m-1]為基本表，每個分量存放一個記錄，另外還設(shè)置了向量OverTable[0,…,v]為溢出表。基本表中存儲的是關(guān)鍵字的記錄，一旦發(fā)生沖突，不管他們哈希函數(shù)得到的哈希地址是什么，都填入溢出表。

但這個方法的缺點在于：查找沖突數(shù)據(jù)的時候，需要遍歷溢出表才能得到數(shù)據(jù)。

4. 鏈地址法（拉鏈法）

將沖突位置的元素構(gòu)造成鏈表。在添加數(shù)據(jù)的時候，如果哈希地址與哈希表上的元素沖突，就放在這個位置的鏈表上。

拉鏈法的優(yōu)點：

• 處理沖突的方式簡單，且無堆集現(xiàn)象，非同義詞絕不會發(fā)生沖突，因此平均查找長度較短；
• 由于拉鏈法中各鏈表上的結(jié)點空間是動態(tài)申請的，所以它更適合造表前無法確定表長的情況；
• 刪除結(jié)點操作易于實現(xiàn)，只要簡單地刪除鏈表上的相應(yīng)的結(jié)點即可。

拉鏈法的缺點：需要額外的存儲空間。

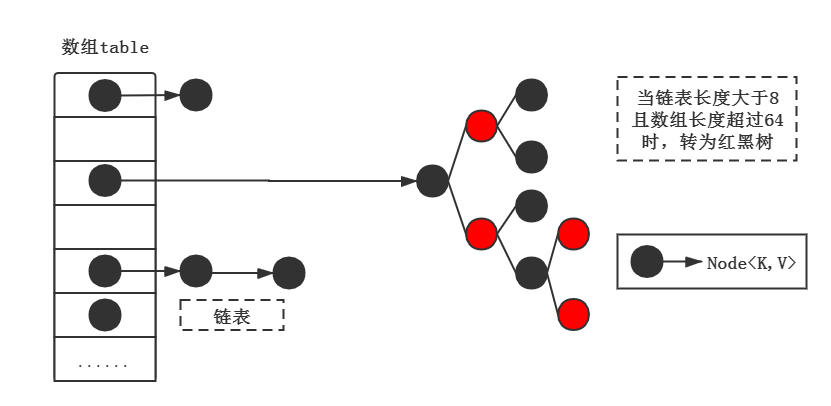
從HashMap的底層結(jié)構(gòu)中我們可以看到，HashMap采用是數(shù)組+鏈表/紅黑樹的組合來作為底層結(jié)構(gòu)，也就是開放地址法+鏈地址法的方式來實現(xiàn)HashMap。

為什么HashMap加載因子一定是0.75？而不是0.8，0.6？

從上文我們知道，HashMap的底層其實也是哈希表（散列表），而解決沖突的方式是鏈地址法。HashMap的初始容量大小默認是16，為了減少沖突發(fā)生的概率，當HashMap的數(shù)組長度到達一個臨界值的時候，就會觸發(fā)擴容，把所有元素rehash之后再放在擴容后的容器中，這是一個相當耗時的操作。

而這個臨界值就是由加載因子和當前容器的容量大小來確定的：

臨界值 = DEFAULT_INITIAL_CAPACITY * DEFAULT_LOAD_FACTOR

即默認情況下是16x0.75=12時，就會觸發(fā)擴容操作。

那么為什么選擇了0.75作為HashMap的加載因子呢？這個跟一個統(tǒng)計學里很重要的原理——泊松分布有關(guān)。

泊松分布是統(tǒng)計學和概率學常見的離散概率分布，適用于描述單位時間內(nèi)隨機事件發(fā)生的次數(shù)的概率分布。有興趣的讀者可以看看維基百科或者阮一峰老師的這篇文章：泊松分布和指數(shù)分布：10分鐘教程^[1]

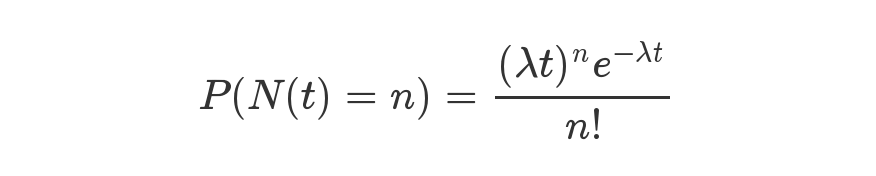
等號的左邊，P 表示概率，N表示某種函數(shù)關(guān)系，t 表示時間，n 表示數(shù)量。等號的右邊，λ 表示事件的頻率。

在HashMap的源碼中有這么一段注釋：

*?Ideally,?under?random?hashCodes,?the?frequency?of
*?nodes?in?bins?follows?a?Poisson?distribution
*?(http://en.wikipedia.org/wiki/Poisson_distribution)?with?a
*?parameter?of?about?0.5?on?average?for?the?default?resizing
*?threshold?of?0.75,?although?with?a?large?variance?because?of
*?resizing?granularity.?Ignoring?variance,?the?expected
*?occurrences?of?list?size?k?are?(exp(-0.5)?*?pow(0.5,?k)?/
*?factorial(k)).?The?first?values?are:
*?0:????0.60653066
*?1:????0.30326533
*?2:????0.07581633
*?3:????0.01263606
*?4:????0.00157952
*?5:????0.00015795
*?6:????0.00001316
*?7:????0.00000094
*?8:????0.00000006
*?more:?less?than?1?in?ten?million

在理想情況下，使用隨機哈希碼，在擴容閾值（加載因子）為0.75的情況下，節(jié)點出現(xiàn)在頻率在Hash桶（表）中遵循參數(shù)平均為0.5的泊松分布。忽略方差，即X = λt，P(λt = k)，其中λt = 0.5的情況，按公式：

計算結(jié)果如上述的列表所示，當一個bin中的鏈表長度達到8個元素的時候，概率為0.00000006，幾乎是一個不可能事件。

所以我們可以知道，其實常數(shù)0.5是作為參數(shù)代入泊松分布來計算的，而加載因子0.75是作為一個條件，當HashMap長度為length/size ≥ 0.75時就擴容，在這個條件下，沖突后的拉鏈長度和概率結(jié)果為：

0:????0.60653066
1:????0.30326533
2:????0.07581633
3:????0.01263606
4:????0.00157952
5:????0.00015795
6:????0.00001316
7:????0.00000094
8:????0.00000006

那么為什么不可以是0.8或者0.6呢？

HashMap中除了哈希算法之外，有兩個參數(shù)影響了性能：初始容量和加載因子。初始容量是哈希表在創(chuàng)建時的容量，加載因子是哈希表在其容量自動擴容之前可以達到多滿的一種度量。

在維基百科來描述加載因子：

對于開放定址法，加載因子是特別重要因素，應(yīng)嚴格限制在0.7-0.8以下。超過0.8，查表時的CPU緩存不命中（cache missing）按照指數(shù)曲線上升。因此，一些采用開放定址法的hash庫，如Java的系統(tǒng)庫限制了加載因子為0.75，超過此值將resize散列表。

在設(shè)置初始容量時應(yīng)該考慮到映射中所需的條目數(shù)及其加載因子，以便最大限度地減少擴容rehash操作次數(shù)，所以，一般在使用HashMap時建議根據(jù)預(yù)估值設(shè)置初始容量，以便減少擴容操作。

選擇0.75作為默認的加載因子，完全是時間和空間成本上尋求的一種折衷選擇。

參考資料