每日一例 | 二叉樹數(shù)據(jù)結(jié)構(gòu)了解下?

前言
數(shù)據(jù)結(jié)構(gòu)是任何編程語言的基礎(chǔ),可以這樣說,如果你熟練掌握了各種數(shù)據(jù)結(jié)構(gòu),那你就離寫出優(yōu)秀代碼不遠(yuǎn)了。為什么?因為所有的業(yè)務(wù)邏輯都是基于編程語言構(gòu)建的模型實現(xiàn)的,而模型又是基于數(shù)據(jù)結(jié)構(gòu)實現(xiàn)的,數(shù)據(jù)結(jié)構(gòu)本身是脫離于編程語言的。
之前看到一位大佬分享了他對編程的看法,他覺得一切編程都是建模,網(wǎng)上購物就是對我們傳統(tǒng)購物流程建模,社交聊天就是對我們傳統(tǒng)的交流方式建模,業(yè)務(wù)的契合程度,取決于你的建模粒度,你的建模粒度越細(xì)化,越貼合實際業(yè)務(wù),但同時也越復(fù)雜。
廢話有點多,簡單來說,其實比編程能力更重要的是建模能力,模型建的好,系統(tǒng)效率才能高。
好了,我們回到今天的內(nèi)容,今天要分享的內(nèi)容是二叉樹的實現(xiàn),以及二叉樹的常用方法實現(xiàn),算是對數(shù)據(jù)結(jié)構(gòu)的初探。我們常用的數(shù)據(jù)結(jié)構(gòu)有表、棧、隊列、樹、散列、堆等,我們常用的集合都是通過這些實現(xiàn)的,有些會復(fù)雜一點,會用到兩種數(shù)據(jù)結(jié)構(gòu)。
二叉樹
樹的基本數(shù)據(jù)結(jié)構(gòu)
最基本的樹是這樣的,它可以有多個節(jié)點:
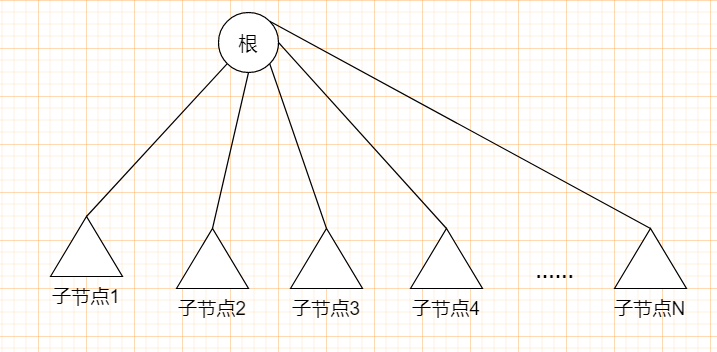
代碼實現(xiàn)是這樣的:
class TreeNode {
Object element;
TreeNode firstChild;
TreeNode nextSibling;
}
二叉樹結(jié)構(gòu)
二叉樹是最多只能有兩個子節(jié)點的樹,左邊的子節(jié)點叫left節(jié)點,右邊的子節(jié)點叫right節(jié)點:
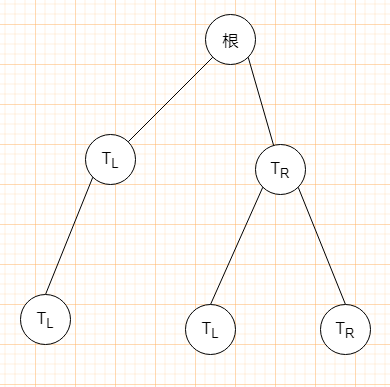
代碼實現(xiàn):
class BinaryNode<T> {
T element;
BinaryNode<T> left;
BinaryNode<T> right;
public BinaryNode() {
}
public BinaryNode(T element) {
this.element = element;
}
public BinaryNode(T element, BinaryNode<T> left, BinaryNode<T> right) {
this.element = element;
this.left = left;
this.right = right;
}
@Override
public String toString() {
return "BinaryNode{" +
"element=" + element +
", left=" + left +
", right=" + right +
'}';
}
}
二叉樹遍歷
二叉樹的遍歷方式有三種,分別叫先序遍歷、中序遍歷和后序遍歷。
先序遍歷就是從上到下,從左到右遍歷,即先打印父節(jié)點,再打印左節(jié)點,再打印右節(jié)點。
中序遍歷是有左節(jié)點先打印左節(jié)點,然后依次從左到右遍歷,左后打印右節(jié)點。
后序遍歷是先打印子節(jié)點,再打印父節(jié)點,順序也是從左到右。
以下圖為例:
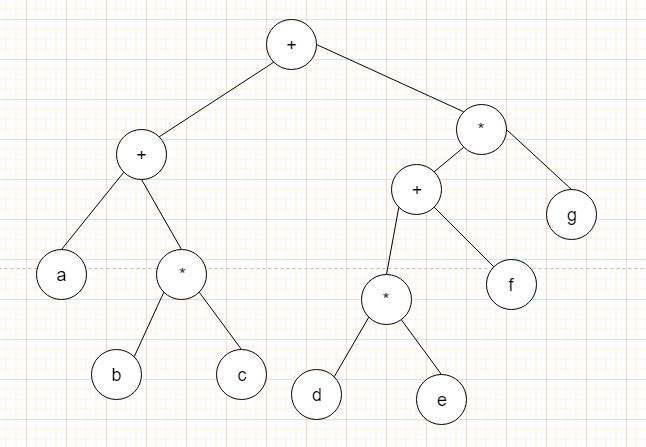
中序遍歷是這樣的:
(a + (b * C)) + (((d * e) + f) * g)
后序遍歷是這樣的:
a b c * + d e * f + g * +
先序遍歷是這樣的:
+ + a * b c * + * d e f g
這里分享下中序遍歷的實現(xiàn),這里用到了遞歸算法,其他的遍歷由于時間關(guān)系就先不寫了
private void printTree(BinaryNode<T> t) {
if (t != null) {
printTree(t.left);
System.out.println(t.element);
printTree(t.right);
}
}
總結(jié)
二叉樹是算法題中經(jīng)常要用到的一種數(shù)據(jù)結(jié)構(gòu),我還依稀記得去年有一次面試的時候,面試官讓我實現(xiàn)一個二叉樹的算法,我愣是沒寫出來,壓根就沒概念,但是一直到現(xiàn)在,對二叉樹也是知之甚少,所以從那時候我就覺得得好好補下數(shù)據(jù)結(jié)構(gòu)這塊的知識了。畢竟欠下的債,終究是要還的,像我們這些非科班出身的小伙伴,更是要好好努力呀,特別是數(shù)據(jù)結(jié)構(gòu)這一塊。沒傘的孩子,要努力奔跑呀!
每天早上的時間都很緊張,所以能分享的內(nèi)容也就不會太多,但是如果你真正去思考每天分享的知識點,應(yīng)該還是有收獲的,至少我感覺是這樣的,這種潛移默化的學(xué)習(xí)和進步,一定會讓你越來越優(yōu)秀,加油吧!
