一道頭條面試題:如何設(shè)計哈希函數(shù)并解決沖突問題

引言

本節(jié)由一道頭條面試題：如何設(shè)計哈希函數(shù)以及如何解決沖突問題展開，由以下幾個方面進行循序漸進的闡述：

• 什么是散列表？
• 什么是散列函數(shù)？
• 常見的散列函數(shù)有哪些？
• 沖突又怎么解決喃？
• 散列表的動態(tài)擴容
• 解答
• +面試題

一、散列表（哈希表、Hash 表）

不同與之前我們介紹的線性表，所有的數(shù)據(jù)都是順序存儲，當(dāng)我們需要在線性表中查找某一數(shù)據(jù)時，當(dāng)線性表過長，需要查找的數(shù)據(jù)排序比較靠后的話，就需要花費大量的時間，導(dǎo)致查找性能較差。

例如學(xué)號，如果你想通過學(xué)號去找某一名學(xué)生，假設(shè)有 n 學(xué)生，難道你要一個一個的找，這時間復(fù)雜度就為 O(n)，效率太低。當(dāng)然你也可以使用二分查找算法，那時間復(fù)雜度就為 O(logn)，有沒有更高效的解決方案喃？

我們知道數(shù)組通過下標(biāo)查找的時間復(fù)雜度為 O(1)，如果我們將學(xué)號存儲在數(shù)組里，那就簡單多了，我們可以直接通過下標(biāo)（key）找到對應(yīng)的學(xué)生。

但日常生活中，key 一般都賦予特定的含義，使用 0,1,2 ... 太過簡單了。學(xué)號通常都需要加上年級、班級等信息，學(xué)號為 010121 代表 1年級，1 班，21號。我們知道某一同學(xué)的學(xué)號就可以直接找到對應(yīng)的學(xué)生。

這就是散列！ 通過給定的學(xué)號，去訪問一種轉(zhuǎn)換算法（將學(xué)號010121轉(zhuǎn)換為1年級，1 班，21號的方法），得到對應(yīng)的學(xué)生所在地址（1年級，1 班，21號）。

其中這種轉(zhuǎn)換算法稱為散列函數(shù)（哈希函數(shù)、Hash 函數(shù)），給定的 key 稱為關(guān)鍵字，關(guān)鍵字通過散列函數(shù)計算出來的值則稱為散列值（哈希值、Hash 值）。通過散列值到?散列表（哈希表、Hash 表）中就可以獲取檢索值。

如下圖：

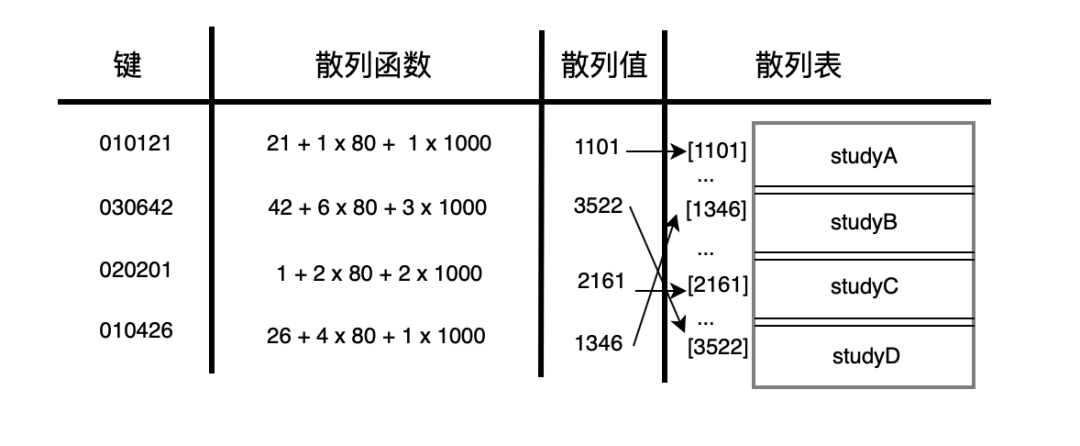
也可以說，散列函數(shù)的作用就是給定一個鍵值，然后返回值在表中的地址。

//?散列表
function?HashTable()?{
??let?table?=?[]
??this.put?=?function(key,?value)?{}
??this.get?=?function(key)?{}
??this.remove?=?function(key)?{}
}

繼續(xù)看上面學(xué)號的例子，每個學(xué)生對應(yīng)一個學(xué)號，如果學(xué)生較多，假如有 10w 個，那我們需要存儲的就有

• 10w 個學(xué)號，每個學(xué)號 6 個十進制數(shù)，一個十進制數(shù)用 4 bit 表示（1個字節(jié)=8bit）
• 散列函數(shù)
• 10w 個學(xué)生信息

這就需要多花 100000 * 6 / 2 / 1024 ?= 292.97 KB 的存儲容量用于存儲每個學(xué)生的學(xué)號，所以，散列表是一種空間換時間的存儲結(jié)構(gòu)，是在算法中提升效率的一種比較常用的方式，但是所需空間太大也會讓人頭疼，所以通常需要在二者之間權(quán)衡。

二、散列函數(shù)

這里，需要了解的是，構(gòu)造散列函數(shù)應(yīng)遵循的 原則 是：

• 散列值（value）是一個非負數(shù)：常見的學(xué)號、內(nèi)存尋址呀，都要求散列值不可能是負數(shù)
• key 值相同，通過散列函數(shù)計算出來的散列值（value）一定相同
• key 值不同，通過散列函數(shù)計算出來的散列值（value）不一定不相同

再看一個例子：學(xué)校最近要蓋一個圖書館，用于學(xué)生自習(xí)，如果給每位學(xué)生提供單獨的小桌子的話，就需要 10w 張，這顯然是不可能的，那么，有沒有辦法在得到 O(1) 的查找效率的同時、又不付出太大的空間代價呢？

散列函數(shù)就提供了這種解決方案，10w 是多，但如果我們除以 100 喃，那就 0～999，這就很好找了，也不需要那么多桌子了。

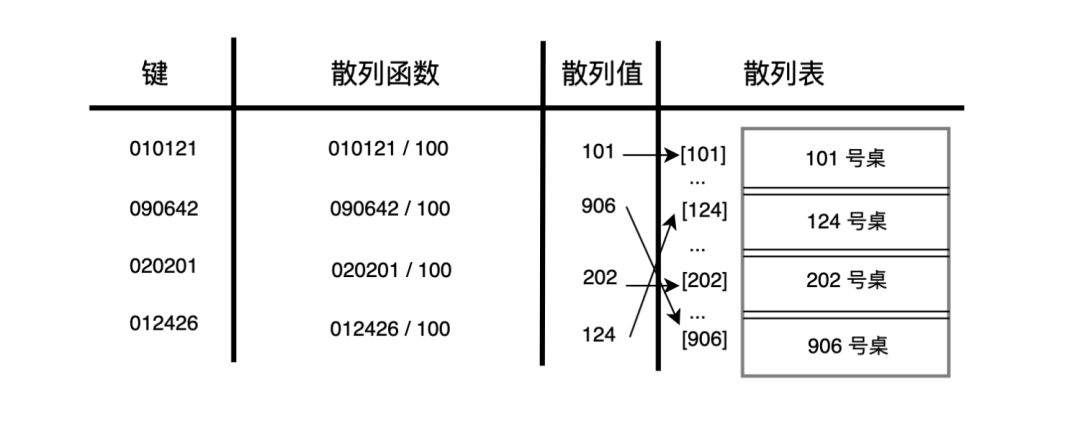
對應(yīng)的散列函數(shù)就是：

function?hashTables(key)?{
????return?Math.floor(key?/?100)
}

但在實際開發(fā)應(yīng)用中，場景不可能這么簡單，實現(xiàn)散列函數(shù)的方式也可能有很多種，例如上例，散列函數(shù)也可以是：

function?hashTables(key)?{
????return?key?>=?1000???999?:?key
}

這個實現(xiàn)的散列函數(shù)相對于上一個在 999 號桌的沖突概率就高得多，所以，選擇一個表現(xiàn)良好的散列函數(shù)就至關(guān)重要

1. 創(chuàng)建更好的散列函數(shù)

一個表現(xiàn)良好的散列函數(shù)可以大量的提高我們代碼的性能，它有更快的查找、插入、刪除等操作，更少的沖突，占用更小的存儲空間。所以構(gòu)建一個高性能的散列函數(shù)對我們至關(guān)重要。

一個好的散列函數(shù)需要具有以下基本要求：

• 易于計算：它應(yīng)該易于計算，并且不能成為算法本身。
• 統(tǒng)一分布：它應(yīng)該在哈希表中提供統(tǒng)一分布，不應(yīng)導(dǎo)致群集。
• 較少的沖突：當(dāng)元素對映射到相同的哈希值時發(fā)生沖突。應(yīng)該避免這些。

2. 常見的散列函數(shù)

• 直接尋址法：取關(guān)鍵字或關(guān)鍵字的某個線性函數(shù)值為散列地址。
• 數(shù)字分析法：通過對數(shù)據(jù)的分析，發(fā)現(xiàn)數(shù)據(jù)中沖突較少的部分，并構(gòu)造散列地址。例如同學(xué)們的學(xué)號，通常同一屆學(xué)生的學(xué)號，其中前面的部分差別不太大，所以用后面的部分來構(gòu)造散列地址。
• 平方取中法：當(dāng)無法確定關(guān)鍵字里哪幾位的分布相對比較均勻時，可以先求出關(guān)鍵字的平方值，然后按需要取平方值的中間幾位作為散列地址。這是因為：計算平方之后的中間幾位和關(guān)鍵字中的每一位都相關(guān)，所以不同的關(guān)鍵字會以較高的概率產(chǎn)生不同的散列地址。
• 取隨機數(shù)法：使用一個隨機函數(shù)，取關(guān)鍵字的隨機值作為散列地址，這種方式通常用于關(guān)鍵字長度不同的場合。
• 除留取余法：取關(guān)鍵字被某個不大于散列表的表長 n 的數(shù) m 除后所得的余數(shù) p 為散列地址。這種方式也可以在用過其他方法后再使用。該函數(shù)對 m 的選擇很重要，一般取素數(shù)或者直接用 n。

注意：無論散列函數(shù)有多健壯，都必然會發(fā)生沖突。因此，為了保持哈希表的性能，通過各種沖突解決技術(shù)來管理沖突是很重要的。

例如上例會存在一個問題，學(xué)號為 011111 與 021111 的學(xué)生，他們除以 100 后都是 111 ，這就沖突了。

三、沖突解決

在散列里，沖突是不可避免的。那怎樣解決沖突喃？

常見的解決沖突方法有幾個：

• 開放地址法（也叫開放尋址法）：實際上就是當(dāng)需要存儲值時，對Key哈希之后，發(fā)現(xiàn)這個地址已經(jīng)有值了，這時該怎么辦？不能放在這個地址，不然之前的映射會被覆蓋。這時對計算出來的地址進行一個探測再哈希，比如往后移動一個地址，如果沒人占用，就用這個地址。如果超過最大長度，則可以對總長度取余。這里移動的地址是產(chǎn)生沖突時的增列序量。
• 鏈地址法：鏈地址法其實就是對Key通過哈希之后落在同一個地址上的值，做一個鏈表。其實在很多高級語言的實現(xiàn)當(dāng)中，也是使用這種方式處理沖突的，我們會在后面著重學(xué)習(xí)這種方式。
• 再哈希法：在產(chǎn)生沖突之后，使用關(guān)鍵字的其他部分繼續(xù)計算地址，如果還是有沖突，則繼續(xù)使用其他部分再計算地址。這種方式的缺點是時間增加了。
• 建立一個公共溢出區(qū)：這種方式是建立一個公共溢出區(qū)，當(dāng)?shù)刂反嬖跊_突時，把新的地址放在公共溢出區(qū)里。

我們這里介紹兩個最簡單的：開放尋址法里的線性探測，以及鏈地址法。

1. 線性探測

線性探測是開放尋址里最簡單的方法，當(dāng)往散列表中增加一個新的元素值時，如果索引為 index 的位置已經(jīng)被占用了，那么就嘗試 index + 1 的位置，如果 index + 1 的位置也被占用了，那就嘗試 index + 2 的位置，以此類推，如果嘗試到表尾也沒找到空閑位置，則從表頭開始，繼續(xù)嘗試，直到放入散列表中。

如下圖：

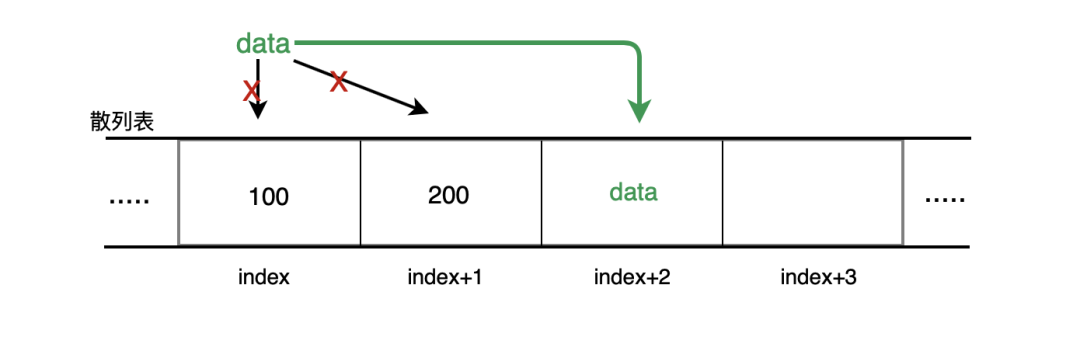
如果是刪除喃：首先排查由散列函數(shù)計算得出的散列值，與要查找的散列值對比，相同則刪除元素，如果該節(jié)點為空了，則設(shè)為 undefined ，不相等則繼續(xù)比較 index + 1 ，以此類推，直到相等或遍歷完整個散列表。

如果是查找喃：首先排查由散列函數(shù)計算得出的散列值，與要查找的散列值對比是否相等，相等則查找完成，不相等繼續(xù)排查 index + 1 ，直到遇到空閑節(jié)點（ undefined 節(jié)點忽略不計），則返回查找失敗，散列表中沒有查找值。

很簡單，但它也有自己的局限性，當(dāng)散列表中元素越來越多時，沖突的幾率就越來越大。

最壞情況下的時間復(fù)雜度為 O(n)。

2. 鏈地址法

鏈地址也很簡單，它給每一個散列表中的節(jié)點建立一個鏈表，關(guān)鍵字 key 通過散列函數(shù)轉(zhuǎn)換為散列值，找到散列表中對應(yīng)的節(jié)點時，放入對應(yīng)鏈表中即可。

如下圖：

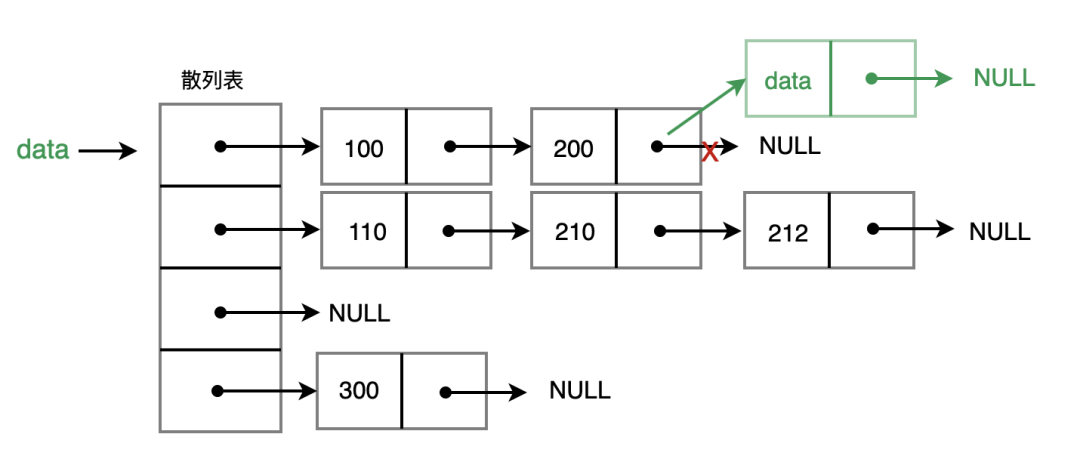
插入：像對應(yīng)的鏈表中插入一條數(shù)據(jù)，時間復(fù)雜度為 O(1)

查找或刪除：從鏈頭開始，查找、刪除的時間復(fù)雜度為 O(k)，k為鏈表的長度

四、動態(tài)擴容

前面在介紹數(shù)組的時候，我們已經(jīng)介紹過擴容，在 JavaScript 中，當(dāng)數(shù)組 push 一個數(shù)據(jù)時，如果數(shù)組容量不足，則 JavaScript 會動態(tài)擴容，新容量為老的容量的 1.5 倍加上 16。

在散列表中，隨著散列值不斷的加入散列表中，散列表中數(shù)據(jù)越來越慢，沖突的幾率越來越大，查找、插入、刪除等操作的時間復(fù)雜度越來越高，散列表也需要不斷的動態(tài)擴容。

五、回答開頭問題

如何設(shè)計哈希函數(shù)以及如何解決沖突，這是哈希表考察的重要問題。

如何設(shè)計哈希函數(shù)？

一個好的散列函數(shù)需要具有以下基本要求：

• 易于計算：它應(yīng)該易于計算，并且不能成為算法本身。
• 統(tǒng)一分布：它應(yīng)該在哈希表中提供統(tǒng)一分布，不應(yīng)導(dǎo)致群集。
• 較少的沖突：當(dāng)元素對映射到相同的哈希值時發(fā)生沖突。應(yīng)該避免這些。

如何解決沖突？

常見的解決沖突方法有幾個：

• 開放地址法（也叫開放尋址法）：實際上就是當(dāng)需要存儲值時，對Key哈希之后，發(fā)現(xiàn)這個地址已經(jīng)有值了，這時該怎么辦？不能放在這個地址，不然之前的映射會被覆蓋。這時對計算出來的地址進行一個探測再哈希，比如往后移動一個地址，如果沒人占用，就用這個地址。如果超過最大長度，則可以對總長度取余。這里移動的地址是產(chǎn)生沖突時的增列序量。
• 鏈地址法：鏈地址法其實就是對Key通過哈希之后落在同一個地址上的值，做一個鏈表。其實在很多高級語言的實現(xiàn)當(dāng)中，也是使用這種方式處理沖突的，我們會在后面著重學(xué)習(xí)這種方式。
• 再哈希法：在產(chǎn)生沖突之后，使用關(guān)鍵字的其他部分繼續(xù)計算地址，如果還是有沖突，則繼續(xù)使用其他部分再計算地址。這種方式的缺點是時間增加了。
• 建立一個公共溢出區(qū)：這種方式是建立一個公共溢出區(qū)，當(dāng)?shù)刂反嬖跊_突時，把新的地址放在公共溢出區(qū)里。

六、常見的哈希表問題

我們已經(jīng)刷過的（https://github.com/sisterAn/JavaScript-Algorithms）：

• 騰訊&leetcode349：給定兩個數(shù)組，編寫一個函數(shù)來計算它們的交集
• 字節(jié)&leetcode1：兩數(shù)之和
• 騰訊&leetcode15：三數(shù)之和

今天刷一道 leetcode380：常數(shù)時間插入、刪除和獲取隨機元素

leetcode380：常數(shù)時間插入、刪除和獲取隨機元素

設(shè)計一個支持在平均?時間復(fù)雜度 O(1)?下，執(zhí)行以下操作的數(shù)據(jù)結(jié)構(gòu)。

• insert(val) ：當(dāng)元素 val 不存在時，向集合中插入該項。
• remove(val) ：元素 val 存在時，從集合中移除該項。
• getRandom ：隨機返回現(xiàn)有集合中的一項。每個元素應(yīng)該有 相同的概率 被返回。

示例 :

//?初始化一個空的集合。
RandomizedSet?randomSet?=?new?RandomizedSet();

//?向集合中插入 1 。返回 true 表示 1 被成功地插入。
randomSet.insert(1);

//?返回 false ，表示集合中不存在 2 。
randomSet.remove(2);

//?向集合中插入 2 。返回 true 。集合現(xiàn)在包含?[1,2]?。
randomSet.insert(2);

// getRandom 應(yīng)隨機返回 1 或 2 。
randomSet.getRandom();

//?從集合中移除 1 ，返回 true 。集合現(xiàn)在包含?[2]?。
randomSet.remove(1);

// 2 已在集合中，所以返回 false 。
randomSet.insert(2);

//?由于 2 是集合中唯一的數(shù)字，getRandom 總是返回 2 。
randomSet.getRandom();

歡迎將解答提到 https://github.com/sisterAn/JavaScript-Algorithms/issues/48 ，這里我們提交了前端所用到的算法系列文章以及題目（已解答），歡迎star，如果感覺不錯，點個在看支持一下唄?

瓶子君將明日解答?

閱讀??

歡迎關(guān)注「前端瓶子君」，回復(fù)「交流」加入前端交流群！

歡迎關(guān)注「前端瓶子君」，回復(fù)「算法」自動加入，從0到1構(gòu)建完整的數(shù)據(jù)結(jié)構(gòu)與算法體系！

在這里，瓶子君不僅介紹算法，還將算法與前端各個領(lǐng)域進行結(jié)合，包括瀏覽器、HTTP、V8、React、Vue源碼等。

在這里，你可以每天學(xué)習(xí)一道大廠算法題（阿里、騰訊、百度、字節(jié)等等）或 leetcode，瓶子君都會在第二天解答喲！

“在看轉(zhuǎn)發(fā)”是最大的支持