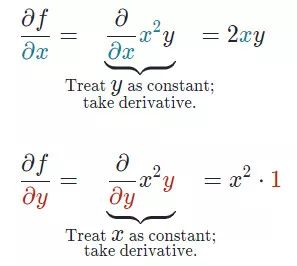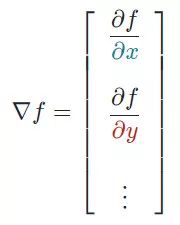點擊上方“小白學視覺”,選擇加"星標"或“置頂”
重磅干貨,第一時間送達
來源:AI科技評論
對于諸位“MLer”而言,梯度下降這個概念一定不陌生,然而從直觀上來看,梯度下降的復雜性無疑也會讓人“敬而遠之”。本文作者 Suraj Bansal 通過對梯度下降背后的數(shù)學原理進行拆解,并配之以簡單的現(xiàn)實案例,以輕松而有趣的口吻帶大家深入了解梯度下降這一在機器學習領域至關重要的方法。
“敏捷軟件開發(fā)”定義了迭代產(chǎn)品開發(fā)的過程,以下步驟可通過這一過程執(zhí)行。市場調(diào)研后進行產(chǎn)品構建
產(chǎn)品商業(yè)化并進入市場
評估消費者滿意度和市場滲透率
對反饋及時回應,并更新迭代產(chǎn)品
重復上述過程
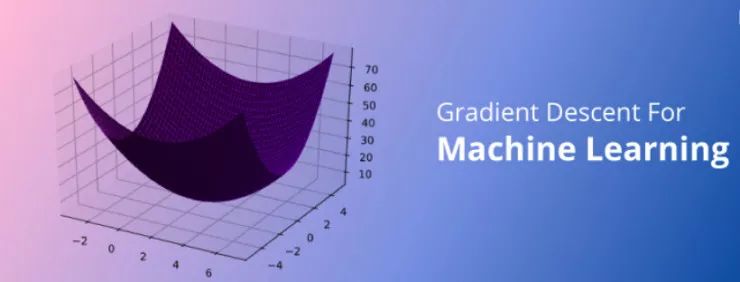
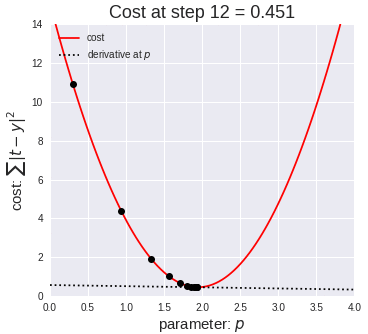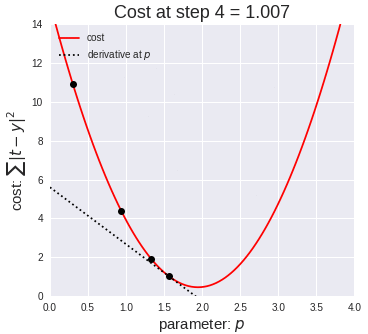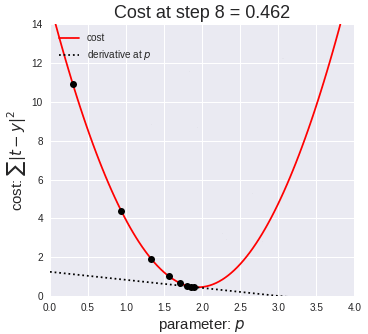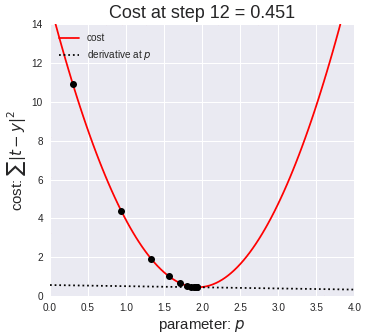
這個過程實質(zhì)上是將市場測試、 收集反饋和產(chǎn)品迭代反復進行,直到能以最小的誤差實現(xiàn)最大的市場滲透率。此循環(huán)重復多次,并確保消費者可以在每個步驟中提供一定的反饋來影響產(chǎn)品的更改策略。實際上,這種看似簡單的反復迭代過程很好地體現(xiàn)在梯度下降原理中。梯度下降能夠通過首先計算出成本函數(shù)的梯度、然后更新梯度對應的現(xiàn)有參數(shù)從而最小化成本函數(shù)來處理。梯度將具有眾多變量的函數(shù)轉換為一個向量(稍后我們將對該話題進行討論)。了解梯度下降背后的多元演算聽起來可能會讓人十分畏懼……別怕,下面我將對梯度下降背后的原理做出解釋并且僅跟大家探討理解梯度下降所需的數(shù)學概念。
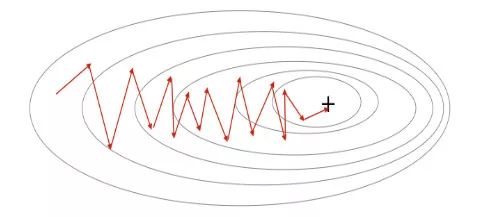
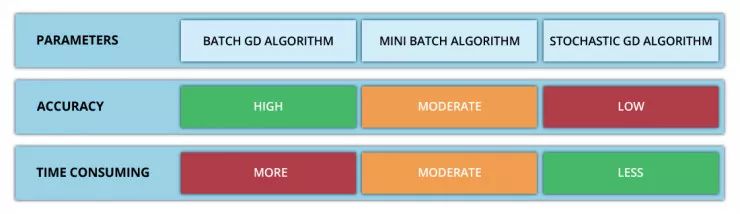
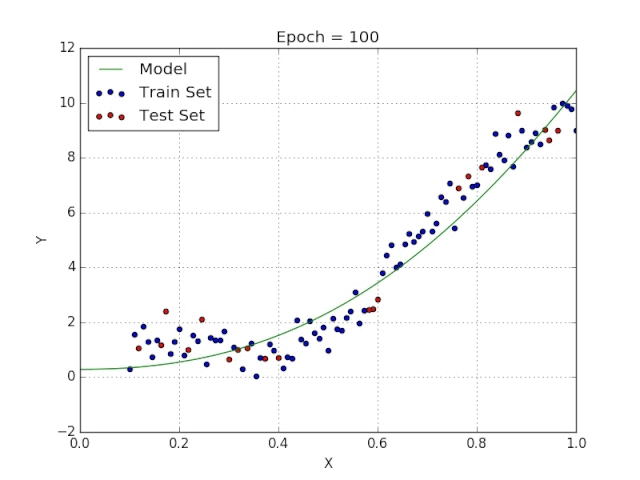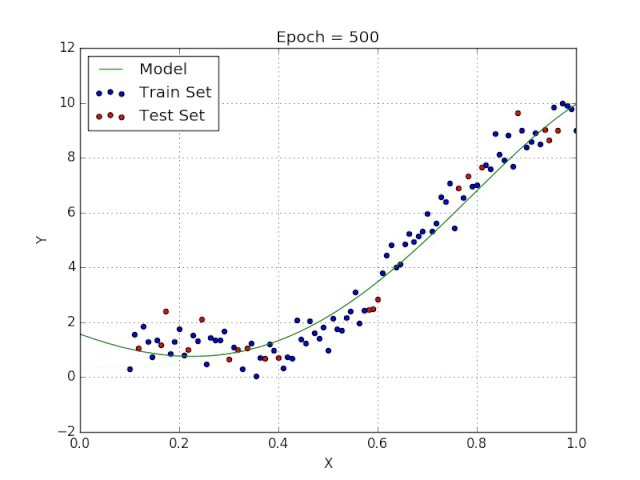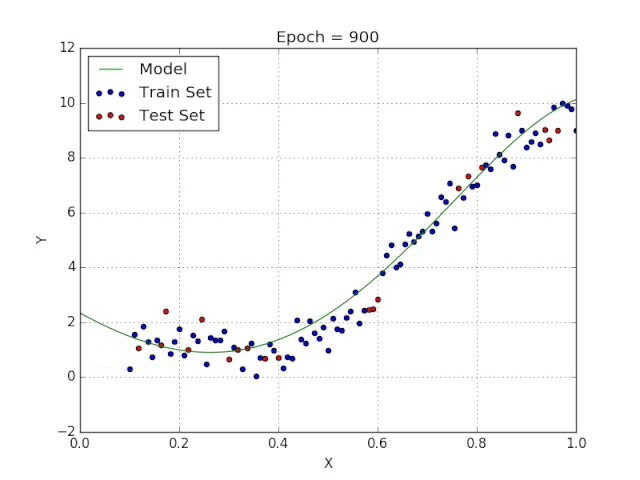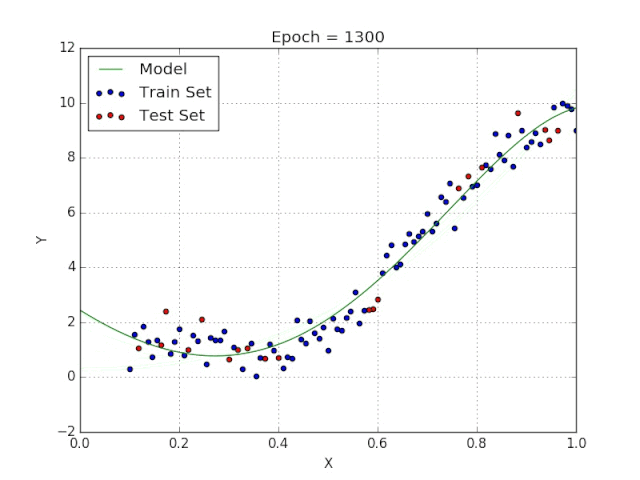
梯度下降采用機器學習算法實現(xiàn)了三種主要的變體,每個變體在計算效率上各異并且都具有各自獨特的優(yōu)勢。批量梯度下降(Batch Gradient Descent)可以說是梯度下降變體中最簡單的一種。這整個過程可以看作是訓練迭代的次數(shù)(Epoch),即以決定訓練用來更新模型權重的向量的次數(shù)。批量梯度下降的誤差通過訓練集每一批單獨的樣本計算出來,并且在所有訓練點數(shù)都在一個 Epoch 內(nèi)經(jīng)過機器學習算法的訓練后更新模型參數(shù)。該方法的誤差梯度和收斂速度較為穩(wěn)定,可以實現(xiàn)足夠水平的計算效率。但是,由于該模型僅在分析了整個訓練集之后才對權重進行迭代,此時的收斂狀態(tài)可能不是最優(yōu)的狀態(tài),事實上,該模型還可以優(yōu)化以達到更精確的結果!下面進入……隨機梯度下降!這兩種方法之間的根本區(qū)別在于,隨機梯度下降法隨機化了整個數(shù)據(jù)集并對每個單獨的訓練樣本進行權重和參數(shù)的更新,而批量梯度下降是在分析了整個訓練集之后對參數(shù)進行更新。對模型連續(xù)更新可以提供更高的準確率和更快的計算速度。但是,頻繁的更改會產(chǎn)生更多的梯度噪聲,這意味著它會在誤差最小值區(qū)域(成本函數(shù)最低的點)內(nèi)來回振蕩。因此,每次運行測試都會存在一些差異。好的,這兩種方法都有一些明顯的優(yōu)缺點,那么到底哪種方法更適合你的機器學習模型?這也不是什么很難的問題——都不是!再接下來進入……迷你批次梯度下降!它基本上結合了批量梯度下降的效率和隨機梯度下降的整體魯棒性。該方法通過將數(shù)據(jù)集聚類為更小的批量(通常在30–500個訓練點數(shù)之間),并且模型對每個單獨批量執(zhí)行迭代。它通過使用高度優(yōu)化的矩陣來提高效率和準確性,這有效減小了參數(shù)更新的方差。所有梯度下降變體都將使用以下公式進行建模。每當模型進行反向傳播后,都會執(zhí)行此迭代,直到成本函數(shù)達到其收斂點為止。權重向量存在于 x-y 平面中,將對應每個權重的損失函數(shù)的梯度與學習率相乘,然后用向量減去二者的乘積。
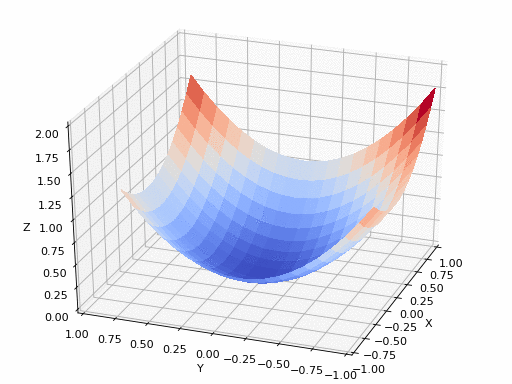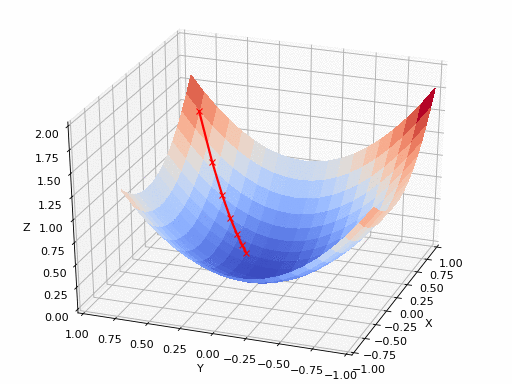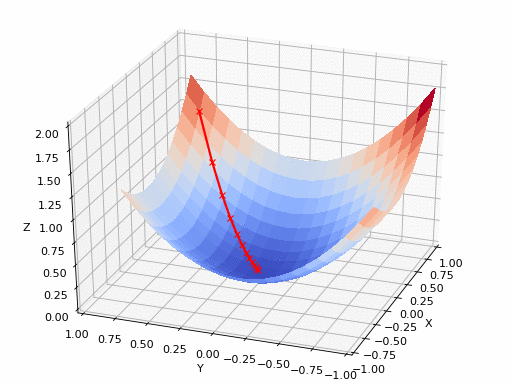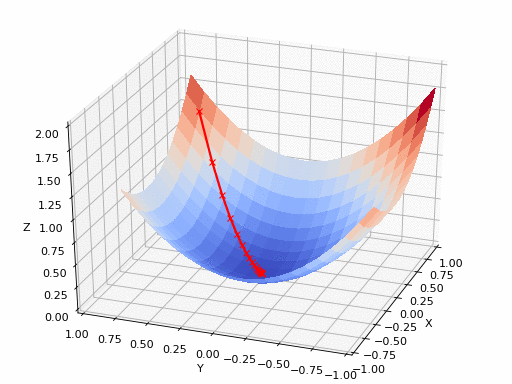
偏導數(shù)是用于更新參數(shù) θ0、θ1和alpha(學習率)的梯度,而alpha是需要用戶自己給定的非常重要的超參數(shù)。M 代表更新的次數(shù),i 代表梯度更新的起始點。我們知道一個多變量函數(shù)的偏導數(shù),就是它關于其中一個變量的導數(shù)而保持其他變量恒定。但是該函數(shù)的整個求導過程是怎樣的呢?首先,讓我們了解偏導數(shù)背后的數(shù)學原理。計算像 f(x,y)=x2* y 這樣的多變量函數(shù)的過程可以分解如下:好吧,我知道你此時在想什么——導數(shù)本身已經(jīng)很復雜很枯燥,為什么還使用偏導數(shù)而不完全使用導數(shù)!函數(shù)輸入由多個變量組成,因此,其中涉及的概念就是多變量演算。偏導數(shù)用于評估每個變量相對于其他變量作為常量時的變化情況。梯度實質(zhì)上輸出的是標量值多變量函數(shù)多維輸入的一維值。梯度表示圖形切線的斜率,該斜率指向函數(shù)最大增長率的方向。這個導數(shù)代表了成本函數(shù)的趨勢或斜率值。本質(zhì)上,任何給定函數(shù) f 的梯度(通常用?f表示)可以解釋為一個向量所有偏導數(shù)的集合。想象自己站在函數(shù) f 以一定間隔排列的點(x0,y0…)之中。向量?f(x0,y0…)將識別出使 f函數(shù)值增加的最快行進方向。有趣的是,梯度矢量?f(x0,yo…)也垂直于函數(shù) f 的輪廓線!
假設偏導數(shù)是具有 n 個偏導數(shù)的 n 次導數(shù),這些偏導數(shù)可以將每個單獨的變量與其他看作常數(shù)的變量隔離開來。而梯度將每個偏導數(shù)組合成一個向量。
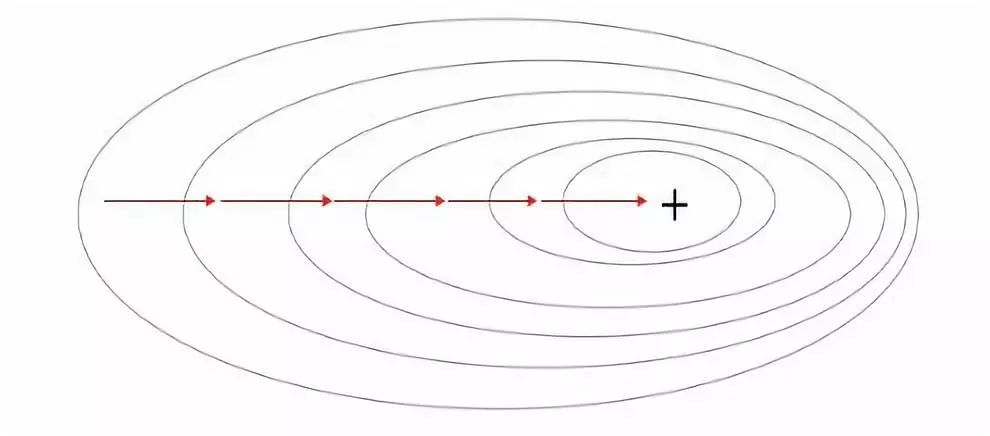
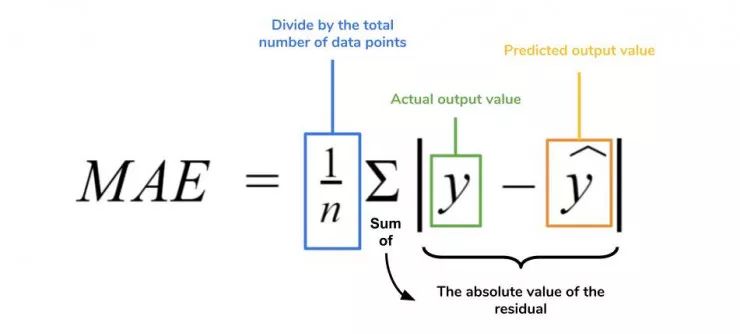
梯度可以確定移動的方向。學習率將決定我們采取步長的大小。學習率本質(zhì)上是一個超參數(shù),它定義了神經(jīng)網(wǎng)絡中權重相對于損失梯度下降的調(diào)整幅度。這個參數(shù)決定了我們朝著最佳權重移動的速度的快慢,同時將每個步長的成本函數(shù)最小化。高學習率可以在每一步中覆蓋更多的區(qū)域,但是可能會跳過成本函數(shù)的最小值;低學習率則需要花上很久的時間才能到達成本函數(shù)的最小值。下面我以我的小外甥和他對狗的喜愛為例,來對這兩種情況進行說明:我們假設 Arnav 美夢成真:看到了25只漂亮的拉布拉多犬,并且它們都是黑色的。那自然而然地,Arnav 就會識別出這種一致的黑色,并將這種黑色關聯(lián)為他之后在辨認狗這種動物時要尋找的主要特征。假設我突然給他看一條白色的狗,然后告訴他這是一只狗,如果學習率低,他會繼續(xù)認為所有的狗都一定具備黑色的特征,而這條白色的狗就是一條異常的狗。如果學習率高,Arnav 就會轉而相信所有的狗都應該是白色的,并且任何跟他的新預想不一致的情況都會被視為錯誤,即便之前他看到過 25只黑色狗。在理想的學習率下,Arnav 將意識到顏色不是對狗進行分類的主要屬性,他將繼續(xù)去發(fā)現(xiàn)狗的其他特征。理想的學習速率無疑是最好的,因為它能夠在準確性和時間成本之間找到一個平衡點。成本函數(shù)可以衡量模型的性能,在神經(jīng)網(wǎng)絡訓練過程中,我們要確保將成本函數(shù)一直減小,直到達到最小值。成本函數(shù)實質(zhì)上是通過回歸指標,例如平均絕對誤差和均方誤差,來量化預測值和期望值之間的總誤差。平均絕對誤差測量的是一組預測樣本中平均誤差的大小,而無需評估其方向或矢量,可以通過以下公式進行建模。均方誤差可找到預測值與實際值之間平均差的平方。除了最后取值為平方而不是絕對值這一點以外,均方誤差與平均絕對誤差 MAE 的原理基本一致。其對于部分誤差值的度量標準不再是坐標系內(nèi)點之間的距離,而是找到由測量點之間的距離產(chǎn)生的形狀(通常為正方形)區(qū)域。讓我們看這樣一個類比,以進一步了解梯度下降的直觀原理!想象一下,你站在珠穆朗瑪峰峰頂上,現(xiàn)在要完成通往山底的任務,這聽起來相當簡單且直觀對吧?然而,(現(xiàn)在有一個你需要考慮的細節(jié)信息是——你完全是一個盲人)這里出現(xiàn)了一則你需要重新考慮的小信息——你是盲人。這無疑使得任務變得更加艱巨,但目標也并非完全不可能實現(xiàn)。在你開始朝著更大傾斜度的方向移動前,你需要邁出一小步一小步。在你抵達山底之前,此方法需要進行無數(shù)次迭代以最終達到目的地。這從本質(zhì)上模仿了梯度下降的理念,在梯度下降中,模型通過后向傳播以最終到達山的最低點。山脈類似于在空間中繪制的數(shù)據(jù)圖,行走的步長類似于學習率,感受地形陡峭程度就類似于算法計算數(shù)據(jù)集參數(shù)的梯度。若假設正確,選擇的方向會降低成本函數(shù)。山的底部代表了機器的權重的最佳值(成本函數(shù)已經(jīng)被最小化)。對于那些不熟悉的變量,在所有統(tǒng)計模型學科中常常使用回歸分析來研究多變量函數(shù)之間的關系以進行預測分析。代表期望值和實驗值之間誤差的線稱為回歸線,每個殘差值都可以通過與其方差與最佳擬合線連接的垂直線段描繪出來。
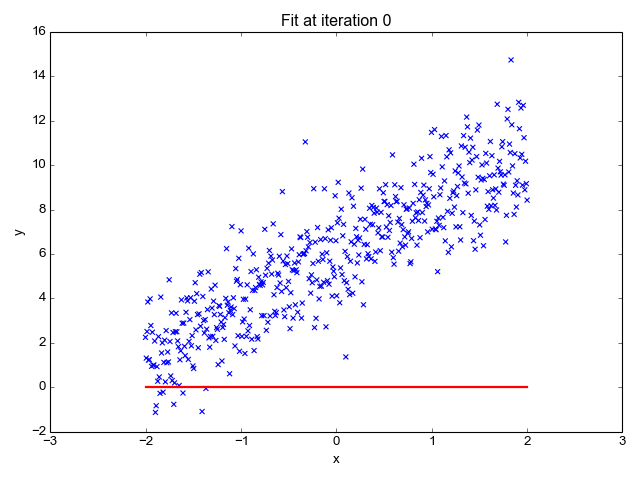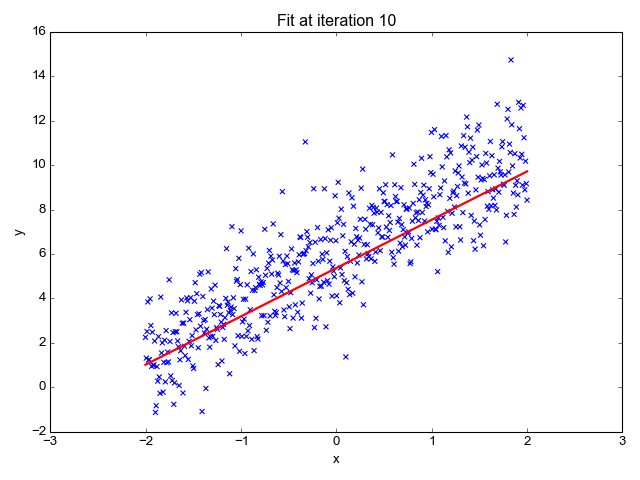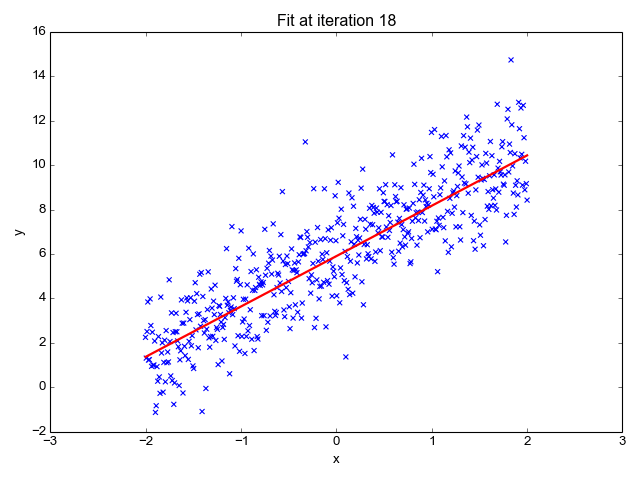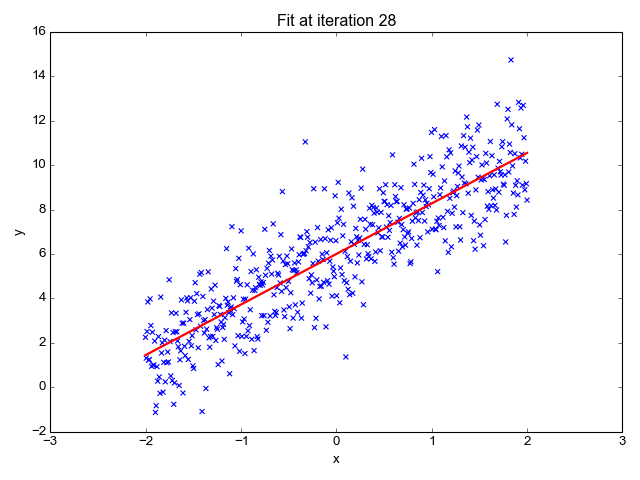
下面的公式將 x 表示為輸入的訓練數(shù)據(jù)(參數(shù)為單變量或單輸入變量),假設進行了監(jiān)督學習,則 y 表示數(shù)據(jù)的標簽。
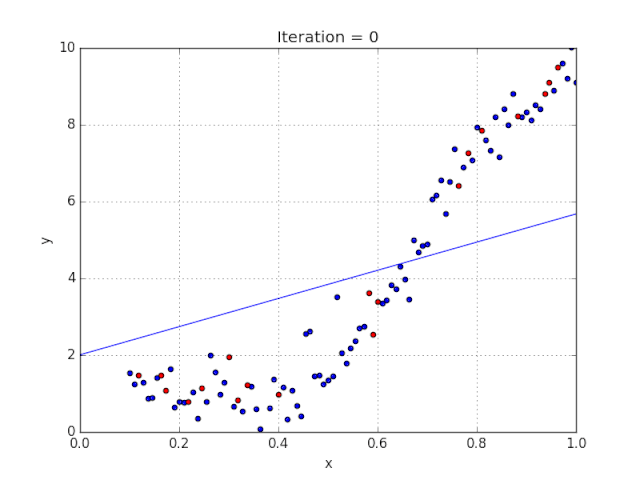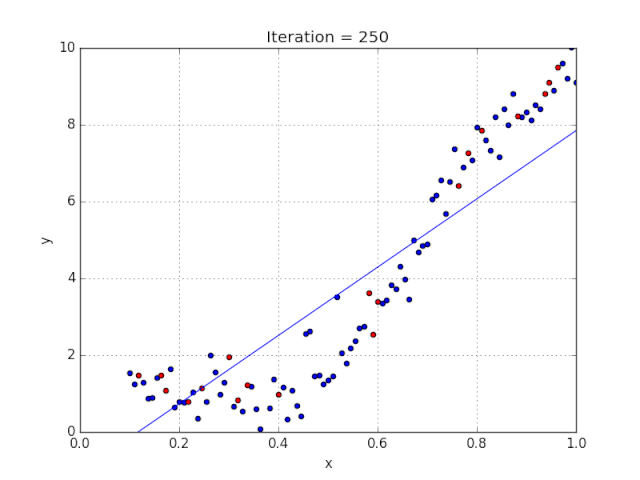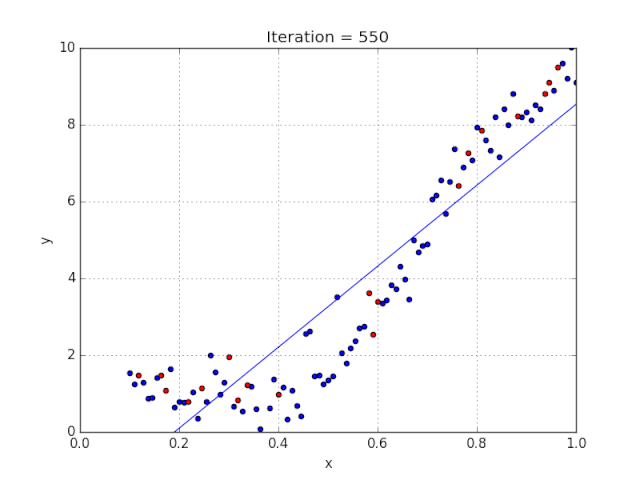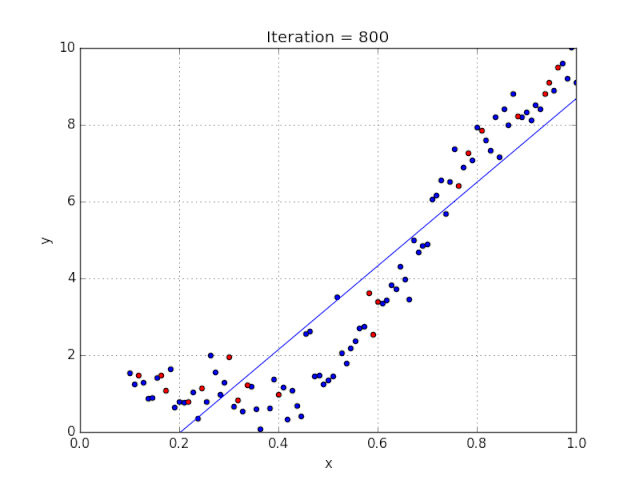
Elon 在 salesx 擔任兼職市場總監(jiān),他收集了過去一年的促銷工作促銷活動的付款額與銷售額的數(shù)據(jù),給未來銷售和促銷提供一些指導性建議。Elon認為該數(shù)據(jù)應該是線性的,所以用散點圖的方式來呈現(xiàn)這些信息,橫縱坐標分別為新客戶數(shù)量和花費的成本。Elon構造了回歸線,其目的是為了更好地理解和預測salesx將通過新的營銷理念獲得多少客戶。線性回歸可以很好地顯示數(shù)據(jù)集中兩個相關變量中存在的結構和趨勢。但是,考慮到線性函數(shù)的行為,而由于在非線性關系中依然可以清楚地表現(xiàn)出一定的相關性,它們無法將非線性的回歸關系進行準確反映。多項式回歸能夠?qū)?n 次方函數(shù)之間的關系進行建模,并且可以以低于線性回歸的誤差函數(shù)值擬合某些數(shù)據(jù)集。盡管多項式回歸可以更好地擬合函數(shù)的曲率,并且可以最準確地表示兩個變量之間的關系,但它們對異常值極為敏感,那些異常值很容易造成數(shù)據(jù)偏離。本文來源:
https://medium.com/datadriveninvestor/the-math-and-intuition-behind-gradient-descent-13c45f367a11
下載1:OpenCV-Contrib擴展模塊中文版教程
在「小白學視覺」公眾號后臺回復:擴展模塊中文教程,即可下載全網(wǎng)第一份OpenCV擴展模塊教程中文版,涵蓋擴展模塊安裝、SFM算法、立體視覺、目標跟蹤、生物視覺、超分辨率處理等二十多章內(nèi)容。下載2:Python視覺實戰(zhàn)項目52講在「小白學視覺」公眾號后臺回復:Python視覺實戰(zhàn)項目,即可下載包括圖像分割、口罩檢測、車道線檢測、車輛計數(shù)、添加眼線、車牌識別、字符識別、情緒檢測、文本內(nèi)容提取、面部識別等31個視覺實戰(zhàn)項目,助力快速學校計算機視覺。在「小白學視覺」公眾號后臺回復:OpenCV實戰(zhàn)項目20講,即可下載含有20個基于OpenCV實現(xiàn)20個實戰(zhàn)項目,實現(xiàn)OpenCV學習進階。交流群
歡迎加入公眾號讀者群一起和同行交流,目前有SLAM、三維視覺、傳感器、自動駕駛、計算攝影、檢測、分割、識別、醫(yī)學影像、GAN、算法競賽等微信群(以后會逐漸細分),請掃描下面微信號加群,備注:”昵稱+學校/公司+研究方向“,例如:”張三?+?上海交大?+?視覺SLAM“。請按照格式備注,否則不予通過。添加成功后會根據(jù)研究方向邀請進入相關微信群。請勿在群內(nèi)發(fā)送廣告,否則會請出群,謝謝理解~