算法原理：大數(shù)據(jù)處理的分治思想！

引言

MapReduce（分治算法的應用） 是 Google 大數(shù)據(jù)處理的三駕馬車之一，另外兩個是 GFS 和 Bigtable。它在倒排索引、PageRank 計算、網(wǎng)頁分析等搜索引擎相關的技術(shù)中都有大量的應用。

盡管開發(fā)一個MapReduce看起來很高深，感覺遙不可及。實際上，萬變不離其宗，它的本質(zhì)就是分治算法思想，分治算法。如何理解分治算法？為什么說 MapRedue 的本質(zhì)就是分治算法呢？

分治是一種被廣泛應用的有效方法，它的基本思想是把最初的問題分解成若干子問題，然后，在逐個解決各個子問題的基礎上得到原始問題的解。所謂分治就是“分而治之”的意思。由于分解出的每個子問題總是要比最初的問題容易些，因而分治策略往往能夠降低原始問題的難度，或者提高解決問題的效率。例如，到圖書館查找某一本書，一般都是根據(jù)大的類別確定書應該在文學類、自然科學類，還是在外語類，直奔相應的樓層，再按照下一級的分類找到對應的藏書室，如有必要，再按更細的分類找到對應的書架，最終找到需要的書。又如，學校要評選出本年度的三好學生，便把任務分配到各個學院，學院接到任務再分配到年級、班級，班級、年級評選的結(jié)果在學院匯總后上報學校，學校再把各學院報來的名單綜合起來，從而完成整個評選工作。

根據(jù)如何由分解出的子問題求出原始問題的解，分治策略又可分為兩種情形：其一是原始問題的解只存在于分解出的某一個子問題中，則只需要在原始問題的一個劃分中求解即可，如前面的第一個例子；另一種情形則是原始問題的解需要由各個子問題的解再經(jīng)過綜合處理而得到，第二個例子就是這種類型。無論是哪一種情況，適當運用分治策略往往可以較快地縮小問題求解的范圍，從而加快問題求解的速度。

分治策略運用于計算機算法時，往往會出現(xiàn)分解出來的子問題與原始問題類型相同的現(xiàn)象，而與原問題相比，各個子問題的“尺寸”變小了。這剛好符合“遞歸”的特征，因此計算機中的分治策略往往是與遞歸聯(lián)系在一起的。

全文如下：

本文從分治算法的思想出發(fā)，深度講解該算法的使用條件、基本解題步驟、及實現(xiàn)等幾個方面，結(jié)合了分治實戰(zhàn)，完整梳理算法內(nèi)容。

1. 算法思想

總體思想：

• 將要求解的較大規(guī)模的問題分割成k個更小規(guī)模的子問題。
• 對這k個子問題分別求解。如果子問題的規(guī)模仍然不夠小，則再劃分為k個子問題，如此遞歸的進行下去，直到問題規(guī)模足夠小，很容易求出其解為止。
• 將求出的小規(guī)模的問題的解合并為一個更大規(guī)模的問題的解，自底向上逐步求出原來問題的解。

分治的設計思想是，將一個難以直接解決的大問題，分割成一些規(guī)模較小的相同問題，以便各個擊破，分而治之。

2. 適用條件

分治所能解決的問題一般具有以下幾個特征：

• 該問題的規(guī)模縮小到一定的程度就可以容易地解決；
• 該問題可以分解為若干個規(guī)模較小的相同問題，即該問題具有最優(yōu)子結(jié)構(gòu)性質(zhì)
• 利用該問題分解出的子問題的解可以合并為該問題的解；
• 該問題所分解出的各個子問題是相互獨立的，即子問題之間不包含公共的子問題。

這條特征涉及到分治的效率，如果各子問題是不獨立的，則分治要做許多不必要的工作，重復地解公共的子問題，此時雖然也可用分治，但一般用動態(tài)規(guī)劃較好。

3. 基本步驟

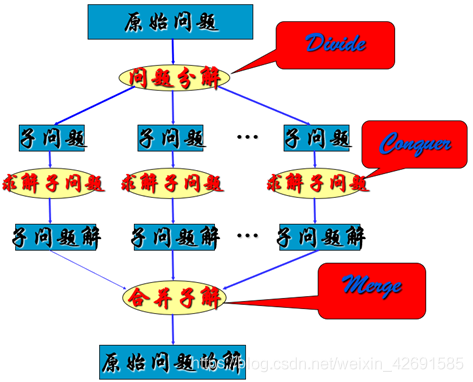
設計過程分為三個階段：

• Divide：整個問題劃分為多個子問題
• Conquer：求解各子問題(遞歸調(diào)用正設計的算法)
• Merge：合并子問題的解, 形成原始問題的解

偽代碼：

def divide_conquer(problem, paraml, param2,...)：
    # 不斷切分的終止條件
    if problem is None：
        print_result
        return
    # 準備數(shù)據(jù)
    data=prepare_data(problem)
    # 將大問題拆分為小問題
    subproblems=split_problem(problem, data)
    # 處理小問題，得到子結(jié)果
    subresult1=self.divide_conquer(subproblems[0],p1,..…)
    subresult2=self.divide_conquer(subproblems[1],p1,...)
    subresult3=self.divide_conquer(subproblems[2],p1,.…)
    # 對子結(jié)果進行合并 得到最終結(jié)果
    result=process_result(subresult1, subresult2, subresult3,...)

4. 時間復雜性分析

一般的，分治的時間復雜性可歸結(jié)為遞歸方程：

其中，a是子問題的個數(shù)，b是遞減的步長， ~表示遞減方式， D(n)是合成子問題的開銷。
??通常，遞歸元的遞減方式~有兩種：

1、減法，即n – b，的形式
2、除法，即n / b，的形式

5. 算法實現(xiàn)

如果用算法A處理一個計算問題，當輸入數(shù)據(jù)D是一個集合,其數(shù)據(jù)量比較大時,可以將D劃分為幾個子集D1,D2,…D，然后使用算法A分別處理這些子集,最后將k 個結(jié)果進行綜合,從而得到原問題的解。這種方法稱為分治。

用遞歸函數(shù)框架描述分治：

Divide_and conquer (D) {
If (集合 D的數(shù)據(jù)量非常小，達到遞歸起點)
    用非遞歸方法直接處理D, 得到解S;
else {
   將D分解為子集D, D.*, Dk;
   for (i =1;i <=k;i++ )
   Si= Divide_ and_ conquer (D：) ;
  綜合S,S2,...,Sk,得到解S;
}

分治的執(zhí)行步驟可以分為三個階段,即劃分數(shù)據(jù)階段、遞歸處理階段和綜合合并階段。有些問題的劃分階段時間費用較多,有些問題則合并階段的時間費用較多。

6. 應用與實例

分治算法的應用主要可分為以下五種：

1）二分搜索算法
????問題：要求在一個n元已排序的數(shù)組A[n]中，搜索一個特定元素x。

2）合并排序算法
????問題：將一個n元數(shù)組A排序。

3）快速排序算法
????問題：將一個n元數(shù)組A排序。

4）搜索第k元
????問題：n元數(shù)組A中,尋找大小排第k位的元素。

5）最近點對
????問題：空間n個點中,尋找距離最近的點對。

而通過應用舉例分析理解分治算法的原理其實并不難，但是要想靈活應用并在編程中體現(xiàn)這種思想中卻并不容易。所以，這里這里用分治算法應用在排序的時候的一個例子，加深對分治算法的理解。

相關概念：

? 有序度：表示一組數(shù)據(jù)的有序程度
? 逆序度：表示一組數(shù)據(jù)的無序程度

一般通過計算有序?qū)蛘吣嫘驅(qū)Φ膫€數(shù)，來表示數(shù)據(jù)的有序度或逆序度。

假設我們有 n 個數(shù)據(jù)，我們期望數(shù)據(jù)從小到大排列，那完全有序的數(shù)據(jù)的有序度就是 n(n-1)/2，逆序度等于 0；相反，倒序排列的數(shù)據(jù)的有序度就是 0，逆序度是 n(n-1)/2。

Q：如何編程求出一組數(shù)據(jù)的有序?qū)€數(shù)或者逆序?qū)€數(shù)呢？

因為有序?qū)€數(shù)和逆序?qū)€數(shù)的求解方式是類似的，所以這里可以只思考逆序?qū)Γǔ＝佑|的）個數(shù)的求解方法。

方法1：

• 拿數(shù)組里的每個數(shù)字跟它后面的數(shù)字比較，看有幾個比它小的。
• 把比它小的數(shù)字個數(shù)記作 k，通過這樣的方式，把每個數(shù)字都考察一遍之后，然后對每個數(shù)字對應的 k 值求和 o 最后得到的總和就是逆序?qū)€數(shù)。
• 這樣操作的時間復雜度是O(n^2)（需要兩層循環(huán)過濾）。那有沒有更加高效的處理方法呢？這里嘗試套用分治的思想來求數(shù)組 A 的逆序?qū)€數(shù)。

方法2：

• 首先將數(shù)組分成前后兩半 A1 和 A2，分別計算 A1 和 A2 的逆序?qū)€數(shù) K1 和 K2
• 然后再計算 A1 與 A2 之間的逆序?qū)€數(shù) K3。那數(shù)組 A 的逆序?qū)€數(shù)就等于 K1+K2+K3。
• 注意使用分治算法其中一個要求是，子問題合并的代價不能太大，否則就起不了降低時間復雜度的效果了。
• 如何快速計算出兩個子問題 A1 與 A2 之間的逆序?qū)€數(shù)呢？這里就要借助歸并排序算法了。（這里先回顧一下歸并排序思想）**如何借助歸并排序算法來解決呢？歸并排序中有一個非常關鍵的操作，就是將兩個有序的小數(shù)組，合并成一個有序的數(shù)組。實際上，在這個合并的過程中，可以計算這兩個小數(shù)組的逆序?qū)€數(shù)了。每次合并操作，我們都計算逆序?qū)€數(shù)，把這些計算出來的逆序?qū)€數(shù)求和，就是這個數(shù)組的逆序?qū)€數(shù)了。

7. 分治實戰(zhàn)

案例1：169.多數(shù)元素

【題目描述】

給定一個大小為 n 的數(shù)組，找到其中的眾數(shù)。眾數(shù)是指在數(shù)組中出現(xiàn)次數(shù)大于 [n/2] 的元素。
你可以假設數(shù)組是非空的，并且給定的數(shù)組總是存在眾數(shù)。

示例 1：
輸入：[3,2,3]
輸出：3

示例 2：
輸入：[2,2,1,1,1,2,2]
輸出：2

【解題思路】

• 確定切分的終止條件
  ??直到所有的子問題都是長度為 1 的數(shù)組，停止切分。
• 準備數(shù)據(jù)，將大問題切分為小問題
  ??遞歸地將原數(shù)組二分為左區(qū)間與右區(qū)間，直到最終的數(shù)組只剩下一個元素，將其返回
• 處理子問題得到子結(jié)果，并合并

• 長度為 1 的子數(shù)組中唯一的數(shù)顯然是眾數(shù)，直接返回即可。
• 如果它們的眾數(shù)相同，那么顯然這一段區(qū)間的眾數(shù)是它們相同的值。
• 如果他們的眾數(shù)不同，比較兩個眾數(shù)在整個區(qū)間內(nèi)出現(xiàn)的次數(shù)來決定該區(qū)間的眾數(shù)

【參考代碼】

class Solution(object)：
    def majorityElement2(self, nums)：
       """
        ：type nums：List[int]
        ：rtype：int
        """
        # 【不斷切分的終止條件】
        if not nums：
            return None
        if len(nums) == 1：
            return nums[0]
        # 【準備數(shù)據(jù)，并將大問題拆分為小問題】
        left = self.majorityElement(nums[：len(nums)//2])
        right = self.majorityElement(nums[len(nums)//2：])
        # 【處理子問題，得到子結(jié)果】
        # 【對子結(jié)果進行合并 得到最終結(jié)果】
        if left == right：
            return left
        if nums.count(left) > nums.count(right)：
            return left
        else：
            return right    

1）解法1（時間復雜度O（n）的解法）

遍歷nums，遇到與當前值相同count加一，不同count減一，并且當count減到0時，換當前數(shù)字為當前值，count置1

class Solution:
    def majorityElement(self, nums) -> int:
        cur = nums[0]
        count = 0
        for _ in nums:
            if cur == _:
                count += 1
            else:
                count -= 1
                if count == 0:
                    cur = _
                    count = 1

        return cur

2）解法2（哈希表）

統(tǒng)計頻次

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        numDict = {}
        n = len(nums)
        for i in nums:
            numDict[i] = numDict.get(i, 0) + 1
        for key in numDict.keys():
            if numDict[key] > n/2:
                return key

案例2：53.最大子序和

【題目描述】

給定一個整數(shù)數(shù)組 nums ，找到一個具有最大和的連續(xù)子數(shù)組（子數(shù)組最少包含一個元素），返回其最大和。

示例：
輸入：[-2,1,-3,4,-1,2,1,-5,4],
輸出：6
解釋：連續(xù)子數(shù)組 [4,-1,2,1] 的和最大為6。

【解題思路】

• 確定切分的終止條件
  ??直到所有的子問題都是長度為 1 的數(shù)組，停止切分。
• 準備數(shù)據(jù)，將大問題切分為小問題
  ??遞歸地將原數(shù)組二分為左區(qū)間與右區(qū)間，直到最終的數(shù)組只剩下一個元素，將其返回
• 處理子問題得到子結(jié)果，并合并

• 將數(shù)組切分為左右區(qū)間
• 對與左區(qū)間：從右到左計算左邊的最大子序和
• 對與右區(qū)間：從左到右計算右邊的最大子序和
• 由于左右區(qū)間計算累加和的方向不一致，因此，左右區(qū)間直接合并相加之后就是整個區(qū)間的和
• 最終返回左區(qū)間的元素、右區(qū)間的元素、以及整個區(qū)間(相對子問題)和的最大值

【參考代碼】

class Solution(object)：
    def maxSubArray(self, nums)：
        """
        ：type nums：List[int]
        ：rtype：int
        """
        # 【確定不斷切分的終止條件】
        n = len(nums)
        if n == 1：
            return nums[0]

        # 【準備數(shù)據(jù)，并將大問題拆分為小的問題】
        left = self.maxSubArray(nums[：len(nums)//2])
        right = self.maxSubArray(nums[len(nums)//2：])

        # 【處理小問題，得到子結(jié)果】
        #　從右到左計算左邊的最大子序和
        max_l = nums[len(nums)//2 -1] # max_l為該數(shù)組的最右邊的元素
        tmp = 0 # tmp用來記錄連續(xù)子數(shù)組的和
        
        for i in range( len(nums)//2-1 , -1 , -1 )：# 從右到左遍歷數(shù)組的元素
            tmp += nums[i]
            max_l = max(tmp ,max_l)
            
        # 從左到右計算右邊的最大子序和
        max_r = nums[len(nums)//2]
        tmp = 0
        for i in range(len(nums)//2,len(nums))：
            tmp += nums[i]
            max_r = max(tmp,max_r)
            
        # 【對子結(jié)果進行合并 得到最終結(jié)果】
        # 返回三個中的最大值
        return max(left,right,max_l+ max_r)

1）解法1（暴力求解）

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        tmp = nums[0]
        max_ = tmp
        n = len(nums)
        for i in range(1,n):
            # 當當前序列加上此時的元素的值大于tmp的值，說明最大序列和可能出現(xiàn)在后續(xù)序列中，記錄此時的最大值
            if tmp + nums[i]>nums[i]:
                max_ = max(max_, tmp+nums[i])
                tmp = tmp + nums[i]
            else:
            #當tmp(當前和)小于下一個元素時，當前最長序列到此為止。以該元素為起點繼續(xù)找最大子序列,
            # 并記錄此時的最大值
                max_ = max(max_, tmp, tmp+nums[i], nums[i])
                tmp = nums[i]
        return max_

2）解法2（分治法）

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        tmp = nums[0]
        max_ = tmp
        n = len(nums)
        for i in range(1,n):
            # 當當前序列加上此時的元素的值大于tmp的值，說明最大序列和可能出現(xiàn)在后續(xù)序列中，記錄此時的最大值
            if tmp + nums[i]>nums[i]:
                max_ = max(max_, tmp+nums[i])
                tmp = tmp + nums[i]
            else:
            #當tmp(當前和)小于下一個元素時，當前最長序列到此為止。以該元素為起點繼續(xù)找最大子序列,
            # 并記錄此時的最大值
                max_ = max(max_, tmp, tmp+nums[i], nums[i])
                tmp = nums[i]
        return max_

3）解法3（動態(tài)規(guī)劃）

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        dp=[0]*(len(nums))
        dp[0]=nums[0]
        for i in range(1,len(nums)):
            if dp[i-1]<=0:
                dp[i]=nums[i]
            else:
                dp[i]=dp[i-1]+nums[i]
        return max(dp)

案例3：50.Pow(x, n)

【題目描述】

實現(xiàn) pow(x, n) ，即計算 x 的 n 次冪函數(shù)。

示例 1：
輸入：2.00000, 10
輸出：1024.00000

示例 2：
輸入：2.10000, 3
輸出：9.26100

示例 3：
輸入：2.00000, -2
輸出：0.25000
解釋：2-2 = 1/22 = 1/4 = 0.25

【說明】

• 100.0 < x < 100.0 n 是 32 位有符號整數(shù)，其數(shù)值范圍是 [?2^{31}, 2^{31} ? 1] 。

【解題思路】

• 確定切分的終止條件
  ??對n不斷除以2，并更新n，直到為0，終止切分
• 準備數(shù)據(jù)，將大問題切分為小問題
  ??對n不斷除以2，更新
• 處理子問題得到子結(jié)果，并合并

• x與自身相乘更新x
• 如果n%2 ==1
• 將p乘以x之后賦值給p(初始值為1)，返回p

• 最終返回p

【參考代碼】

class Solution(object)：
    def myPow(self, x, n)：
        """
        ：type x：float
        ：type n：int
        ：rtype：float
        """
        # 處理n為負的情況
        if n < 0 ：
            x = 1/x
            n = -n
        # 【確定不斷切分的終止條件】
        if n == 0 ：
            return 1

        # 【準備數(shù)據(jù)，并將大問題拆分為小的問題】
        if n%2 ==1：
          # 【處理小問題，得到子結(jié)果】
          p = x * self.myPow(x,n-1)# 【對子結(jié)果進行合并 得到最終結(jié)果】
          return p
        return self.myPow(x*x,n/2)  

1）解法1（二分法）

class Solution:
    def myPow(self, x: float, n: int) -> float:
        if x == 0.0: return 0.0
        res = 1
        if n < 0: x, n = 1 / x, -n
        while n:
            if n & 1: res *= x
            x *= x
            n >>= 1
        return res

2）解法2（優(yōu)化遞歸）

class Solution(object):
    def myPow(self, x, n):
        """
        :type x: float
        :type n: int
        :rtype: float
        """
        if n == 0:
            return 1
        if n < 0:
            x = 1 / x
            n = -n
        if n % 2:
            return x * self.myPow(x, n - 1)
        return self.myPow(x * x, n / 2)

參考資料

1. 編程實踐（LeetCode 分類練習）

2. 力扣(LeetCode)平臺