正態(tài)分布對(duì)數(shù)據(jù)分析很重要！

轉(zhuǎn)自：機(jī)器之心

大家好，我是寶器。

我們從高中就開始學(xué)正態(tài)分布，現(xiàn)在做數(shù)據(jù)分析、機(jī)器學(xué)習(xí)還是離不開它，那你有沒有想過正態(tài)分布有什么特別之處？為什么那么多關(guān)于數(shù)據(jù)科學(xué)和機(jī)器學(xué)習(xí)的文章都圍繞正態(tài)分布展開？本文作者專門寫了一篇文章，試著用易于理解的方式闡明正態(tài)分布的概念。

機(jī)器學(xué)習(xí)的世界是以概率分布為中心的，而概率分布的核心是正態(tài)分布。本文說明了什么是正態(tài)分布，以及為什么正態(tài)分布的使用如此廣泛，尤其是對(duì)數(shù)據(jù)科學(xué)家和機(jī)器學(xué)習(xí)專家來說。

我會(huì)從最基礎(chǔ)的內(nèi)容開始解釋，以便讀者們理解為什么正態(tài)分布如此重要。

文章結(jié)構(gòu)如下：

• 什么是概率分布？

• 什么是正態(tài)分布？

• 為什么變量如此青睞正態(tài)分布

• 如何用 Python 查看查看特征的分布？

• 其它分布變一變也能近似正態(tài)分布

先讓我們來看一點(diǎn)背景知識(shí)：

1. 首先，要注意的最重要的一點(diǎn)是，正態(tài)分布也被稱為高斯分布。

2. 它是以天才卡爾·弗里德里希·高斯（Carl Friedrich Gauss）的名字命名的。

3. 最后需要注意的是，簡單的預(yù)測模型一般都是最常用的模型，因?yàn)樗鼈円子诮忉專惨子诶斫狻，F(xiàn)在補(bǔ)充一點(diǎn)：正態(tài)分布因?yàn)楹唵味餍小?/span>

因此，正態(tài)概率分布很值得我們?nèi)セ〞r(shí)間了解。

什么是概率分布？

想象我們正在自己的數(shù)據(jù)科學(xué)項(xiàng)目中構(gòu)建感興趣的預(yù)測模型：

• 如果我們想準(zhǔn)確地預(yù)測變量，那么首先我們要了解目標(biāo)變量的基本行為。
• 我們先要確定目標(biāo)變量可能輸出的結(jié)果，以及這個(gè)可能的輸出結(jié)果是離散值（孤立值）還是連續(xù)值（無限值）。簡單點(diǎn)解釋就是，如果我們要評(píng)估骰子的行為，那么第一步是要知道它可以取 1 到 6 之間的任一整數(shù)值（離散值）。
• 然后下一步是開始為事件（值）分配概率。因此，如果一個(gè)值不會(huì)出現(xiàn)，則概率為 0%。

概率越高，事件發(fā)生的可能性就越大。

舉個(gè)例子，我們可以大量重復(fù)一個(gè)實(shí)驗(yàn)，并記錄我們檢索到的變量值，這樣概率分布就會(huì)慢慢展現(xiàn)在我們的面前。

每次實(shí)驗(yàn)產(chǎn)生一個(gè)值，這些值可以分配到類別/桶中了。對(duì)每個(gè)桶來說，我們可以記錄變量值出現(xiàn)在桶里的次數(shù)。例如，我們可以扔 10,000 次骰子，每次骰子會(huì)產(chǎn)生 6 個(gè)可能的值，我們可以創(chuàng)建 6 個(gè)桶。并記錄每個(gè)值出現(xiàn)的次數(shù)。

我們可以根據(jù)這些值作圖。所作曲線就是概率分布曲線，目標(biāo)變量得到一個(gè)值的概率就是該變量的概率分布。

理解了值的分布方式后，就可以開始估計(jì)事件的概率了，甚至可以使用公式（概率分布函數(shù)）。因此，我們可以更好地理解它的行為。概率分布依賴于樣本的矩，比如平均值、標(biāo)準(zhǔn)差、偏度及峰度。如果對(duì)所有概率求和，總和為 100%。

現(xiàn)實(shí)世界中存在很多概率分布，最常用的是「正態(tài)分布」。

什么是正態(tài)概率分布?

如果對(duì)概率分布作圖，得到一條倒鐘形曲線，樣本的平均值、眾數(shù)以及中位數(shù)是相等的，那么該變量就是正態(tài)分布的。

這是正態(tài)分布鐘形曲線的示例：

上面是一個(gè)變量的高斯分布圖形，像神經(jīng)網(wǎng)絡(luò)那樣上百萬的參數(shù)量，每個(gè)參數(shù)都有自己獨(dú)立的分布形狀，還有極其恐怖的聯(lián)合分布形狀。這種高維聯(lián)合分布就主導(dǎo)了不同任務(wù)的表現(xiàn)，因此理解和估計(jì)目標(biāo)變量的概率分布是很重要的。

以下變量非常接近正態(tài)分布：

1. 人群的身高

2. 成年人的血壓

3. 擴(kuò)散后的粒子的位置

4. 測量誤差

5. 人群的鞋碼

6. 員工回家所需時(shí)間

此外，我們周圍的大部分變量都呈置信度為 x% 的正態(tài)分布（x<100）。所以說，生活中經(jīng)常出現(xiàn)的各種變量，差不多都能用高斯分布描述。

好理解的正態(tài)分布

正態(tài)分布是只依賴數(shù)據(jù)集中兩個(gè)參數(shù)的分布，這兩個(gè)參數(shù)分別是：樣本的平均值和標(biāo)準(zhǔn)差。

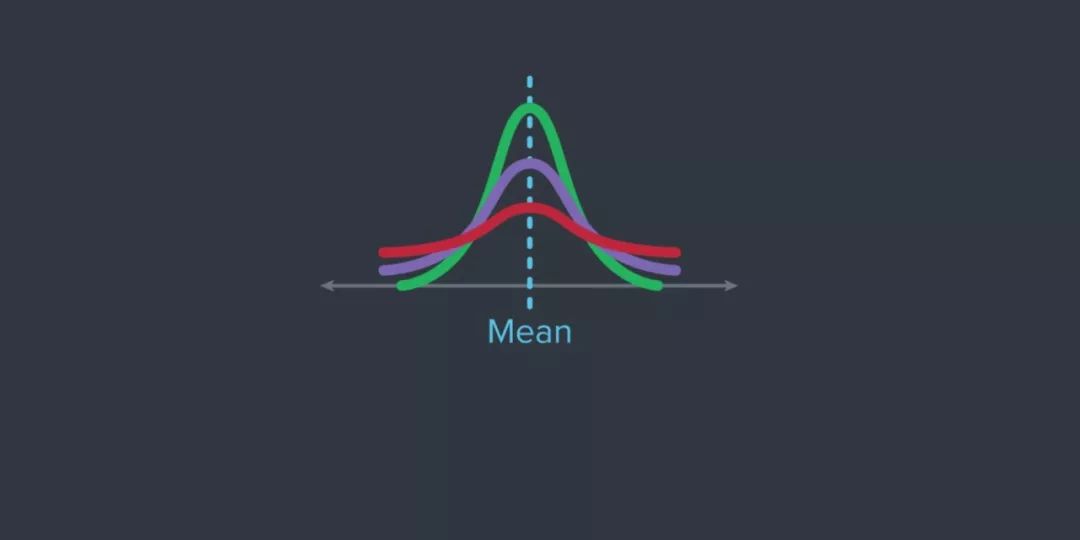
• 平均值——樣本中所有點(diǎn)的平均值。

• 標(biāo)準(zhǔn)差——表示數(shù)據(jù)集與樣本均值的偏離程度。

分布的這一特性讓統(tǒng)計(jì)人員省事不少，因此預(yù)測任何呈正態(tài)分布的變量準(zhǔn)確率通常都很高。值得注意的是，一旦你研究過自然界中大多數(shù)變量的概率分布，你會(huì)發(fā)現(xiàn)它們都大致遵循正態(tài)分布。

正態(tài)分布很好解釋。因?yàn)椋?/span>

1. 分布的均值、眾數(shù)和中位數(shù)是相等的；

2. 我們只要用平均值和標(biāo)準(zhǔn)差就可以解釋整個(gè)分布。

為什么這么多變量近似正態(tài)分布？

為什么樣本一多，那么總會(huì)有一堆樣本都非常普通？這個(gè)想法背后有這樣一個(gè)定理：你在大量隨機(jī)變量上多次重復(fù)一個(gè)實(shí)驗(yàn)時(shí)，它們的分布總和將非常接近正態(tài)性（normality）。

人的身高是一個(gè)基于其他隨機(jī)變量（比如一個(gè)人所消耗的營養(yǎng)量、他們居住的環(huán)境以及他們的基因等）的隨機(jī)變量，這些隨機(jī)變量的分布總和最終是非常接近正態(tài)的。這就是中心極限定理。

我們從前文了解到，正態(tài)分布是許多隨機(jī)分布的和。如果我們對(duì)正態(tài)分布密度函數(shù)作圖，那所作曲線有如下特性：

這個(gè)鐘形曲線平均值為 100，標(biāo)準(zhǔn)差為 1。

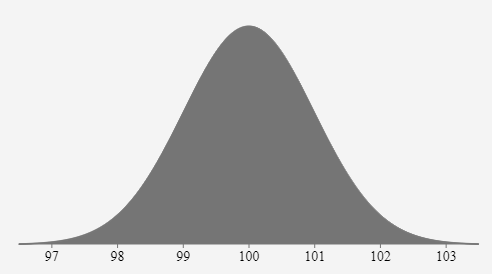
• 平均值是曲線的中心。這是曲線的最高點(diǎn)，因?yàn)榇蠖鄶?shù)點(diǎn)都在平均值附近；
  
• 曲線兩側(cè)點(diǎn)的數(shù)量是相等的。曲線中心的點(diǎn)數(shù)量最多；
• 曲線下的面積是變量能取的所有值的概率和；
• 因此曲線下面的總面積為 100%。

上圖介紹了非常出名的 3σ原則，即：

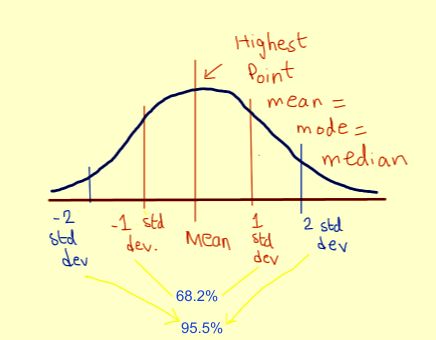
• 約有 68.2% 的點(diǎn)落在 ±1 個(gè)標(biāo)準(zhǔn)差的范圍內(nèi)
  
• 約有 95.5% 的點(diǎn)落在 ±2 個(gè)標(biāo)準(zhǔn)差的范圍內(nèi)
• 約有 99.7% 的點(diǎn)落在 ±3 個(gè)標(biāo)準(zhǔn)差的范圍內(nèi)。

這樣我們就可以輕松地估計(jì)出變量的波動(dòng)性，還可以給出一個(gè)置信水平，估計(jì)它可能取的值是多少。例如，在上面的灰色鐘型曲線中，變量值出現(xiàn)在 101~99 之間的概率約為 68.2%。想象一下，當(dāng)你根據(jù)這樣的信息做決定時(shí)，你的信心有多充足。

概率分布函數(shù)

正態(tài)分布的概率密度函數(shù)是：

概率密度函數(shù)本質(zhì)上是連續(xù)隨機(jī)變量取某些值的概率。例如想知道變量出現(xiàn)在 0 到 1 之間，它的概率就能通過概率密度函數(shù)求出。

• 如果你用計(jì)算好的概率密度函數(shù)繪制概率分布曲線，那么給定范圍的曲線下的面積就描述了目標(biāo)變量在該范圍內(nèi)的概率。
  
• 概率分布函數(shù)是根據(jù)多個(gè)參數(shù)（如變量的平均值或標(biāo)準(zhǔn)差）計(jì)算得到的。
• 我們可以用概率分布函數(shù)求出隨機(jī)變量在一個(gè)范圍內(nèi)取值的相對(duì)概率。舉個(gè)例子，我們可以記錄股票的日收益，把它們分到合適的桶中，然后找出未來收益概率在 20~40% 的股票。
• 標(biāo)準(zhǔn)差越大，樣本波動(dòng)越大。

如何用 Python 找出特征分布？

我用過的最簡單的方法是在 Pandas 的 DataFrame 中加載所有特征，然后直接調(diào)用它的方法找出特征的概率分布：

這里的 bins 表示分布的柱狀數(shù)量。當(dāng)然上面并不是一個(gè)正態(tài)分布，那么當(dāng)變量滿足正態(tài)分布時(shí)，它意味著什么？

這意味著，如果你把大量分布不同的隨機(jī)變量加在一起，你的新變量最終也服從正態(tài)分布，這就是中心極限定理的魅力。此外，服從正態(tài)分布的變量會(huì)一直服從正態(tài)分布。舉個(gè)例子，如果 A 和 B 是兩個(gè)服從正態(tài)分布的變量，那么：

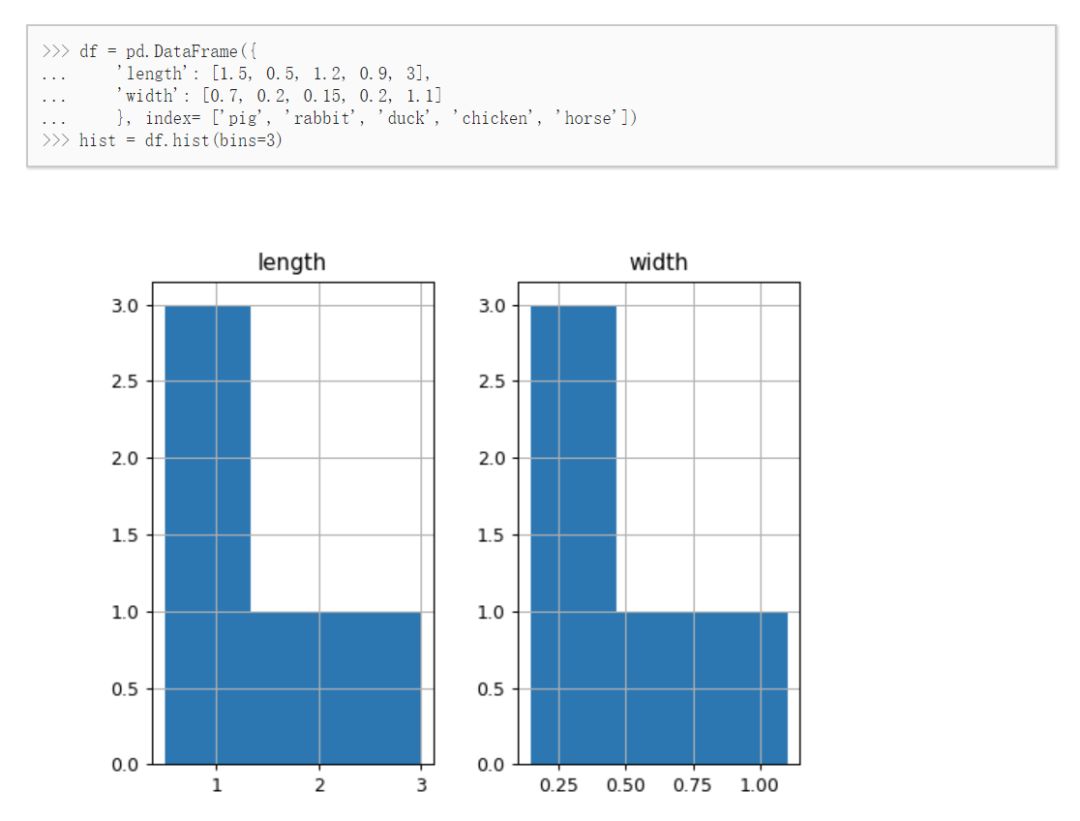
• AxB 服從正態(tài)分布；
  
• A+B 服從正態(tài)分布。

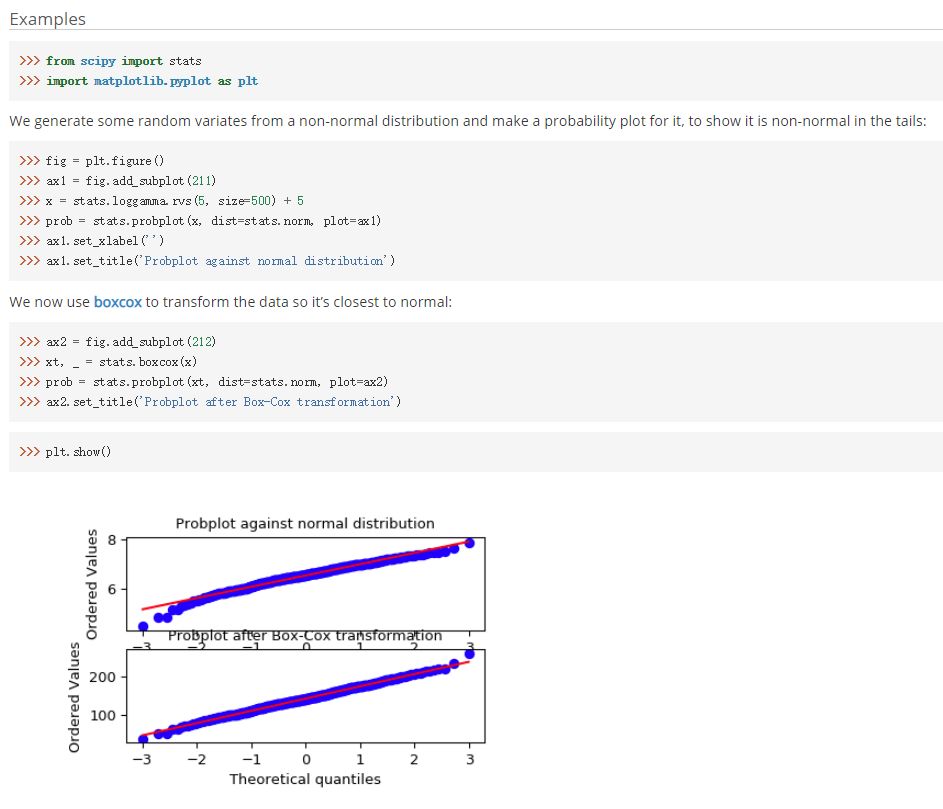
變量還是乖乖地變成正態(tài)分布吧

如果樣本滿足某個(gè)未知的分布，那么通過一系列操作，它總是能變成正態(tài)分布。關(guān)于變換的方法可參考這篇：正態(tài)分布在機(jī)器學(xué)習(xí)中為何如此重要？

相反，標(biāo)準(zhǔn)正態(tài)分布的疊加與轉(zhuǎn)換，也一定能變化為任意未知分布。從標(biāo)準(zhǔn)正態(tài)轉(zhuǎn)換到未知分布，就是很多機(jī)器學(xué)習(xí)模型希望做到的，不論是視覺中的 VAE 或 GAN，還是其它領(lǐng)域的模型。

但對(duì)于傳統(tǒng)統(tǒng)計(jì)學(xué)，我們更希望將特征的分布轉(zhuǎn)換成正態(tài)分布，因?yàn)檎龖B(tài)分布簡單又好算呀。下面展示了幾種轉(zhuǎn)換為標(biāo)準(zhǔn)正態(tài)的方法，像相信變換什么的，在高中都有學(xué)過。

1. 線性變換

我們收集到作為變量的樣本后，就可以用下面的公式對(duì)樣本做線性變換，從而計(jì)算出?

• Z 分?jǐn)?shù)
• 計(jì)算平均值
• 計(jì)算標(biāo)準(zhǔn)差

用下式根據(jù)每一個(gè)值 x 計(jì)算出 Z

以前 x 可能服從某個(gè)未知分布，但是歸一化后的 Z 是服從正態(tài)分布的。嗯，這就是做批量歸一化或其它歸一化的好處吧。

2.Box-cox 變換

你可以用 Python 的 SciPy 包將數(shù)據(jù)轉(zhuǎn)換成正態(tài)分布：

scipy.stats.boxcox(x,?lmbda=None,?alpha=None)

3.YEO-JOHBSON 變換

此外，也可以用強(qiáng)大的 yeo-johnson 變換。Python 的 sci-kit learn 提供了合適的函數(shù)：

sklearn.preprocessing.PowerTransformer(method=’yeo-johnson’,?standardize=True,?copy=True)

最后，非常重要的一點(diǎn)是，在沒有做任何分析的情況下假設(shè)變量服從正態(tài)分布是很不明智的。

以遵循泊松分布（Poisson distribution）、t 分布（student-t 分布）或二項(xiàng)分布（Binomial distribution）的樣本為例，如果錯(cuò)誤地假設(shè)變量服從正態(tài)分布可能會(huì)得到錯(cuò)誤的結(jié)果。

原文鏈接：https://medium.com/fintechexplained/ever-wondered-why-normal-distribution-is-so-important-110a482abee3

·················END·················

推薦閱讀

1. 我在字節(jié)做了哪些事
   

2. 寫給所有數(shù)據(jù)人。

3. 從留存率業(yè)務(wù)案例談0-1的數(shù)據(jù)指標(biāo)體系

4. 數(shù)據(jù)分析師的一周
   

5. 超級(jí)菜鳥如何入門數(shù)據(jù)分析？
   

歡迎長按掃碼關(guān)注「數(shù)據(jù)管道」