JavaScript浮點數(shù)陷阱,你需要了解一下

來源 |?http://www.fly63.com/article/detial/10056
浮點數(shù)的存儲
符號位S:第 1 位是正負(fù)數(shù)符號位(sign),0代表正數(shù),1代表負(fù)數(shù) 指數(shù)位E:中間的 11 位存儲指數(shù)(exponent),用來表示次方數(shù) 尾數(shù)位M:最后的 52 位是尾數(shù)(mantissa),超出的部分自動進(jìn)一舍零

實際數(shù)字就可以用以下公式來計算:
$ V = (-1)^{S}\times M \times 2^{E} $
注意以上的公式遵循科學(xué)計數(shù)法的規(guī)范,在十進(jìn)制是為0
最終的公式變成:
$ V = (-1)^{S}\times (M+1) \times 2^{E-1023} $
所以 4.5 最終表示為(M=001、E=1025):

?下面再以?0.1 例解釋浮點誤差的原因,?0.1 轉(zhuǎn)成二進(jìn)制表示為?0.0001100110011001100(1100循環(huán)),1.100110011001100x2^-4,所以 E=-4+1023=1019;M 舍去首位的1,得到 100110011...。最終就是:

轉(zhuǎn)化成十進(jìn)制后為?0.100000000000000005551115123126,因此就出現(xiàn)了浮點誤差。
為什么?0.1+0.2=0.30000000000000004?
計算步驟為:
// 0.1 和 0.2 都轉(zhuǎn)化成二進(jìn)制后再進(jìn)行運算0.00011001100110011001100110011001100110011001100110011010 +0.0011001100110011001100110011001100110011001100110011010 =0.0100110011001100110011001100110011001100110011001100111// 轉(zhuǎn)成十進(jìn)制正好是 0.30000000000000004
為什么 x=0.1 能得到?0.1?
恭喜你到了看山不是山的境界。因為 mantissa 固定長度是 52 位,再加上省略的一位,最多可以表示的數(shù)是 2^53=9007199254740992,對應(yīng)科學(xué)計數(shù)尾數(shù)是 9.007199254740992,這也是?js?最多能表示的精度。它的長度是 16,所以可以使用 toPrecision(16)?來做精度運算,超過的精度會自動做湊整處理。于是就有:
0.10000000000000000555.toPrecision(16)// 返回 0.1000000000000000,去掉末尾的零后正好為 0.1// 但你看到的 `0.1` 實際上并不是 `0.1`。不信你可用更高的精度試試:0.1.toPrecision(21) = 0.100000000000000005551
大數(shù)危機(jī)
可能你已經(jīng)隱約感覺到了,如果整數(shù)大于 9007199254740992 會出現(xiàn)什么情況呢?
由于 E 最大值是 1023,所以最大可以表示的整數(shù)是 2^1024 - 1,這就是能表示的最大整數(shù)。但你并不能這樣計算這個數(shù)字,因為從 2^1024 開始就變成了 Infinity
> Math.pow(2, 1023)8.98846567431158e+307> Math.pow(2, 1024)Infinity
那么對于?(2^53, 2^63)?之間的數(shù)會出現(xiàn)什么情況呢?
(2^53, 2^54)?之間的數(shù)會兩個選一個,只能精確表示偶數(shù)
(2^54, 2^55)?之間的數(shù)會四個選一個,只能精確表示4個倍數(shù)
... 依次跳過更多2的倍數(shù)
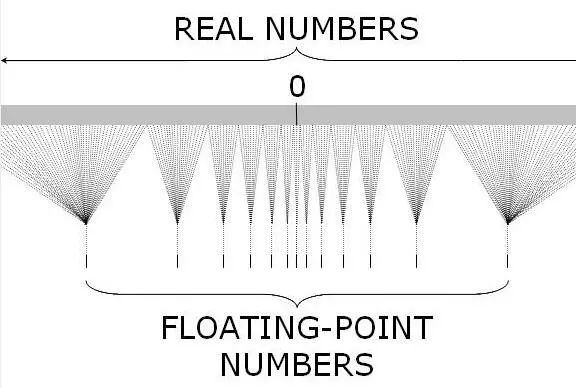
下面這張圖能很好的表示 JavaScript 中浮點數(shù)和實數(shù)(Real Number)之間的對應(yīng)關(guān)系。我們常用的?(-2^53, 2^53)?只是最中間非常小的一部分,越往兩邊越稀疏越不精確。
在淘寶早期的訂單系統(tǒng)中把訂單號當(dāng)作數(shù)字處理,后來隨意訂單號暴增,已經(jīng)超過了
9007199254740992,最終的解法是把訂單號改成字符串處理。
要想解決大數(shù)的問題你可以引用第三方庫 bignumber.js,原理是把所有數(shù)字當(dāng)作字符串,重新實現(xiàn)了計算邏輯,缺點是性能比原生的差很多。所以原生支持大數(shù)就很有必要了,現(xiàn)在 TC39 已經(jīng)有一個 Stage 3 的提案 proposal bigint,大數(shù)問題有問徹底解決。
toPrecision?vs?toFixed
數(shù)據(jù)處理時,這兩個函數(shù)很容易混淆。它們的共同點是把數(shù)字轉(zhuǎn)成字符串供展示使用。注意在計算的中間過程不要使用,只用于最終結(jié)果。
不同點就需要注意一下:
toPrecision 是處理精度,精度是從左至右第一個不為0的數(shù)開始數(shù)起。
toFixed 是小數(shù)點后指定位數(shù)取整,從小數(shù)點開始數(shù)起。
兩者都能對多余數(shù)字做湊整處理,也有些人用 toFixed 來做四舍五入,但一定要知道它是有 Bug 的。
如:1.005.toFixed(2)?返回的是 1.00?而不是 1.01。
原因:1.005 實際對應(yīng)的數(shù)字是 1.00499999999999989,在四舍五入時全部被舍去!
解法:使用專業(yè)的四舍五入函數(shù)?Math.round()?來處理。但 Math.round(1.005 * 100) / 100?還是不行,因為 1.005 * 100 = 100.49999999999999。還需要把乘法和除法精度誤差都解決后再使用 Math.round。可以使用后面介紹的 number-precision#round 方法來解決。
解決方案
回到最關(guān)心的問題:如何解決浮點誤差。首先,理論上用有限的空間來存儲無限的小數(shù)是不可能保證精確的,但我們可以處理一下得到我們期望的結(jié)果。
數(shù)據(jù)展示類
當(dāng)你拿到 1.4000000000000001 這樣的數(shù)據(jù)要展示時,建議使用 toPrecision 湊整并 parseFloat 轉(zhuǎn)成數(shù)字后再顯示,如下:
parseFloat(1.4000000000000001.toPrecision(12)) === 1.4 // True
封裝成方法就是:
function strip(num, precision = 12) {return +parseFloat(num.toPrecision(precision));}
為什么選擇 12 做為默認(rèn)精度?這是一個經(jīng)驗的選擇,一般選12就能解決掉大部分0001和0009問題,而且大部分情況下也夠用了,如果你需要更精確可以調(diào)高。
數(shù)據(jù)運算類
對于運算類操作,如?+-*/,就不能使用 toPrecision 了。正確的做法是把小數(shù)轉(zhuǎn)成整數(shù)后再運算。以加法為例:
/*** 精確加法*/function add(num1, num2) {const num1Digits = (num1.toString().split('.')[1] || '').length;const num2Digits = (num2.toString().split('.')[1] || '').length;const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits));return (num1 * baseNum + num2 * baseNum) / baseNum;}
以上方法能適用于大部分場景。遇到科學(xué)計數(shù)法如 2.3e+1(當(dāng)數(shù)字精度大于21時,數(shù)字會強(qiáng)制轉(zhuǎn)為科學(xué)計數(shù)法形式顯示)時還需要特別處理一下。
本文完?

