時(shí)間序列 ARMA 模型實(shí)戰(zhàn)!
ARMA全稱Autoregressive moving average model(自回歸滑動(dòng)平均模型),由美國統(tǒng)計(jì)學(xué)家博克斯(G.E.P.Box)和英國統(tǒng)計(jì)學(xué)家詹金斯(G.M.Jenkins)在二十世紀(jì)七十年代提出,也稱B-J方法。
ARMA模型有三種基本形式:
自回歸模型(AR,Auto-regressive)
自回歸模型根據(jù)歷史觀測值進(jìn)行預(yù)測。
其中,是預(yù)測誤差,為回歸系數(shù)。移動(dòng)平均模型(MA,Moving?Average)
移動(dòng)平均模型根據(jù)歷史預(yù)測誤差進(jìn)行預(yù)測。
其中,為前q期的隨機(jī)擾動(dòng)項(xiàng),誤差項(xiàng)是當(dāng)前期的隨機(jī)干擾(零均值白噪聲序列),為平滑系數(shù)。混合模型(ARMA,Auto-regressive Moving?Average)
混合模型為同時(shí)包含AR模型和MA模型。
自回歸不是多元線性回歸
小標(biāo)題中的多元線性回歸這里特指平時(shí)常說的帶有多個(gè)自變量的非時(shí)間序列多元線性回歸模型。
回歸模型:
其中,為因變量,為自變量,為待估計(jì)的參數(shù),為誤差項(xiàng)。
自回歸模型:
其中,為序列本身前個(gè)觀測值。
回歸是一種分析自變量和因變量關(guān)系的模型,當(dāng)因變量和自變量為線性關(guān)系時(shí)叫線性回歸模型,當(dāng)有多個(gè)變量時(shí)叫多元線性回歸模型。自回歸(AR)模型是一種特殊的多元線性回歸模型,和平時(shí)用的多元線性回歸模型略有不同。
多元線性回歸模型有多個(gè)自變量,但時(shí)間序列因其特殊性,一個(gè)時(shí)刻只有一個(gè)觀測值,在無其他維度數(shù)據(jù)補(bǔ)充的前提下,沒有可輔助預(yù)測的自變量,因而只能取其自身延遲p個(gè)時(shí)刻的觀測值作為自變量,所以稱自回歸。自回歸使用自身的數(shù)據(jù)進(jìn)行預(yù)測,序列前后應(yīng)當(dāng)有相關(guān)性。所以多元線性回歸模型預(yù)測時(shí)并不要求序列平穩(wěn),但AR模型則要求序列必須是平穩(wěn)的。
AR模型對平穩(wěn)性要求體現(xiàn)在如下幾個(gè)方面:
| 均值 | 常數(shù) |
| 方差 | 常數(shù) |
| ACF | 拖尾 |
| PACF | p階截尾 |
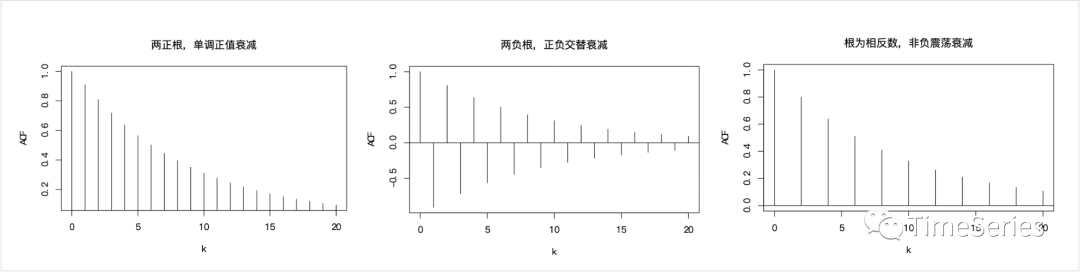
對于一般的AR(p)模型,其ACF的性質(zhì)以及序列的隨機(jī)周期,也由其特征根決定。ACF可以是單調(diào)衰減、震蕩衰 減、正負(fù)交替衰減、呈周期震蕩衰減。在有復(fù)特征根根或者有接近?1的特征根時(shí)時(shí)間序列呈現(xiàn)出一定的隨機(jī)周期變化。
下面是AR(2)模型對不同取值畫出ACF的典型圖形,供參考:
偏自相關(guān)函數(shù)p階截尾表明,變量只與前p個(gè)變量有關(guān),因而也可以借助PACF確定AR模型的階數(shù)p。
比如可以畫出PACF圖的上下界限,以此判斷PACF在哪里截尾。
上圖中PACF雖然在k=3,9,14,16等位置超出界限,但是超出不多,可考慮用 AR(3) 建模。
移動(dòng)平均不是移動(dòng)平滑
在之前的文章中我們已經(jīng)講過了簡單移動(dòng)平均(SMA)、加權(quán)移動(dòng)平均(WMA)、指數(shù)移動(dòng)平均(EMA),他們和指數(shù)平滑一樣都可以認(rèn)為是一種平滑方法,利用修勻技術(shù)消弱短期隨機(jī)波動(dòng)對序列的影響使序列平滑化。
而ARMA中的MA模型,關(guān)注的是自回歸模型中誤差項(xiàng)的累加,基于移動(dòng)平均的特性,能有效地消除預(yù)測中的隨機(jī)波動(dòng)。MA模型是用于預(yù)測未來值的方法,而移動(dòng)平均平滑法是用來估計(jì)歷史值的循環(huán)趨勢。
MA(q)模型結(jié)構(gòu)如下:
其中,為前q期的隨機(jī)擾動(dòng)項(xiàng),誤差項(xiàng)是當(dāng)前期的隨機(jī)干擾(零均值白噪聲序列),為序列均值,為平滑系數(shù)且為待優(yōu)化的參數(shù)。
殘差序列怎么來的?如下公式遞歸計(jì)算出來的。
其中,為序列均值,需要估算。
貼個(gè)參考鏈接:https://stats.stackexchange.com/questions/26024/moving-average-model-error-terms
MA模型認(rèn)為主要是受過去q期的誤差項(xiàng)的影響。對于高階的AR模型,有些可以用低階的MA模型更好地描述。一般的AR模型也可以用高階MA模型近似。MA模型同樣要求序列寬平穩(wěn)。
MA模型的自相關(guān)函數(shù)具有截尾性,即自相關(guān)函數(shù)在k>q后為零。
| ACF | 拖尾 |
| PACF | p階截尾 |
示例:
上圖ACF在k=1很大,在k=3和k=9也比較明顯,可以考慮擬合 MA(3) 或 MA(9)。
回歸配平均效果翻倍
AR模型有偏自相關(guān)函數(shù)截尾性質(zhì),MA模型有相關(guān)函數(shù)截尾性質(zhì)。ARMA模型結(jié)合了AR和MA模型,在對數(shù)據(jù)擬合優(yōu)度相近的情況下往往可以得到更好的模型,而且不要求偏自相關(guān)函數(shù)截尾也不要求相關(guān)函數(shù)截尾。
ARMA模型的公式也很直接,AR模型+MA模型:
以上可以看出的取值是前p期和前q期的多元線性函數(shù)。
q=0時(shí)為AR(p)模型可以看成ARMA(p, 0),p=0時(shí)為MA(q)模型可以看成是ARMA(0, q)。
| AR(p) | 拖尾 | p階截尾 |
| MA(q) | q階截尾 | 拖尾 |
| ARMA(p,q) | 拖尾 | 拖尾 |
眾里尋參千百度
實(shí)際用ARMA建模時(shí),階數(shù)p、q都是未知的,確定p、q的問題稱為定階,一般畫自相關(guān)偏自相關(guān)圖或者根據(jù)最優(yōu)信息準(zhǔn)則定階。
上文中已經(jīng)給出了第一種判斷方式,即根據(jù)ACF和PACF圖確定。但是有時(shí)肉眼判斷會(huì)產(chǎn)生困擾,看不清晰多少階截尾且需要主觀判斷。此時(shí)就可以根據(jù)最優(yōu)信息準(zhǔn)則選擇p、q,篩選策略為盡可能選擇更簡單的模型。常用最優(yōu)信息準(zhǔn)則有AIC、BIC。
AIC(Akaike information criterion,赤池信息量準(zhǔn)則),由日本統(tǒng)計(jì)學(xué)家Akaike于1973年提出,綜合考慮擬合精度和模型參數(shù)個(gè)數(shù),值越小越好。
其中,k表示模型參數(shù)的個(gè)數(shù),L表示似然函數(shù)。
k好說為參數(shù)個(gè)數(shù)為p+q+1;L似然函數(shù)怎么理解,在機(jī)器學(xué)習(xí)中經(jīng)常用到這個(gè)概念,希望預(yù)測結(jié)果和實(shí)際值越接近越好(長得越像越好),當(dāng)前場景下可以簡記為負(fù)的殘差平方和,L越大擬合越精確。網(wǎng)上看到的一段公式:
BIC(Bayesian information criterion,Bayesian information criterion)是由Schwarz在1978年提出,公式和AIC基本一致,僅在懲罰項(xiàng)中增加了樣本數(shù)量的考量。
為何?因?yàn)锳IC雖好卻有不足,就是樣本量大的場景下,AIC準(zhǔn)則通常愿意選擇更復(fù)雜的模型,即便實(shí)際模型復(fù)雜度很低。原因體現(xiàn)在AIC的懲罰項(xiàng)為參數(shù)個(gè)數(shù)和樣本容量沒關(guān)系,但是似然函數(shù)卻會(huì)受到樣本容量的放大。
BIC考慮了樣本個(gè)數(shù),懲罰項(xiàng)比AIC更大,樣本數(shù)量過多時(shí),可以防止模型精度過高造成的模型復(fù)雜度過高。
系數(shù)內(nèi)自省也
ARMA中的系數(shù),模型訓(xùn)練時(shí)會(huì)自動(dòng)擬合最優(yōu)參數(shù),平時(shí)用的時(shí)候不需要關(guān)心,但還是應(yīng)該知道大體是怎么來的。
AR(p)模型的參數(shù)估計(jì):
Yule-Walker估計(jì):用Levinson遞推公式解Y-W方程,能夠保證最小相位性,計(jì)算簡單。 最小二乘估計(jì):最小化殘差平方和,根據(jù)線性模型理論解正規(guī)方程,計(jì)算簡單。 最大似然估計(jì):聯(lián)合密度函數(shù)最大化,一般精度較高。
MA(q)模型的參數(shù)估計(jì):
矩估計(jì):利用參數(shù)與自協(xié)方差函數(shù)關(guān)系,用解非線性方程組的方法求解,誤差較大。 逆相關(guān)函數(shù)法:把MA變成一個(gè)AR再用Yule-Warker方法估計(jì)參數(shù)。 新息方法:計(jì)算樣本自協(xié)方差函數(shù),根據(jù)新息預(yù)報(bào)遞推公式計(jì)算參數(shù)。
ARMA(p,q)模型的參數(shù)估計(jì)
矩估計(jì)方法:用Yule-Walker方程估計(jì)AR模型參數(shù),然后可以用逆相關(guān)函數(shù)法估計(jì)MA模型參數(shù)。在中小樣本, 矩估計(jì)不是一種實(shí)用的方法, 即使作為最大似然估計(jì)的初值也不太合適。 自回歸逼近法:可以看成是回歸系數(shù),先擬合一個(gè)近似自回歸模型。然后算出殘差序列,對殘差平方和極小化最終得到估計(jì)參數(shù)。 最大似然估計(jì):也可以說是最小平方和估計(jì),平方和指的是誤差項(xiàng)。用最大似然估計(jì)可以大大改善MA部分的參數(shù)估計(jì)精度。
以上內(nèi)容參考自北大李東風(fēng)的應(yīng)用時(shí)間序列分析備課筆記:
https://www.math.pku.edu.cn/teachers/lidf/course/atsa/atsanotes/html/_atsanotes/atsa-estarma.html
短期預(yù)言家
ARMA模型適合短期預(yù)測,對于長期預(yù)測,預(yù)測結(jié)果偏向于均值,預(yù)測均方誤差趨于序列的方差。對于AR模型來說,預(yù)測得越遠(yuǎn),均方誤差越大;對于MA模型來說,到q步之后就沒了預(yù)測能力。
具體ARMA模型的預(yù)測公式是怎樣的,我們不妨一起看看AR模型和MA模型的預(yù)測。
AR模型的一步預(yù)測:
其中,為h+1時(shí)刻的誤差項(xiàng)未知。
所以超前一步的預(yù)測公式為:
預(yù)測誤差為:
AR模型的多步預(yù)測:
其中,
所以計(jì)算需要遞推計(jì)算。
超前k步的預(yù)測誤差為:
當(dāng)超前步數(shù)k趨近無窮大時(shí),趨近于序列均值,稱為均值回歸,和前一步的越強(qiáng)(越大),多步預(yù)報(bào)的效果也越差。
MA模型的一步預(yù)測:
根據(jù),
MA模型的多步預(yù)測:
其中,,即MA(2)中
因?yàn)镸A(q)序列在間隔超過q步以后就獨(dú)立,所以超前多步預(yù)測,只能預(yù)測到步,從q+1步開始就只能用均值預(yù)測了。
ARMA模型的一步預(yù)測:
ARMA模型的多步預(yù)測:?
其中,
;
輸入必要平穩(wěn)
序列平穩(wěn)是ARMA分析的前提,所以輸入序列必須是平穩(wěn)的。時(shí)間序列的平穩(wěn)性檢驗(yàn)主要有三種方法:
圖形分析方法:繪制時(shí)間序列的折線圖,看曲線是否穩(wěn)定;看自相關(guān)圖中自相關(guān)系數(shù)是否能很快退化到零。缺點(diǎn)是需要主觀判斷,沒有量化依據(jù)。 簡單統(tǒng)計(jì)方法:根據(jù)寬平穩(wěn)均值、方差不隨時(shí)間變化的特性,將序列前后拆分成兩段,分別計(jì)算均值、方差,對比看是否差異明顯。 假設(shè)檢驗(yàn)方法:當(dāng)前主流單位根檢驗(yàn),檢驗(yàn)序列中是否存在單位根,若存在,則為非平穩(wěn)序列,不存在則為平穩(wěn)序列。檢驗(yàn)方法有ADF檢驗(yàn)、PP檢驗(yàn)、KPSS檢驗(yàn)等。
具體實(shí)現(xiàn)可參考“時(shí)間序列的平穩(wěn)性檢驗(yàn)方法匯總篇”。
然事常與愿違,現(xiàn)實(shí)中的時(shí)間序列數(shù)據(jù)多是非平穩(wěn)的,檢驗(yàn)后發(fā)現(xiàn)非平穩(wěn)怎么辦,難道就不能使用ARMA了嗎?并不,事總在人為,可以先對序列進(jìn)行平穩(wěn)化處理。
常用平穩(wěn)化的方法有:
差分:差分可以去除序列中的趨勢和季節(jié)性。一階差分可以去除線性趨勢,如果還有二次趨勢,還可以繼續(xù)二階差分。二階差分后還未平穩(wěn)的話就要注意了,繼續(xù)差分即便最終平穩(wěn)了,但是多次差分后解釋力下降,且有可能造成過度差分,最差為差分后的序列為白噪聲,后面也沒法分析了。對于周期型序列也可以用季節(jié)差分的方式去除時(shí)間序列季節(jié)性。 平滑:對當(dāng)前序列值減去平滑值得到一個(gè)殘差序列,當(dāng)平滑結(jié)果能比較好的描述原始序列趨勢特征的時(shí)候,殘差序列一般是平穩(wěn)的,后續(xù)可對殘差序列進(jìn)行建模預(yù)測。計(jì)算平滑值的方法可以用簡單移動(dòng)平均、加權(quán)移動(dòng)平均、一次指數(shù)平滑、二次指數(shù)平滑等。同類思想,還可以擬合一個(gè)回歸方程,用回歸方程描述原始序列的趨勢特征。 變換:如對數(shù)變換,能夠去除方差隨時(shí)間增長的趨勢。對數(shù)據(jù)進(jìn)行取log處理,變換前的序列必須滿足大于0(小于0的話可以對序列用+x的方式變?yōu)檎龜?shù))。取對數(shù)后,原數(shù)據(jù)越大,縮小的幅度越大,可以使得方差隨時(shí)間波動(dòng)大的時(shí)間序列的方差變得更穩(wěn)定,從而一定程度上使得序列平穩(wěn)。但也不一定變換后即平穩(wěn),比如呈指數(shù)趨勢的序列,變換后只能將指數(shù)趨勢轉(zhuǎn)化為線性趨勢,此時(shí)再使用一階差分即可將序列變得平穩(wěn),同時(shí)變換后的數(shù)據(jù)可以看成增長率的對數(shù),解釋性強(qiáng)。其它還有開根號、Box-Cox變換、Yeo-Johonson變換等。這些變換試圖將數(shù)據(jù)轉(zhuǎn)換為正態(tài)分布,雖然對于平穩(wěn)性來說并不總是必要的,但通常能夠糾正序列的非線性問題。 分解:可以將時(shí)間序列分解成3部分:長期趨勢、季節(jié)變動(dòng)、不規(guī)則波動(dòng),3種成分相加叫加法模型,3種成分相乘叫乘法模型,1加1乘叫混合模型。分解目的為去除季節(jié)性的影響,分解后可對分解出的趨勢項(xiàng)、季節(jié)項(xiàng)和余項(xiàng)分別進(jìn)行預(yù)測。常用時(shí)間序列分解方法有樸素分解、X11分解、SEATS分解、STL分解等,其中STL分解用的較多。
平穩(wěn)化之后也莫急著訓(xùn)練模型,還需檢驗(yàn)序列是否白噪聲。因?yàn)榘自肼暿瞧椒€(wěn)的,但是卻是完全隨機(jī)的,沒法預(yù)測。所以如果序列是白噪聲的話,也就可以回家吃飯,莫要費(fèi)功夫鉆研了。
輸出還可再檢查
如果模型擬合充分,則殘差序列服從零均值正態(tài)分布且完全隨機(jī)無相關(guān)性。所以還需要分析殘差的正態(tài)性和無關(guān)性,以此檢驗(yàn)?zāi)P蛿M合是否良好。如果檢驗(yàn)未通過,說明模型不合適或者參數(shù)沒調(diào)好。
檢驗(yàn)殘差的正態(tài)性,可以查看殘差的正態(tài)概率圖、QQ圖,也可以使用normaltest正態(tài)性檢驗(yàn)等方法。
分布直方圖:以比較直觀的方式看數(shù)據(jù)分布是否服從正態(tài)分布。 QQ圖:Quantile-Quantile Plot,即分位數(shù)-分位數(shù)圖,QQ圖中若殘差基本完全落在45°線上即為符合正態(tài)性假設(shè)。 normaltest:scipy中normaltest根據(jù)數(shù)據(jù)的峰度偏度檢驗(yàn)是否符合正態(tài)分布,p值大于顯著性水平0.05認(rèn)為樣本數(shù)據(jù)符合正態(tài)分布,檢驗(yàn)較嚴(yán)格。
檢驗(yàn)殘差的無關(guān)性(白噪聲檢驗(yàn)),可以看殘差的自相關(guān)圖,也可以使用假設(shè)檢驗(yàn)方法D-W檢驗(yàn)、Box-Ljung檢驗(yàn)、Ljung-Box檢驗(yàn)。
自相關(guān)圖:白噪聲完全無自相關(guān)性,除0階自相關(guān)系數(shù)為1外,延遲k階的樣本自相關(guān)系數(shù)均為0或在0值附近。 D-W檢驗(yàn):杜賓-瓦特森檢驗(yàn),檢驗(yàn)序列是否存在一階自相關(guān)。DW值接近2時(shí)不存在一階自相關(guān)性。 Box-Ljung檢驗(yàn):原假設(shè)為滯后m階序列值之間相互獨(dú)立,即序列為獨(dú)立同分布的白噪聲,如果p值大于顯著性水平如0.05,不能拒絕原假設(shè),序列為白噪聲序列。 Ljung-Box檢驗(yàn):Box-Ljung檢驗(yàn)在小樣本量下不太精確,Ljung-Box檢驗(yàn)彌補(bǔ)了這一缺陷。同Box-Ljung檢驗(yàn),p值大于顯著性水平如0.05,不能拒絕原假設(shè),序列為白噪聲序列。
詳細(xì)白噪聲檢驗(yàn)方法可以看下“白噪聲檢驗(yàn)”。
放碼過來
讀取數(shù)據(jù)
使用statsmodels中自帶的美國夏威夷莫納羅亞天文臺(tái)大氣二氧化碳數(shù)據(jù),并轉(zhuǎn)換為月度數(shù)據(jù)。
import?numpy?as?np
import?pandas?as?pd
from?statsmodels.datasets?import?co2
from?statsmodels.tsa.stattools?import?adfuller
from?matplotlib?import?pyplot?as?plt
#?加載數(shù)據(jù)
data?=?co2.load(as_pandas=True).data
#?月度數(shù)據(jù)
data?=?data['co2']
data?=?data.resample('M').mean().ffill()
#?可視化
data.plot(figsize=(12,4))
plt.title('co2?data')
plt.show()
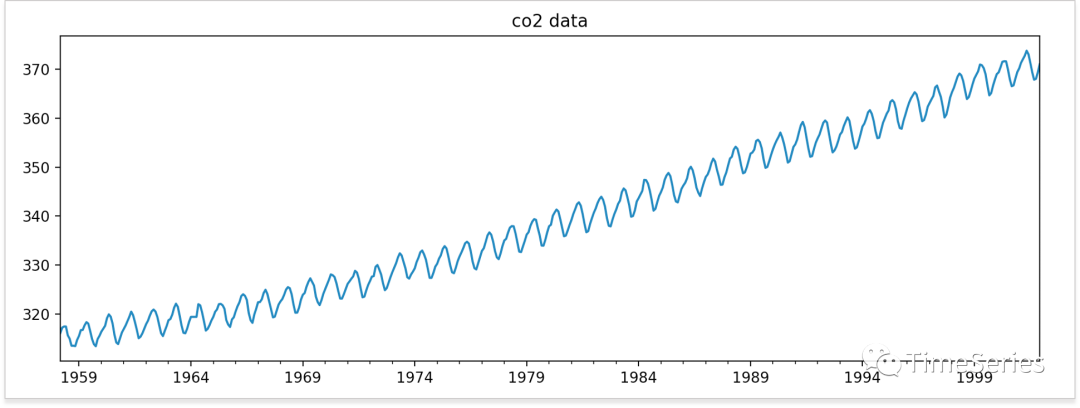
平穩(wěn)性檢驗(yàn)
能夠很直觀的看出來,存在趨勢和周期,必然非平穩(wěn),ADF檢驗(yàn)p值應(yīng)該很大。
res?=?adfuller(data)
print('p?value:',?res[1])
p value: 0.9989453312516823
p值顯著大于0.05,序列非平穩(wěn)。
平穩(wěn)化
先來使用差分的方式進(jìn)行平穩(wěn)化處理,因?yàn)橛兄芷谥苯邮褂眉竟?jié)差分。
#?#?一階差分
#?data_diff1?=?data.diff()
#?#?二階差分
#?data_diff2?=?data_diff1.diff()
#?季節(jié)差分
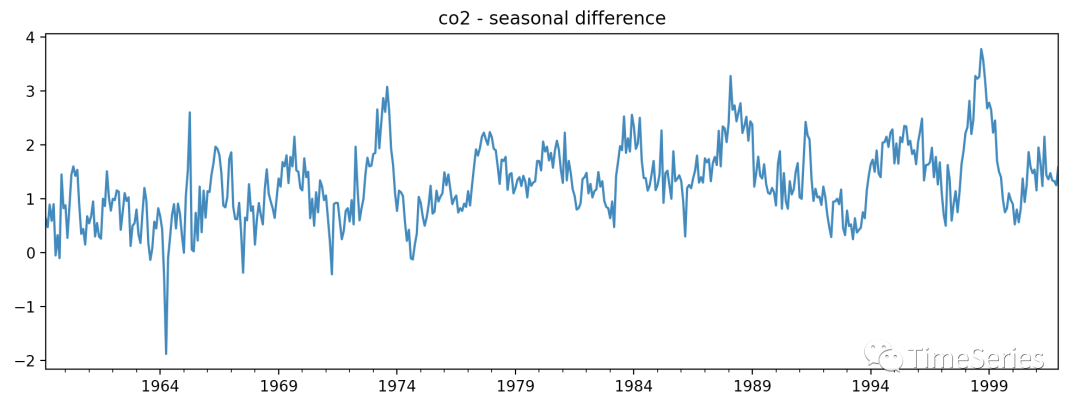
data_diff?=?data.diff(12).dropna()
data_diff.plot(figsize=(12,4))
plt.title('co2?-?seasonal?difference')
plt.show()
#?ADF檢驗(yàn)
res?=?adfuller(data_diff)
print('p?value:',?res[1])
季節(jié)差分后,ADF檢驗(yàn)中p值為0.0007小于0.05,故而差分后序列平穩(wěn)。
白噪聲檢驗(yàn)
檢驗(yàn)差分后的數(shù)據(jù)是否為白噪聲。
from?statsmodels.stats.diagnostic?import?acorr_ljungbox
res?=?acorr_ljungbox(data,?lags=[6,12,24],?return_df=True)
print(res)
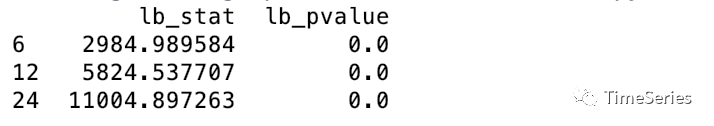
各滯后期數(shù)下p值都為0均小于0.05,差分后的序列非白噪聲,可以進(jìn)行預(yù)測。
模型定階
根據(jù)最小化BIC準(zhǔn)則確定p、q。計(jì)算比較耗時(shí),為了控制計(jì)算量,這里限制AR最大階不超過6,MA最大階不超過4。
from?statsmodels.tsa.stattools?import?arma_order_select_ic
bic_min_order?=?arma_order_select_ic(data_diff,?max_ar=6,?max_ma=4,?ic='bic')['bic_min_order']
print(bic_min_order)
求得ARMA的階數(shù)為(6,3)。
模型訓(xùn)練
from?statsmodels.tsa.arima_model?import?ARMA
model?=?ARMA(data_diff,?order=bic_min_order).fit(disp=-1)
print(model.summary())
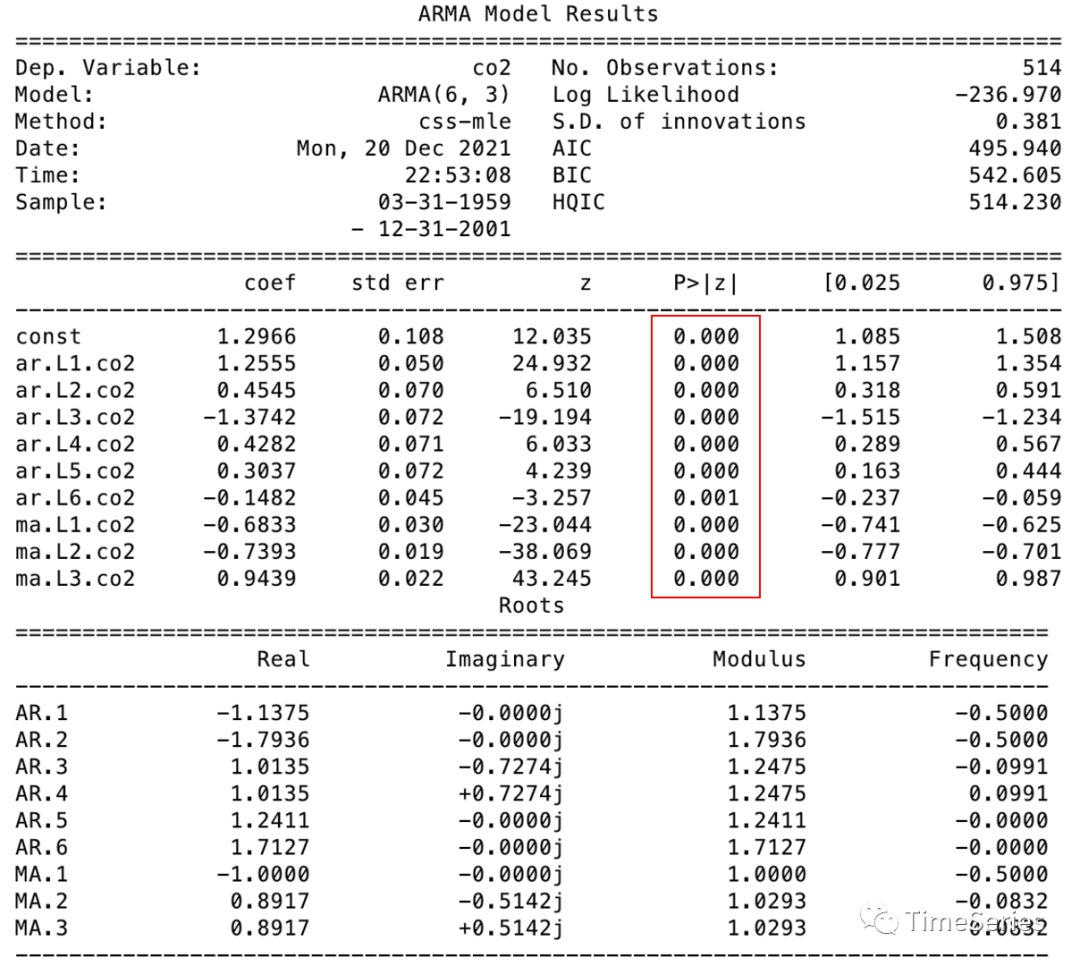
系數(shù)p值均小于0.05,說明系數(shù)均顯著不為0。如果存在某個(gè)系數(shù)的p值較大,說明t檢驗(yàn)中系數(shù)不顯著,貢獻(xiàn)不大,可以剔除,減小模型冗余度。
模型檢驗(yàn)
可視化殘差直方圖、QQ圖,看是否正態(tài)分布,可視化ACF看是否仍存有自相關(guān)性。
import?statsmodels.api?as?sm
from?statsmodels.graphics.tsaplots?import?plot_acf
fig,?axs?=?plt.subplots(2,?2)
fig.subplots_adjust(hspace=0.3)
model.resid.plot(ax=axs[0][0])
axs[0][0].set_title('residual')
model.resid.plot(kind='hist',?ax=axs[0][1])
axs[0][1].set_title('histogram')
sm.qqplot(model.resid,?line='45',?fit=True,?ax=axs[1][0])
axs[1][0].set_title('Normal?Q-Q')
plot_acf(model.resid,?ax=axs[1][1])
plt.show()
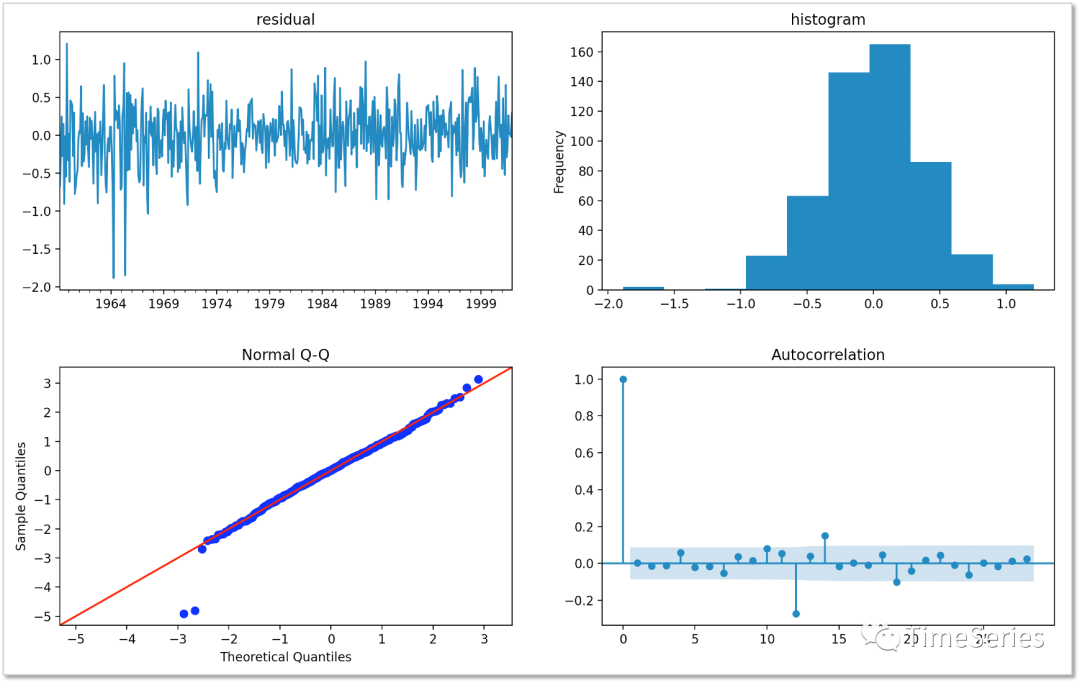
上圖可以看出殘差基本服從正態(tài)分布,但ACF圖顯示滯后12期時(shí)仍存在自相關(guān)性,所以模型還可優(yōu)化。猜想是否有可能模型定階時(shí)限制了AR和MA的最大階數(shù),所以直接根據(jù)差分后樣本數(shù)據(jù)的ACF圖和PACF圖定階。
from?statsmodels.graphics.tsaplots?import?plot_acf,?plot_pacf
fig,?axs?=?plt.subplots(2,?1)
plot_acf(data_diff,?ax=axs[0])
plot_pacf(data_diff,?ax=axs[1])
plt.show()
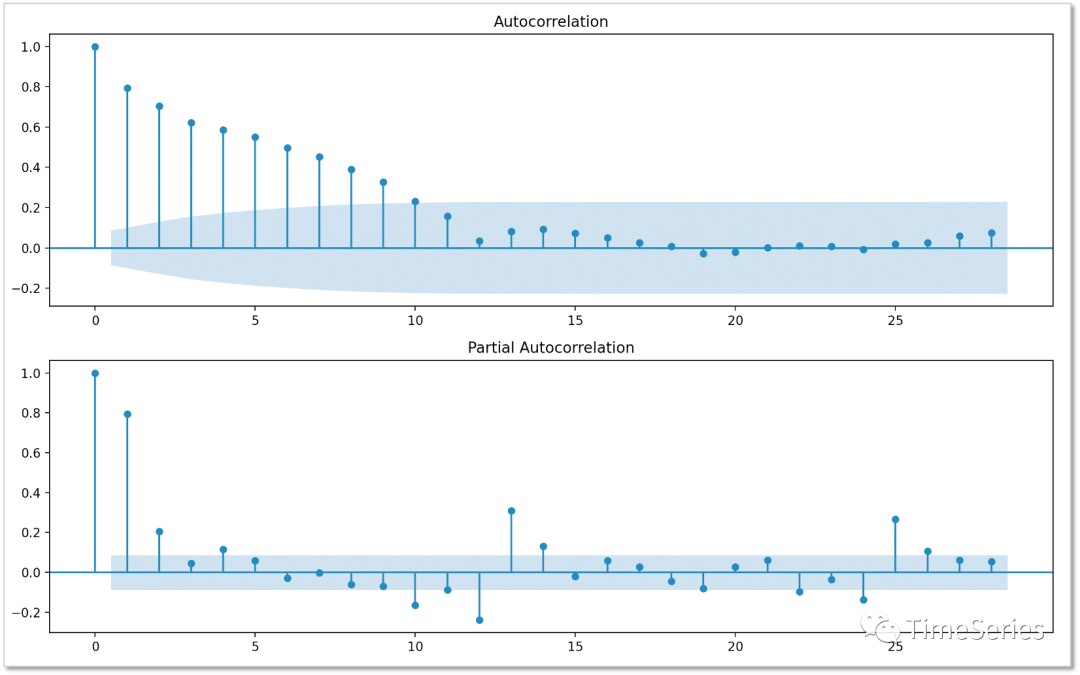
根據(jù)以上ACF、PACF圖,取p=2,q=11訓(xùn)練模型。
model2?=?ARMA(data_diff,?order=(2,11)).fit(disp=-1)
fig,?axs?=?plt.subplots(2,?2)
fig.subplots_adjust(hspace=0.3)
model.resid.plot(ax=axs[0][0])
axs[0][0].set_title('residual')
model.resid.plot(kind='hist',?ax=axs[0][1])
axs[0][1].set_title('histogram')
sm.qqplot(model.resid,?line='45',?fit=True,?ax=axs[1][0])
axs[1][0].set_title('Normal?Q-Q')
plot_acf(model.resid,?ax=axs[1][1])
plt.show()
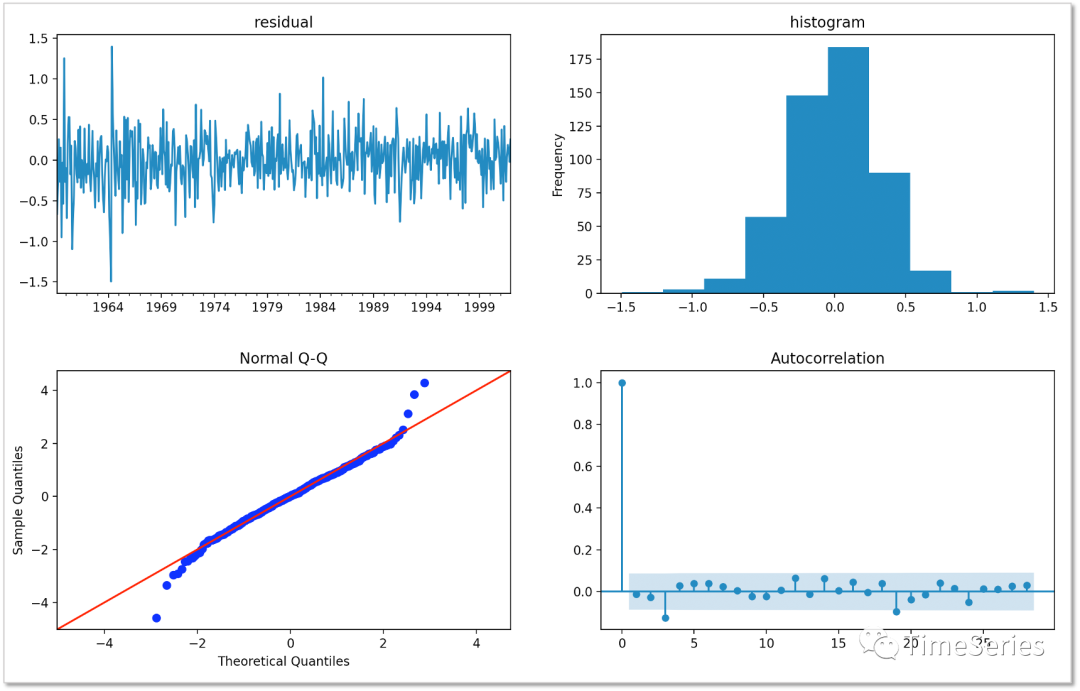
效果有所改善,符合預(yù)期。
模型預(yù)測
預(yù)測未來6期數(shù)據(jù)(注意ARMA模型預(yù)測時(shí),預(yù)測期數(shù)超過MA模型最大階數(shù)后,MA部分的預(yù)測值實(shí)際為序列均值不再變化,AR部分倒還會(huì)有持續(xù)變化但效果下降)。
preds?=?model.predict(0,?len(data_diff)+6)
#?也可只取未來預(yù)測值
#?fcast?=?model2.forecast(6)
plt.figure(figsize=(12,?4))
data_diff.plot(color='g',?label='data_diff')
preds.plot(color='r',?label='predict')
plt.legend()
plt.show()
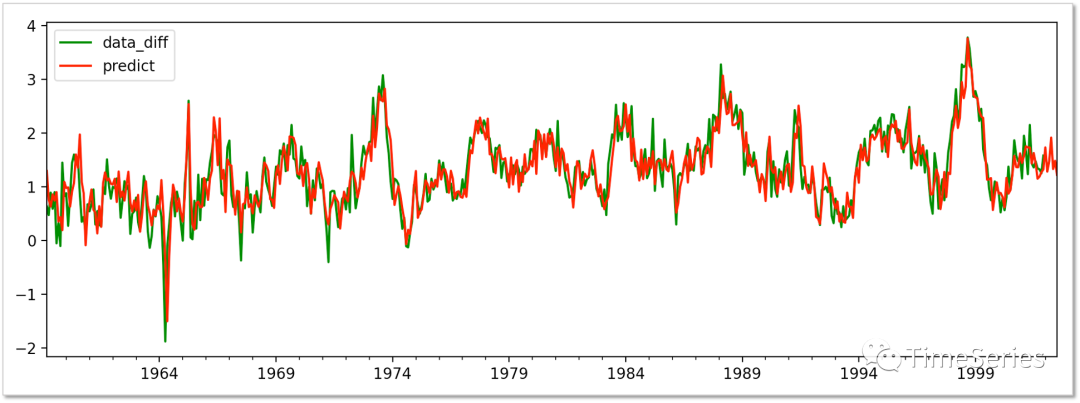
差分還原
把曾經(jīng)減去的項(xiàng)再加回來。
df1?=?pd.DataFrame(data)
df2?=?pd.DataFrame(preds,?columns=['predict'])
df?=?pd.concat([df1,?df2],?axis=1)
df['result']?=?df['predict']?+?df['co2'].shift(12)
plt.figure(figsize=(12,?4))
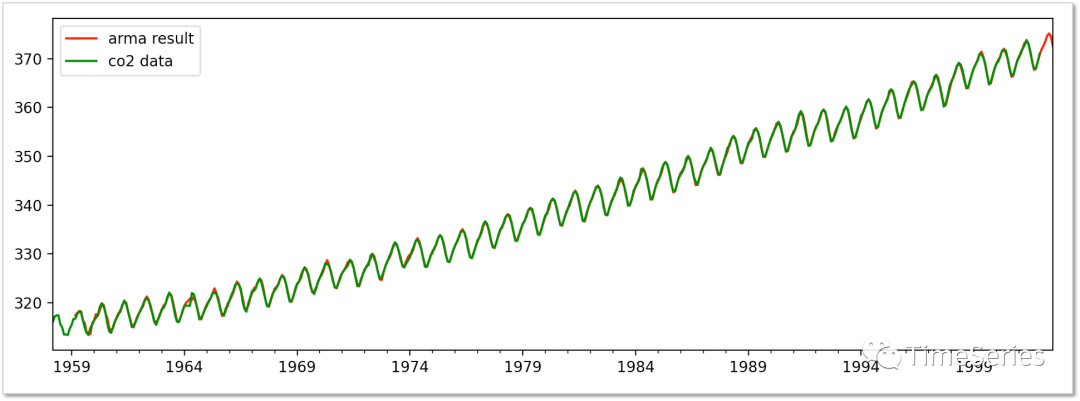
df['result'].plot(color='r',?label='arma?result')
df['co2'].plot(color='g',?label='co2?data')
plt.legend()
plt.show()