0.00...1是個什么數(shù)？

數(shù)學算法俱樂部

日期：2020年09月18日

正文共：4056字0圖

預計閱讀時間：11分鐘

來源：搜狐網(wǎng)

某些人仍然根據(jù)有限小數(shù)的經(jīng)驗，認為，0.99...不等于1。他們認為，0.99...雖然是無限小數(shù)，但是有最后一位，就是在無窮遠處的那一位，因此0.9循環(huán)可以寫成0.99...9，顯然它與1差了0.00...1，小數(shù)點后無窮個0，最后跟了個1。

這種關于無限小數(shù)的想法當然是錯誤的。回憶一下在實數(shù)系中引進無限循環(huán)小數(shù)的目的和依據(jù)：有理數(shù)在實數(shù)中稠密(即處處都有，任何一個小區(qū)間里都有有理數(shù))，又在有理數(shù)中稠密，因此它在實數(shù)集中也稠密。因此我們可以用一個m/10^n形式有理數(shù)的數(shù)列去逼近任何的實數(shù)。因此我們的無限小數(shù)作為{m /10^n}數(shù)列的完成式，在小數(shù)點后面跟著的就是個由0-9數(shù)字組成的數(shù)列，它的每一項都跟自然數(shù)有一一對應的關系，而自然數(shù)根本就沒有最后一項。可見，0.99...是無法寫成0.99...9的。

那么，0.00...1是個什么數(shù)？

首先指出，它既不是有限小數(shù)，也不是我們平常所見的無限小數(shù)，因此它根本不是一個實數(shù)。

它不是個有限小數(shù)，這是顯然的，因為小數(shù)點后面有無窮個0。那它為什么不是無限小數(shù)呢？前面已經(jīng)說過，任何一個無限小數(shù)，后面的小數(shù)位按從左到右的順序與自然數(shù)一一對應，任何一個小數(shù)位都對應一個有限的自然數(shù)。反觀0.0...1，最后的那個1，不對應任何有限的自然數(shù)，前面的無限多個0就已經(jīng)把所有自然數(shù)都對應完了。從小數(shù)運算規(guī)律來看的話，如果要把0.0...1與0.99...相加，那么0.99...中所有的9都與0.0...1中的0對應相加，0.0...1最后的那個1要加在哪一位呢？如果按無限小數(shù)對應實數(shù)的規(guī)則把它放在實數(shù)軸上，它要放在哪里呢？它非負，又小于所有形如 1/10^n的數(shù)，這樣的數(shù)只有0。因此前面的無限多個0就已經(jīng)決定了它只能是0了，后面的1對它的值來講沒有意義，沒有存在的必要。

雖然在實數(shù)的范圍內(nèi)它是沒有必要存在的表達式，但我們依然有必要從形式上討論它，因為現(xiàn)在的數(shù)系發(fā)展早已經(jīng)超越了實數(shù)，從一維的實數(shù)擴展到高維的復數(shù)、四元數(shù)等；從標準的實數(shù)擴展到了非標準的超實數(shù)、廣義實數(shù)等。所以數(shù)的范圍在擴大，概念并不唯一。在其它數(shù)系中是否可能有它的身影呢？我們最好先看看這個數(shù)的特征。

因為小數(shù)點后面的0的個數(shù)已經(jīng)是無限的了，這些0占滿了所有以自然數(shù)為標號的小數(shù)位，然后在這些無窮多個0后面緊接著又出現(xiàn)了一個1，已經(jīng)超出了以自然數(shù)為下標的數(shù)列的研究范圍。對于這個形式上的“數(shù)”，僅有自然數(shù)的知識就不夠了，需要把自然數(shù)向無窮情形做一種推廣。回想上一節(jié)的無窮基數(shù)的理論，它就是從“ 個數(shù)”角度把自然數(shù)推廣到了無窮的情形，但對于我們的問題，光是討論小數(shù)位的個數(shù)是不行的，因為我們說過，在可數(shù)無窮多個元素基礎上增加一個元素，元素個數(shù)沒什么改變，仍然是可數(shù)無窮，你很容易把最后添加的那個1對應自然數(shù)的第一個元素，然后把原來的每個對應位都向后移動一位，所有元素仍然是一一對應于自然數(shù)集的。

但是注意到，一旦把一個小數(shù)的數(shù)位順序打亂，它的值就變了，它必須保持原來的順序。因此我們需要一些無窮序數(shù)的知識，它是自然數(shù)向無窮世界的另一種推廣。

一般而言，序數(shù)是用來表示有序序列中位置的數(shù)，量數(shù)（或叫基數(shù)）是用來表示“有多少數(shù)量”的數(shù)。

序數(shù)對應于排列，如在以下句子中的“一”及“二”：“這人一不會打字，二不懂速記，所以不可以做秘書。”量數(shù)對應于量詞，例如在以下句子中的“一”及“四”：“有一個橙，有四個柑。”

有關序數(shù)的定義，你可以查閱ｗｉｋｉ百科“序數(shù)”詞條。但那些形式化的定義對初學者來說都太抽象。我們可以先看一下序數(shù)的樣子。首先需要知道“良序集”的概念：
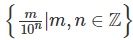
在一個集合A上定義一個二元關系“≤”，如果滿足：

①對每個x∈A，有x≤x(自反性)。②若x≤y與y≤x則x＝y(tǒng)(反對稱性)。③若x≤y,y≤z則x≤z(傳遞性)。④對任何x∈A，y∈A，x≤y或y≤x中必有一成立，則稱"≤"為A上的全序關系，稱A在“≤”關系下為全序集，簡記為(A,≤)。

自然數(shù)集、實數(shù)集在數(shù)的“小于等于”關系下都是全序集，數(shù)的“小于等于”關系就是這些集合上的全序關系。對于集合{{1,2,3},{1}, {2}}，包含關系“?”就不是全序關系，因為包含關系雖然滿足上述的前三條，但在這個特殊集合上它不滿足第四條，{1}和{2}就沒有誰包含誰的關系。

如果一個全序集(A,≤)，它的任何非空子集都有最小元素，則稱≤為良序關系，A在“≤”下為良序集。自然數(shù)就是一個典型的良序集，實數(shù)集在數(shù)的大小意義下就不是良序集，不存在大于0的最小元素。

從直觀上看一個良序集是什么樣子呢？
首先，因為是良序，那么A中有唯一一個最小元素，記為a0，去掉a0之后還有一個最小元素，記為a1，依此類推，可得一列元素an，使得

a0≤a1≤a2≤a3≤...

因為an各不相同，所以可以按照通常的習慣把所有的"≤"改成"<"。任何不在這個序列中的元素（如果有的話）都比這列元素中的任何一個大。從A中去掉所有的an，如果還能得到一個非空子集的話，那么這個子集中還有最小元素。剛才標記an序列的時候所有的自然數(shù)都用上了，那么這個元素就賦于一個新的標號：記為aω，依此類推，又得到一列元素a(ω+n)，所以現(xiàn)在A中的前面一部分元素在"<"的順序下排成這個形狀：

其中三點的省略號代表有限個元素，六點的省略號代表無限個元素。an和aω之間有無窮個自然數(shù)標號元，a(ω+n)和a(ω*2)之間有無窮多個(ω+自然數(shù))標號的元素，a(ω*n)與a(ω^2)之間有無窮個標號為形如(ω*k+r)(k,r都為自然數(shù))的元素......

這里的元素下標就是序數(shù)。序數(shù)，就是標定良序集中元素順序的標號，是自然數(shù)的一種推廣。初步的，我們得到最前面一些序數(shù)的形狀：

但是，這樣的描述缺乏數(shù)學上的嚴謹性，總不能把一個數(shù)學上的序數(shù)概念定義為“如上所示的一列數(shù)”吧？另外，上面的一列數(shù)有什么性質(zhì)？是否有一個最大元？是否每一個良序集都可以用序數(shù)給每一個元素標號？這些問題都有待嚴格定義序數(shù)。

序數(shù)的一個直觀且嚴謹?shù)亩x是用歸納法定義的，它完全是序數(shù)生成過程的描述：

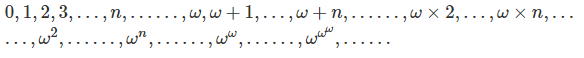
1) 空集 ? 是序數(shù)；
2) 如果a是序數(shù)，則a的后繼 a∪{a} 也是序數(shù)；
3) 如果A是由序數(shù)構成的集合，那么A中所有元素的并集也是序數(shù)；
4) 所有的序數(shù)都由上述三條界定。
由上面的定義，我們可以寫出開頭的一些序數(shù)如下：
?,?∪{?}={?},{?}∪{{?}}={?,{?}},{?,{?},{?,{?}}},...
將開頭的這些有限序數(shù)分別簡記為1,2,3,4,...,n,它們就是自然數(shù)在集合論中的定義。由此可見，
0=?,1={?}={0},2={?,{?}}={0,1},3={?,{?},{?,{?}}}={0,1,2}...n={0,1,2,...,n-1},n+1=n∪{n}={1,2,3,...,n}。

這些自然數(shù)有一個共同的特點：都是由空集通過定義中的第二條生成的，每一個都既屬于后一個，又包含于后一個。所有的自然數(shù)可以構成集合，這是公理集合論的假設。因此，根據(jù)序數(shù)的定義條款3)，所有自然數(shù)的并集(記為ω)也是序數(shù)。那么所有自然數(shù)的并集是什么呢？

注意到任何一個自然數(shù)n，n是n+1的元素，因此n∈ω，反過來任意ω中的元素都屬于某個自然數(shù)，而自然數(shù)的元素也是自然數(shù)，所以ω就是自然數(shù)集本身。反復應用上面的定義，就可以得到類似于上面的那一長串序數(shù)。由序數(shù)的定義，還可以有超限歸納法，并證明，對于任何一個序數(shù)集，包含關系"?"是一個良序關系，并且∈是?的嚴格序關系，既 a∈b等價于a?b且a≠b。

下面證明：任何一個良序集都可以用序數(shù)為元素按順序標號。設X是良序集，用0標記最小元，1標記第二小的元素，...，假設無法用序數(shù)為X中所有元素標號，那么能夠獲得標號的元素和無法獲得標號的元素分別組成X的兩個子集，分別記為Y和 Z，Y中的元素都比Z中的小。若Y中有最大元，標號為a，那么為Z中最小元標號a∪{a}，由定義，它也是序數(shù)，大于所有Y中的標號，矛盾；若Y中無最大元，那么Y中所有元素標號構成集合，此為序數(shù)構成的集合，所有序數(shù)之并集也是序數(shù)，這個序數(shù)未出現(xiàn)在Y的標號中，（因為假設它是Y某元素的標號，Y中無最大元，那么Y中總能找到比這個序數(shù)大的標號，即真包含這個序數(shù)的標號，矛盾）把Z中最小元素標記為此序數(shù)，也與假設矛盾。

至于是否有不可數(shù)無窮個序數(shù)，是否每個集合都能夠定義良序關系，這里不去探討了，可以參看公理集論的內(nèi)容。

有了序數(shù)的概念，那么0.00...1的問題就有了理論依據(jù)：前面的0對應的標號都是自然數(shù)，最后的那個1對應第一個無窮序數(shù)ω。那么，我們看到，它確實跟0.99...不是一類數(shù)，暫且叫它“超級無窮小數(shù)”吧。

以下設x=0.00...1

▋第一個問題：0.00...1*10=?

根據(jù)有限小數(shù)的經(jīng)驗，一個小數(shù)乘以10，既可以理解為小數(shù)點向右移動一位，也可以理解為所有數(shù)位向左串一位。對于第一種理解，小數(shù)點向右移動一位，前面的0 還是無窮個，仍然可以占滿所有自然數(shù)標號，因此有x*10=x。對于第二種理解，所有數(shù)位向左串一位，前面無窮個0的標號都減1，第0個標號移到了整數(shù)位，這沒有問題。但最后的那個標號為ω的，卻有問題：在序數(shù)中，不存在ω的前一個和ω緊臨的序數(shù)，它向前移動一位，立刻跌進了深淵，消失在自然數(shù)尾部那個無窮的迷霧中了，因此可以有x*10=0.000...=0。

▋第二個問題：0.00...1/10=?

根據(jù)有限小數(shù)的經(jīng)驗，一個小數(shù)除以10，既可以理解為小數(shù)點向左移動一位，也可以理解為所有數(shù)位向右串一位。對于第一種理解，有x/10=x，對于第二種理解，x/10=0.00...01，注意0.00...01這個數(shù)最后的0和1分別對應ω和ω+1。

這是假定超級無限小數(shù)的數(shù)的位置是按前后順序排成良序集，從而根據(jù)有限小數(shù)的經(jīng)驗推得的幾種可能情況。但是可以看到，孤立地研究單獨的一個數(shù)，可以有很多種可能，如果不把它放在具體的數(shù)系中，這種研究是沒有什么意義的。

—?THE END —

?圖論的各種基本算法

?82歲江澤民在2008年發(fā)表論文指出：發(fā)展智能化，機器學習將有所作為……

?數(shù)學的關鍵是思想

?機器學習中需要了解的 5 種采樣方法

?北大讀博手記：怎樣完成自己的博士生涯？非常具有指導性！

?數(shù)學傳奇——代數(shù)幾何的白馬王子肖剛