太強了，手擼一款導(dǎo)彈跟蹤算法（Python版）

作者：半壺砂  

https://www.cnblogs.com/halfsand/p/7976636.html

這里涉及攔截導(dǎo)彈的自動跟蹤。最近，看到了一個挺有趣的自動跟蹤算法，一個Python的簡單模擬版本，分享給大家。

自動追蹤算法，在我們設(shè)計2D射擊類游戲時經(jīng)常會用到，這個聽起來很高大上的東西，其實也并不是軍事學的專利，在數(shù)學上解決的話需要去解微分方程。

這個沒有點數(shù)學基礎(chǔ)是很難算出來的。但是我們有了計算機就不一樣了，依靠計算機極快速的運算速度，我們利用微分的思想，加上一點簡單的三角學知識，就可以實現(xiàn)它。

好，話不多說，我們來看看它的算法原理，看圖：

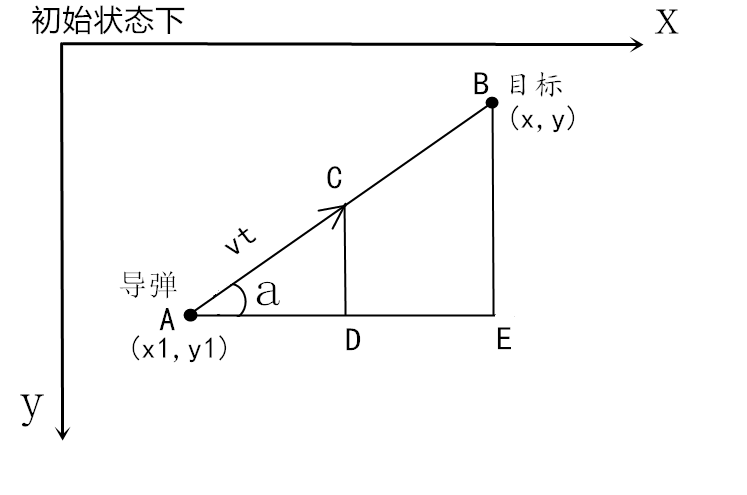
由于待會要用pygame演示，他的坐標系是y軸向下，所以這里我們也用y向下的坐標系。

算法總的思想就是根據(jù)上圖，把時間t分割成足夠小的片段（比如1/1000，這個時間片越小越精確），每一個片段分別構(gòu)造如上三角形，計算出導(dǎo)彈下一個時間片走的方向（即∠a）和走的路程（即vt=|AC|），這時候目標再在第二個時間片移動了位置，這時剛才計算的C點又變成了第二個時間片的初始點，這時再在第二個時間片上在C點和新的目標點構(gòu)造三角形計算新的vt，然后進入第三個時間片，如此反復(fù)即可。

假定導(dǎo)彈和目標的初始狀態(tài)下坐標分別是(x1,y1),(x,y)，構(gòu)造出直角三角形ABE，這個三角形用來求∠a的正弦和余弦值，因為vt是自己設(shè)置的，我們需要計算A到C點x和y坐標分別移動了多少，移動的值就是AD和CD的長度，這兩個分別用vt乘cosa和sina即可。

計算sina和cosa，正弦對比斜，余弦鄰比斜，斜邊可以利用兩點距離公式計算出，即：

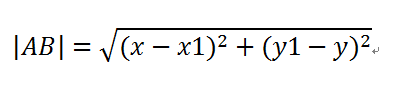
于是

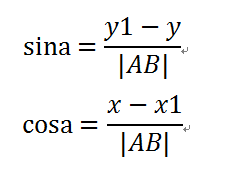
AC的長度就是導(dǎo)彈的速度乘以時間即  |AC|=vt，然后即可計算出AD和CD的長度，于是這一個時間片過去后，導(dǎo)彈應(yīng)該出現(xiàn)在新的位置C點，他的坐標就是老的點A的x增加AD和y減去CD。

于是，新的C點坐標就是：

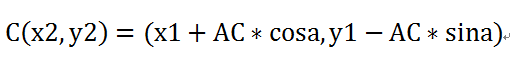
只要一直反復(fù)循環(huán)執(zhí)行這個操作即可，好吧，為了更形象，把第一個時間片和第二個時間片放在一起看看：

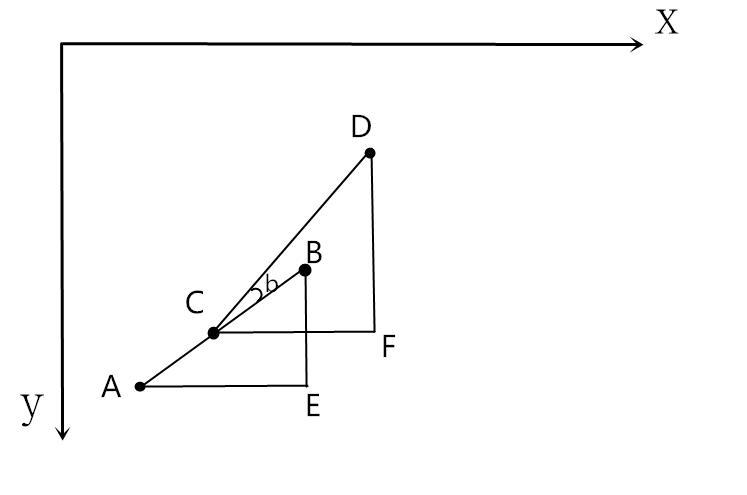
第一個是時間片構(gòu)造出的三角形是ABE，經(jīng)過一個時間片后，目標從B點走到了D點，導(dǎo)彈此時在C點，于是構(gòu)造新的三角形CDF，重復(fù)剛才的計算過程即可。

圖中的角∠b就是導(dǎo)彈需要旋轉(zhuǎn)的角度,現(xiàn)實中只需要每個時間片修正導(dǎo)彈的方向就可以了，具體怎么讓導(dǎo)彈改變方向，這就不是我們需要研究的問題了。

好，由于最近在用Python的pygame庫制作小游戲玩，接下來我們就用pygame來演示一下這個效果，效果如下圖：

很簡單的代碼如下：

import pygame,sys
from math import *
pygame.init()
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/red_pointer.png').convert_alpha()
x1,y1=100,600           #導(dǎo)彈的初始發(fā)射位置
velocity=800            #導(dǎo)彈速度
time=1/1000             #每個時間片的長度
clock=pygame.time.Clock()
old_angle=0
while True:
    for event in pygame.event.get():
        if event.type==pygame.QUIT:
            sys.exit()
    clock.tick(300)
    x,y=pygame.mouse.get_pos()          #獲取鼠標位置，鼠標就是需要打擊的目標
    distance=sqrt(pow(x1-x,2)+pow(y1-y,2))      #兩點距離公式
    section=velocity*time               #每個時間片需要移動的距離
    sina=(y1-y)/distance
    cosa=(x-x1)/distance
    angle=atan2(y-y1,x-x1)              #兩點線段的弧度值
    x1,y1=(x1+section*cosa,y1-section*sina)
    d_angle = degrees(angle)        #弧度轉(zhuǎn)角度
    screen.blit(missile, (x1-missile.get_width(), y1-missile.get_height()/2))
    dis_angle=d_angle-old_angle          #dis_angle就是到下一個位置需要改變的角度
    old_angle=d_angle                    #更新初始角度
    pygame.display.update()

如果僅把導(dǎo)彈考慮為一個質(zhì)點的話，那么以上算法就已經(jīng)足矣，我沒有做導(dǎo)彈的旋轉(zhuǎn)，因為一個質(zhì)點也不分頭尾不需要旋轉(zhuǎn)，當然這前提得是你加載的導(dǎo)彈圖片很小的時候不旋轉(zhuǎn)看起來也沒什么問題。

但是在pygame里面做旋轉(zhuǎn)并不是一件容易的事情(也可能是我無知)，好吧我們先把圖片替換成一張矩形的，再加入旋轉(zhuǎn)函數(shù)看看效果如何。

missiled = pygame.transform.rotate(missile, -(d_angle))
screen.blit(missiled, (x1-missile.get_width(), y1-missile.get_height()/2))

因為圖片的坐標點是它的左上角的點，所以如果我們想讓圖片的坐標固定在箭頭尖點，那么把圖片實際打印位置x減少圖片長度，y減少一半寬度就行。

但是實際運行效果并不好：

大致方向相同，但是圖片箭頭的尖點并沒有一直跟隨鼠標，這是為什么呢。經(jīng)過我的研究（就因為這個問題沒解決一直沒發(fā)布），

我發(fā)現(xiàn)原來是這個圖旋轉(zhuǎn)的機制問題，我們看看旋轉(zhuǎn)后的圖片變成什么樣了：

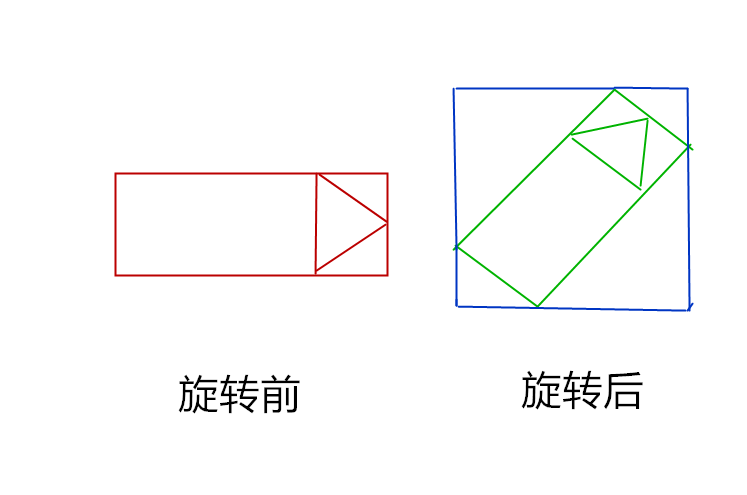
旋轉(zhuǎn)后的圖片變成了藍色的那個范圍，根據(jù)旋轉(zhuǎn)角度的不同，所變成的圖片大小也不一樣，我們看旋轉(zhuǎn)90的情況：

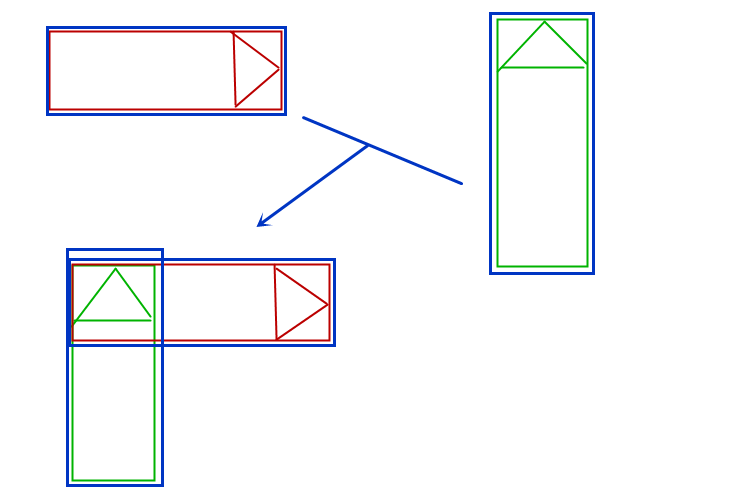
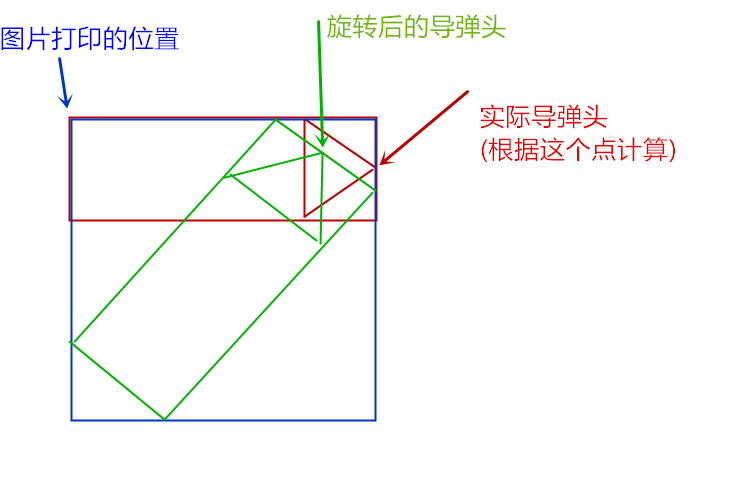
我們發(fā)現(xiàn)，旋轉(zhuǎn)后的圖片不僅面積變大了，導(dǎo)彈頭的位置也變了。那應(yīng)該怎么解決這個問題呢？思路是，每一次旋轉(zhuǎn)圖片以后，求出旋轉(zhuǎn)圖的頭位置（圖中的綠色箭頭點），然后把綠圖的打印位置移動一下，下，x，y分別移動兩個頭的距離，就可以讓旋轉(zhuǎn)后的導(dǎo)彈頭對準實際我們參與運算的那個導(dǎo)彈頭的位置，移動后應(yīng)該是這樣的：

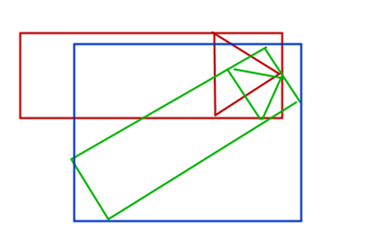
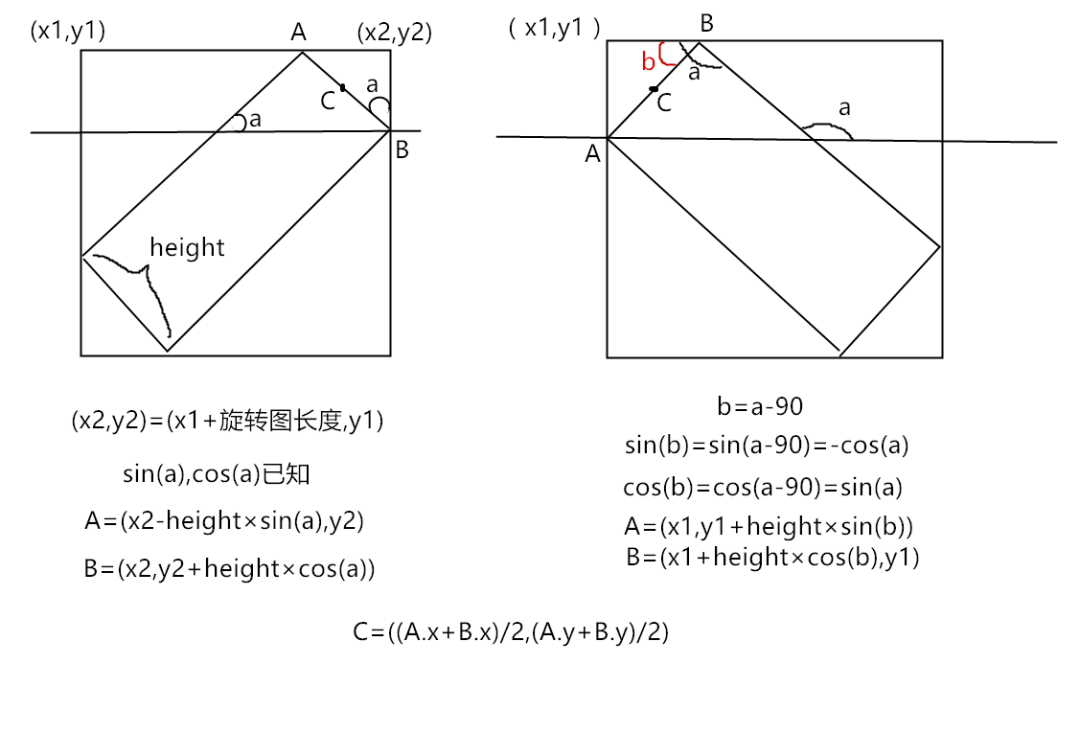
這樣，兩個導(dǎo)彈頭的點就一致了。接下來我們分析求旋轉(zhuǎn)后的導(dǎo)彈頭的算法。根據(jù)旋轉(zhuǎn)角度的不同，旋轉(zhuǎn)角在不同象限參數(shù)不一樣，所以我們分為這四種情況

1，2象限：

3，4象限，它的旋轉(zhuǎn)只有正負0—180，所以3，4象限就是負角。

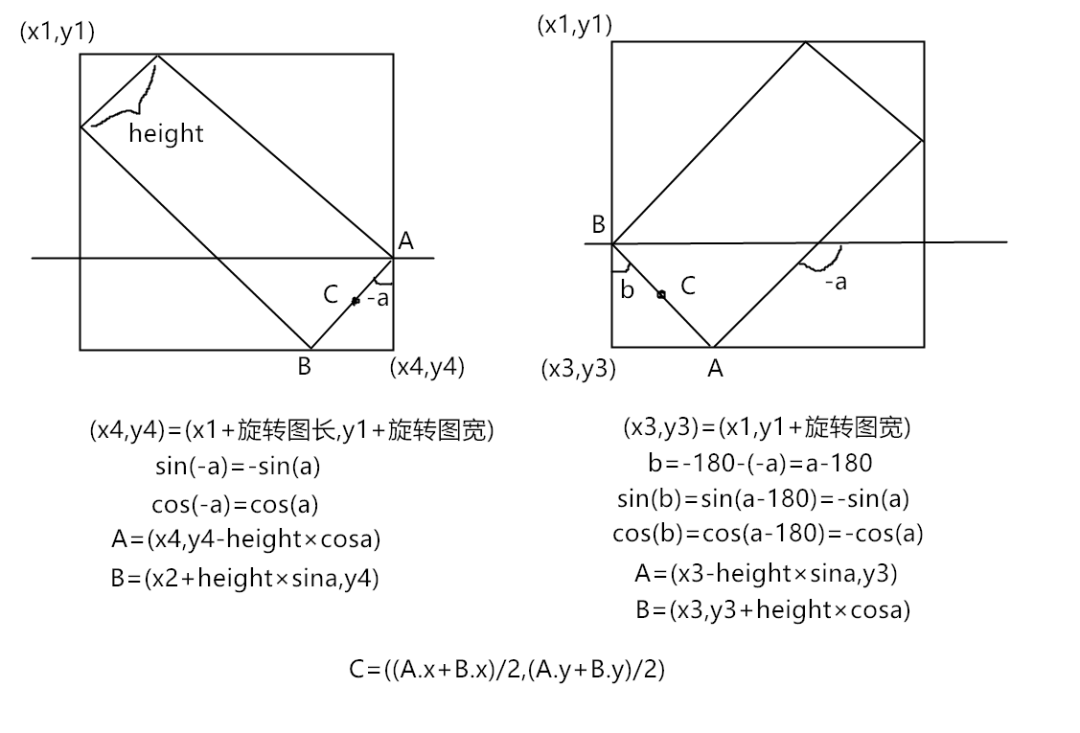
顯示圖片的時候我們將他移動。

screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))

這里的（x1-width,y1-height/2）其實才是上圖中的（x1,y1）。

所以最后我們加入相關(guān)算法代碼，效果就比較完美了。

大功告成，最后附上全部的算法代碼：

import pygame,sys
from math import *
pygame.init()
font1=pygame.font.SysFont('microsoftyaheimicrosoftyaheiui',23)
textc=font1.render('*',True,(250,0,0))
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/rect1.png').convert_alpha()
height=missile.get_height()
width=missile.get_width()
pygame.mouse.set_visible(0)
x1,y1=100,600           #導(dǎo)彈的初始發(fā)射位置
velocity=800            #導(dǎo)彈速度
time=1/1000             #每個時間片的長度
clock=pygame.time.Clock()
A=()
B=()
C=()
while True:
    for event in pygame.event.get():
        if event.type==pygame.QUIT:
            sys.exit()
    clock.tick(300)
    x,y=pygame.mouse.get_pos()          #獲取鼠標位置，鼠標就是需要打擊的目標
    distance=sqrt(pow(x1-x,2)+pow(y1-y,2))      #兩點距離公式
    section=velocity*time               #每個時間片需要移動的距離
    sina=(y1-y)/distance
    cosa=(x-x1)/distance
    angle=atan2(y-y1,x-x1)              #兩點間線段的弧度值
    fangle=degrees(angle)               #弧度轉(zhuǎn)角度
    x1,y1=(x1+section*cosa,y1-section*sina)
    missiled=pygame.transform.rotate(missile,-(fangle))
    if 0<=-fangle<=90:
        A=(width*cosa+x1-width,y1-height/2)
        B=(A[0]+height*sina,A[1]+height*cosa)

    if 90<-fangle<=180:
        A = (x1 - width, y1 - height/2+height*(-cosa))
        B = (x1 - width+height*sina, y1 - height/2)

    if -90<=-fangle<0:
        A = (x1 - width+missiled.get_width(), y1 - height/2+missiled.get_height()-height*cosa)
        B = (A[0]+height*sina, y1 - height/2+missiled.get_height())

    if -180<-fangle<-90:
        A = (x1-width-height*sina, y1 - height/2+missiled.get_height())
        B = (x1 - width,A[1]+height*cosa )

    C = ((A[0] + B[0]) / 2, (A[1] + B[1]) / 2)

    screen.fill((0,0,0))
    screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))
    screen.blit(textc, (x,y)) #鼠標用一個紅色*代替
    pygame.display.update()

最后

這是一個簡單的，用 Python 實現(xiàn)的自動跟蹤算法，真正的導(dǎo)彈攔截跟蹤算法要復(fù)雜很多。