華人學者彭泱獲頂會最佳論文獎:最快求解雞兔同籠問題?靠“猜”

大數(shù)據文摘授權轉載自AI科技評論
作者:陳彩嫻、青暮
在大多數(shù)同學的記憶里,數(shù)學老師也許都說過這么一句話:“問題的答案不能靠猜!”
但是,近日,來自佐治亞理工學院的華人學者彭泱(Richard Peng)卻憑借“迭代猜測”策略,提出了一種能夠更快求解線性方程組的方法,并因此獲得 2021 年算法頂會 ACM-SIAM 的最佳論文獎!
線性方程組是數(shù)學領域的奠基計算命題之一。去年 7 月,彭泱及其合作伙伴 Santosh Vempala 將一種求解線性方程組的新方法發(fā)表于 arXiv 上,今年 1 月在 ACM-SIAM 離散算法專題研討會(ACM-SIAM Symposium on Discrete Algorithms,簡稱“SODA”)上展示,獲得同行的一致肯定。
自1990年來,SODA每年舉辦一次,舉辦時間通常在一月份。該會議由ACM算法和計算理論特別興趣小組(SIGACT)和SIAM離散數(shù)學活動小組共同贊助,其形式更像是理論計算機科學會議,而不是數(shù)學會議,是算法研究的頂級會議之一。2021 年,SODA 所收到的論文投稿為 637 篇,接收文章總量為 180 篇。
那么,彭泱是誰?

彭泱出生于江蘇南京,2000 年隨家人移民至加拿大。計算機與數(shù)學天賦極佳,八年級時參加十年級水平的美國數(shù)學比賽獲得滿分成績,2004年與2005年獲得加拿大計算機比賽金牌,2005年在第46屆國際奧林匹克數(shù)學比賽中摘獲銀牌,同年在第17屆國際奧林匹克信息學比賽中獲得金牌。
高中畢業(yè)后,他繼續(xù)在數(shù)學與計算機的學習上保持優(yōu)異成績:
2006年至2009年在加拿大滑鐵盧大學攻讀數(shù)學學士學位,隨后直博到卡內基梅隆大學攻讀 CS 博士學位,師從 Gary L. Miller 教授(首次提出基于廣義黎曼猜想的確定性算法),期間獲得 2011 年微軟研究博士獎學金,其博士論文“Algorithm Design using Spectral Graph Theory”獲得 CMU SCS 杰出論文獎。
隨后,2013年至2015年,他又在麻省理工學院數(shù)學系擔任博士后研究員,師從 Jonathan A. Kelner 教授。
2015年8月,彭泱加盟佐治亞理工學院計算機科學學院擔任助理教授,2019年2月獲得 NSF 教職獎。2016年至2018年期間曾在上海財經大學擔任訪問教授。他的研究興趣主要是高效算法的設計、分析與執(zhí)行。
在好友蔣炎巖(南京大學CS博士,獲得2019年 CCF 優(yōu)秀博士學位論文獎)的眼里,彭泱“是個非常神奇的人物:記憶力超強、解題速度超快、受到的訓練超好。”
在接受 QuantaMagazine 的采訪中,彭泱表示:“(在這個思路里),你可以猜測求解的過程,且沒有老師會為此責備你。”
研究背景
線性方程組是計算領域最基本的問題之一。線性方程組一般包含兩個或多個帶有變量的方程式。這些變量表示事物之間相互聯(lián)系的不同方式。這些方程式之所以被稱為“線性”,是因為所有變量的冪恰好是 1,且方程式的圖形解能形成一個平面。
線性方程組的一個常見案例是:在一個裝滿雞和兔的籠子里,如果你只知道所有雞和兔的頭有 10 個,腳有 30 只,那么這個倉庫里有多少只雞、多少只兔?這也是我們小學就熟悉的“雞兔同籠”問題。

由于很多時候雞和兔的數(shù)量并不多,我們也可以靠猜測試出答案,然后在老師收卷子的時候悄悄藏起草稿紙。
或許很多同學都在那時候心存僥幸,估計內心也以為這個問題并不難。直到有一天,大學線性代數(shù)課的老師拋出了這樣一個問題:
在諾亞方舟上船登記中,有1000種動物,所有動物有1023個頭,6566只腳,1254只角,25098顆牙齒,356對翅膀,3487對觸角,200萬億根毛發(fā)......(以上共1000種屬性),請問每種動物的數(shù)量。

才發(fā)現(xiàn),小學老師也是用心良苦,自己真是很傻很天真。好不容易頓悟之后,又在今天看著別人靠“猜測”發(fā)論文拿最佳論文獎,更是懷疑人生......

言歸正傳,線性方程組的應用當然遠遠不止于計算雞與兔乃至全世界所有動物的數(shù)量。它可以在許多實際場景中應用,比如建一條更堅固的橋梁,或造一架更隱蔽的飛機,這些工作可能都需要求解數(shù)百萬個相互依賴的線性方程組。
線性方程組是現(xiàn)代計算的主力軍。從根本上說,線性方程組是對許多計算機科學的問題進行優(yōu)化,這些問題主要是在約束系統(tǒng)內為一組變量尋找最佳值。如果我們可以更快地求解出線性方程組,那么我們也可以更快地解決這些計算機科學問題。
彭泱及其合作者所提出的新證明避開了以往求解方程組常用的矩陣乘法(matrix multiplication)。矩陣乘法限制了先前求解線性方程組的速度,因此,盡管如今矩陣乘法在求解線性方程組中仍發(fā)揮作用,但更多是扮演輔助的角色。彭泱等人將矩陣乘法與新的方法相結合,本質上是一種經過訓練的預測解答。
他們用于求解線性方程組的方法的計算步驟是n^2.332,而線性代數(shù)教科書中的經典方法的計算步驟是n^3。這個結果的意義有多大呢?假設要求解一個1000變量的線性方程組,或者說“諾亞方舟上的雞兔同籠問題”,經典方法需要10億步,而他們提出的方法只需要約1000萬步,只相當于前者的1%。隨著變量數(shù)的增加,其加速效果也越顯著。
籠子數(shù)學
回到前面所說的“籠子問題”。換個說法:假如農場里有雞、獨角犀牛和雙角山羊,通過快速計算,你確定有 12 個頭、38 只腳與 10 個角,請問每種動物分別有多少只?
在求解問題的過程中,為每只動物分配一個變量(c 代表雞,r 代表犀牛,g 代表山羊),并為每一個屬性(頭、腳、角)寫下一個方程式。每個變量前面的數(shù)字或系數(shù)代表了每只動物擁有的該屬性的數(shù)量。
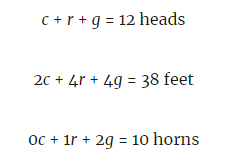
這時,我們得到了 3 個方程式與 3 個未知數(shù)。
求解這些問題的方法之一是變換一個方程式,并代入其它兩個方程式。例如,0c + 1r + 2g = 10 可以變?yōu)?r = 10 – 2g。然后,我們將 r 的值替換到其他兩個方程式中,以此類推,直到方程式里只包含一個變量,這時你就可以精確得到該變量的值。重復此過程,利用已解決的變量來得出其它變量即可。
除了上面這個方法,還有另外一種更復雜的求解方法,就是建立一個矩陣,矩陣的項(entry)為方程式的系數(shù)。上述的三個方程式可以轉變?yōu)槿缦戮仃嚕?/span>
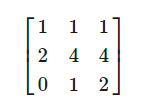
接下來,我們用另一個矩陣來表示數(shù)量未知的雞、犀牛和山羊。
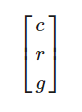
最后,我們用第三個矩陣來表示在倉庫里觀察到的頭、腳和角的數(shù)量。
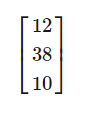
我們可以將這三個矩陣組合成一個簡單的線性方程組,其中,第一個矩陣乘以第二個矩陣的變量,等于第三個矩陣。這時,我們可以使用線性代數(shù)來求解第二個矩陣。
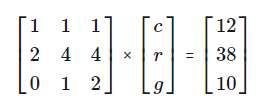
如果方程組有唯一解,我們可以利用克萊姆法則求出,這也是線性代數(shù)教材中必提的經典方法,它對于任意數(shù)量變量的線性方程式都適用。
無論是變換方程式(高斯消元法)還是采用矩陣方法,最終都將執(zhí)行相同數(shù)量的計算步驟來解決問題。也就是說,它們的計算步驟是相同的,即方程中變量數(shù)量的立方(n^3)。在上述方程中,有三個變量,因此需要27個計算步驟。如果有4種動物,則要求解它們需要64個步驟。如果有100種動物,則需要100萬個步驟。對于工程問題中數(shù)百萬變量的線性方程而言,其計算步驟更是天文數(shù)字。
在過去的50年中,研究人員一直致力于發(fā)現(xiàn)更有效地執(zhí)行此過程的方法。通常,他們可以采用一些捷徑(重用或合并操作的方式),從而可以用更少的步驟求解線性系統(tǒng)。
1969年,德國數(shù)學家 Volker Strassen 設計了一種僅以 n^2.81 個步驟來執(zhí)行矩陣乘法的算法。自此之后,數(shù)學家和計算機科學家開始爭相降低指數(shù)。來自麻省理工學院的副教授 Virginia Vassilevska Williams 和哈佛大學的博士后研究員 Josh Alman 于去年 10 月在這方面取得了最新進展,證明可以以 n^2.37286 個步驟執(zhí)行矩陣乘法,相比法國數(shù)學家 Le Gall 在 2014 年得到的結果(此前被認為是最好的結果)的指數(shù)下降了0.00001。
上述種種均表明:任何線性系統(tǒng)的求解都可以簡化為一個矩陣乘法的問題。
目前為止,在理論上,矩陣乘法至少可以以 n^2.37286 的步驟執(zhí)行。
但是,各種技術特征表明,求解線性系統(tǒng)的速度可能更快,也許只需要n^2步驟。我們使用矩陣乘法,是因為它是目前可用的最佳工具,但并不意味著不存在更好的工具。
據彭泱介紹:“如果你有一個裝滿計算機的房間,那么基于矩陣的算法便能夠順利地運算出有 50 個變量的方程組。現(xiàn)代數(shù)據的最大差異之一是該矩陣會變得非常大:不是 50x50,而是 10 億 x 10 億。大多項是以 0 開頭,因此,由于存儲限制,寫下密集的矩陣(例如逆矩陣)通常不可行。”
彭泱的合作者 Vempala 表示:“求解線性系統(tǒng)這一問題沒有理由要依賴于矩陣乘法的改進。”

圖注:Santosh Vempala是佐治亞理工學院的計算機科學杰出教授,主要研究領域是算法、隨機算法、計算幾何和計算學習理論。他曾獲得古根海姆獎、斯隆研究獎,并在2015年因“對凸集和概率分布算法的貢獻”入選ACM Fellow。
彭泱和 Vempala 證明了他們的算法能夠以 n^2.332 的計算步驟(計算復雜度)求解任何稀疏線性系統(tǒng)。這比矩陣乘法的最佳算法(n^2.37286)的指數(shù)快了四十分之一。對矩陣乘法進行漸進處理對于實際應用而言不會很快產生影響,但是作為一個概念證明,這種輕微的改進還是帶來了很明顯的進展:它表明存在一種求解線性系統(tǒng)的更好的方法。
Vempala 說:“從哲學上講,我們之前不知道是否可以比矩陣乘法更快,但現(xiàn)在我們知道了。”
還是以求解 1000 個變量的線性方程組為例,彭泱和 Vempala 的方法需要約 1000 萬步,Volker Strassen 的方法需要約 2 億 7 千萬步,Virginia Vassilevska Williams 和 Josh Alman的方法需要約1300萬步。
要了解新的改進工具,我們需要了解另一種求解線性系統(tǒng)的既定方法。這是一種直觀的方法,當遇到一群混淆在一起的雞、犀牛和山羊時:對每個物種猜一個數(shù),將它們插入等式中,看看離正確答案有多遠,然后再猜一次。
這種“迭代方法”是工程師和科學家經常采用的。它可以很好地解決許多實際問題,因為專家通常不會盲目猜測,從而減少了猜測的次數(shù)。彭泱說:“對于現(xiàn)實世界中的科學計算問題,人類對答案通常具有很好的直覺。”
迭代方法在直覺可以提供某些支持的特定情況下很有用。當嘗試求解的線性系統(tǒng)中包含大量系數(shù)為零的變量時,它們通常也會更有用。
在農場案例中,這種方法是很有用的。在此案例中,最容易直接求解的屬性是角。為什么?因為雞沒有角,從而將涉及三只動物的問題減少到實際上涉及兩只動物的問題。一旦擺脫了困境,就可以使用該信息快速求解腳和頭的問題。
在更復雜的線性系統(tǒng)中,這種關系(即并非所有屬性都與所有變量都有關)普遍存在。方程式可能有數(shù)百萬個變量和數(shù)百萬個方程式,但是每個方程式可能只涉及少量變量。這些類型的線性系統(tǒng)稱為“稀疏”,意味著大多數(shù)方程中大多數(shù)變量取零值。現(xiàn)實世界的線性系統(tǒng)中經常會出現(xiàn)這種情況。這是迭代方法可以擊敗矩陣乘法的關鍵。Williams說:“只有當矩陣足夠稀疏時,它才起作用。”

但是在進行這項新工作之前,沒有人設法證明對于所有稀疏線性系統(tǒng),迭代方法總是比矩陣乘法快。
協(xié)調隨機性
彭泱和Vempala的新技術采用了迭代猜測策略的增強版本:他們的算法不僅可以進行單次猜測,而且可以并行進行多個猜測。這種方法可以加快搜索速度,就像一眼看到很多人一樣。Giesbrecht說:“并行是魔法背后的秘密。”

論文地址:
一次進行多個猜測似乎是有用的,但是要使該策略起作用并不是那么簡單。
新算法的有效性在很大程度上取決于如何明智地進行引發(fā)迭代過程的初始猜測,以及尋找將并行猜測的結果組合成單個最終答案的巧妙方法。
回到農場的案例,該算法可能會首先進行三個初始猜測,其中每個猜測都是一個3×1矩陣,該矩陣指定了雞、犀牛和山羊的數(shù)量。該算法將觀察每個猜測和正確答案之間的差距,然后進行更多猜測,持續(xù)進行并行猜測線程。
該算法最終成功的關鍵在于,它會隨機進行三個初始猜測。隨機性可能對于猜測而言不是良好的起點,但作為一種通用方法,它具有獨特優(yōu)勢,尤其是在處理大量問題時。也就是說,隨機性可確保算法不會最終使搜索偏向問題的某一部分(從而有可能忽略實際解決方案所在的空間)。
彭泱說:“我需要確保所有的猜測都是足夠隨機的,以便它們涵蓋所有可能的組合。猜測是一種非常糟糕的方法,但隨著問題變得越來越大,它最終成為首選。”
在彭泱和Vempala的論文中,許多艱巨的技術工作都涉及證明隨機猜測的不同部分也可以協(xié)同工作,包括實際上是最終答案的任何特定猜測。“存在協(xié)調的隨機性,” Vempala說。
這意味著隨機猜測不僅可以包含猜測本身的確切值,還可以涵蓋介于兩者之間的所有潛在猜測。這類似于兩個人在森林中搜尋并不僅僅是搜尋他們所走的地面,還覆蓋了他們視野內的區(qū)域。Vempala說:“兩個 [猜測] 之間的所有內容也都包括在內。”
此搜索功能可確保算法將在某處找到答案,但是它本身并不能識別答案。為此,彭泱和Vempala必須做額外的證明。
該算法將隨機猜測作為矩陣中的條目進行追蹤。在矩陣條目中尋找答案使問題變成了矩陣乘法的問題,這當然是他們要規(guī)避的障礙。但是在這里,他們再次利用了隨機性。
因為矩陣中的條目是隨機的,并且它們之間發(fā)生協(xié)調,所以矩陣本身最終會具有某些對稱性。這些對稱性使快捷計算快捷成為可能。就像任何高度對稱的對象一樣,只需要知道其一部分,就可以推斷出整體。
結果,彭泱和Vempala的算法可以比沒有對稱性的矩陣更快地在矩陣中找到解。矩陣的對稱性也傳達了另一個重要的好處:有助于確保猜測永遠不會太大(導致以算法效率的角度來看變得難以理解)。彭泱說:“在進行猜測和協(xié)調時,我們必須控制數(shù)字的大小。”
參考鏈接:
https://www.quantamagazine.org/new-algorithm-breaks-speed-limit-for-solving-linear-equations-20210308/ http://www.chinaqw.com/node2/node2796/node2882/node3156/userobject6ai253919.html https://www.cc.gatech.edu/news/642724/linear-systems-research-wins-soda-best-paper-award https://www.cc.gatech.edu/~rpeng/