基于OpenCV的位姿估計

點擊上方“小白學視覺”，選擇加"星標"或“置頂”

重磅干貨，第一時間送達

今天我們的目標是找出我們相對于球場上的位置，從而了解我們在比賽中的全局位置。

單應性是一種平面關系，可將點從一個平面轉換為另一個平面。它是一個3乘3的矩陣，轉換3維矢量表示平面上的2D點。這些向量稱為同質坐標，下面將進行討論。下圖說明了這種關系。這四個點在紅色平面和圖像平面之間相對應。單應性存儲相機的位置和方向，這可以通過分解單應性矩陣來檢索。

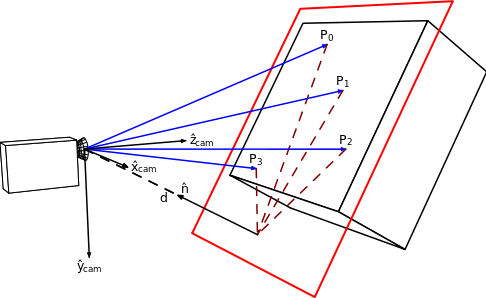
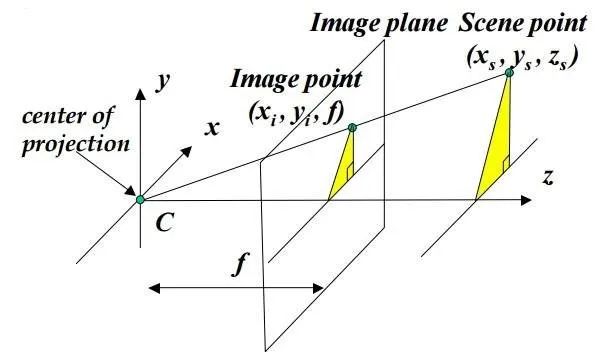
針孔相機

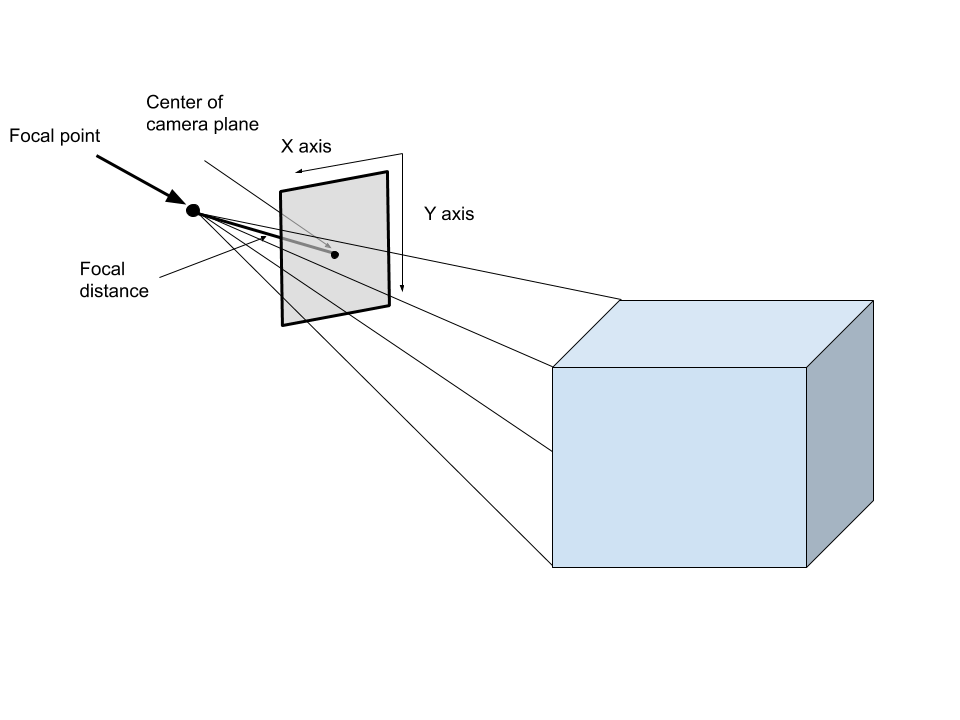
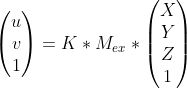
針孔相機數(shù)學模型

針孔相機模型是相機的數(shù)學表示。它接受3D點并將其投影到像上圖所示的圖像平面上。該模型的重要方面是焦點，像平面（上圖中的灰度平面），主點（上圖中的像面上的粗體點），焦距（像平面與像之間的距離）焦點）和光軸（垂直于穿過焦點的像平面的線）。可以在投影矩陣中編碼該變換，該投影矩陣將表示3D點的4維均勻向量轉換為表示圖像平面上2d點的3維均勻向量。

齊次坐標是表示計算機視覺中的點的投影坐標。由于拍攝照片時會從3D轉換為2D，因此深度范圍會丟失。因此，可以將無限數(shù)量的3D點投影到相同的2D點，這使得同質坐標在描述可能性射線時非常通用，因為它們的比例相似。齊次坐標僅取直角坐標，并將維數(shù)增大到末端。

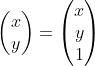
用齊次坐標表示的笛卡爾坐標，在比例上也相等。

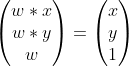
請注意，三角形可能會越來越遠且更大，但仍然可以產生相同的圖像給定同質坐標，將所有元素除以矢量的最后一個元素（比例因子），然后笛卡爾坐標是一個矢量，該矢量由除最后一個元素之外的所有元素組成。

投影矩陣是與相機屬性相關的其他兩個矩陣的乘積。它們是外部和內部相機矩陣。這些矩陣分別存儲攝像機的外部參數(shù)和固有參數(shù)（因此命名）。

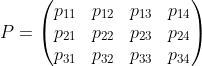
投影矩陣（3 x 4矩陣）

外參矩陣

外在矩陣存儲攝像機在全局空間中的位置。該信息存儲在旋轉矩陣以及平移矢量中。旋轉矩陣存儲相機的3D方向，而平移矢量將其位置存儲在3D空間中。

旋轉矩陣

然后將旋轉矩陣和平移向量連接起來以創(chuàng)建外部矩陣。從功能上講，外部矩陣將3D同類坐標從全局坐標系轉換為相機坐標系。因此，所有變換后的矢量將相對于焦點在空間中表示相同的位置。

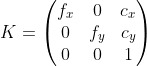
內參矩陣

本征矩陣存儲相機的本征，例如焦距和主點。焦距（f 1和f 6）是從焦點到像面的距離，可以用像素寬度或像素高度（因此為何有2個焦距）來度量。每個像素都不是一個完美的正方形，因此每個邊都有不同的邊長。主點（c?和c?）是光軸和像平面（像平面的功能中心）的交點。該矩陣將相對于焦點的3D坐標轉換到圖像平面上；將其視為拍攝照片的矩陣。當與外部矩陣組合時，將創(chuàng)建針孔相機模型。

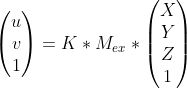
針孔相機數(shù)學模型

現(xiàn)在，單應性是針孔相機模型的特殊情況，其中投影到相機上的所有現(xiàn)實世界坐標都位于z坐標為0的平面上。

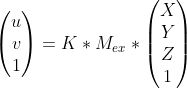
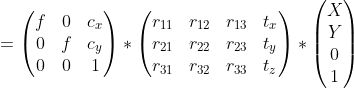
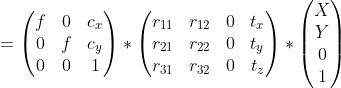
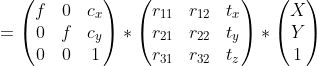
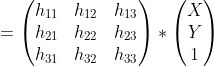
H是單應性矩陣，是3 x 3矩陣，可將點從一個平面轉換為另一個平面。在這里，變換是在Z = 0的平面和指向該點的圖像平面之間進行的投影。單應性矩陣通常通過4點算法求解。本質上，它使用來自2個平面的4個點對應來求解單應矩陣。在OpenCV中，我們可以使用cv2.findHomography方法找到單應矩陣：

cv2.findHomography(, )

此方法需要某種形式的特征點跟蹤，以便上面方法的結果。坐標測量的質量將有助于上述方法的準確性。一旦有了單應性矩陣，就可以將其分解為攝像機的平移和旋轉。單應矩陣的分解如下所示：

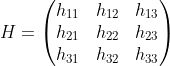
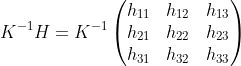
我們可以通過將解決方案矩陣的前兩列用作旋轉矩陣中的前兩列，然后使用叉積來找到旋轉矩陣的最后一列，從而得出旋轉矩陣。翻譯是解決方案矩陣的最后一列。

'''H is the homography matrixK is the camera calibration matrixT is translationR is rotation'''H = H.Th1 = H[0]h2 = H[1]h3 = H[2]K_inv = np.linalg.inv(K)L = 1 / np.linalg.norm(np.dot(K_inv, h1))r1 = L * np.dot(K_inv, h1)r2 = L * np.dot(K_inv, h2)r3 = np.cross(r1, r2)T = L * (K_inv @ h3.reshape(3, 1))R = np.array([[r1], [r2], [r3]])R = np.reshape(R, (3, 3))

代碼鏈接：https://github.com/RaubCamaioni/OpenCV_Position

使用Homography比其他算法簡單得多，因為它非常簡單直觀。利用基本或基本矩陣的其他方法需要復雜的算法和更多的實現(xiàn)精力。由于所有視覺本地化方法都在做相同的事情，因此最好在可能的情況下使用Homography，以節(jié)省時間和精力。

交流群

歡迎加入公眾號讀者群一起和同行交流，目前有SLAM、三維視覺、傳感器、自動駕駛、計算攝影、檢測、分割、識別、醫(yī)學影像、GAN、算法競賽等微信群（以后會逐漸細分），請掃描下面微信號加群，備注：”昵稱+學校/公司+研究方向“，例如：”張三?+?上海交大?+?視覺SLAM“。請按照格式備注，否則不予通過。添加成功后會根據(jù)研究方向邀請進入相關微信群。請勿在群內發(fā)送廣告，否則會請出群，謝謝理解~