請問二叉樹等數(shù)據(jù)結(jié)構(gòu)的物理存儲結(jié)構(gòu)是怎樣的?
請問二叉樹等數(shù)據(jù)結(jié)構(gòu)的物理存儲結(jié)構(gòu)是怎樣的?
好吧,咱們書上說了,一般兩種存儲方式: 1. 以完全二叉樹的形式用連續(xù)空間的數(shù)組存儲; 2. 以鏈表形式存儲,即各個數(shù)據(jù)之間保存了相關(guān)的數(shù)據(jù)的指針地址!
如果回答就是這樣,那么我想大家也不費那神了,直接洗洗睡吧?咱們能不能深入點?
數(shù)組是好理解的,在內(nèi)存在磁盤都是一樣的,連續(xù)相鄰的空間,挨著存放到磁盤就可以了;好吧,就算你正確?那么鏈表呢?拿簡單的單鏈表來說,上一個節(jié)點保存下一個節(jié)點的指針?是如何保存的?我們能想到的,就是一個上一節(jié)點存儲了下一節(jié)點的絕對地址或者偏移地址,好像是這樣的!
那么問題來了,這個下一節(jié)點地址到底是什么樣的呢?是相對地址還是絕對地址?這個地址是怎么算出來的?存儲在內(nèi)存上是肯定沒有問題的!但是如果存儲在磁盤上呢?如果這個地址是固定的,那么,如果換了硬盤(換了存儲介質(zhì)),是否就找不到該地址(因為每個設(shè)備的地址自然是不一樣的)?
針對這個問題,很是困擾了我很久!也詢問過幾個身邊的小伙伴,也都說不知道。后來在一次面試中,一面試官剛好問我這問題,我把自己的見解說完后,說我確實不知道是怎么存儲的。最后我要求他給予答案,然后,他說,就是存儲的下一節(jié)點的地址(內(nèi)存地址),壓根不存在什么數(shù)據(jù)結(jié)構(gòu)存儲于磁盤這種說法,內(nèi)存中,是動態(tài)計算的值。如果存在內(nèi)存拷貝,那么,也會重新計算這些地址的,所以看起來相同的結(jié)構(gòu),在不同存儲工具上,會會表現(xiàn)出不同的地址空間。
好吧,我將信將疑!被丟了n個鄙視的表情,然后被pass掉了。
那么,到底內(nèi)存中的二叉樹怎么存儲在硬盤上的呢?
其實硬盤上并沒有什么二叉樹的,硬盤只是充當(dāng)了一個存儲介質(zhì),只是提供你要讀的時候可以取而已,而真正的數(shù)據(jù)結(jié)構(gòu),則需要在用的時候再還原出原來的樹形結(jié)構(gòu)!
下面以一個簡單的示例來展示磁盤上的數(shù)據(jù)結(jié)構(gòu)的存儲方式:
public class BinTreeDiskSample {private static int h = -1;private static Node root;static class Node implements Serializable {private static final long serialVersionUID = -4780741633734920991L;int data;transient Node left;transient Node right;int lHeight = -1, rHeight = -1;public Node(int data) {this.data = data;}public Node setLeft(Node left) {this.left = left;return this;}public Node setRight(Node right) {this.right = right;return this;}public Node getLeft() {return left;}public Node getRight() {return right;}// 后續(xù)遍歷寫入,先序遍歷讀出public int write(ObjectOutputStream out) throws IOException {if (left != null) {lHeight = left.write(out);}if (right != null) {rHeight = right.write(out);}h++;out.writeObject(this);return h;}private void init(List<Node> list) {if (lHeight != -1) {left = list.get(lHeight);left.init(list);}if (rHeight != -1) {right = list.get(rHeight);right.init(list);}}}public static void binTreePreOrderPrint(Node root) {System.out.print(root.data + " "); // visit rootif(root.left != null) {binTreePreOrderPrint(root.left);}if(root.right != null) {binTreePreOrderPrint(root.right);}}// 先序遍歷讀出public static void read(ObjectInputStream in) throws IOException,ClassNotFoundException {List<Node> list = new ArrayList<Node>();Node n;Object obj;try {while ((obj = in.readObject()) != null) {n = (Node) obj;list.add(n);}}catch (Exception e) {// EOFException ...// e.printStackTrace();}root = list.get(list.size() - 1);root.init(list);}public static void main(String args[]) throws FileNotFoundException,IOException, ClassNotFoundException {// 構(gòu)造一棵二叉樹 11 21 41 61 51 31Node n6 = new Node(61);Node n4 = new Node(41).setLeft(n6);Node n5 = new Node(51);Node n2 = new Node(21).setLeft(n4).setRight(n5);Node n3 = new Node(31);Node n1 = new Node(11).setLeft(n2).setRight(n3);root = n1;System.out.println("output node: ");binTreePreOrderPrint(root);// 將數(shù)據(jù)寫稿磁盤ObjectOutputStream out = new ObjectOutputStream(new FileOutputStream("btree.bin"));root.write(out);out.close();root = null;// 將數(shù)據(jù)從磁盤讀入,并進行數(shù)據(jù)結(jié)構(gòu)的重新構(gòu)建ObjectInputStream in = new ObjectInputStream(new FileInputStream("btree.bin"));read(in);in.close();System.out.println("\nread node: ");binTreePreOrderPrint(root);}}
輸出:
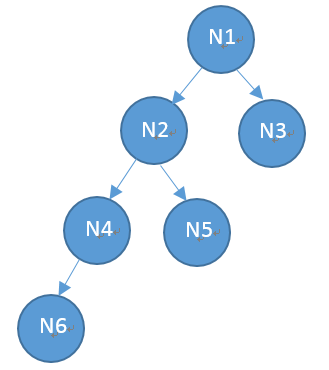
如上二叉樹的磁盤存儲,使用了java自帶的序列化工具,將節(jié)點寫入磁盤(注:這并不是一種好的實踐),然后在讀出的時候,按照寫稿時候的規(guī)則,進行重新構(gòu)建二叉樹即可。
所以:
存儲磁盤的數(shù)據(jù)結(jié)構(gòu),只是一種約定的方式,只是為了方便在重新恢復(fù)鏈表,二叉樹等等內(nèi)存結(jié)構(gòu)的算法而已。
如:數(shù)據(jù)庫索引是存儲在磁盤上,當(dāng)表中的數(shù)據(jù)量比較大時,索引的大小也跟著增長,達到幾個G甚至更多。當(dāng)我們利用索引進行查詢的時候,不可能把索引全部加載到內(nèi)存中,只能逐一加載每個磁盤頁,這里的磁盤頁就對應(yīng)索引樹的節(jié)點。
B+/-樹索引用使用很多的數(shù)據(jù)結(jié)構(gòu),下面做一點簡單介紹:
一、B-Tree
m階B-Tree滿足以下條件:
1、每個節(jié)點最多擁有m個子樹
2、根節(jié)點至少有2個子樹
3、分支節(jié)點至少擁有m/2顆子樹(除根節(jié)點和葉子節(jié)點外都是分支節(jié)點)
4、所有葉子節(jié)點都在同一層、每個節(jié)點最多可以有m-1個key,并且以升序排列
二、B+Tree的定義
B+Tree是B樹的變種,有著比B樹更高的查詢性能,來看下m階B+Tree特征:
1、有m個子樹的節(jié)點包含有m個元素(B-Tree中是m-1)
2、根節(jié)點和分支節(jié)點中不保存數(shù)據(jù),只用于索引,所有數(shù)據(jù)都保存在葉子節(jié)點中。
3、所有分支節(jié)點和根節(jié)點都同時存在于子節(jié)點中,在子節(jié)點元素中是最大或者最小的元素。
4、葉子節(jié)點會包含所有的關(guān)鍵字,以及指向數(shù)據(jù)記錄的指針,并且葉子節(jié)點本身是根據(jù)關(guān)鍵字的大小從小到大順序鏈接。
下面讓我們來看看現(xiàn)代數(shù)據(jù)庫的磁盤存儲結(jié)構(gòu)吧:
以下部分內(nèi)容摘自:https://blog.csdn.net/qq910894904/article/details/39312901
我們都知道,數(shù)據(jù)庫通常使用B+樹作為索引,但是國內(nèi)很少有人提到數(shù)據(jù)庫使用的是HeapFile來管理記錄的存儲。國外的一些大學(xué)在“數(shù)據(jù)庫系統(tǒng)實現(xiàn)”這門課上通常會讓學(xué)生實現(xiàn)一個簡單的數(shù)據(jù)庫,因此有不少HeapFile的資料。
基于Page的HeapFile
采用鏈表形式的是HeapFile如下:
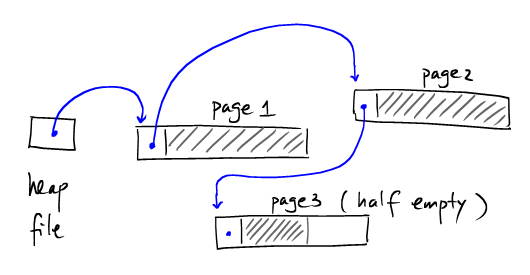
Heap file和鏈表結(jié)構(gòu)類似的地方:
支持增加(append)功能
支持大規(guī)模順序掃描
不支持隨機訪問
這種方式的HeapFile在尋找具有合適空間的半空Page時需要遍歷多個頁,I/O開銷大。因此一般常用的是采用基于索引的HeaFile.在HeapFile中使用一部分空間來存儲Page作為索引,并記錄對應(yīng)Page的剩余量。如下:
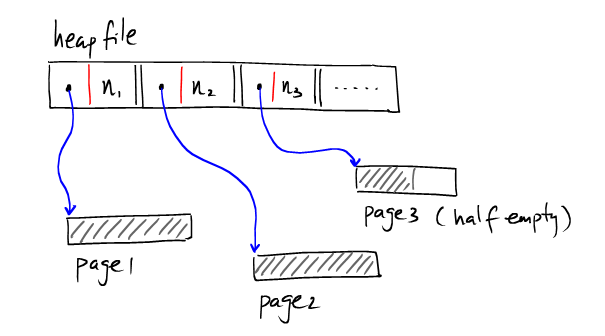
像上圖那樣,索引單獨存在一個page上。數(shù)據(jù)記錄存在其他page上,如果有多個索引的page,則可以表示為:
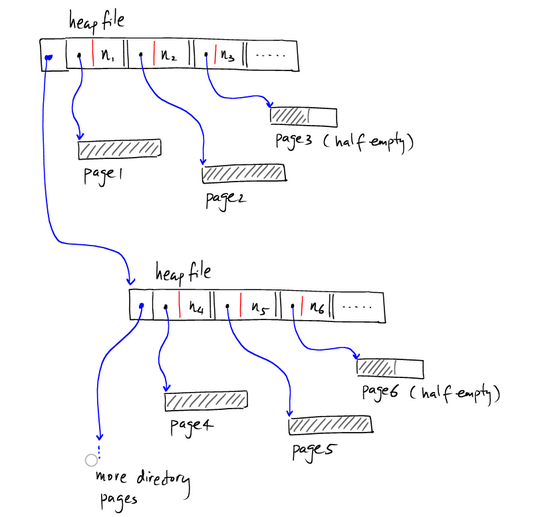
下面是Heap file自有的一些特性:
數(shù)據(jù)保存在二級存儲體(disk)中:Heapfile主要被設(shè)計用來高效存儲大數(shù)據(jù)量,數(shù)據(jù)量的大小只受存儲體容量限制;
Heapfile可以跨越多個磁盤空間或機器:heapfile可以用大地址結(jié)構(gòu)去標(biāo)識多個磁盤,甚至于多個網(wǎng)絡(luò);
數(shù)據(jù)被組織成頁;
頁可以部分為空(并不要求每個page必須裝滿);
頁面可以被分割在某個存儲體的不同的物理區(qū)域,也可以分布在不同的存儲體上,甚至是不同的網(wǎng)絡(luò)節(jié)點中。我們可以簡單假設(shè)每一個page都有一個唯一的地址標(biāo)識符PageAddress,并且操作系統(tǒng)可以根據(jù)PageAddress為我們定位該Page。
一般情況下,使用page在其所在文件中的偏移量就可以表示了。

騰訊、阿里、滴滴后臺面試題匯總總結(jié) — (含答案)
面試:史上最全多線程面試題 !
最新阿里內(nèi)推Java后端面試題
JVM難學(xué)?那是因為你沒認真看完這篇文章

關(guān)注作者微信公眾號 —《JAVA爛豬皮》
了解更多java后端架構(gòu)知識以及最新面試寶典

看完本文記得給作者點贊+在看哦~~~大家的支持,是作者源源不斷出文的動力
作者:等你歸去來
出處:https://www.cnblogs.com/yougewe/p/9901758.html
